人教版七年级下册数学学案:5.2.2平行线的判定1
文档属性
| 名称 | 人教版七年级下册数学学案:5.2.2平行线的判定1 |
|
|
| 格式 | zip | ||
| 文件大小 | 37.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 00:00:00 | ||
图片预览

文档简介
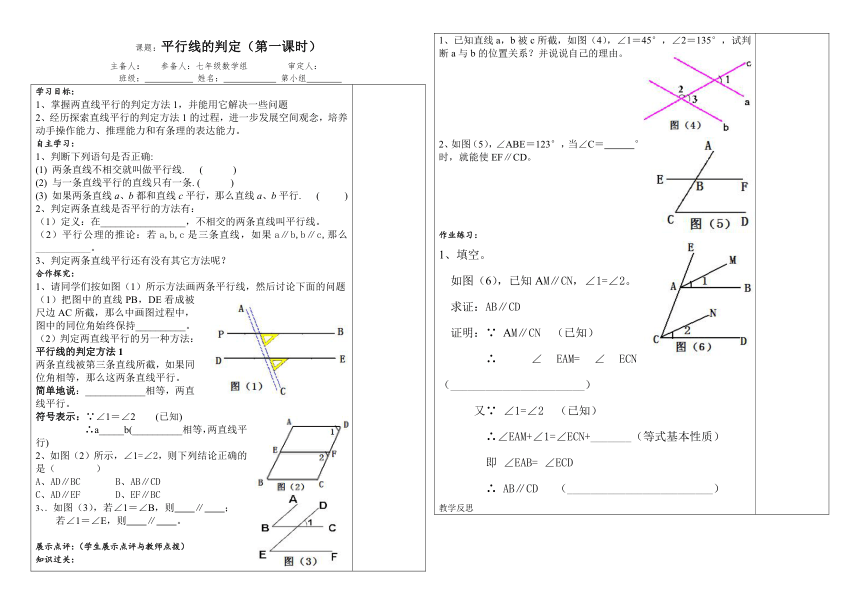
课题:平行线的判定(第一课时)
主备人:
参备人:七年级数学组
审定人:
班级:
姓名:
第小组
学习目标:
1、掌握两直线平行的判定方法1,并能用它解决一些问题
2、经历探索直线平行的判定方法1的过程,进一步发展空间观念,培养动手操作能力、推理能力和有条理的表达能力。
自主学习:
1、判断下列语句是否正确:
(1)
两条直线不相交就叫做平行线.
(
)
(2)
与一条直线平行的直线只有一条.
(
)
(3)
如果两条直线a、b都和直线c平行,那么直线a、b平行.
(
)
2、判定两条直线是否平行的方法有:
(1)定义:在_________________,不相交的两条直线叫平行线。
(2)平行公理的推论:若a,b,c是三条直线,如果a∥b,b∥c,那么___________。
3、判定两条直线平行还有没有其它方法呢?
合作探究:
1、请同学们按如图(1)所示方法画两条平行线,然后讨论下面的问题
(1)把图中的直线PB,DE看成被尺边AC所截,那么中画图过程中,图中的同位角始终保持__________。
(2)判定两直线平行的另一种方法:
平行线的判定方法1
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单地说:____________相等,两直线平行。
符号表示:∵∠1=∠2
(已知)
∴a_____b(__________相等,两直线平行)
2、如图(2)所示,∠1=∠2,则下列结论正确的是(
)
A、AD∥BC
B、AB∥CD
C、AD∥EF
D、EF∥BC
3、.如图(3),若∠1=∠B,则 ∥ ;
若∠1=∠E,则 ∥ 。
展示点评:(学生展示点评与教师点拨)
知识过关:
1、已知直线a,b被c所截,如图(4),∠1=45°,∠2=135°,试判断a与b的位置关系?并说说自己的理由。
2、如图(5),∠ABE=123°,当∠C=
°时,就能使EF∥CD。
作业练习:
1、填空。
如图(6),已知AM∥CN,∠1=∠2。
求证:AB∥CD
证明:∵
AM∥CN
(已知)
∴
∠EAM=∠ECN
(_______________________)
又∵
∠1=∠2
(已知)
∴∠EAM+∠1=∠ECN+_______(等式基本性质)
即
∠EAB=
∠ECD
∴
AB∥CD
(_________________________)
教学反思
主备人:
参备人:七年级数学组
审定人:
班级:
姓名:
第小组
学习目标:
1、掌握两直线平行的判定方法1,并能用它解决一些问题
2、经历探索直线平行的判定方法1的过程,进一步发展空间观念,培养动手操作能力、推理能力和有条理的表达能力。
自主学习:
1、判断下列语句是否正确:
(1)
两条直线不相交就叫做平行线.
(
)
(2)
与一条直线平行的直线只有一条.
(
)
(3)
如果两条直线a、b都和直线c平行,那么直线a、b平行.
(
)
2、判定两条直线是否平行的方法有:
(1)定义:在_________________,不相交的两条直线叫平行线。
(2)平行公理的推论:若a,b,c是三条直线,如果a∥b,b∥c,那么___________。
3、判定两条直线平行还有没有其它方法呢?
合作探究:
1、请同学们按如图(1)所示方法画两条平行线,然后讨论下面的问题
(1)把图中的直线PB,DE看成被尺边AC所截,那么中画图过程中,图中的同位角始终保持__________。
(2)判定两直线平行的另一种方法:
平行线的判定方法1
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单地说:____________相等,两直线平行。
符号表示:∵∠1=∠2
(已知)
∴a_____b(__________相等,两直线平行)
2、如图(2)所示,∠1=∠2,则下列结论正确的是(
)
A、AD∥BC
B、AB∥CD
C、AD∥EF
D、EF∥BC
3、.如图(3),若∠1=∠B,则 ∥ ;
若∠1=∠E,则 ∥ 。
展示点评:(学生展示点评与教师点拨)
知识过关:
1、已知直线a,b被c所截,如图(4),∠1=45°,∠2=135°,试判断a与b的位置关系?并说说自己的理由。
2、如图(5),∠ABE=123°,当∠C=
°时,就能使EF∥CD。
作业练习:
1、填空。
如图(6),已知AM∥CN,∠1=∠2。
求证:AB∥CD
证明:∵
AM∥CN
(已知)
∴
∠EAM=∠ECN
(_______________________)
又∵
∠1=∠2
(已知)
∴∠EAM+∠1=∠ECN+_______(等式基本性质)
即
∠EAB=
∠ECD
∴
AB∥CD
(_________________________)
教学反思
