3.2波的描述—【新教材】人教版高中物理选择性必修第一册同步检测
文档属性
| 名称 | 3.2波的描述—【新教材】人教版高中物理选择性必修第一册同步检测 |
|
|
| 格式 | docx | ||
| 文件大小 | 382.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-02-02 00:00:00 | ||
图片预览




文档简介
3.2播的描述
一、单选题
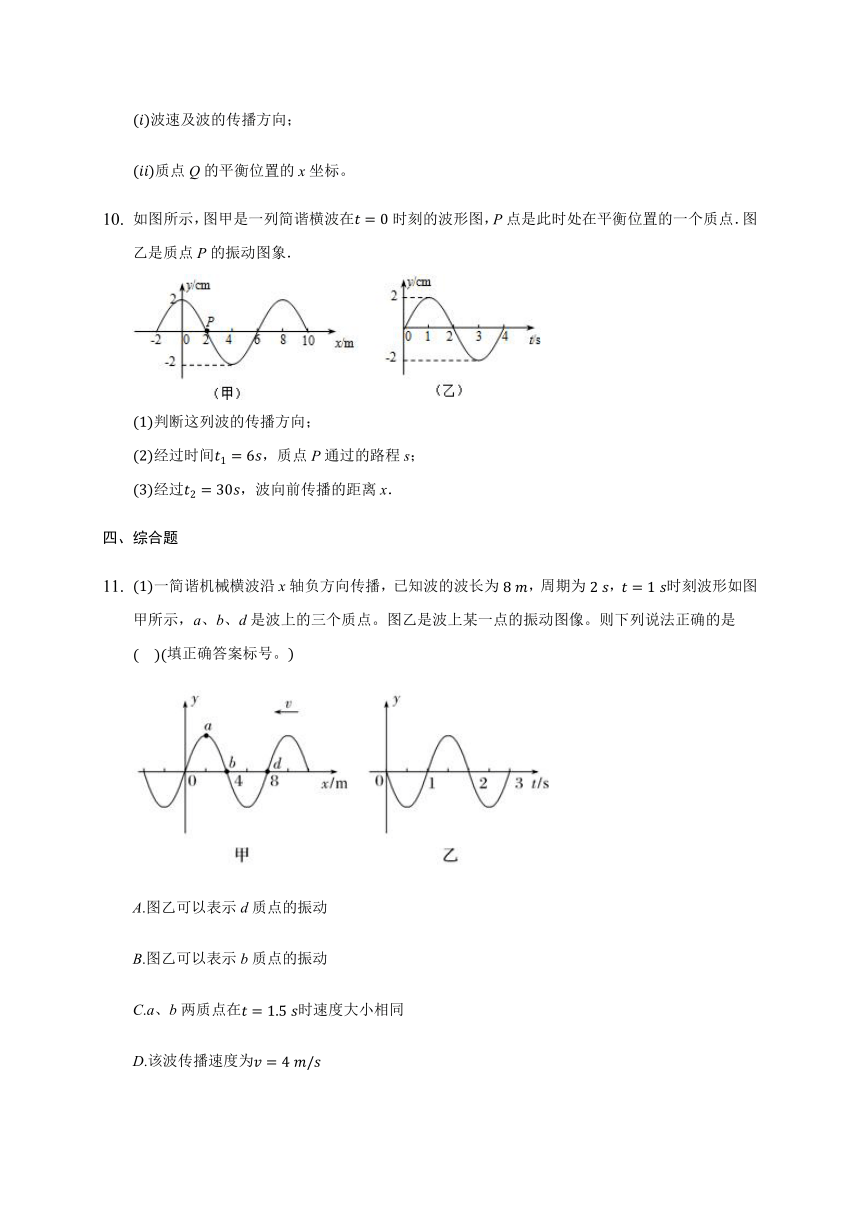
一列简谐横波在某一时刻的波形图如图中实线所示,经0.2?s后,其波形如图中虚线所示。则该简谐波的波速不可能是(?)
A. 2.1?m/s B. 3.9?m/s C. 7.2?m/s D. 14.1?m/s
一列简谐横波沿x轴传播,图甲是t=1.0s时的波形图,图乙是x=3.0m处质点的振动图像,a、b质点在x轴上平衡位置分别为xa=0.5m、xb=2.5m,下列说法正确的是
A. 波沿x轴正方向传播
B. 波的传播速度为0.5?m/s
C. t=1.5?s时,a、b两点的速度和加速度均等大反向
D. 从t=1.0?s到t=1.5?s质点a的路程为10?cm
如图所示分别为一列横波在某一时刻的图像和在x=6m处的质点从该时刻开始计时的振动图像,则这列波(????)
A. 沿x轴的正方向传播
B. 波速为100m/s
C. 该质点振动周期为8s
D. 再过0.04s,x=4m处的质点在平衡位置且向上运动
一列简谐横波在某一时刻的波形图如图中实线所示,经0.2?s后,其波形如图中虚线所示。则该简谐波的波速不可能是(? ? )
A. 2.1?m/s B. 3.9?m/s C. 7.2?m/s D. 14.1?m/s
二、多选题
一列简谐横波沿x轴传播,t=0和t=0.20s时的波形分别如图中实线和虚线所示。已知t=0.20s时,x=2cm位置的质点处于平衡位置,该波的周期T>0.30s。下列说法正确的是(????)
A. 该波的周期T=1.6s
B. 该波沿x轴正方向传播,波速为0.7m/s
C. x=0位置的质点在t=0.4s时处于平衡位置
D. x=16cm位置的质点在t=0.12s时处于波谷
如图所示,一列简谐横波沿x轴正方向传播,在t1=0时刻波传播到x=2?m处的质点C,此时x=0.5?m处的质点A在负方向最大位移处,在t2=0.3?s时刻质点A处于平衡位置且向下振动,则下列判断正确的是
A. 该简谐横波的波速可能等于5 m/s
B. 质点C开始振动时的运动方向沿y轴负方向
C. 在t1~t2时间内,x=1 m处的质点B通过的路程可能大于6.0 cm
D. 在t2时刻,位于x=3 m处的质点D处于负方向最大位移处
如图,a、b、c、d是均匀媒质x轴上的四个质点,相邻两点的间距依次为4?m、8?m和16?m。一列简谐横波以4?m/s的波速沿x轴正向传播,在t=?10?s时刻到达质点c处,质点c由平衡位置开始垂直x轴向上运动,t=?13?s时c第一次到达最低点。则
A. 在t=?7s时刻质点a垂直x轴向上运动
B. 在t=?9s时刻质点b恰好到达最高点
C. 在t=?15s时刻a、d之间有两个波谷
D. 在15?s?三、计算题
一列简谐横波图象如下图所示,t1时刻的波形如图中实线所示,t2时刻的波形如图中虚线所示,已知Δt=t2-t1=0.5s,问:
(1)这列波的可能波速的表达式?
(2)若波向左传播,且3T<Δt<4T,波速多大?
(3)若波速ν=68m/s,则波向哪个方向传播?
如图是某横波的波形图,实线表示某时刻的波形,虚线表示0.2s后的波形图.
(1)若波向左传播,则它传播的可能距离是多少?
(2)若波向右传播,则它的最大周期是多少?
(3)若波速为35m/s,则波的传播方向如何?
一列简谐横波在t=13s的波形图如图(a)所示,P、Q是介质中的两个质点,图(b)是质点Q的振动图象。求:
(i)波速及波的传播方向;
(ii)质点Q的平衡位置的x坐标。
如图所示,图甲是一列简谐横波在t=0时刻的波形图,P点是此时处在平衡位置的一个质点.图乙是质点P的振动图象.
(1)判断这列波的传播方向;
(2)经过时间t1=6s,质点P通过的路程s;
(3)经过t2=30s,波向前传播的距离x.
四、综合题
(1)一简谐机械横波沿x轴负方向传播,已知波的波长为8?m,周期为2?s,t=1?s时刻波形如图甲所示,a、b、d是波上的三个质点。图乙是波上某一点的振动图像。则下列说法正确的是(????)(填正确答案标号。)
A.图乙可以表示d质点的振动
B.图乙可以表示b质点的振动
C.a、b两质点在t=1.5?s时速度大小相同
D.该波传播速度为v=4?m/s
E.t=0时b质点速度沿y轴正方向
(2)如图中实线是一列简谐横波在t1=0时刻的波形,虚线是这列波在t2=0.5?s时刻的波形。
(1)写出这列波的波速表达式;
(2)若波速大小为74?m/s,波速方向如何?
(1)图(a)为一列简谐横波在t=2s时的波形图,图(b)为介质中平衡位置在x=2.5m处的质点的振动图象,P是平衡位置为x=1m的质点,下列说法正确的是_________.
A.波速为0.5m/s
B.波的传播方向向左
C.0~1.5s,P运动的路程为6cm
D.3s~5s,P振动方向发生变化
E.t=9s时,P的加速度恰好为零
(2)如图所示,直角玻璃三棱镜置于空气中,已知∠A=60°,∠C=90°,一束极细的光于AC的中点D垂直AC面入射,棱镜的折射率为n=2。
①求此玻璃对空气的临界角;
②光从棱镜第一次射入空气时的折射角。
(1)如图为一列传播速率v=8m/s的简谐横波在t=0时刻的波形图,P是平衡位置为x1=3.5m处的质点,Q是平衡位置为x2=26m处的质点,此时质点P正做减速运动,则(????)
A. 该波沿x轴负方向传播
B.t=2.5s时,Q质点开始振动
C.Q质点的起振方向沿y轴正向
D.t=2.7s时质点Q向y轴正方向加速运动
E.?1s内质点P通过的路程为40 cm
(2)如图所示,小玻璃球的半径为R,折射率n=3,今有一束细光束从与直径相距d=32R的点,沿直径方向照在小玻璃球上,入射光线可经过折射、反射、折射,再射出后恰能平行于原射入方向返回。已知光在真空中的传播速度为c,求该细光束在玻璃球中的传播时间。
而可求出时间。本题考查了折射定律的应用,正确作出光路图,灵活运用几何知识求解是关键。
(1)一列简谐横波在同种均匀介质中传播,某时刻波形如图甲所示。由该时刻开始计时,质点L的振动情况如图乙所示。下列说法正确的是(????)
A.该横波沿x轴正方向传播
B.质点N该时刻向y轴正方向运动
C.质点L经半个周期将沿x轴正方向移动
D.该时刻质点K与M的速度、加速度大小都相同
E.从该时刻起,质点O与质点N的振动情况始终相同
(2)如图所示,圆心为O、半径为R的半圆形玻璃砖置于水平面上,当入射角为θ时,光线从玻璃砖P点射入后,直接从圆形表面顶端B点射出,已知OP=2R2,sinθ=63,真空中的光速为c.求:
Ⅰ.玻璃砖的折射率n;
Ⅱ.当光线垂直OP边从P点入射时,光在玻璃中传播所用的时间t。
3.2播的描述
一、单选题
一列简谐横波在某一时刻的波形图如图中实线所示,经0.2?s后,其波形如图中虚线所示。则该简谐波的波速不可能是(?)
center0A. 2.1?m/s B. 3.9?m/s C. 7.2?m/s D. 14.1?m/s
【答案】C
【解析】
【分析】
本题是波动图象中典型的问题,要根据波的周期性和双向性研究时间与周期的关系,熟练运用波形平移法研究。由图可知波的波长,而由两列波的波形图可得两波形相距的时间与周期的关系,则可得出波速的表达式。
【解答】
由图可知,波的波长为0.24m,如果波向右传播,0.2=(n+34)T,得到波速v=λT=(1.2n+0.90)m/s,(n=0,1,2,3...),当n=1时,v=2.1m/s,当n=11时,v=14.1m/s;
如果波向左传播,0.2=(n+14)T,得到波速v=λT=(1.2n+0.3)m/s,(n=0,1,2,3...)当n=3时,v=3.9m/s,故ABD正确,C错误。
故选C。
一列简谐横波沿x轴传播,图甲是t=1.0s时的波形图,图乙是x=3.0m处质点的振动图像,a、b质点在x轴上平衡位置分别为xa=0.5m、xb=2.5m,下列说法正确的是
center0A. 波沿x轴正方向传播
B. 波的传播速度为0.5?m/s
C. t=1.5?s时,a、b两点的速度和加速度均等大反向
D. 从t=1.0?s到t=1.5?s质点a的路程为10?cm
【答案】C
【解析】
【分析】
本题考查波的图像和振动图像,关键是能够从图像中分析出波的传播信息和质点的振动信息,基础题。
根据图像结合“上坡下,下坡上”的规律分析波的传播方向;根据波长、波速和周期关系计算波速;根据平移法分析a、b质点振动情况及路程。
【解答】,
A.t=1s时,x=3.0m处质点向y轴正方向振动,根据“上坡下,下坡上”可知波沿x轴负方向传播,故A错误;
B.根据图像可知该波波长λ=4m,周期T=2s,故波的传播速度为v=λT=2m/s,故B错误;
C.根据波的平移,可知t=1.5s时,a质点在y=-52cm位置向y轴负方向振动,b质点在y=52cm位置向y轴正方向振动,故a、b两点的速度和加速度均等大反向,故C正确;
D.从t=1.0s到t=1.5s质点a的路程为102cm,故D错误。
故选C。
如图所示分别为一列横波在某一时刻的图像和在x=6m处的质点从该时刻开始计时的振动图像,则这列波(????)
center0A. 沿x轴的正方向传播
B. 波速为100m/s
C. 该质点振动周期为8s
D. 再过0.04s,x=4m处的质点在平衡位置且向上运动
【答案】B
【解析】
【分析】
本题考查波的图像与振动图像的区别与联系、波的形成与传播、波长、频率、波速之间的关系应用等。
根据t=0时刻x=6m处质点的振动方向得到波的传播方向,由左图得到波长,右图得到周期,根据v=λT?求解波速;关键明确波形平移方向与质点振动方向的关系,能够结合公式v=λT求解波速。
【解答】
A.t=0时刻x=6m处质点的振动方向是向上,由波形平移法知,波沿x轴负方向传播,故A错误;
BC.由左图得到波长为λ=8m,右图得到周期为T=0.08s,故波速v=λT=100m/s,故B正确,C错误;
D.再过0.04s,波向x负向传播的距离为:Δx=vΔt=100×0.04m=4m,即再过0.04s,平衡位置在x=8m处的质点的振动形式传播到x=4m处,故再过0.04s,x=4m处的质点在正向最大位移处,将要向下运动,故D错误。
故选B。
一列简谐横波在某一时刻的波形图如图中实线所示,经0.2?s后,其波形如图中虚线所示。则该简谐波的波速不可能是(? ? )
center0A. 2.1?m/s B. 3.9?m/s C. 7.2?m/s D. 14.1?m/s
【答案】C
【解析】
【分析】
本题是波动图象中典型的问题,要根据波的周期性和双向性研究时间与周期的关系,熟练运用波形平移法研究。由图可知波的波长,而由两列波的波形图可得两波形相距的时间与周期的关系,则可得出波速的表达式。
【解答】
由图可知,波的波长为0.24m,如果波向右传播,0.2=(n+34)T,得到波速v=λT=(1.2n+0.90)m/s,(n=0,1,2,3...),当n=1时,v=2.1m/s,当n=11时,v=14.1m/s;
如果波向左传播,0.2=(n+14)T,得到波速v=λT=(1.2n+0.3)m/s,(n=0,1,2,3...)当n=3时,v=3.9m/s,故ABD正确,C错误。
故选C。
二、多选题
一列简谐横波沿x轴传播,t=0和t=0.20s时的波形分别如图中实线和虚线所示。已知t=0.20s时,x=2cm位置的质点处于平衡位置,该波的周期T>0.30s。下列说法正确的是(????)
center0A. 该波的周期T=1.6s
B. 该波沿x轴正方向传播,波速为0.7m/s
C. x=0位置的质点在t=0.4s时处于平衡位置
D. x=16cm位置的质点在t=0.12s时处于波谷
【答案】AC
【解析】解:AB.若波向负方向传播,则传播时间和周期的关系为t=0.2s=18T+nT,
所以周期为T=1.68n+1(n=0、1、2…)
因为T>0.30s,所以n=0,周期T=1.6s,传播速度为v=λT=161.6cm/s=0.1m/s,
若波向正方向传播,则传播时间t=78T+nT,
故周期为T=1.68n+7(n=0、1、2…),
由于不论n取什么,都不能满足周期T>0.30s,所以波向左传播,周期为1.6s,故A正确,B错误;
C.由图象可知,x=0位置的质点在t=0时处于波峰位置,因为t=0.4s=14T,所以x=0的质点振动到平衡位置,故C正确;
D.因为t=0.12s介于0-14T之间,故x=16cm位置的质点在波谷到平衡位置之间,故D错误;
故选:AC。
(1)根据图象特征找到传播世间与周期的关系,再根据周期条件找到周期的值;
(2)根据v=λT求解波速;
(3)根据选项所给时间结合初始的振动方向判断质点在t=0.4s和0.12s时的位置;
知道波的多解性,会根据图形找到时间和周期的关系,会根据图象找到有用的信息;
如图所示,一列简谐横波沿x轴正方向传播,在t1=0时刻波传播到x=2?m处的质点C,此时x=0.5?m处的质点A在负方向最大位移处,在t2=0.3?s时刻质点A处于平衡位置且向下振动,则下列判断正确的是
center0A. 该简谐横波的波速可能等于5 m/s
B. 质点C开始振动时的运动方向沿y轴负方向
C. 在t1~t2时间内,x=1 m处的质点B通过的路程可能大于6.0 cm
D. 在t2时刻,位于x=3 m处的质点D处于负方向最大位移处
【答案】AC
【解析】
【分析】
根据A的振动情况确定周期,根据波动图象得出波长,根据v=λT求解波速;根据波的传播方向判断质点的振动方向;根据质点在一个周期内振动的通过的路程为4A求解路程;根据波的传播判断质点D的位置。
本题关键是根据质点A的振动情况得出周期的通式,注意波传播的周期性导致的多解问题。
【解答】
A.t2=0.3s时质点A处于平衡位置且向下振动,则n+34T=0.3s? ( n=0,1,2,3?),T=1.24n+3s? ( n=0,1,2,3?),由图可知,λ=2m,所以v=λT=54n+33m/s? ( n=0,1,2,3?),n=0时,v=5m/s,故A正确;
B.波沿x轴正方向传播,C点开始振动方向为y轴正方向,故B错误;
C.T=1.24n+3s? ( n=0,1,2,3?),若n=0,即周期T=0.4s,则在t1~t2时间内,x=1m处的质点B从平衡位置开始振动34个周期,通过的路程为s=34×4A=6.0cm,若n?1则在t1~t2时间内,x=1m处的质点B从平衡位置开始振动n+34个周期,通过的路程为s=n+34×4A=2.0×4n+3cm>6.0cm,故C正确;
D.经过0.3s时该波沿正方向传播了x=vt=4n+32m,所以位于x=3m处的质点D处于正方向最大位移处,故D错误。
???????故选AC。
如图,a、b、c、d是均匀媒质x轴上的四个质点,相邻两点的间距依次为4?m、8?m和16?m。一列简谐横波以4?m/s的波速沿x轴正向传播,在t=?10?s时刻到达质点c处,质点c由平衡位置开始垂直x轴向上运动,t=?13?s时c第一次到达最低点。则
A. 在t=?7s时刻质点a垂直x轴向上运动
B. 在t=?9s时刻质点b恰好到达最高点
C. 在t=?15s时刻a、d之间有两个波谷
D. 在15?s?【答案】ABC
【解析】
【分析】
由题“在t=0时刻到达质点a处,质点a由平衡位置开始竖直向下运动,t=13s时a第一次到达最高点”可确定出该波的周期.根据a与d间的距离,由t=xv求出波从a传到d的时间.根据时间t=10s与周期的关系,分析质点c的状态.
本题关键要抓住波在同一介质中是匀速传播的,由t=xv可求出波传播的时间.要抓住各个质点的起振方向都与波源的起振方向相同,通过分析波的形成过程进行分析.
【解答】
A.设该波的周期为T,由题可得,34T=3s,得T=4s.波从a传到c的时间为t=xv=4+84s=3s,则在t=7s时刻质点a开始起振,A正确;
B. 波从b传到c的时间为t=xv=84s=2s?,b点8s时起振,t?=?9s时刻质点b恰好到达最高点,B正确;
C.该波的波长:λ=vT=4×4=16m,而ad之间的距离:x'=4m+8m+16m=28m=84λ,此时a振动了两个周期,处于平衡位置向上振动,故可根据波形图推断D处于波峰,在t?=?15s时刻a、d之间有两个波谷,C正确;
D.波从c传到d的时间为t=xv=164s=4s,故d在14s时开始起振,在15?s时处于波峰,开始向下振动,D错误;?
故选:ABC.
三、计算题
一列简谐横波图象如下图所示,t1时刻的波形如图中实线所示,t2时刻的波形如图中虚线所示,已知Δt=t2-t1=0.5s,问:
(1)这列波的可能波速的表达式?
(2)若波向左传播,且3T<Δt<4T,波速多大?
(3)若波速ν=68m/s,则波向哪个方向传播?
【答案】解:(1)若波向右传播,根据波形的周期性,v=xt=(8n+2)0.5m/s=16n+4m/s(n=0,1,2,?)?①
同理可得,若波向左传播,v=16n+12m/s(n=0,1,2,?)?②
(2)若波向左传播,且3T<△t<4T,则由v=16n+12m/s
得:v=16×3+12m/s=60m/s
(3)假设波向右传播,将v=68m/s
代入?①得,68=16n+4,n=4,假设成立,故波向右传播
答:(1)这列波的可能波速的表达式为:v=16n+4m/s或v=16n+12m/s(n=0,1,2,?);
(2)若波向左传播,且3T<△t<4T,波速60m/s;
(3)若波速v=68m/s,则波向右传播
【解析】略
如图是某横波的波形图,实线表示某时刻的波形,虚线表示0.2s后的波形图.
(1)若波向左传播,则它传播的可能距离是多少?
(2)若波向右传播,则它的最大周期是多少?
(3)若波速为35m/s,则波的传播方向如何?
【答案】解:(1)若向左传播,Δt时间内波传播的距离为Δx=(n+34)λ? (n=0,1,2…)
其中λ=4m
得到x=(4n+3)m,(n=0,1,2…),
可能距离为3m、7m、11m…
(2)当波向右传播时,和周期T的关系为
1,2…)
所以T=0.84n+1s(n=0,1,2…)
当n=0时,T有最大值Tmax=0.80+1s=0.8s
(3)波在内传播的距离为
结合图形可判断出波是向左传播的。
【解析】(1)波形的平移法可知,波向左传播的最小距离等于34波长,由波的周期性,写出波传播的可能距离;
(2)当波向右传播时,写出和周期T的关系,得到周期的通式,求解最大周期;
(3)由△x=vt求出波传播的距离,由波形的平移法确定波的传播方向。
本题知道两个时刻的波形,要根据波的周期性和双向性进行研究,往往会得到波传播距离和周期的通项,再得到特殊值。
一列简谐横波在t=13s的波形图如图(a)所示,P、Q是介质中的两个质点,图(b)是质点Q的振动图象。求:
(i)波速及波的传播方向;
(ii)质点Q的平衡位置的x坐标。
【答案】解:(i)由图(a)可以看出,该波的波长为λ=36cm,
由图(b)可以看出周期T=2s,
故波速为v=λT=18cm/s,
由(b)可知,当t=13s时,Q向上振动,结合图(a)可知,该波沿x轴负方向传播;
(ii)设质点P、Q的平衡位置的x轴坐标分别为xP、xQ,由图(a)可知,x=0处y=-A2=Asin(-30°)
因此xP=30°360?λ=3cm
由图(b)可知,在t=0时Q点处于平衡位置,经过△t=13s,其振动状态向x轴负方向传播到P点处,
所以xQ-xP=v△t=6cm,
解得质点Q的平衡位置的x坐标为xQ=9cm。
【解析】(i)由图(a)得到波长,由图(b)得到周期,根据v=λT计算波速,根据振动情况确定传播方向;
(ii)首先确定P点平衡位置横坐标,再根据向x轴负方向传播到P点处经过的时间,由此求出质点Q的平衡位置的x坐标。
本题主要是考查了波的图象;解答本题关键是要掌握振动的一般方程y=Asinωt,知道方程中各字母表示的物理意义,能够根据图象直接读出振幅、波长和各个位置处的质点振动方向,知道波速、波长和频率之间的关系。
如图所示,图甲是一列简谐横波在t=0时刻的波形图,P点是此时处在平衡位置的一个质点.图乙是质点P的振动图象.
(1)判断这列波的传播方向;
(2)经过时间t1=6s,质点P通过的路程s;
(3)经过t2=30s,波向前传播的距离x.
【答案】解:(1)由图乙知,t=0时刻质点P正向上振动,所以根据波形平移法知,该波沿x轴正方向传播;
(2)从图乙可知振动周期为T=4s,一个周期内质点通过的路程为4A,则经过时间t1=6s=1.5T,质点P通过的路程为:s=1.5×4A=6×2cm=12cm;
(3)波速为:v=λT=84m/s=2m/s。
经过t2=30s,波向前传播的距离x=vt2=2×30m=40m。
答:(1)这列波的传播方向沿x轴正方向;
(2)经过时间t1=6s,质点P通过的路程s是12cm;
(3)经过t2=30s,波向前传播的距离x是60m。
【解析】本题的关键要把握振动图象和波动图象的内在联系.要注意两种图象判断质点振动方向方法的区别,波动图象常用波形平移法判断质点的振动方向.而振动图象常用斜率分析质点的振动方向。
(1)根据振动图象判断出t=0时刻P点的振动方向,再判断波的传播方向;
(2)图乙读出周期,由周期与时间的关系,结合题意,即可求解P点通过的路程;
(3)由公式v=λT求出波速,由x=vt求解波传播的距离。
四、综合题
(1)一简谐机械横波沿x轴负方向传播,已知波的波长为8?m,周期为2?s,t=1?s时刻波形如图甲所示,a、b、d是波上的三个质点。图乙是波上某一点的振动图像。则下列说法正确的是(????)(填正确答案标号。)
A.图乙可以表示d质点的振动
B.图乙可以表示b质点的振动
C.a、b两质点在t=1.5?s时速度大小相同
D.该波传播速度为v=4?m/s
E.t=0时b质点速度沿y轴正方向
(2)如图中实线是一列简谐横波在t1=0时刻的波形,虚线是这列波在t2=0.5?s时刻的波形。
(1)写出这列波的波速表达式;
(2)若波速大小为74?m/s,波速方向如何?
【答案】(1)?ADE;
(2)解:(1)由题图图像可知λ=8?m?
当波向右传播时,波传播距离为
s=nλ+38λ=(8n+3)m(n=0,1,2…)
波速为v=sΔt=8n+30.5?m/s=(16n+6)?m/s(n=0,1,2…)。?
当波向左传播时,波传播距离为
s=nλ+58λ=(8n+5)?m(n=0,1,2…)?
波速为v=sΔt=8n+50.5?m/s=(16n+10)m/s(n=0,1,2…)。?
(2)若波速大小为74?m/s,在Δt=t2-t1时间内波传播的距离为s=v·Δt=74×0.5?m=37?m。?
因为37?m=4λ+58λ,所以波向左传播。?
【解析】
(1)
【分析】
本题既要能理解振动图象和波动图象各自的物理意义,又要抓住它们之间内在联系,能熟练根据波的传播方向判断出质点的速度方向。
质点的速度和加速度可根据质点的位置进行判断。在平衡位置时,速度最大,加速度最小;在最大位移处,速度为零,加速度最大。根据图乙中t=0时刻质点的位置和振动方向,在图甲上找出对应的质点;再根据波长、周期和频率的关系即可确定传播速度,根据带动法确定各质点的振动方向。
【解答】
AB.由图乙知,t=1s时刻质点经过平衡位置向上运动,图甲是t=1s时刻的波形,此时a位于波峰,位移最大,与图乙中t=1s时刻质点的状态不符,而质点b在t=1s时刻经过平衡位置向下运动,与图乙中t=1时刻质点的状态不符,而质点d在t=1s时刻经过平衡位置向上运动,所以图乙不能表示质点b的振动,可以表示质点d的振动,故 A正确, B错误。
C.ab两质点相差四分之一个周期,t=1.5s,则△t=0.5s=0.25T时,质点a位于平衡位置,质点b处于波谷,速度大小不可能相等,故 C错误。
D.波的波长为8m,周期为2s,故传播速度v=λT=82m/s=4m/s,故D正确;
E.根据平移法可知,t=0时b点速度沿y轴正方向,故 E正确。
故选ADE。
(2)
本题考查了波传播的多解性,分情况讨论。
(1)波传播存在两种可能,向左或向右传播,根据题干信息,?利用波速公式求解。
(2)由s=vt求出波传播的距离,分析与波长的关系,确定波传播的方向。
(1)图(a)为一列简谐横波在t=2s时的波形图,图(b)为介质中平衡位置在x=2.5m处的质点的振动图象,P是平衡位置为x=1m的质点,下列说法正确的是_________.
A.波速为0.5m/s
B.波的传播方向向左
C.0~1.5s,P运动的路程为6cm
D.3s~5s,P振动方向发生变化
E.t=9s时,P的加速度恰好为零
(2)如图所示,直角玻璃三棱镜置于空气中,已知∠A=60°,∠C=90°,一束极细的光于AC的中点D垂直AC面入射,棱镜的折射率为n=2。
①求此玻璃对空气的临界角;
②光从棱镜第一次射入空气时的折射角。
【答案】(1)ADE;
(2)解:①设玻璃对空气的临界角为C,则sinC=1n=12???
所以
②如图所示因为i1=60°>C,所以光线在AB面上将发生全反射
由几何知识得?i2=i1-30°=30°得r=45°
【解析】
(1)【分析】
先根据质点的振动图象,判断波的传播方向,再根据波长和周期求波速;据波形成的条件和特点分析各质点的振动情况。
本题考查了横波的图像,波长、频率和波速的关系;熟练利用波形平移法判断质点的振动方向与传播方向、利用周期表示时间,求质点的路程、注意时间和空间周期性的对应。
【解答】
A.由图(a)可知该简谐横波波长为2m,由图(b)知周期为4s,则波速为v=λT=0.5m/s,故A正确;
B.根据图(b)的振动图象可知,在x=2.5m处的质点在t=2s时振动方向向下,由同侧法可知该波向右传播,故B错误;
C.由波的平移法可知,0时刻P质点位移波谷,从此位置开始经过1.5s即八分之三周期,则P运动的路程大于6cm,故C错误;
D.t=2s时P质点位于波峰,经过四分之一周期即1s后,P质点向下运动到平衡位置,再经过1s,P质点向下运动位于波谷,接着反向向上振动,故D正确;
E.从图(a)所示再经过9s,即经过214T,质点P恰好经过平衡位置,则此时的加速度为0,故E正确。
故选ADE。
(2)本题考查了光的折射和光的全反射,光学问题分析计算的关键是正确的画出光路图。
①根据临界角公式计算玻璃对空气的临界角;
②根据光路图结合临界角分析光从哪个面第一次射入空气,根据几何关系结合折射定律计算折射角。
(1)如图为一列传播速率v=8m/s的简谐横波在t=0时刻的波形图,P是平衡位置为x1=3.5m处的质点,Q是平衡位置为x2=26m处的质点,此时质点P正做减速运动,则(????)
A. 该波沿x轴负方向传播
B.t=2.5s时,Q质点开始振动
C.Q质点的起振方向沿y轴正向
D.t=2.7s时质点Q向y轴正方向加速运动
E.?1s内质点P通过的路程为40 cm
(2)如图所示,小玻璃球的半径为R,折射率n=3,今有一束细光束从与直径相距d=32R的点,沿直径方向照在小玻璃球上,入射光线可经过折射、反射、折射,再射出后恰能平行于原射入方向返回。已知光在真空中的传播速度为c,求该细光束在玻璃球中的传播时间。
center0
【答案】(1)BCE
(2)解:画出光路图如图,设入射点C对应的入射角为θ1,折射角为θ2,
由几何关系可得sinθ1=dR=32,所以θ1=60?
由折射定律sinθ1sinθ2=n得:θ2=30?
所以BC长l=2Rcosθ2=3R??
由对称性可知总路程为x=2l=4Rcosθ2=23R??
设玻璃球中的光速为v,由n=cv得v=c3????
所以传播时间t=xv=6Rc??
【解析】
(1)【分析】
由题图可读出振幅A,波长,由?T=λv可得周期,由质点P正做减速运动,据质点振动方向和波的传播方向的关系可知该波的传播方向,分析周期与t=2.5s的关系,判断t=2.7s时质点Q的振动方向,1s内质点P通过的路程为振幅的8倍。
【解答】
A.由质点P正做减速运动可知t=0时刻P向下运动,据质点振动方向和波的传播方向的关系可知该波沿x轴正方向传播,A错误。
BD.经过2.5s时间,Q点开始振动,?T4<0.2sC.波源的起振方向与x=6m的质点t=0时刻的振动方向相同,简谐波沿x轴正方向传播,可知x=6m的质点在t=0时刻的振动方向向上,则波源的起振方向向上,进而可知Q质点的起振方向沿y轴正方向,故C正确;
E.由题图可读出振幅A=5cm,波长λ=4m,由?T=λv可得周期为0.5s,1s内,即两个周期内,质点P通过的路程为振幅的8倍,即40cm,E正确。
故选BCE。
(2)画出光路图,由几何知识和折射定律求出光线在玻璃中的传播距离,由t=xv
进而可求出时间。本题考查了折射定律的应用,正确作出光路图,灵活运用几何知识求解是关键。
(1)一列简谐横波在同种均匀介质中传播,某时刻波形如图甲所示。由该时刻开始计时,质点L的振动情况如图乙所示。下列说法正确的是(????)
A.该横波沿x轴正方向传播
B.质点N该时刻向y轴正方向运动
C.质点L经半个周期将沿x轴正方向移动
D.该时刻质点K与M的速度、加速度大小都相同
E.从该时刻起,质点O与质点N的振动情况始终相同
(2)如图所示,圆心为O、半径为R的半圆形玻璃砖置于水平面上,当入射角为θ时,光线从玻璃砖P点射入后,直接从圆形表面顶端B点射出,已知OP=2R2,sinθ=63,真空中的光速为c.求:
Ⅰ.玻璃砖的折射率n;
Ⅱ.当光线垂直OP边从P点入射时,光在玻璃中传播所用的时间t。
【答案】(1)ADE;
(2)解:Ⅰ.作出两种情况下的光路图,如图所示
由于sin∠OBP=2R2(2R2)2+R2
在B处射出,故∠OBP=∠BPA
n=sinθsin∠BPA
联立可得n=2
Ⅱ.光在玻璃中的传播速度v
v=cn
当光线垂直OP边从P点入射时:
sin∠OAP=22RR=22????sinC=1n=22
所以∠OAP=C=45°,光线在玻璃中发生全反射,从与P点对称的Q点射出,
t=4?OPv
解得t=4Rc
【解析】
(1)
【分析】
本题要掌握用微平移法判断质点的振动方向和波的传播方向,知道质点不会随波迁移,理解波动图象与振动图象的区别,注意速度与加速度是矢量,是否相同还要考虑其方向。
根据质点L的振动图象,从而判定波的传播方向,再依据波的微平移法,则可确定质点N点的振动方向,波在传播过程中,质点不随波迁移;最后结合速度与加速度是矢量,是否相等要从大小与方向两角度考虑。
【解答】
A.由图乙可知,质点L在该时刻,向y轴正方向振动,依据微平移法,可知,该横波沿x轴正方向传播,故A正确;
B.由上分析,结合微平移法,可知,质点N该时刻向y轴负方向运动,故B错误;
C.依据机械波在传播过程中质点并不随波一起迁移,因此质点L经半个周期不会沿x轴正方向移动到N点,故C错误;
D.因K、M之间间隔半个波长,K、M的步调始终相反,因此该时刻质点K与M的速度、加速度大小都相同,但它们的方向不同,故D正确;
E.由图知质点O与质点N间隔一个波长,所以质点O与质点N的振动情况始终相同,故E正确。
故选ADE。
(2)
本题主要是考查了光的折射和光的全发射;解答此类题目的关键是弄清楚光的传播情况,画出光路图,根据图中的几何关系,根据光的折射定律、全反射的条件求解。
一、单选题
一列简谐横波在某一时刻的波形图如图中实线所示,经0.2?s后,其波形如图中虚线所示。则该简谐波的波速不可能是(?)
A. 2.1?m/s B. 3.9?m/s C. 7.2?m/s D. 14.1?m/s
一列简谐横波沿x轴传播,图甲是t=1.0s时的波形图,图乙是x=3.0m处质点的振动图像,a、b质点在x轴上平衡位置分别为xa=0.5m、xb=2.5m,下列说法正确的是
A. 波沿x轴正方向传播
B. 波的传播速度为0.5?m/s
C. t=1.5?s时,a、b两点的速度和加速度均等大反向
D. 从t=1.0?s到t=1.5?s质点a的路程为10?cm
如图所示分别为一列横波在某一时刻的图像和在x=6m处的质点从该时刻开始计时的振动图像,则这列波(????)
A. 沿x轴的正方向传播
B. 波速为100m/s
C. 该质点振动周期为8s
D. 再过0.04s,x=4m处的质点在平衡位置且向上运动
一列简谐横波在某一时刻的波形图如图中实线所示,经0.2?s后,其波形如图中虚线所示。则该简谐波的波速不可能是(? ? )
A. 2.1?m/s B. 3.9?m/s C. 7.2?m/s D. 14.1?m/s
二、多选题
一列简谐横波沿x轴传播,t=0和t=0.20s时的波形分别如图中实线和虚线所示。已知t=0.20s时,x=2cm位置的质点处于平衡位置,该波的周期T>0.30s。下列说法正确的是(????)
A. 该波的周期T=1.6s
B. 该波沿x轴正方向传播,波速为0.7m/s
C. x=0位置的质点在t=0.4s时处于平衡位置
D. x=16cm位置的质点在t=0.12s时处于波谷
如图所示,一列简谐横波沿x轴正方向传播,在t1=0时刻波传播到x=2?m处的质点C,此时x=0.5?m处的质点A在负方向最大位移处,在t2=0.3?s时刻质点A处于平衡位置且向下振动,则下列判断正确的是
A. 该简谐横波的波速可能等于5 m/s
B. 质点C开始振动时的运动方向沿y轴负方向
C. 在t1~t2时间内,x=1 m处的质点B通过的路程可能大于6.0 cm
D. 在t2时刻,位于x=3 m处的质点D处于负方向最大位移处
如图,a、b、c、d是均匀媒质x轴上的四个质点,相邻两点的间距依次为4?m、8?m和16?m。一列简谐横波以4?m/s的波速沿x轴正向传播,在t=?10?s时刻到达质点c处,质点c由平衡位置开始垂直x轴向上运动,t=?13?s时c第一次到达最低点。则
A. 在t=?7s时刻质点a垂直x轴向上运动
B. 在t=?9s时刻质点b恰好到达最高点
C. 在t=?15s时刻a、d之间有两个波谷
D. 在15?s?
一列简谐横波图象如下图所示,t1时刻的波形如图中实线所示,t2时刻的波形如图中虚线所示,已知Δt=t2-t1=0.5s,问:
(1)这列波的可能波速的表达式?
(2)若波向左传播,且3T<Δt<4T,波速多大?
(3)若波速ν=68m/s,则波向哪个方向传播?
如图是某横波的波形图,实线表示某时刻的波形,虚线表示0.2s后的波形图.
(1)若波向左传播,则它传播的可能距离是多少?
(2)若波向右传播,则它的最大周期是多少?
(3)若波速为35m/s,则波的传播方向如何?
一列简谐横波在t=13s的波形图如图(a)所示,P、Q是介质中的两个质点,图(b)是质点Q的振动图象。求:
(i)波速及波的传播方向;
(ii)质点Q的平衡位置的x坐标。
如图所示,图甲是一列简谐横波在t=0时刻的波形图,P点是此时处在平衡位置的一个质点.图乙是质点P的振动图象.
(1)判断这列波的传播方向;
(2)经过时间t1=6s,质点P通过的路程s;
(3)经过t2=30s,波向前传播的距离x.
四、综合题
(1)一简谐机械横波沿x轴负方向传播,已知波的波长为8?m,周期为2?s,t=1?s时刻波形如图甲所示,a、b、d是波上的三个质点。图乙是波上某一点的振动图像。则下列说法正确的是(????)(填正确答案标号。)
A.图乙可以表示d质点的振动
B.图乙可以表示b质点的振动
C.a、b两质点在t=1.5?s时速度大小相同
D.该波传播速度为v=4?m/s
E.t=0时b质点速度沿y轴正方向
(2)如图中实线是一列简谐横波在t1=0时刻的波形,虚线是这列波在t2=0.5?s时刻的波形。
(1)写出这列波的波速表达式;
(2)若波速大小为74?m/s,波速方向如何?
(1)图(a)为一列简谐横波在t=2s时的波形图,图(b)为介质中平衡位置在x=2.5m处的质点的振动图象,P是平衡位置为x=1m的质点,下列说法正确的是_________.
A.波速为0.5m/s
B.波的传播方向向左
C.0~1.5s,P运动的路程为6cm
D.3s~5s,P振动方向发生变化
E.t=9s时,P的加速度恰好为零
(2)如图所示,直角玻璃三棱镜置于空气中,已知∠A=60°,∠C=90°,一束极细的光于AC的中点D垂直AC面入射,棱镜的折射率为n=2。
①求此玻璃对空气的临界角;
②光从棱镜第一次射入空气时的折射角。
(1)如图为一列传播速率v=8m/s的简谐横波在t=0时刻的波形图,P是平衡位置为x1=3.5m处的质点,Q是平衡位置为x2=26m处的质点,此时质点P正做减速运动,则(????)
A. 该波沿x轴负方向传播
B.t=2.5s时,Q质点开始振动
C.Q质点的起振方向沿y轴正向
D.t=2.7s时质点Q向y轴正方向加速运动
E.?1s内质点P通过的路程为40 cm
(2)如图所示,小玻璃球的半径为R,折射率n=3,今有一束细光束从与直径相距d=32R的点,沿直径方向照在小玻璃球上,入射光线可经过折射、反射、折射,再射出后恰能平行于原射入方向返回。已知光在真空中的传播速度为c,求该细光束在玻璃球中的传播时间。
而可求出时间。本题考查了折射定律的应用,正确作出光路图,灵活运用几何知识求解是关键。
(1)一列简谐横波在同种均匀介质中传播,某时刻波形如图甲所示。由该时刻开始计时,质点L的振动情况如图乙所示。下列说法正确的是(????)
A.该横波沿x轴正方向传播
B.质点N该时刻向y轴正方向运动
C.质点L经半个周期将沿x轴正方向移动
D.该时刻质点K与M的速度、加速度大小都相同
E.从该时刻起,质点O与质点N的振动情况始终相同
(2)如图所示,圆心为O、半径为R的半圆形玻璃砖置于水平面上,当入射角为θ时,光线从玻璃砖P点射入后,直接从圆形表面顶端B点射出,已知OP=2R2,sinθ=63,真空中的光速为c.求:
Ⅰ.玻璃砖的折射率n;
Ⅱ.当光线垂直OP边从P点入射时,光在玻璃中传播所用的时间t。
3.2播的描述
一、单选题
一列简谐横波在某一时刻的波形图如图中实线所示,经0.2?s后,其波形如图中虚线所示。则该简谐波的波速不可能是(?)
center0A. 2.1?m/s B. 3.9?m/s C. 7.2?m/s D. 14.1?m/s
【答案】C
【解析】
【分析】
本题是波动图象中典型的问题,要根据波的周期性和双向性研究时间与周期的关系,熟练运用波形平移法研究。由图可知波的波长,而由两列波的波形图可得两波形相距的时间与周期的关系,则可得出波速的表达式。
【解答】
由图可知,波的波长为0.24m,如果波向右传播,0.2=(n+34)T,得到波速v=λT=(1.2n+0.90)m/s,(n=0,1,2,3...),当n=1时,v=2.1m/s,当n=11时,v=14.1m/s;
如果波向左传播,0.2=(n+14)T,得到波速v=λT=(1.2n+0.3)m/s,(n=0,1,2,3...)当n=3时,v=3.9m/s,故ABD正确,C错误。
故选C。
一列简谐横波沿x轴传播,图甲是t=1.0s时的波形图,图乙是x=3.0m处质点的振动图像,a、b质点在x轴上平衡位置分别为xa=0.5m、xb=2.5m,下列说法正确的是
center0A. 波沿x轴正方向传播
B. 波的传播速度为0.5?m/s
C. t=1.5?s时,a、b两点的速度和加速度均等大反向
D. 从t=1.0?s到t=1.5?s质点a的路程为10?cm
【答案】C
【解析】
【分析】
本题考查波的图像和振动图像,关键是能够从图像中分析出波的传播信息和质点的振动信息,基础题。
根据图像结合“上坡下,下坡上”的规律分析波的传播方向;根据波长、波速和周期关系计算波速;根据平移法分析a、b质点振动情况及路程。
【解答】,
A.t=1s时,x=3.0m处质点向y轴正方向振动,根据“上坡下,下坡上”可知波沿x轴负方向传播,故A错误;
B.根据图像可知该波波长λ=4m,周期T=2s,故波的传播速度为v=λT=2m/s,故B错误;
C.根据波的平移,可知t=1.5s时,a质点在y=-52cm位置向y轴负方向振动,b质点在y=52cm位置向y轴正方向振动,故a、b两点的速度和加速度均等大反向,故C正确;
D.从t=1.0s到t=1.5s质点a的路程为102cm,故D错误。
故选C。
如图所示分别为一列横波在某一时刻的图像和在x=6m处的质点从该时刻开始计时的振动图像,则这列波(????)
center0A. 沿x轴的正方向传播
B. 波速为100m/s
C. 该质点振动周期为8s
D. 再过0.04s,x=4m处的质点在平衡位置且向上运动
【答案】B
【解析】
【分析】
本题考查波的图像与振动图像的区别与联系、波的形成与传播、波长、频率、波速之间的关系应用等。
根据t=0时刻x=6m处质点的振动方向得到波的传播方向,由左图得到波长,右图得到周期,根据v=λT?求解波速;关键明确波形平移方向与质点振动方向的关系,能够结合公式v=λT求解波速。
【解答】
A.t=0时刻x=6m处质点的振动方向是向上,由波形平移法知,波沿x轴负方向传播,故A错误;
BC.由左图得到波长为λ=8m,右图得到周期为T=0.08s,故波速v=λT=100m/s,故B正确,C错误;
D.再过0.04s,波向x负向传播的距离为:Δx=vΔt=100×0.04m=4m,即再过0.04s,平衡位置在x=8m处的质点的振动形式传播到x=4m处,故再过0.04s,x=4m处的质点在正向最大位移处,将要向下运动,故D错误。
故选B。
一列简谐横波在某一时刻的波形图如图中实线所示,经0.2?s后,其波形如图中虚线所示。则该简谐波的波速不可能是(? ? )
center0A. 2.1?m/s B. 3.9?m/s C. 7.2?m/s D. 14.1?m/s
【答案】C
【解析】
【分析】
本题是波动图象中典型的问题,要根据波的周期性和双向性研究时间与周期的关系,熟练运用波形平移法研究。由图可知波的波长,而由两列波的波形图可得两波形相距的时间与周期的关系,则可得出波速的表达式。
【解答】
由图可知,波的波长为0.24m,如果波向右传播,0.2=(n+34)T,得到波速v=λT=(1.2n+0.90)m/s,(n=0,1,2,3...),当n=1时,v=2.1m/s,当n=11时,v=14.1m/s;
如果波向左传播,0.2=(n+14)T,得到波速v=λT=(1.2n+0.3)m/s,(n=0,1,2,3...)当n=3时,v=3.9m/s,故ABD正确,C错误。
故选C。
二、多选题
一列简谐横波沿x轴传播,t=0和t=0.20s时的波形分别如图中实线和虚线所示。已知t=0.20s时,x=2cm位置的质点处于平衡位置,该波的周期T>0.30s。下列说法正确的是(????)
center0A. 该波的周期T=1.6s
B. 该波沿x轴正方向传播,波速为0.7m/s
C. x=0位置的质点在t=0.4s时处于平衡位置
D. x=16cm位置的质点在t=0.12s时处于波谷
【答案】AC
【解析】解:AB.若波向负方向传播,则传播时间和周期的关系为t=0.2s=18T+nT,
所以周期为T=1.68n+1(n=0、1、2…)
因为T>0.30s,所以n=0,周期T=1.6s,传播速度为v=λT=161.6cm/s=0.1m/s,
若波向正方向传播,则传播时间t=78T+nT,
故周期为T=1.68n+7(n=0、1、2…),
由于不论n取什么,都不能满足周期T>0.30s,所以波向左传播,周期为1.6s,故A正确,B错误;
C.由图象可知,x=0位置的质点在t=0时处于波峰位置,因为t=0.4s=14T,所以x=0的质点振动到平衡位置,故C正确;
D.因为t=0.12s介于0-14T之间,故x=16cm位置的质点在波谷到平衡位置之间,故D错误;
故选:AC。
(1)根据图象特征找到传播世间与周期的关系,再根据周期条件找到周期的值;
(2)根据v=λT求解波速;
(3)根据选项所给时间结合初始的振动方向判断质点在t=0.4s和0.12s时的位置;
知道波的多解性,会根据图形找到时间和周期的关系,会根据图象找到有用的信息;
如图所示,一列简谐横波沿x轴正方向传播,在t1=0时刻波传播到x=2?m处的质点C,此时x=0.5?m处的质点A在负方向最大位移处,在t2=0.3?s时刻质点A处于平衡位置且向下振动,则下列判断正确的是
center0A. 该简谐横波的波速可能等于5 m/s
B. 质点C开始振动时的运动方向沿y轴负方向
C. 在t1~t2时间内,x=1 m处的质点B通过的路程可能大于6.0 cm
D. 在t2时刻,位于x=3 m处的质点D处于负方向最大位移处
【答案】AC
【解析】
【分析】
根据A的振动情况确定周期,根据波动图象得出波长,根据v=λT求解波速;根据波的传播方向判断质点的振动方向;根据质点在一个周期内振动的通过的路程为4A求解路程;根据波的传播判断质点D的位置。
本题关键是根据质点A的振动情况得出周期的通式,注意波传播的周期性导致的多解问题。
【解答】
A.t2=0.3s时质点A处于平衡位置且向下振动,则n+34T=0.3s? ( n=0,1,2,3?),T=1.24n+3s? ( n=0,1,2,3?),由图可知,λ=2m,所以v=λT=54n+33m/s? ( n=0,1,2,3?),n=0时,v=5m/s,故A正确;
B.波沿x轴正方向传播,C点开始振动方向为y轴正方向,故B错误;
C.T=1.24n+3s? ( n=0,1,2,3?),若n=0,即周期T=0.4s,则在t1~t2时间内,x=1m处的质点B从平衡位置开始振动34个周期,通过的路程为s=34×4A=6.0cm,若n?1则在t1~t2时间内,x=1m处的质点B从平衡位置开始振动n+34个周期,通过的路程为s=n+34×4A=2.0×4n+3cm>6.0cm,故C正确;
D.经过0.3s时该波沿正方向传播了x=vt=4n+32m,所以位于x=3m处的质点D处于正方向最大位移处,故D错误。
???????故选AC。
如图,a、b、c、d是均匀媒质x轴上的四个质点,相邻两点的间距依次为4?m、8?m和16?m。一列简谐横波以4?m/s的波速沿x轴正向传播,在t=?10?s时刻到达质点c处,质点c由平衡位置开始垂直x轴向上运动,t=?13?s时c第一次到达最低点。则
A. 在t=?7s时刻质点a垂直x轴向上运动
B. 在t=?9s时刻质点b恰好到达最高点
C. 在t=?15s时刻a、d之间有两个波谷
D. 在15?s?
【解析】
【分析】
由题“在t=0时刻到达质点a处,质点a由平衡位置开始竖直向下运动,t=13s时a第一次到达最高点”可确定出该波的周期.根据a与d间的距离,由t=xv求出波从a传到d的时间.根据时间t=10s与周期的关系,分析质点c的状态.
本题关键要抓住波在同一介质中是匀速传播的,由t=xv可求出波传播的时间.要抓住各个质点的起振方向都与波源的起振方向相同,通过分析波的形成过程进行分析.
【解答】
A.设该波的周期为T,由题可得,34T=3s,得T=4s.波从a传到c的时间为t=xv=4+84s=3s,则在t=7s时刻质点a开始起振,A正确;
B. 波从b传到c的时间为t=xv=84s=2s?,b点8s时起振,t?=?9s时刻质点b恰好到达最高点,B正确;
C.该波的波长:λ=vT=4×4=16m,而ad之间的距离:x'=4m+8m+16m=28m=84λ,此时a振动了两个周期,处于平衡位置向上振动,故可根据波形图推断D处于波峰,在t?=?15s时刻a、d之间有两个波谷,C正确;
D.波从c传到d的时间为t=xv=164s=4s,故d在14s时开始起振,在15?s时处于波峰,开始向下振动,D错误;?
故选:ABC.
三、计算题
一列简谐横波图象如下图所示,t1时刻的波形如图中实线所示,t2时刻的波形如图中虚线所示,已知Δt=t2-t1=0.5s,问:
(1)这列波的可能波速的表达式?
(2)若波向左传播,且3T<Δt<4T,波速多大?
(3)若波速ν=68m/s,则波向哪个方向传播?
【答案】解:(1)若波向右传播,根据波形的周期性,v=xt=(8n+2)0.5m/s=16n+4m/s(n=0,1,2,?)?①
同理可得,若波向左传播,v=16n+12m/s(n=0,1,2,?)?②
(2)若波向左传播,且3T<△t<4T,则由v=16n+12m/s
得:v=16×3+12m/s=60m/s
(3)假设波向右传播,将v=68m/s
代入?①得,68=16n+4,n=4,假设成立,故波向右传播
答:(1)这列波的可能波速的表达式为:v=16n+4m/s或v=16n+12m/s(n=0,1,2,?);
(2)若波向左传播,且3T<△t<4T,波速60m/s;
(3)若波速v=68m/s,则波向右传播
【解析】略
如图是某横波的波形图,实线表示某时刻的波形,虚线表示0.2s后的波形图.
(1)若波向左传播,则它传播的可能距离是多少?
(2)若波向右传播,则它的最大周期是多少?
(3)若波速为35m/s,则波的传播方向如何?
【答案】解:(1)若向左传播,Δt时间内波传播的距离为Δx=(n+34)λ? (n=0,1,2…)
其中λ=4m
得到x=(4n+3)m,(n=0,1,2…),
可能距离为3m、7m、11m…
(2)当波向右传播时,和周期T的关系为
1,2…)
所以T=0.84n+1s(n=0,1,2…)
当n=0时,T有最大值Tmax=0.80+1s=0.8s
(3)波在内传播的距离为
结合图形可判断出波是向左传播的。
【解析】(1)波形的平移法可知,波向左传播的最小距离等于34波长,由波的周期性,写出波传播的可能距离;
(2)当波向右传播时,写出和周期T的关系,得到周期的通式,求解最大周期;
(3)由△x=vt求出波传播的距离,由波形的平移法确定波的传播方向。
本题知道两个时刻的波形,要根据波的周期性和双向性进行研究,往往会得到波传播距离和周期的通项,再得到特殊值。
一列简谐横波在t=13s的波形图如图(a)所示,P、Q是介质中的两个质点,图(b)是质点Q的振动图象。求:
(i)波速及波的传播方向;
(ii)质点Q的平衡位置的x坐标。
【答案】解:(i)由图(a)可以看出,该波的波长为λ=36cm,
由图(b)可以看出周期T=2s,
故波速为v=λT=18cm/s,
由(b)可知,当t=13s时,Q向上振动,结合图(a)可知,该波沿x轴负方向传播;
(ii)设质点P、Q的平衡位置的x轴坐标分别为xP、xQ,由图(a)可知,x=0处y=-A2=Asin(-30°)
因此xP=30°360?λ=3cm
由图(b)可知,在t=0时Q点处于平衡位置,经过△t=13s,其振动状态向x轴负方向传播到P点处,
所以xQ-xP=v△t=6cm,
解得质点Q的平衡位置的x坐标为xQ=9cm。
【解析】(i)由图(a)得到波长,由图(b)得到周期,根据v=λT计算波速,根据振动情况确定传播方向;
(ii)首先确定P点平衡位置横坐标,再根据向x轴负方向传播到P点处经过的时间,由此求出质点Q的平衡位置的x坐标。
本题主要是考查了波的图象;解答本题关键是要掌握振动的一般方程y=Asinωt,知道方程中各字母表示的物理意义,能够根据图象直接读出振幅、波长和各个位置处的质点振动方向,知道波速、波长和频率之间的关系。
如图所示,图甲是一列简谐横波在t=0时刻的波形图,P点是此时处在平衡位置的一个质点.图乙是质点P的振动图象.
(1)判断这列波的传播方向;
(2)经过时间t1=6s,质点P通过的路程s;
(3)经过t2=30s,波向前传播的距离x.
【答案】解:(1)由图乙知,t=0时刻质点P正向上振动,所以根据波形平移法知,该波沿x轴正方向传播;
(2)从图乙可知振动周期为T=4s,一个周期内质点通过的路程为4A,则经过时间t1=6s=1.5T,质点P通过的路程为:s=1.5×4A=6×2cm=12cm;
(3)波速为:v=λT=84m/s=2m/s。
经过t2=30s,波向前传播的距离x=vt2=2×30m=40m。
答:(1)这列波的传播方向沿x轴正方向;
(2)经过时间t1=6s,质点P通过的路程s是12cm;
(3)经过t2=30s,波向前传播的距离x是60m。
【解析】本题的关键要把握振动图象和波动图象的内在联系.要注意两种图象判断质点振动方向方法的区别,波动图象常用波形平移法判断质点的振动方向.而振动图象常用斜率分析质点的振动方向。
(1)根据振动图象判断出t=0时刻P点的振动方向,再判断波的传播方向;
(2)图乙读出周期,由周期与时间的关系,结合题意,即可求解P点通过的路程;
(3)由公式v=λT求出波速,由x=vt求解波传播的距离。
四、综合题
(1)一简谐机械横波沿x轴负方向传播,已知波的波长为8?m,周期为2?s,t=1?s时刻波形如图甲所示,a、b、d是波上的三个质点。图乙是波上某一点的振动图像。则下列说法正确的是(????)(填正确答案标号。)
A.图乙可以表示d质点的振动
B.图乙可以表示b质点的振动
C.a、b两质点在t=1.5?s时速度大小相同
D.该波传播速度为v=4?m/s
E.t=0时b质点速度沿y轴正方向
(2)如图中实线是一列简谐横波在t1=0时刻的波形,虚线是这列波在t2=0.5?s时刻的波形。
(1)写出这列波的波速表达式;
(2)若波速大小为74?m/s,波速方向如何?
【答案】(1)?ADE;
(2)解:(1)由题图图像可知λ=8?m?
当波向右传播时,波传播距离为
s=nλ+38λ=(8n+3)m(n=0,1,2…)
波速为v=sΔt=8n+30.5?m/s=(16n+6)?m/s(n=0,1,2…)。?
当波向左传播时,波传播距离为
s=nλ+58λ=(8n+5)?m(n=0,1,2…)?
波速为v=sΔt=8n+50.5?m/s=(16n+10)m/s(n=0,1,2…)。?
(2)若波速大小为74?m/s,在Δt=t2-t1时间内波传播的距离为s=v·Δt=74×0.5?m=37?m。?
因为37?m=4λ+58λ,所以波向左传播。?
【解析】
(1)
【分析】
本题既要能理解振动图象和波动图象各自的物理意义,又要抓住它们之间内在联系,能熟练根据波的传播方向判断出质点的速度方向。
质点的速度和加速度可根据质点的位置进行判断。在平衡位置时,速度最大,加速度最小;在最大位移处,速度为零,加速度最大。根据图乙中t=0时刻质点的位置和振动方向,在图甲上找出对应的质点;再根据波长、周期和频率的关系即可确定传播速度,根据带动法确定各质点的振动方向。
【解答】
AB.由图乙知,t=1s时刻质点经过平衡位置向上运动,图甲是t=1s时刻的波形,此时a位于波峰,位移最大,与图乙中t=1s时刻质点的状态不符,而质点b在t=1s时刻经过平衡位置向下运动,与图乙中t=1时刻质点的状态不符,而质点d在t=1s时刻经过平衡位置向上运动,所以图乙不能表示质点b的振动,可以表示质点d的振动,故 A正确, B错误。
C.ab两质点相差四分之一个周期,t=1.5s,则△t=0.5s=0.25T时,质点a位于平衡位置,质点b处于波谷,速度大小不可能相等,故 C错误。
D.波的波长为8m,周期为2s,故传播速度v=λT=82m/s=4m/s,故D正确;
E.根据平移法可知,t=0时b点速度沿y轴正方向,故 E正确。
故选ADE。
(2)
本题考查了波传播的多解性,分情况讨论。
(1)波传播存在两种可能,向左或向右传播,根据题干信息,?利用波速公式求解。
(2)由s=vt求出波传播的距离,分析与波长的关系,确定波传播的方向。
(1)图(a)为一列简谐横波在t=2s时的波形图,图(b)为介质中平衡位置在x=2.5m处的质点的振动图象,P是平衡位置为x=1m的质点,下列说法正确的是_________.
A.波速为0.5m/s
B.波的传播方向向左
C.0~1.5s,P运动的路程为6cm
D.3s~5s,P振动方向发生变化
E.t=9s时,P的加速度恰好为零
(2)如图所示,直角玻璃三棱镜置于空气中,已知∠A=60°,∠C=90°,一束极细的光于AC的中点D垂直AC面入射,棱镜的折射率为n=2。
①求此玻璃对空气的临界角;
②光从棱镜第一次射入空气时的折射角。
【答案】(1)ADE;
(2)解:①设玻璃对空气的临界角为C,则sinC=1n=12???
所以
②如图所示因为i1=60°>C,所以光线在AB面上将发生全反射
由几何知识得?i2=i1-30°=30°
【解析】
(1)【分析】
先根据质点的振动图象,判断波的传播方向,再根据波长和周期求波速;据波形成的条件和特点分析各质点的振动情况。
本题考查了横波的图像,波长、频率和波速的关系;熟练利用波形平移法判断质点的振动方向与传播方向、利用周期表示时间,求质点的路程、注意时间和空间周期性的对应。
【解答】
A.由图(a)可知该简谐横波波长为2m,由图(b)知周期为4s,则波速为v=λT=0.5m/s,故A正确;
B.根据图(b)的振动图象可知,在x=2.5m处的质点在t=2s时振动方向向下,由同侧法可知该波向右传播,故B错误;
C.由波的平移法可知,0时刻P质点位移波谷,从此位置开始经过1.5s即八分之三周期,则P运动的路程大于6cm,故C错误;
D.t=2s时P质点位于波峰,经过四分之一周期即1s后,P质点向下运动到平衡位置,再经过1s,P质点向下运动位于波谷,接着反向向上振动,故D正确;
E.从图(a)所示再经过9s,即经过214T,质点P恰好经过平衡位置,则此时的加速度为0,故E正确。
故选ADE。
(2)本题考查了光的折射和光的全反射,光学问题分析计算的关键是正确的画出光路图。
①根据临界角公式计算玻璃对空气的临界角;
②根据光路图结合临界角分析光从哪个面第一次射入空气,根据几何关系结合折射定律计算折射角。
(1)如图为一列传播速率v=8m/s的简谐横波在t=0时刻的波形图,P是平衡位置为x1=3.5m处的质点,Q是平衡位置为x2=26m处的质点,此时质点P正做减速运动,则(????)
A. 该波沿x轴负方向传播
B.t=2.5s时,Q质点开始振动
C.Q质点的起振方向沿y轴正向
D.t=2.7s时质点Q向y轴正方向加速运动
E.?1s内质点P通过的路程为40 cm
(2)如图所示,小玻璃球的半径为R,折射率n=3,今有一束细光束从与直径相距d=32R的点,沿直径方向照在小玻璃球上,入射光线可经过折射、反射、折射,再射出后恰能平行于原射入方向返回。已知光在真空中的传播速度为c,求该细光束在玻璃球中的传播时间。
center0
【答案】(1)BCE
(2)解:画出光路图如图,设入射点C对应的入射角为θ1,折射角为θ2,
由几何关系可得sinθ1=dR=32,所以θ1=60?
由折射定律sinθ1sinθ2=n得:θ2=30?
所以BC长l=2Rcosθ2=3R??
由对称性可知总路程为x=2l=4Rcosθ2=23R??
设玻璃球中的光速为v,由n=cv得v=c3????
所以传播时间t=xv=6Rc??
【解析】
(1)【分析】
由题图可读出振幅A,波长,由?T=λv可得周期,由质点P正做减速运动,据质点振动方向和波的传播方向的关系可知该波的传播方向,分析周期与t=2.5s的关系,判断t=2.7s时质点Q的振动方向,1s内质点P通过的路程为振幅的8倍。
【解答】
A.由质点P正做减速运动可知t=0时刻P向下运动,据质点振动方向和波的传播方向的关系可知该波沿x轴正方向传播,A错误。
BD.经过2.5s时间,Q点开始振动,?T4<0.2s
E.由题图可读出振幅A=5cm,波长λ=4m,由?T=λv可得周期为0.5s,1s内,即两个周期内,质点P通过的路程为振幅的8倍,即40cm,E正确。
故选BCE。
(2)画出光路图,由几何知识和折射定律求出光线在玻璃中的传播距离,由t=xv
进而可求出时间。本题考查了折射定律的应用,正确作出光路图,灵活运用几何知识求解是关键。
(1)一列简谐横波在同种均匀介质中传播,某时刻波形如图甲所示。由该时刻开始计时,质点L的振动情况如图乙所示。下列说法正确的是(????)
A.该横波沿x轴正方向传播
B.质点N该时刻向y轴正方向运动
C.质点L经半个周期将沿x轴正方向移动
D.该时刻质点K与M的速度、加速度大小都相同
E.从该时刻起,质点O与质点N的振动情况始终相同
(2)如图所示,圆心为O、半径为R的半圆形玻璃砖置于水平面上,当入射角为θ时,光线从玻璃砖P点射入后,直接从圆形表面顶端B点射出,已知OP=2R2,sinθ=63,真空中的光速为c.求:
Ⅰ.玻璃砖的折射率n;
Ⅱ.当光线垂直OP边从P点入射时,光在玻璃中传播所用的时间t。
【答案】(1)ADE;
(2)解:Ⅰ.作出两种情况下的光路图,如图所示
由于sin∠OBP=2R2(2R2)2+R2
在B处射出,故∠OBP=∠BPA
n=sinθsin∠BPA
联立可得n=2
Ⅱ.光在玻璃中的传播速度v
v=cn
当光线垂直OP边从P点入射时:
sin∠OAP=22RR=22????sinC=1n=22
所以∠OAP=C=45°,光线在玻璃中发生全反射,从与P点对称的Q点射出,
t=4?OPv
解得t=4Rc
【解析】
(1)
【分析】
本题要掌握用微平移法判断质点的振动方向和波的传播方向,知道质点不会随波迁移,理解波动图象与振动图象的区别,注意速度与加速度是矢量,是否相同还要考虑其方向。
根据质点L的振动图象,从而判定波的传播方向,再依据波的微平移法,则可确定质点N点的振动方向,波在传播过程中,质点不随波迁移;最后结合速度与加速度是矢量,是否相等要从大小与方向两角度考虑。
【解答】
A.由图乙可知,质点L在该时刻,向y轴正方向振动,依据微平移法,可知,该横波沿x轴正方向传播,故A正确;
B.由上分析,结合微平移法,可知,质点N该时刻向y轴负方向运动,故B错误;
C.依据机械波在传播过程中质点并不随波一起迁移,因此质点L经半个周期不会沿x轴正方向移动到N点,故C错误;
D.因K、M之间间隔半个波长,K、M的步调始终相反,因此该时刻质点K与M的速度、加速度大小都相同,但它们的方向不同,故D正确;
E.由图知质点O与质点N间隔一个波长,所以质点O与质点N的振动情况始终相同,故E正确。
故选ADE。
(2)
本题主要是考查了光的折射和光的全发射;解答此类题目的关键是弄清楚光的传播情况,画出光路图,根据图中的几何关系,根据光的折射定律、全反射的条件求解。
