人教版数学八年级下册 17.2《勾股定理的逆定理》 勾股定理应用(Word版 含答案)
文档属性
| 名称 | 人教版数学八年级下册 17.2《勾股定理的逆定理》 勾股定理应用(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 661.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 08:45:25 | ||
图片预览



文档简介
17 .2《勾股定理的逆定理及勾股定理的应用》
一、 选择题
1. 下列各组数中,是勾股数的是( )
A.,, B.,,
C.,, D.,,
2. 三边长分别为、、,则下列条件不能判断是直角三角形的是( )
A.=,=,= B.=,=,=
C.=,=,= D.=,=,=
3. 在下列命题中,该命题的逆命题成立的是?? ?
A.线段垂直平分线上的点到这条线段两个端点的距离相等
B.等边三角形是锐角三角形
C.如果两个角是直角,那么它们相等
D.如果两个实数相等,那么它们的平方相等
4. 五根小木棒,其长度分别为,,,,,现将他们摆成两个直角三角形,其中摆放方法正确的是( )
A. B. C. D.
?5. 如图所示,有一个长、宽各米,高为米且封闭的长方体纸盒,一只昆虫从顶点要爬到顶点,那么这只昆虫爬行的最短路程为()
A.米 B.米 C.米 D.米
?
6. 如图,将一根长的筷子,置于底面半径为,高为的圆柱形水杯中,设筷子露在杯子外面的长度为,则的取值范围是??
A. B.
C. D.
二、 填空题
7. “等腰三角形的两底角相等”的逆命题是________.
8. 在一次游戏中,小丽问小颖“如果我现在从你所站的位置向北走米,后向西走米,再向北走米,那么我与你相距________米.”
9. 如图,中,是边上的一点,,,,,那么的面积是________.
10. 一个三角形三边满足,则这个三角形是________三角形.
11. 如图所示的网格是正方形网格,则________(点是网格线交点).
12. 在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”这个数学问题的意思是说:“有一个水池,水面是一个边长为丈(丈=尺)的正方形,在水池正中央长有一根芦苇,芦苇露出水面??尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各是多少?”设这个水池的深度是尺,根据题意,可列方程为________.
三、 解答题?
13. 已知、、是的三边,且满足,且=,请你探索的形状.
?
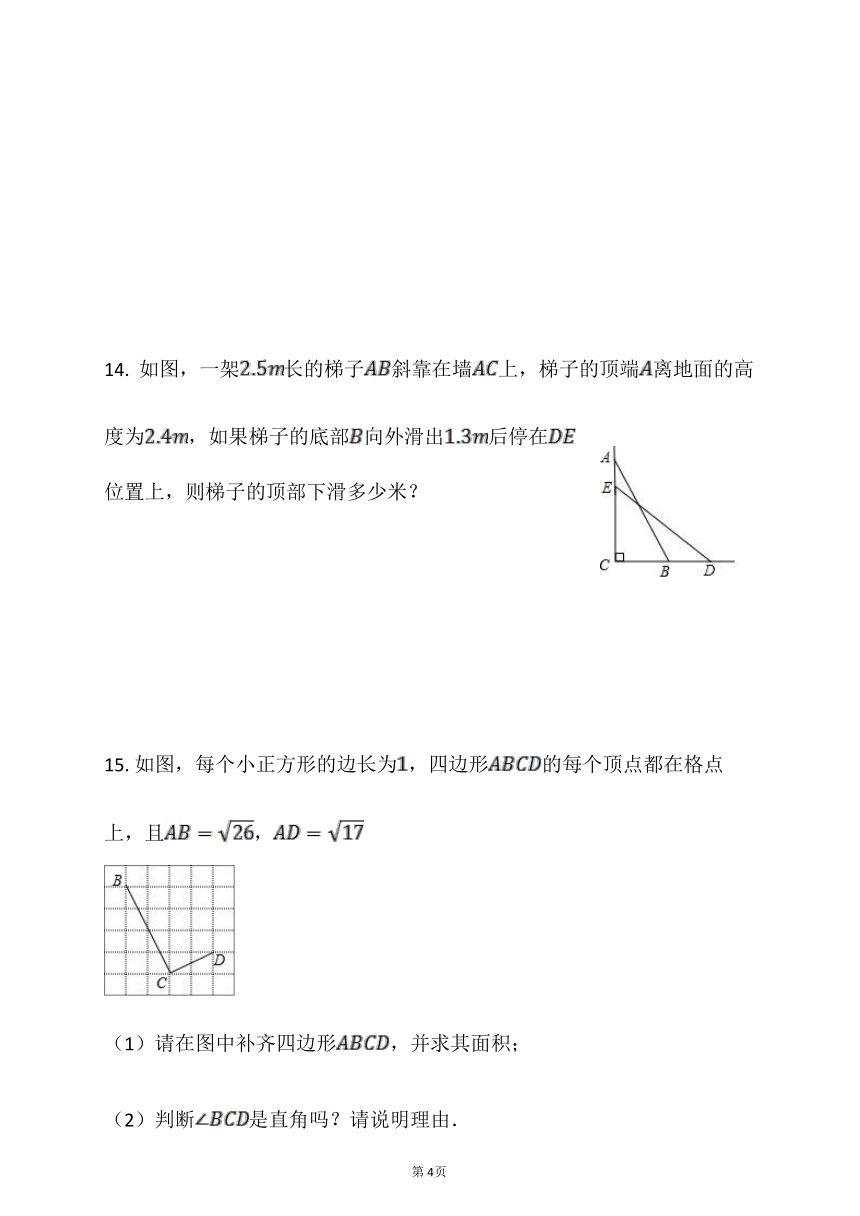
14. 如图,一架长的梯子斜靠在墙上,梯子的顶端离地面的高度为,如果梯子的底部向外滑出后停在位置上,则梯子的顶部下滑多少米?
?
15. 如图,每个小正方形的边长为,四边形的每个顶点都在格点上,且,
(1)请在图中补齐四边形,并求其面积;
(2)判断是直角吗?请说明理由.
?
16. 如图,飞机在空中水平飞行,某一时刻刚好飞到一男孩子头顶上方米处,过了秒,飞机距离这个男孩头顶米.飞机每小时飞行多少千米?
参考答案
17 .2《勾股定理的逆定理及勾股定理的应用》
一、 选择题
1.【答案】A
2.【答案】B
3.【答案】A
4.【答案】D
5.【答案】C
6.【答案】C
二、 填空题
7.【答案】两个角相等的三角形是等腰三角形
8.【答案】
9.【答案】
10.【答案】直角
11.【答案】
12.【答案】
=
三、 解答题
13.【答案】
令.
∴ =,=,=,
∴ =,=,=.
又∵ =,
∴ =,
∴ =.
∴ =,=,=.
∴ 是直角三角形.
14.【答案】
梯子的顶部下滑米
15.【答案】
=
=;
∵ ==,==,==,
∴ =,
∴ =.
16.【答案】
飞机每小时飞行千米.
第8 88页
第7 77页
一、 选择题
1. 下列各组数中,是勾股数的是( )
A.,, B.,,
C.,, D.,,
2. 三边长分别为、、,则下列条件不能判断是直角三角形的是( )
A.=,=,= B.=,=,=
C.=,=,= D.=,=,=
3. 在下列命题中,该命题的逆命题成立的是?? ?
A.线段垂直平分线上的点到这条线段两个端点的距离相等
B.等边三角形是锐角三角形
C.如果两个角是直角,那么它们相等
D.如果两个实数相等,那么它们的平方相等
4. 五根小木棒,其长度分别为,,,,,现将他们摆成两个直角三角形,其中摆放方法正确的是( )
A. B. C. D.
?5. 如图所示,有一个长、宽各米,高为米且封闭的长方体纸盒,一只昆虫从顶点要爬到顶点,那么这只昆虫爬行的最短路程为()
A.米 B.米 C.米 D.米
?
6. 如图,将一根长的筷子,置于底面半径为,高为的圆柱形水杯中,设筷子露在杯子外面的长度为,则的取值范围是??
A. B.
C. D.
二、 填空题
7. “等腰三角形的两底角相等”的逆命题是________.
8. 在一次游戏中,小丽问小颖“如果我现在从你所站的位置向北走米,后向西走米,再向北走米,那么我与你相距________米.”
9. 如图,中,是边上的一点,,,,,那么的面积是________.
10. 一个三角形三边满足,则这个三角形是________三角形.
11. 如图所示的网格是正方形网格,则________(点是网格线交点).
12. 在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”这个数学问题的意思是说:“有一个水池,水面是一个边长为丈(丈=尺)的正方形,在水池正中央长有一根芦苇,芦苇露出水面??尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各是多少?”设这个水池的深度是尺,根据题意,可列方程为________.
三、 解答题?
13. 已知、、是的三边,且满足,且=,请你探索的形状.
?
14. 如图,一架长的梯子斜靠在墙上,梯子的顶端离地面的高度为,如果梯子的底部向外滑出后停在位置上,则梯子的顶部下滑多少米?
?
15. 如图,每个小正方形的边长为,四边形的每个顶点都在格点上,且,
(1)请在图中补齐四边形,并求其面积;
(2)判断是直角吗?请说明理由.
?
16. 如图,飞机在空中水平飞行,某一时刻刚好飞到一男孩子头顶上方米处,过了秒,飞机距离这个男孩头顶米.飞机每小时飞行多少千米?
参考答案
17 .2《勾股定理的逆定理及勾股定理的应用》
一、 选择题
1.【答案】A
2.【答案】B
3.【答案】A
4.【答案】D
5.【答案】C
6.【答案】C
二、 填空题
7.【答案】两个角相等的三角形是等腰三角形
8.【答案】
9.【答案】
10.【答案】直角
11.【答案】
12.【答案】
=
三、 解答题
13.【答案】
令.
∴ =,=,=,
∴ =,=,=.
又∵ =,
∴ =,
∴ =.
∴ =,=,=.
∴ 是直角三角形.
14.【答案】
梯子的顶部下滑米
15.【答案】
=
=;
∵ ==,==,==,
∴ =,
∴ =.
16.【答案】
飞机每小时飞行千米.
第8 88页
第7 77页
