上海市普陀区2011学年第一学期第二次数学月考试题及答案
文档属性
| 名称 | 上海市普陀区2011学年第一学期第二次数学月考试题及答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 100.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-12 00:00:00 | ||
图片预览


文档简介
上海市普陀区2011—2012学年第一学期
九年级数学第二次月考试卷 2011.11.29
(考试时间:100分钟 满分:150分)
题号 一 二 三 总分
19 20 21 22 23 24 25
得分
一、选择题(每题4分,满分24分)
1、函数(为常数)是二次函数的条件为 ( )
(A) (B) (C) (D)
2、把抛物线先向左平移1个单位长度,然后再向上平移3个单位长度,那么平移后的抛物线的解析式是 ( )
(A) (B)
(C) (D)
3、如果二次函数的图像顶点为(1,-3),那么b 和C 的值
是( )
(A) (B)
(C) (D)
4、如图,H是□ABCD的边AD上一点,且,
BH与AC相交于点K,那么AK:KC等于( )
(A)1:1 (B)1:2
(C)1:3 (D)2:3
5、已知△ABC中,∠C=90°,BC=2, ,那么AC的长是( )
(A) (B)3 (C) (D)
6、如图,△ABC中,DE∥BC,BE与CD相交于点F。
如果DF:FC=1:3,那么等于( )
(A)1: (B)1 : 3
(C)1 : 9 (D)1: 18
二、填空题(每题4分,满分48分)
7、二次函数的图像是 。
8、当m 时,关于的函数是二次函数。
9、如果关于的二次函数的图像经过原点,那么m= 。 10、抛物线的顶点在轴上,那么= 。
11、有人说:“二次函数的图像一定与轴相交,并且总有一个交点。”这个判断是否正确?答: 。(填“正确”或“错误”)
12、某公司七月份产值为100万元,设第三季度每个月产值的增长率相同,都为(>0),九月份的产值为万元,那么关于的函数解析式是 。
13、计算:+= 。
14、已知,那么 。(其中为锐角)
15、计算: 。
16、已知点P是线段AB的黄金分割点,且AP>PB。如果AP的长为2,那么PB·AB的值是 。
17、△ABC中,AD是边BC上的高,如果AD2=BD·DC ,那么△ABC是 三角形(按角分类)。
18、如图,□ABCD中,AB=4,AD=6,∠ABC=60°,点P是射线AD上的一个动点(与点A不重合),BP与AC相交于点E。设AP=,当= 时,△ABP与△EBC相似。
三、解答题(第19~22题各10分,第23、24题各12分,第25题14分,满分78分)
19.计算:
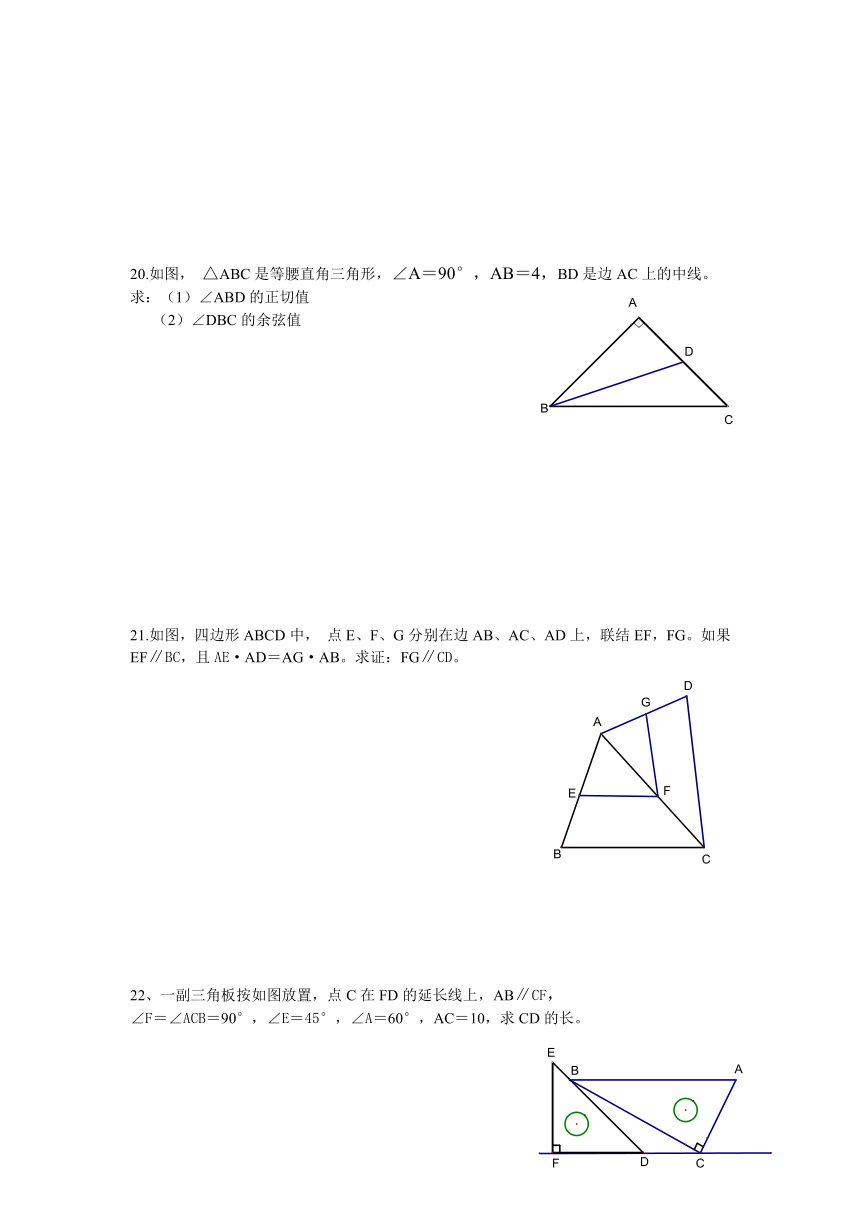
20.如图, △ABC是等腰直角三角形,∠A=90°,AB=4,BD是边AC上的中线。
求:(1)∠ABD的正切值
(2)∠DBC的余弦值
21.如图,四边形ABCD中, 点E、F、G分别在边AB、AC、AD上,联结EF,FG。如果EF∥BC,且AE·AD=AG·AB。求证:FG∥CD。
22、一副三角板按如图放置,点C在FD的延长线上,AB∥CF,
∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,求CD的长。
23、已知抛物线。
(1)把抛物线的表达式化为的形式是 ;
(2)抛物线的开口方向是 ;对称轴是 ;
顶点坐标是 ,它是抛物线的最 点;(填“高”或“低”)
(3)当 时,抛物线是上升的;当 时,抛物线是下降的;
(4)抛物线的值的变化范围是 。
24、如图,某轮船沿正北方向航行,在点A处测得灯塔C在北偏西30°处。轮船以每小时20海里的速度航行,2小时到达点B后,测得灯塔C在轮船北偏西75°处。当该轮船继续航行到达灯塔C的正东方向时,求此时轮船与灯塔C之间的距离。
(结果精确到0.1海里,参考数据:)
25、如图,已知抛物线C1的顶点坐标是D(1,4),且经过点C(2,3),又与轴交于点A、E(点A在点E左边),与轴交于点B。
(1)抛物线C1的表达式是 ;
(2)四边形ABDE的面积等于 ;
(3)问:△AOB与△DBE相似吗?并说明你的理由;
(4)设抛物线C1的对称轴与轴交于点F。另一条抛物线C2经过点E(C2与C1不重合),且顶点为M(a,b),对称轴与轴交于点G,并且以M、G、E为顶点的三角形与以点D、E、F为顶点的三角形全等,求a 、b的值。(只需写出结果,不必写解答过程)。
2011学年九年级(上)数学第二次月考试卷
(考试时间:100分钟 满分:150分)
参考答案与评分标准
一、选择题(每题4分,满分24分)
1.D; 2.D; 3.B; 4.C; 5.A; 6.C.
二、填空题(每题4分,满分48分)
7. 抛物线;8. ;9. 1;10. ;11. 正确;
12. 或;13. 1; 14. QUOTE EMBED Equation.DSMT4 ;15. ;
16.4;17. 直角三角形或钝角三角形;18. 8.
三、解答题(第19~22题各10分,第23、24题各12分,第25题14分,满分78分)
19.解:原始= ………………… 6’ (每个三角比值各1分)
= ………………… 2’
= ………………… 2’
20.解:(1)Rt△ABD中,∠A=90°AD=2,AB=4 ………………………… 1’
………………………… 2’
(2)作DE⊥BC于点E ………………………… 1’
求出 ………………………… 2’
求出 ………………………… 2’
………………………… 2’
21. 证明: ………………………… 1’
………………………… 2’
在△ABC中,∵ EF∥BC ………………………… 1’
………………………… 2’
………………………… 2’
∴ FG ∥ CD ………………………… 2’
22、解:作AM⊥FC,BN⊥FC,垂足为M,N …………………各1’,共 2’
Rt△ACB中, ………………………… 1’
MN=AB=20 ………………………… 1’
Rt△ACM中, ∠ACM=60° AM=10sin60°= ………… 1’
CM=10cos60°=5 …………………… 1’
Rt△BND中,ND=BN=AM= …………………… 2’
∴ DC=MN-ND-CM=20--5=15- …………………… 2’
(其它解法相应给分)
23、解:(1) …………………… 3’
(2)开口向下 ………… 1’ 直线 ………… 1’
顶点坐标(-3,8) ………… 1’ 高 ………… 1’
(3)x < -3 ………… 1’ x > - 3 …… 1’
(4)y ≤8 ………… 3’
24、解:作BD⊥AC于点D ………… 1’
作CE⊥AB于点E ………… 1’
AB=40海里 ………… 1’
BD=40sin30°=20 ………… 1’
AD=40cos30°= ………… 1’
△CDB为等腰直角三角形 ……………… 1’
CD=BD=20 ………… 1’
Rt△ACE中,∠CAE=30° AC=20+………… 1’
∴ ………… 2’
27.3(海里) ………… 1’
答:(略) ………… 1’
25、解:(1)(或) ………… 2’
(2) ………… 2’
(3)相似 ………… 1’
证出: ………… 1’
∴ △AOB∽△DBE ………… 1’
(4)
………………各1’,共7’
九年级数学第二次月考试卷 2011.11.29
(考试时间:100分钟 满分:150分)
题号 一 二 三 总分
19 20 21 22 23 24 25
得分
一、选择题(每题4分,满分24分)
1、函数(为常数)是二次函数的条件为 ( )
(A) (B) (C) (D)
2、把抛物线先向左平移1个单位长度,然后再向上平移3个单位长度,那么平移后的抛物线的解析式是 ( )
(A) (B)
(C) (D)
3、如果二次函数的图像顶点为(1,-3),那么b 和C 的值
是( )
(A) (B)
(C) (D)
4、如图,H是□ABCD的边AD上一点,且,
BH与AC相交于点K,那么AK:KC等于( )
(A)1:1 (B)1:2
(C)1:3 (D)2:3
5、已知△ABC中,∠C=90°,BC=2, ,那么AC的长是( )
(A) (B)3 (C) (D)
6、如图,△ABC中,DE∥BC,BE与CD相交于点F。
如果DF:FC=1:3,那么等于( )
(A)1: (B)1 : 3
(C)1 : 9 (D)1: 18
二、填空题(每题4分,满分48分)
7、二次函数的图像是 。
8、当m 时,关于的函数是二次函数。
9、如果关于的二次函数的图像经过原点,那么m= 。 10、抛物线的顶点在轴上,那么= 。
11、有人说:“二次函数的图像一定与轴相交,并且总有一个交点。”这个判断是否正确?答: 。(填“正确”或“错误”)
12、某公司七月份产值为100万元,设第三季度每个月产值的增长率相同,都为(>0),九月份的产值为万元,那么关于的函数解析式是 。
13、计算:+= 。
14、已知,那么 。(其中为锐角)
15、计算: 。
16、已知点P是线段AB的黄金分割点,且AP>PB。如果AP的长为2,那么PB·AB的值是 。
17、△ABC中,AD是边BC上的高,如果AD2=BD·DC ,那么△ABC是 三角形(按角分类)。
18、如图,□ABCD中,AB=4,AD=6,∠ABC=60°,点P是射线AD上的一个动点(与点A不重合),BP与AC相交于点E。设AP=,当= 时,△ABP与△EBC相似。
三、解答题(第19~22题各10分,第23、24题各12分,第25题14分,满分78分)
19.计算:
20.如图, △ABC是等腰直角三角形,∠A=90°,AB=4,BD是边AC上的中线。
求:(1)∠ABD的正切值
(2)∠DBC的余弦值
21.如图,四边形ABCD中, 点E、F、G分别在边AB、AC、AD上,联结EF,FG。如果EF∥BC,且AE·AD=AG·AB。求证:FG∥CD。
22、一副三角板按如图放置,点C在FD的延长线上,AB∥CF,
∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,求CD的长。
23、已知抛物线。
(1)把抛物线的表达式化为的形式是 ;
(2)抛物线的开口方向是 ;对称轴是 ;
顶点坐标是 ,它是抛物线的最 点;(填“高”或“低”)
(3)当 时,抛物线是上升的;当 时,抛物线是下降的;
(4)抛物线的值的变化范围是 。
24、如图,某轮船沿正北方向航行,在点A处测得灯塔C在北偏西30°处。轮船以每小时20海里的速度航行,2小时到达点B后,测得灯塔C在轮船北偏西75°处。当该轮船继续航行到达灯塔C的正东方向时,求此时轮船与灯塔C之间的距离。
(结果精确到0.1海里,参考数据:)
25、如图,已知抛物线C1的顶点坐标是D(1,4),且经过点C(2,3),又与轴交于点A、E(点A在点E左边),与轴交于点B。
(1)抛物线C1的表达式是 ;
(2)四边形ABDE的面积等于 ;
(3)问:△AOB与△DBE相似吗?并说明你的理由;
(4)设抛物线C1的对称轴与轴交于点F。另一条抛物线C2经过点E(C2与C1不重合),且顶点为M(a,b),对称轴与轴交于点G,并且以M、G、E为顶点的三角形与以点D、E、F为顶点的三角形全等,求a 、b的值。(只需写出结果,不必写解答过程)。
2011学年九年级(上)数学第二次月考试卷
(考试时间:100分钟 满分:150分)
参考答案与评分标准
一、选择题(每题4分,满分24分)
1.D; 2.D; 3.B; 4.C; 5.A; 6.C.
二、填空题(每题4分,满分48分)
7. 抛物线;8. ;9. 1;10. ;11. 正确;
12. 或;13. 1; 14. QUOTE EMBED Equation.DSMT4 ;15. ;
16.4;17. 直角三角形或钝角三角形;18. 8.
三、解答题(第19~22题各10分,第23、24题各12分,第25题14分,满分78分)
19.解:原始= ………………… 6’ (每个三角比值各1分)
= ………………… 2’
= ………………… 2’
20.解:(1)Rt△ABD中,∠A=90°AD=2,AB=4 ………………………… 1’
………………………… 2’
(2)作DE⊥BC于点E ………………………… 1’
求出 ………………………… 2’
求出 ………………………… 2’
………………………… 2’
21. 证明: ………………………… 1’
………………………… 2’
在△ABC中,∵ EF∥BC ………………………… 1’
………………………… 2’
………………………… 2’
∴ FG ∥ CD ………………………… 2’
22、解:作AM⊥FC,BN⊥FC,垂足为M,N …………………各1’,共 2’
Rt△ACB中, ………………………… 1’
MN=AB=20 ………………………… 1’
Rt△ACM中, ∠ACM=60° AM=10sin60°= ………… 1’
CM=10cos60°=5 …………………… 1’
Rt△BND中,ND=BN=AM= …………………… 2’
∴ DC=MN-ND-CM=20--5=15- …………………… 2’
(其它解法相应给分)
23、解:(1) …………………… 3’
(2)开口向下 ………… 1’ 直线 ………… 1’
顶点坐标(-3,8) ………… 1’ 高 ………… 1’
(3)x < -3 ………… 1’ x > - 3 …… 1’
(4)y ≤8 ………… 3’
24、解:作BD⊥AC于点D ………… 1’
作CE⊥AB于点E ………… 1’
AB=40海里 ………… 1’
BD=40sin30°=20 ………… 1’
AD=40cos30°= ………… 1’
△CDB为等腰直角三角形 ……………… 1’
CD=BD=20 ………… 1’
Rt△ACE中,∠CAE=30° AC=20+………… 1’
∴ ………… 2’
27.3(海里) ………… 1’
答:(略) ………… 1’
25、解:(1)(或) ………… 2’
(2) ………… 2’
(3)相似 ………… 1’
证出: ………… 1’
∴ △AOB∽△DBE ………… 1’
(4)
………………各1’,共7’
同课章节目录
