人教版七年级数学 下册 第七章 7.2.2 用坐标表示平移 课件(共39张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第七章 7.2.2 用坐标表示平移 课件(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 00:00:00 | ||
图片预览









文档简介
(共39张PPT)
温故知新
1.什么是平面直角坐标系?
2.如何利用平面直角坐标系表示地理位置?
3.什么叫平移?平移后得到的图形与原图形的关系?
1、利用平面直角坐标系表示地理位置:
(1)建立坐标系,选择一个适当的参照点为原点、确定x轴、
y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点、写出各点的坐标和各个地点的名称.
温故知新
2.
什么叫做平移?
3
.平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
平移后图形只改变位置,形状、大小不变。
温故知新
上节课我们学习了利用平面直角坐标系表示地理位置,平移能不能利用平面直角坐标系来表示呢?
导入新课
7.2.2
用坐标表示平移
人教版七年级数学
下册
掌握坐标变化与图形平移的关系;
能利用点的平移规律将平面图形进行平移;
会根据图形上点的坐标的变化,来判定图形的移动过程。
学习目标
认真阅读课本中7.2.2
用坐标表示平移的内容,完成下面练习并体验知识点的形成过程。
自主研学
思考:你会下象棋吗?如果下一步下“马走日”,你觉得应该走到哪里呢?
目标导学一:平面直角坐标系中点的平移
0
-3
-2
-1
1
2
3
4
x
3
2
1
-2
-1
-3
4
A
(-2,-3)
y
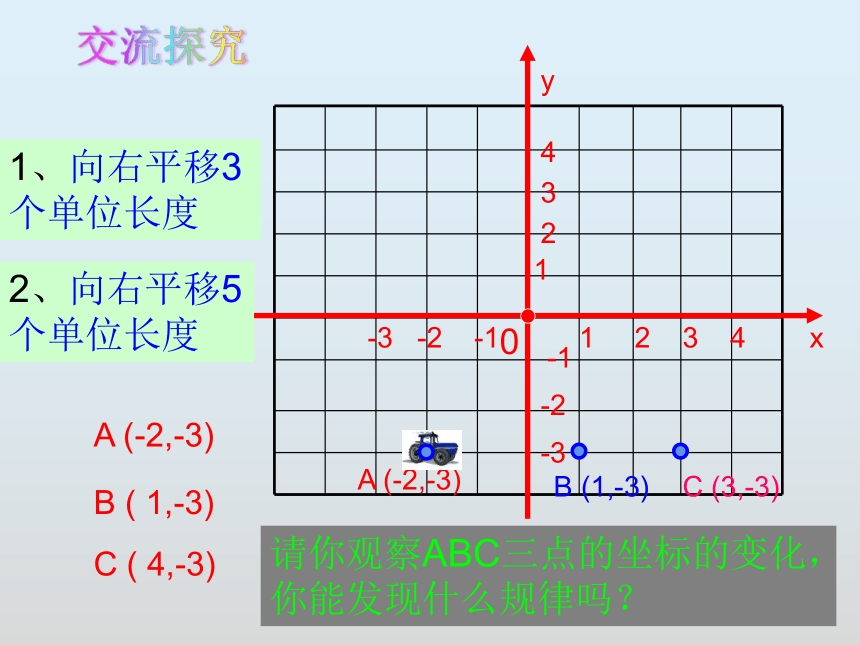
1、向右平移3个单位长度
2、向右平移5个单位长度
B
(1,-3)
C
(3,-3)
A
(-2,-3)
B
(
1,-3)
C
(
4,-3)
请你观察ABC三点的坐标的变化,你能发现什么规律吗?
交流探究
0
-3
-2
-1
1
2
3
4
x
3
2
1
-2
-1
-3
4
A
(-2,-3)
y
C
(-2,4)
B
(-2,2)
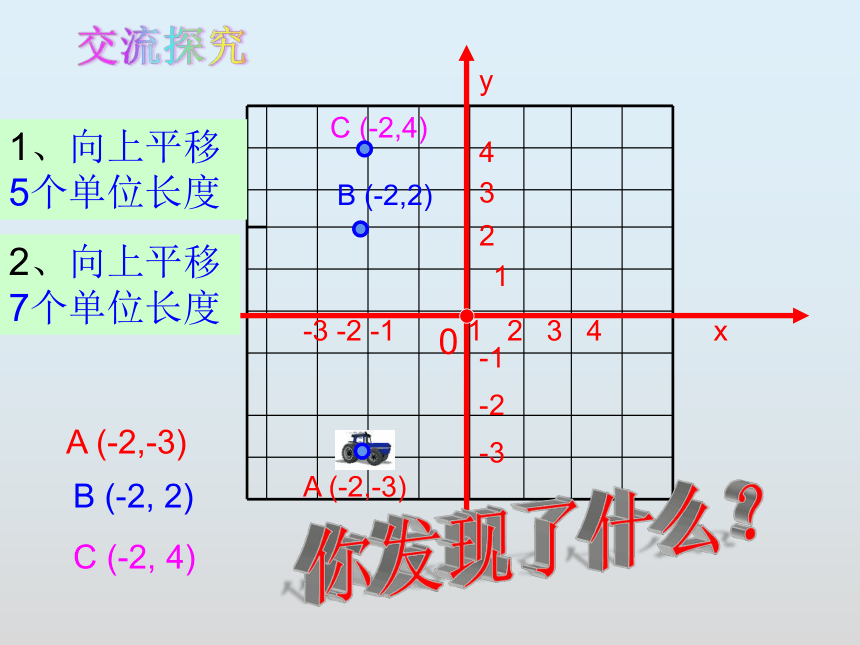
1、向上平移5个单位长度
2、向上平移7个单位长度
A
(-2,-3)
C
(-2,
4)
B
(-2,
2)
你发现了什么?
交流探究
(1)左右平移:
向右平移a个单位
(2)上下平移:
点(x,y)
,
向左平移a个单位
点(x,y)
,
(x+a,y)
(x-a,y)
向上平移b个单位
点(x,y)
,
向下平移b个单位
点(x,y)
,
(x,y+b)
(x,y-b)
点的平移
点(x,y)
,
向右平移a个单位,
向下平移b个单位
(x+a,y-b)
知识归纳
左右平移,纵坐标不变,横坐标变化(左减右加)
上下平移,横坐标不变,纵坐标变化(下减上加)
例1
平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8)
B.(1,-2)
C.(-6,-1)
D.(0,-1)
点的平移变换:左右移动改变点的横坐标,左减右
加;上下移动改变点的纵坐标,下减上加.
总结
C
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
1.
在平面直角坐标系中,有一点P(-4,2),若将点P:
(1)向左平移2个单位长度,所得点的坐标为____________
;
(2)向右平移3个单位长度,所得点的坐标为____________
;
(3)向下平移4个单位长度,所得点的坐标为____________
;
(4)向上平移5个单位长度,所得点的坐标为____________
;
(-6,2)
(-1,2)
(-4,
-2)
(-4,7)
即学即练
2、在平面直角坐标系中,有一点P(-4,2),
(1)若将P先向右平移5个单位长度,再向上平移3个单位长度,所得坐标为_____________
。
(2)若将P先向上平移3个单位长度,再向右平移5个单位长度,所得坐标为_____________。
(1,5)
(1,5)
即学即练
3.在坐标中描出点A(-2,-3)并进行如下平移:
(1)
将点A向右平移a(a>o)个单位长度得到点An,则
点An的坐标是
;
(2)将点A向左平移a(a>o)个单位长度得到点An?,则
点An
?的坐标是
;
(-2-a
,-3)
(-2+
a
,-3)
即学即练
问题1:如图,线段AB的两个端点坐标分别为:A(1,1),B(4,4),
将线段AB向上平移2个单位,作出它的像A′B′,并写出点A′,B′的坐标.
目标导学二:平面直角坐标系中图形的平移
1.
作出线段两个端点平移后的对应点.
2.
连接两个对应点,所得图形即为所求平移图形.
逆向说理
1.
把点M(1,2)平移后得到点N(1,-2)则平移的过程是:
向下平移4个单位
2.
把点M(-3,1)平移后得到点N(-1,4)则平移的过程是:
向右平移2个单位,再向上平移3个单位
或:向上平移3个单位,再向右平移2个单位
线段CD是由线段AB平移得到的。
点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________。
(1,2)
即学即练
3
2
1
-2
-1
-3
4
y
A
B
C
-4
A1
C1
B1
问题:如图,三角形ABC在坐标平面内平移后得到三角形A1B1C1.
1.移动的方向怎样?
2.写出三角形ABC与三角形A1B1C1各点的坐标,它们有怎样的变化?
-3
-2
-1
O
1
2
3
4
x
向右平移5个单位;
A(-1,3),B(-4,2),
C(-2,1),A1(4,3),B1(1,2),C1(3,1);
平移后的对应点的横坐标增加了5,纵坐标不变;
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
(3,4)
(4,1)
A
B
C
A`
B`
C`
(2,2)
(-3,4)
(-2,1)
(-4,2)
将?ABC三个顶点的横坐标都减去6,得到?A’B’C’。它与?
ABC的大小,形状和位置有什么关系?
是由?
ABC向左平移6个单位长度得到
?A’B’C’
将三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是:
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
(-1,4)
(-4,-1)
(1,1)
C
O
1
2
3
4
1
2
3
-1
-2
-3
-4
-1
-2
-3
-4
A
B
C
A1
B2
C1
A2
C2
仔细观察,你定会有所发现!
y
x
B1
将△ABC三个顶点的横坐标都减
6,纵坐标减5,又能得到什么结论?
①
②
探究
总结:图形的斜向平移,
可通过左右平移和上下平移来完成。
2
1
-1
-2
-3
-4
-6
-4
-2
2
4
x
y
1
2
3
4
-
2
1
2
-
1
-
5
-
3
-
1
-
2
0
-
3
-
4
-
4
A
C
B
A
C
B
A
C
B
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
1
2
3
一般地,图形经过两次平移后得到的图形,可以通过原来的图形作一次平移得到.
注意
(1)横变纵不变:
右移a个单位
图形上所有点(x,y)
,
(x+a,y)
图形的平移
左移a个单位
图形上所有点(x,y)
,
(x-a,y)
上移b个单位
图形上所有点(x,y)
,
(x,y+b)
下移b个单位
图形上所有点(x,y)
,
(x,y-b)
(2)纵变横不变:
图形上所有点(x,y),
(x+a,y-b)
右移a个单位,再下移b个单位
知识归纳
如图,将平行四边形ABCD向左平移2个单位长度,然后再向上平移3个单位长度,可以得到平行四边形A′B′C′D′,画出平移后的图形,并指出其各个顶点的坐标.
解:如图所示,四边形A′B′C′D′即为所求作的图形,
各点坐标分别为A′(-3,1)、B′(1,1)、C′(2,4)、
D′(-2,4).
即学即练
例
如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上一点,三角形ABC经平移后点P的对应点为P1(a+6,b+2).
(1)请画出上述平移后的三角
形A1B1C1,并写出点A、C、
A1、C1的坐标;
1
y
O
1
x
A
B
C
A1
B1
C1
解:(1)三角形A1B1C1如图所示,各点的坐标分别为A(-3,2)、C(-2,0)、A1(3,4)、C1(4,2);
P
P1
1
y
O
1
x
A
B
C
A1
B1
C1
(2)
求出以A、C、A1、C1为顶点的四边形的面积.
(2)连接AA1,CC1,
P
P1
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y)
向左平移a个单位
原图形上的点(x,y)
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y)
向下平移b个单位
原图形上的点(x,y)
(x,y+b)
(x,y-b)
图形平移与点的坐标变化间的关系
知识归纳
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
向右平移,横坐标加上一个正数
向左平移,横坐标减去一个正数
横坐标不变
向上平移,纵坐标加上一个正数
向下平移,纵坐标减去一个正数
课堂小结
1.点A`(6,3)是由点A(-2,3)经过____
______________得到的.点B(4,3)向______________得到B`(6,3)
向右平
移8个单位长度
右平移2个单位长度
检测目标
2.将点A(-3,2)向下平移3个单位,再向右平移4个单位得点B,则B点坐标是
3.将点P(0,-2)向左平移2个单位,再向上平移4个单位得点Q(x,y),则xy=
(1,-1)
-4
检测目标
4.点A’(6,3)是由点A(-2,3)向__
平移
单位长度得到的.
点B(4,3)向
平移
单位长度得到B’(6,3)
5、点A(8,9)是向__
平移
单位长度.再向
平移
单位长度得到B(6,3)
右
8个
右
2
左
2
6
下
检测目标
x
Y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
6.有相距5个单位的两点
A(-3,a),B(b,4),
AB//x轴,则a=
___
,b=
___
。
A
B
4
2或-8
检测目标
7.如图△ABC中任意一点P(x,y)经平移后对应点为P1(x+5,y+3),将△ABC作同样的平移到△A1B1C1。求A1、B1、C1的坐标
(2)
(2)
A1(3,6)
B1(1,4)
C1(7,3)
A(-2,3)
B(-4,-1)
C(2,0)
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
温故知新
1.什么是平面直角坐标系?
2.如何利用平面直角坐标系表示地理位置?
3.什么叫平移?平移后得到的图形与原图形的关系?
1、利用平面直角坐标系表示地理位置:
(1)建立坐标系,选择一个适当的参照点为原点、确定x轴、
y轴的正方向;
(2)根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
(3)在坐标平面内画出这些点、写出各点的坐标和各个地点的名称.
温故知新
2.
什么叫做平移?
3
.平移后得到的新图形与原图形有什么关系?
把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。
平移后图形只改变位置,形状、大小不变。
温故知新
上节课我们学习了利用平面直角坐标系表示地理位置,平移能不能利用平面直角坐标系来表示呢?
导入新课
7.2.2
用坐标表示平移
人教版七年级数学
下册
掌握坐标变化与图形平移的关系;
能利用点的平移规律将平面图形进行平移;
会根据图形上点的坐标的变化,来判定图形的移动过程。
学习目标
认真阅读课本中7.2.2
用坐标表示平移的内容,完成下面练习并体验知识点的形成过程。
自主研学
思考:你会下象棋吗?如果下一步下“马走日”,你觉得应该走到哪里呢?
目标导学一:平面直角坐标系中点的平移
0
-3
-2
-1
1
2
3
4
x
3
2
1
-2
-1
-3
4
A
(-2,-3)
y
1、向右平移3个单位长度
2、向右平移5个单位长度
B
(1,-3)
C
(3,-3)
A
(-2,-3)
B
(
1,-3)
C
(
4,-3)
请你观察ABC三点的坐标的变化,你能发现什么规律吗?
交流探究
0
-3
-2
-1
1
2
3
4
x
3
2
1
-2
-1
-3
4
A
(-2,-3)
y
C
(-2,4)
B
(-2,2)
1、向上平移5个单位长度
2、向上平移7个单位长度
A
(-2,-3)
C
(-2,
4)
B
(-2,
2)
你发现了什么?
交流探究
(1)左右平移:
向右平移a个单位
(2)上下平移:
点(x,y)
,
向左平移a个单位
点(x,y)
,
(x+a,y)
(x-a,y)
向上平移b个单位
点(x,y)
,
向下平移b个单位
点(x,y)
,
(x,y+b)
(x,y-b)
点的平移
点(x,y)
,
向右平移a个单位,
向下平移b个单位
(x+a,y-b)
知识归纳
左右平移,纵坐标不变,横坐标变化(左减右加)
上下平移,横坐标不变,纵坐标变化(下减上加)
例1
平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8)
B.(1,-2)
C.(-6,-1)
D.(0,-1)
点的平移变换:左右移动改变点的横坐标,左减右
加;上下移动改变点的纵坐标,下减上加.
总结
C
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
1.
在平面直角坐标系中,有一点P(-4,2),若将点P:
(1)向左平移2个单位长度,所得点的坐标为____________
;
(2)向右平移3个单位长度,所得点的坐标为____________
;
(3)向下平移4个单位长度,所得点的坐标为____________
;
(4)向上平移5个单位长度,所得点的坐标为____________
;
(-6,2)
(-1,2)
(-4,
-2)
(-4,7)
即学即练
2、在平面直角坐标系中,有一点P(-4,2),
(1)若将P先向右平移5个单位长度,再向上平移3个单位长度,所得坐标为_____________
。
(2)若将P先向上平移3个单位长度,再向右平移5个单位长度,所得坐标为_____________。
(1,5)
(1,5)
即学即练
3.在坐标中描出点A(-2,-3)并进行如下平移:
(1)
将点A向右平移a(a>o)个单位长度得到点An,则
点An的坐标是
;
(2)将点A向左平移a(a>o)个单位长度得到点An?,则
点An
?的坐标是
;
(-2-a
,-3)
(-2+
a
,-3)
即学即练
问题1:如图,线段AB的两个端点坐标分别为:A(1,1),B(4,4),
将线段AB向上平移2个单位,作出它的像A′B′,并写出点A′,B′的坐标.
目标导学二:平面直角坐标系中图形的平移
1.
作出线段两个端点平移后的对应点.
2.
连接两个对应点,所得图形即为所求平移图形.
逆向说理
1.
把点M(1,2)平移后得到点N(1,-2)则平移的过程是:
向下平移4个单位
2.
把点M(-3,1)平移后得到点N(-1,4)则平移的过程是:
向右平移2个单位,再向上平移3个单位
或:向上平移3个单位,再向右平移2个单位
线段CD是由线段AB平移得到的。
点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________。
(1,2)
即学即练
3
2
1
-2
-1
-3
4
y
A
B
C
-4
A1
C1
B1
问题:如图,三角形ABC在坐标平面内平移后得到三角形A1B1C1.
1.移动的方向怎样?
2.写出三角形ABC与三角形A1B1C1各点的坐标,它们有怎样的变化?
-3
-2
-1
O
1
2
3
4
x
向右平移5个单位;
A(-1,3),B(-4,2),
C(-2,1),A1(4,3),B1(1,2),C1(3,1);
平移后的对应点的横坐标增加了5,纵坐标不变;
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
(3,4)
(4,1)
A
B
C
A`
B`
C`
(2,2)
(-3,4)
(-2,1)
(-4,2)
将?ABC三个顶点的横坐标都减去6,得到?A’B’C’。它与?
ABC的大小,形状和位置有什么关系?
是由?
ABC向左平移6个单位长度得到
?A’B’C’
将三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是:
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
(-1,4)
(-4,-1)
(1,1)
C
O
1
2
3
4
1
2
3
-1
-2
-3
-4
-1
-2
-3
-4
A
B
C
A1
B2
C1
A2
C2
仔细观察,你定会有所发现!
y
x
B1
将△ABC三个顶点的横坐标都减
6,纵坐标减5,又能得到什么结论?
①
②
探究
总结:图形的斜向平移,
可通过左右平移和上下平移来完成。
2
1
-1
-2
-3
-4
-6
-4
-2
2
4
x
y
1
2
3
4
-
2
1
2
-
1
-
5
-
3
-
1
-
2
0
-
3
-
4
-
4
A
C
B
A
C
B
A
C
B
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
A
1
C
1
B
1
1
2
3
一般地,图形经过两次平移后得到的图形,可以通过原来的图形作一次平移得到.
注意
(1)横变纵不变:
右移a个单位
图形上所有点(x,y)
,
(x+a,y)
图形的平移
左移a个单位
图形上所有点(x,y)
,
(x-a,y)
上移b个单位
图形上所有点(x,y)
,
(x,y+b)
下移b个单位
图形上所有点(x,y)
,
(x,y-b)
(2)纵变横不变:
图形上所有点(x,y),
(x+a,y-b)
右移a个单位,再下移b个单位
知识归纳
如图,将平行四边形ABCD向左平移2个单位长度,然后再向上平移3个单位长度,可以得到平行四边形A′B′C′D′,画出平移后的图形,并指出其各个顶点的坐标.
解:如图所示,四边形A′B′C′D′即为所求作的图形,
各点坐标分别为A′(-3,1)、B′(1,1)、C′(2,4)、
D′(-2,4).
即学即练
例
如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上一点,三角形ABC经平移后点P的对应点为P1(a+6,b+2).
(1)请画出上述平移后的三角
形A1B1C1,并写出点A、C、
A1、C1的坐标;
1
y
O
1
x
A
B
C
A1
B1
C1
解:(1)三角形A1B1C1如图所示,各点的坐标分别为A(-3,2)、C(-2,0)、A1(3,4)、C1(4,2);
P
P1
1
y
O
1
x
A
B
C
A1
B1
C1
(2)
求出以A、C、A1、C1为顶点的四边形的面积.
(2)连接AA1,CC1,
P
P1
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y)
向左平移a个单位
原图形上的点(x,y)
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y)
向下平移b个单位
原图形上的点(x,y)
(x,y+b)
(x,y-b)
图形平移与点的坐标变化间的关系
知识归纳
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
向右平移,横坐标加上一个正数
向左平移,横坐标减去一个正数
横坐标不变
向上平移,纵坐标加上一个正数
向下平移,纵坐标减去一个正数
课堂小结
1.点A`(6,3)是由点A(-2,3)经过____
______________得到的.点B(4,3)向______________得到B`(6,3)
向右平
移8个单位长度
右平移2个单位长度
检测目标
2.将点A(-3,2)向下平移3个单位,再向右平移4个单位得点B,则B点坐标是
3.将点P(0,-2)向左平移2个单位,再向上平移4个单位得点Q(x,y),则xy=
(1,-1)
-4
检测目标
4.点A’(6,3)是由点A(-2,3)向__
平移
单位长度得到的.
点B(4,3)向
平移
单位长度得到B’(6,3)
5、点A(8,9)是向__
平移
单位长度.再向
平移
单位长度得到B(6,3)
右
8个
右
2
左
2
6
下
检测目标
x
Y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
6.有相距5个单位的两点
A(-3,a),B(b,4),
AB//x轴,则a=
___
,b=
___
。
A
B
4
2或-8
检测目标
7.如图△ABC中任意一点P(x,y)经平移后对应点为P1(x+5,y+3),将△ABC作同样的平移到△A1B1C1。求A1、B1、C1的坐标
(2)
(2)
A1(3,6)
B1(1,4)
C1(7,3)
A(-2,3)
B(-4,-1)
C(2,0)
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
