人教版八年级数学下册 17.1勾股定理课时练(word版,含答案)
文档属性
| 名称 | 人教版八年级数学下册 17.1勾股定理课时练(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 694.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 00:00:00 | ||
图片预览



文档简介
17.1勾股定理
课时练
一、单选题
1.如图,在中,,AD是边BC上的中线,若,,则AD的长为(
)
A.3
B.
C.4
D.
2.如图,在△ABC中,∠C=90°,∠B=30°,CD=1,AD平分∠CAB,交CB于点D,DE垂直平分AB,垂足为E,则AE的长是(
)
A.1
B.
C.2
D.
3.下列几组数中,是勾股数的是(
)
A.1,,
B.0.3,0.4,0.5
C.15,8,17
D.,,1
4.如图,在的正方形网格中,每个小正方形的边长均为1,点,,都在格点上,若是的边上的高,则的长为(
)
A.
B.
C.
D.
5.一个直角三角形的两条边分别是9和40,则第三边的平方是( )
A.1681
B.1781
C.1519或1681
D.1519
6.如图,在中,,以点C为圆心,长为半径画弧,交于点B和点D,再分别以点B,D为圆心,大于长为半径画弧,两弧相交于点M,作射线交于点E.若,则的长度是(
)
A.3
B.
C.2
D.
7.如图,大正方形是由4个小正方形组成,小正方形的边长为2,连接小正方形的三个顶点,得到△ABC,则△ABC的边AC上的高为( )
A.
B.
C.
D.
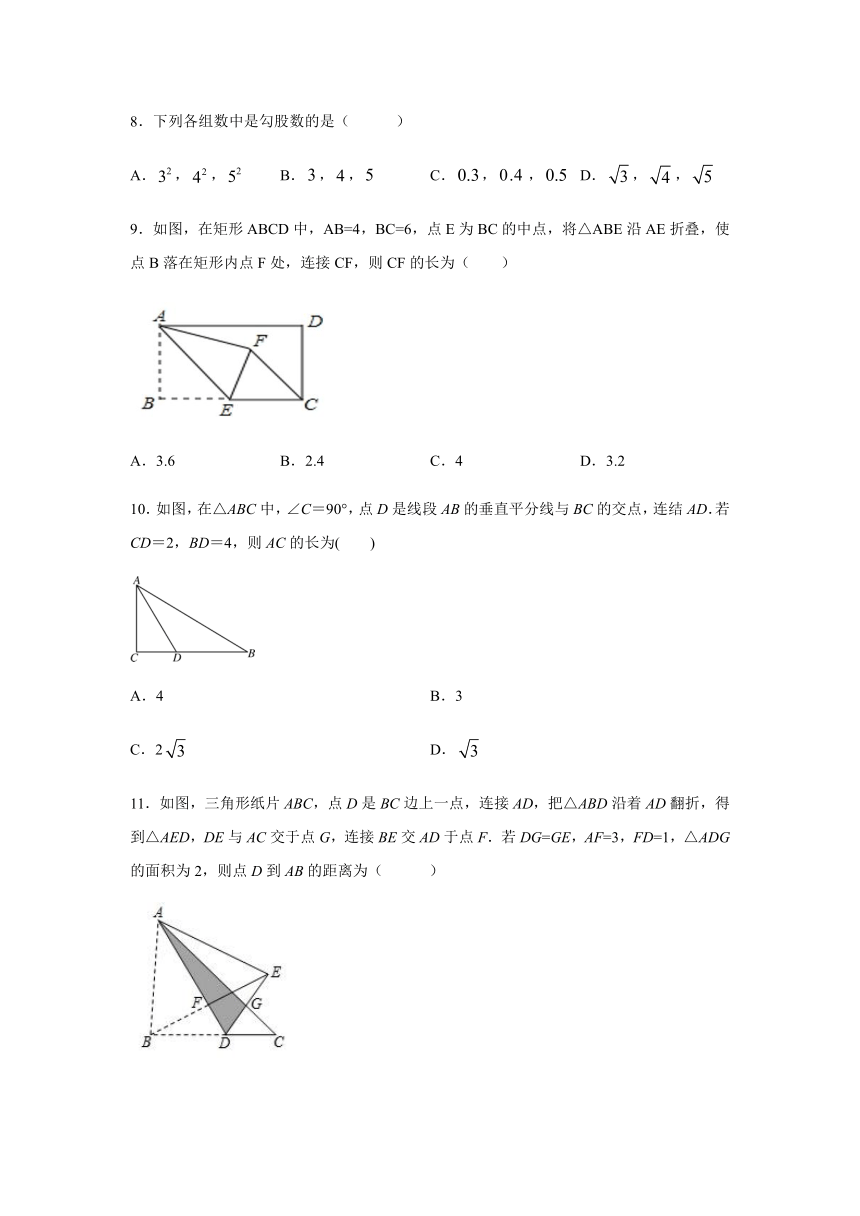
8.下列各组数中是勾股数的是( )
A.,,
B.,,
C.,,
D.,,
9.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为(
)
A.3.6
B.2.4
C.4
D.3.2
10.如图,在△ABC中,∠C=90°,点D是线段AB的垂直平分线与BC的交点,连结AD.若CD=2,BD=4,则AC的长为(
)
A.4
B.3
C.2
D.
11.如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,FD=1,△ADG的面积为2,则点D到AB的距离为( )
A.
B.
C.
D.
12.如图,在△ABC中,∠C=90°,点D在边BC上,AD=BD,DE平分∠ADB交AB于点E.若AC=12,BC=16,则AE的长为( )
A.6
B.8
C.10
D.12
13.如图,在中,,,点D,E为BC上两点.,F为外一点,且,,则下列结论:
①;②;③;④,其中正确的是
A.①②③④
B.①②④
C.①③④
D.②③
14.已知锐角△ABC的三边长恰为三个连续整数,AB>BC>CA,若边BC上的高为AD,则BD﹣DC=(
)
A.3
B.4
C.5
D.6
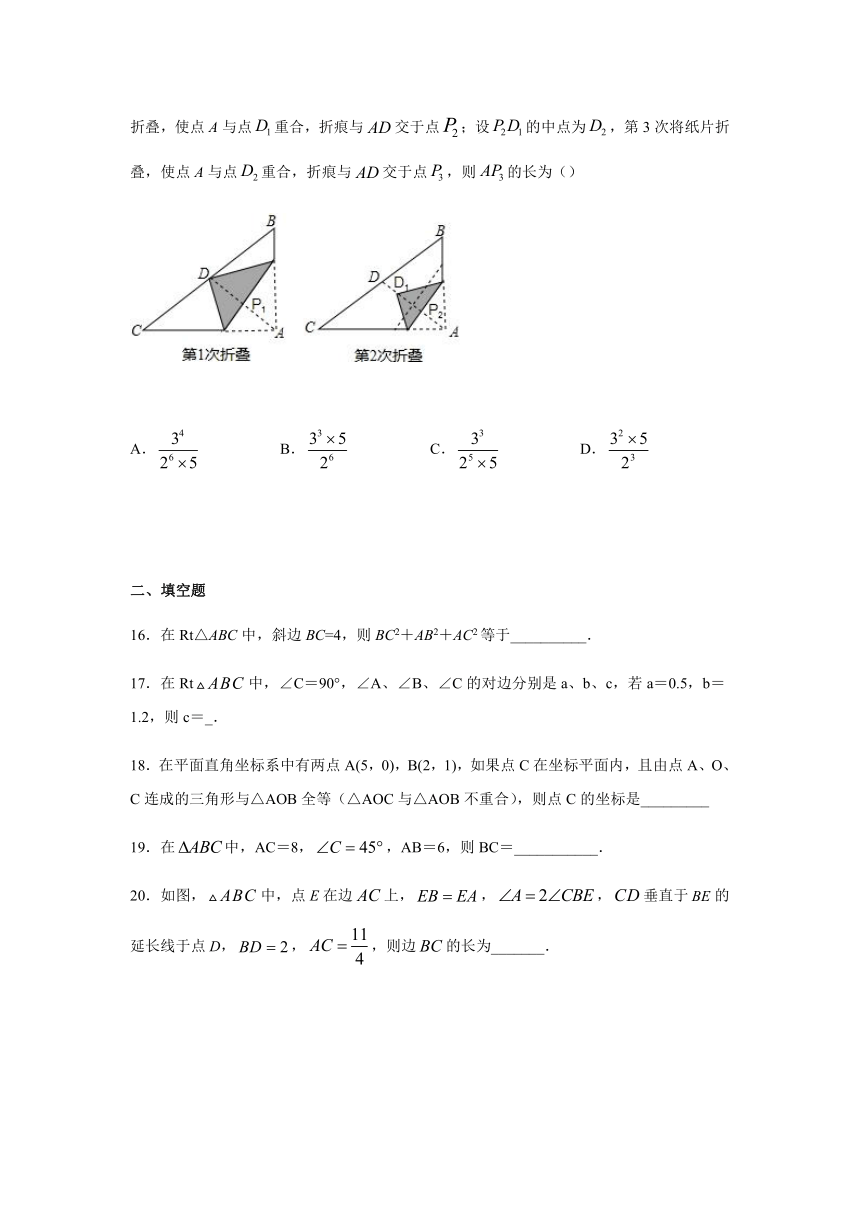
15.如图,直角三角形纸片中,,,D为斜边中点,第1次将纸片折叠,使点A与点D重合,折痕与交于点;设的中点为,第2次将纸片折叠,使点A与点重合,折痕与交于点;设的中点为,第3次将纸片折叠,使点A与点重合,折痕与交于点,则的长为()
A.
B.
C.
D.
二、填空题
16.在Rt△ABC中,斜边BC=4,则BC2+AB2+AC2等于__________.
17.在Rt中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,若a=0.5,b=1.2,则c=_.
18.在平面直角坐标系中有两点A(5,0),B(2,1),如果点C在坐标平面内,且由点A、O、C连成的三角形与△AOB全等(△AOC与△AOB不重合),则点C的坐标是_________
19.在中,AC=8,,AB=6,则BC=___________.
20.如图,中,点E在边上,,,垂直于的延长线于点D,,,则边的长为_______.
三、解答题
21.如图1,在中,,,是的高,且.
(1)求的长;
(2)是边上的一点,作射线,分别过点,作于点,于点,如图2,若,求与的和.
22.如果正方形网格中的每一个小正方形边长都是1则每个小格的顶点叫做格点.
(1)在图1中,以格点为顶点画一个三角形,使三角形的三边长分别为,3,,;
(2)在图2中,线段的端点在格点上,请画出以为一边的三角形使这个三角形的面积为6(要求至少画出3个);
(3)在图3中,的顶点M,N在格点上,P在小正方形的边上,问这个三角形的面积相当于多少个小方格的面积?
23.和都是等腰直角三角形,.
(1)如图1,点,在,上,则,满足怎样的数量关系和位置关系?(直接写出答案)
(2)如图2,点在内部,点在外部.连结,,则,满足怎样的数量关系和位置关系?请说明理由;
(3)如图3,点,都在外部,连结,,,,与相交于点.
①若,求四边形的面积;
②若,,设,,求与之间的函数关系式.
24.如图,在中,,,交于点D.动点P从点C出发,按的路径运动,且速度为,设出发时间为.
(1)求的面积及的长;
(2)当时,求证:;
(3)当点P在边上运动时,若是等腰三角形,求出所有满足条件的t的值.
参考答案
1--10BBCDC
AABAC
11--15BCABD
16.32
17.1.3
18.或或
19.
20.
21.(1)3;(2).
22.1)如图所示,
(2)如图所示:
(3)△MNP的面积为:=10,
故这个小三角形的面积相当于10个小正方形的面积.
23.(1)∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,
∴AB-AD=AC-AE,即:BD=CE,
∵BD、CE相交于点A,∠BAC=90°,
∴BD⊥CE;
(2)∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC-∠DAC,
∠CAE=∠DAE-∠DAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE,
∴BD=CE,
延长BD,分别交AC,CE于F,G,BD=CE,
∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠AFB=∠GFC,
∴∠CGF=∠BAF=90°,即BD⊥CE;
(3)①∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC+∠DAC,∠CAE=∠DAE+∠DAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE,
∴BD=CE=,∠ABD=∠ACE
∵∠1=∠2
∴∠BHC=∠BAC=90°
∴S四边形BCDE=S△BCE+S△DCE==
=,
②∵∠BHC=90°,
∴CD2+EB2=CH2+HD2+EH2+HB2=CH2+HB2+EH2+HD2=BC2+DE2=2AB2+2AD2=26,即:x+y=26,
∴y=26-x.
24.(1)如图,作AH⊥BC于H.
∵AB=AC,
∴BH=CH=BC=3,
∴AH==4,
∴S△ABC==12,
∵S△ABC=,
∴BD==;
(2)如图,当t=3.2时,3.2×2=6.4,
此时点P在AB边上,AP=6.4-5=1.4,
由(1)可知AD===1.4,
∴AP=AD,
∵AC=AB,∠A=∠A,
∴△APC≌△ADB(SAS),
∴∠APC=∠ADB=90°,
∴PC⊥AB.
(3)∵BD=4.8,CD=AC-AD=3.6,BD≠CD,
∴BD≠DP,
当点P在BC上时,CP=16-2t,BP=2t-10,
当PD=BP时,
∠PBD=∠PDB,
∵∠BDC=90°,
∴∠PBD+∠C=90°,∠PDB+∠PDC=90°,
∴∠C=∠PDC,
∴PD=PC,
则2t-10=16-2t,
解得:t=6.5;
当BD=BP时,
BP=4.8,
则t=(4.8+5+5)÷2=7.4,
综上:当△BDP为等腰三角形时,t的值为6.5或7.4.
试卷第1页,总3页
课时练
一、单选题
1.如图,在中,,AD是边BC上的中线,若,,则AD的长为(
)
A.3
B.
C.4
D.
2.如图,在△ABC中,∠C=90°,∠B=30°,CD=1,AD平分∠CAB,交CB于点D,DE垂直平分AB,垂足为E,则AE的长是(
)
A.1
B.
C.2
D.
3.下列几组数中,是勾股数的是(
)
A.1,,
B.0.3,0.4,0.5
C.15,8,17
D.,,1
4.如图,在的正方形网格中,每个小正方形的边长均为1,点,,都在格点上,若是的边上的高,则的长为(
)
A.
B.
C.
D.
5.一个直角三角形的两条边分别是9和40,则第三边的平方是( )
A.1681
B.1781
C.1519或1681
D.1519
6.如图,在中,,以点C为圆心,长为半径画弧,交于点B和点D,再分别以点B,D为圆心,大于长为半径画弧,两弧相交于点M,作射线交于点E.若,则的长度是(
)
A.3
B.
C.2
D.
7.如图,大正方形是由4个小正方形组成,小正方形的边长为2,连接小正方形的三个顶点,得到△ABC,则△ABC的边AC上的高为( )
A.
B.
C.
D.
8.下列各组数中是勾股数的是( )
A.,,
B.,,
C.,,
D.,,
9.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为(
)
A.3.6
B.2.4
C.4
D.3.2
10.如图,在△ABC中,∠C=90°,点D是线段AB的垂直平分线与BC的交点,连结AD.若CD=2,BD=4,则AC的长为(
)
A.4
B.3
C.2
D.
11.如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,FD=1,△ADG的面积为2,则点D到AB的距离为( )
A.
B.
C.
D.
12.如图,在△ABC中,∠C=90°,点D在边BC上,AD=BD,DE平分∠ADB交AB于点E.若AC=12,BC=16,则AE的长为( )
A.6
B.8
C.10
D.12
13.如图,在中,,,点D,E为BC上两点.,F为外一点,且,,则下列结论:
①;②;③;④,其中正确的是
A.①②③④
B.①②④
C.①③④
D.②③
14.已知锐角△ABC的三边长恰为三个连续整数,AB>BC>CA,若边BC上的高为AD,则BD﹣DC=(
)
A.3
B.4
C.5
D.6
15.如图,直角三角形纸片中,,,D为斜边中点,第1次将纸片折叠,使点A与点D重合,折痕与交于点;设的中点为,第2次将纸片折叠,使点A与点重合,折痕与交于点;设的中点为,第3次将纸片折叠,使点A与点重合,折痕与交于点,则的长为()
A.
B.
C.
D.
二、填空题
16.在Rt△ABC中,斜边BC=4,则BC2+AB2+AC2等于__________.
17.在Rt中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,若a=0.5,b=1.2,则c=_.
18.在平面直角坐标系中有两点A(5,0),B(2,1),如果点C在坐标平面内,且由点A、O、C连成的三角形与△AOB全等(△AOC与△AOB不重合),则点C的坐标是_________
19.在中,AC=8,,AB=6,则BC=___________.
20.如图,中,点E在边上,,,垂直于的延长线于点D,,,则边的长为_______.
三、解答题
21.如图1,在中,,,是的高,且.
(1)求的长;
(2)是边上的一点,作射线,分别过点,作于点,于点,如图2,若,求与的和.
22.如果正方形网格中的每一个小正方形边长都是1则每个小格的顶点叫做格点.
(1)在图1中,以格点为顶点画一个三角形,使三角形的三边长分别为,3,,;
(2)在图2中,线段的端点在格点上,请画出以为一边的三角形使这个三角形的面积为6(要求至少画出3个);
(3)在图3中,的顶点M,N在格点上,P在小正方形的边上,问这个三角形的面积相当于多少个小方格的面积?
23.和都是等腰直角三角形,.
(1)如图1,点,在,上,则,满足怎样的数量关系和位置关系?(直接写出答案)
(2)如图2,点在内部,点在外部.连结,,则,满足怎样的数量关系和位置关系?请说明理由;
(3)如图3,点,都在外部,连结,,,,与相交于点.
①若,求四边形的面积;
②若,,设,,求与之间的函数关系式.
24.如图,在中,,,交于点D.动点P从点C出发,按的路径运动,且速度为,设出发时间为.
(1)求的面积及的长;
(2)当时,求证:;
(3)当点P在边上运动时,若是等腰三角形,求出所有满足条件的t的值.
参考答案
1--10BBCDC
AABAC
11--15BCABD
16.32
17.1.3
18.或或
19.
20.
21.(1)3;(2).
22.1)如图所示,
(2)如图所示:
(3)△MNP的面积为:=10,
故这个小三角形的面积相当于10个小正方形的面积.
23.(1)∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,
∴AB-AD=AC-AE,即:BD=CE,
∵BD、CE相交于点A,∠BAC=90°,
∴BD⊥CE;
(2)∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC-∠DAC,
∠CAE=∠DAE-∠DAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE,
∴BD=CE,
延长BD,分别交AC,CE于F,G,BD=CE,
∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠AFB=∠GFC,
∴∠CGF=∠BAF=90°,即BD⊥CE;
(3)①∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC+∠DAC,∠CAE=∠DAE+∠DAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE,
∴BD=CE=,∠ABD=∠ACE
∵∠1=∠2
∴∠BHC=∠BAC=90°
∴S四边形BCDE=S△BCE+S△DCE==
=,
②∵∠BHC=90°,
∴CD2+EB2=CH2+HD2+EH2+HB2=CH2+HB2+EH2+HD2=BC2+DE2=2AB2+2AD2=26,即:x+y=26,
∴y=26-x.
24.(1)如图,作AH⊥BC于H.
∵AB=AC,
∴BH=CH=BC=3,
∴AH==4,
∴S△ABC==12,
∵S△ABC=,
∴BD==;
(2)如图,当t=3.2时,3.2×2=6.4,
此时点P在AB边上,AP=6.4-5=1.4,
由(1)可知AD===1.4,
∴AP=AD,
∵AC=AB,∠A=∠A,
∴△APC≌△ADB(SAS),
∴∠APC=∠ADB=90°,
∴PC⊥AB.
(3)∵BD=4.8,CD=AC-AD=3.6,BD≠CD,
∴BD≠DP,
当点P在BC上时,CP=16-2t,BP=2t-10,
当PD=BP时,
∠PBD=∠PDB,
∵∠BDC=90°,
∴∠PBD+∠C=90°,∠PDB+∠PDC=90°,
∴∠C=∠PDC,
∴PD=PC,
则2t-10=16-2t,
解得:t=6.5;
当BD=BP时,
BP=4.8,
则t=(4.8+5+5)÷2=7.4,
综上:当△BDP为等腰三角形时,t的值为6.5或7.4.
试卷第1页,总3页
