4 二元一次方程与一次函数 课件(共15张PPT)
文档属性
| 名称 | 4 二元一次方程与一次函数 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 19:36:41 | ||
图片预览






文档简介
第七章 二元一次方程组
4 二元一次方程与一次函数
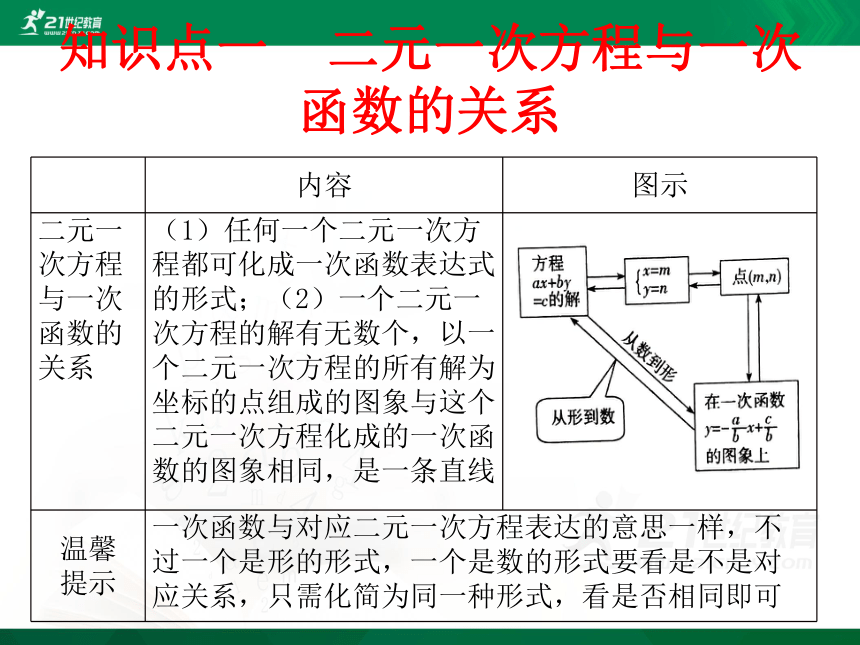
知识点一 二元一次方程与一次函数的关系
内容
图示
二元一次方程与一次函数的关系
(1)任何一个二元一次方程都可化成一次函数表达式的形式;(2)一个二元一次方程的解有无数个,以一个二元一次方程的所有解为坐标的点组成的图象与这个二元一次方程化成的一次函数的图象相同,是一条直线
温馨
提示
一次函数与对应二元一次方程表达的意思一样,不过一个是形的形式,一个是数的形式要看是不是对应关系,只需化简为同一种形式,看是否相同即可
例1 以方程
的解为坐标的所有点都在
函数y=____________的图象上.
解析
因为以方程
的解为坐标的所有点组成的图象就是该方程对应一次函数的图象,所以这个一次函数的表达式就是
的变形,即用含x的代数式表示y,由此可得 .
答案
知识点二 二元一次方程组与一次函数的关系
二元一次方程组与一次函数的关系
两个一次函数y=k1x+b1(k1≠0),y=k2x+b2(k2≠0)的图象的交点坐标就是关于x、y的方程组 (k1≠0,k2≠0)的解.反之,方程组 (k1≠0,k2≠0)的解就是一次函数y=k1x+b1(k1≠0),y=k2x+b2(k2≠0)的图象的交点坐标
温馨提示
两条直线y=k1x+b1(k1≠0)、y=k2x+b2(k2≠0):
(1)若k1=k2,b1≠b2,则它们平行,无交点,方程组 无解;(2)若k1=k2,b1=b2,则它们重合,有无数个交点,方程组 有无穷多个解;
(3)若k1≠k2,则它们相交,只有一个交点,方程组 有唯一解
例2 如图所示,在平面直角坐标系中,一次函数y=kx+b和y=mx+n的图象相交于点(2,-1),则关于x、y的方程组
的解是( )
A. B. C. D.
解析 两函数图象的交点坐标为两函数解析式组成的方程组的解,从题图上看,两直线交点的坐标为(2,-1),因此方程组
的解是 .
故选B.
答案 B
点拨:
二元一次方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这对未知数的值也同时满足两个相应的一次函数关系式,因此二元一次方程组的解就是两个相应的一次函数图象的交点坐标.
知识点三 待定系数法
温馨提示
待定系数法的步骤可总结为“设、代、解、写”
例3 某商场经营一批进价为2元一件的小商品,在市场营销中发现此商品的日销售单价x元与日销售量y件之间有如下表所示的关系,试确定日销售量y(件)与日销售单价x(元)之间的函数关系式.
x
3
5
8
10
11
y
18
14
8
4
2
解析
由题中的表格知,y是x的一次函数,可设y与x的函数关系式为y=kx+b(k≠0),
由题意,得
解得 .
∴y与x之间的函数关系式为y=-2x+24,且(8,8),(10,4),(11,2)这三个点均满足y=-2x+24.
故日销售量y(件)与日销售单价x(元)之间的函数关系式为y=-2x+24.
经典例题
题型 一次函数表达式的确定及综合应用
例 如图所示,已知点A(6,0)、点B(0,2).
(1)求直线AB所对应的函数表达式;
(2)若C为直线AB上一动点,当△OBC的面积为3时,试求点C的坐标.
解析 (1)设直线AB所对应的函数表达式为y=kx+b(k≠0),
根据题意,得
,解得
∴直线AB所对应的函数表达式为
(2)∵B(0,2),∴OB=2.又∵△OBC的面积为3,
∴△OBC中OB边上的高为3,∴点C的横坐标为-3或3.
当x=-3时,
=3;当x=3时,
=1,
∴点C的坐标为(-3,3)或(3,1).
点拨:
确定一次函数y=kx+b的表达式,只要确定k和b的值即可.一般需要函数y=kx+b的图象上的两个点的坐标,把两个点的坐标分别代入y=kx+b中,列出关于k,b的二元一次方程组,就可使问题得到解决.
4 二元一次方程与一次函数
知识点一 二元一次方程与一次函数的关系
内容
图示
二元一次方程与一次函数的关系
(1)任何一个二元一次方程都可化成一次函数表达式的形式;(2)一个二元一次方程的解有无数个,以一个二元一次方程的所有解为坐标的点组成的图象与这个二元一次方程化成的一次函数的图象相同,是一条直线
温馨
提示
一次函数与对应二元一次方程表达的意思一样,不过一个是形的形式,一个是数的形式要看是不是对应关系,只需化简为同一种形式,看是否相同即可
例1 以方程
的解为坐标的所有点都在
函数y=____________的图象上.
解析
因为以方程
的解为坐标的所有点组成的图象就是该方程对应一次函数的图象,所以这个一次函数的表达式就是
的变形,即用含x的代数式表示y,由此可得 .
答案
知识点二 二元一次方程组与一次函数的关系
二元一次方程组与一次函数的关系
两个一次函数y=k1x+b1(k1≠0),y=k2x+b2(k2≠0)的图象的交点坐标就是关于x、y的方程组 (k1≠0,k2≠0)的解.反之,方程组 (k1≠0,k2≠0)的解就是一次函数y=k1x+b1(k1≠0),y=k2x+b2(k2≠0)的图象的交点坐标
温馨提示
两条直线y=k1x+b1(k1≠0)、y=k2x+b2(k2≠0):
(1)若k1=k2,b1≠b2,则它们平行,无交点,方程组 无解;(2)若k1=k2,b1=b2,则它们重合,有无数个交点,方程组 有无穷多个解;
(3)若k1≠k2,则它们相交,只有一个交点,方程组 有唯一解
例2 如图所示,在平面直角坐标系中,一次函数y=kx+b和y=mx+n的图象相交于点(2,-1),则关于x、y的方程组
的解是( )
A. B. C. D.
解析 两函数图象的交点坐标为两函数解析式组成的方程组的解,从题图上看,两直线交点的坐标为(2,-1),因此方程组
的解是 .
故选B.
答案 B
点拨:
二元一次方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这对未知数的值也同时满足两个相应的一次函数关系式,因此二元一次方程组的解就是两个相应的一次函数图象的交点坐标.
知识点三 待定系数法
温馨提示
待定系数法的步骤可总结为“设、代、解、写”
例3 某商场经营一批进价为2元一件的小商品,在市场营销中发现此商品的日销售单价x元与日销售量y件之间有如下表所示的关系,试确定日销售量y(件)与日销售单价x(元)之间的函数关系式.
x
3
5
8
10
11
y
18
14
8
4
2
解析
由题中的表格知,y是x的一次函数,可设y与x的函数关系式为y=kx+b(k≠0),
由题意,得
解得 .
∴y与x之间的函数关系式为y=-2x+24,且(8,8),(10,4),(11,2)这三个点均满足y=-2x+24.
故日销售量y(件)与日销售单价x(元)之间的函数关系式为y=-2x+24.
经典例题
题型 一次函数表达式的确定及综合应用
例 如图所示,已知点A(6,0)、点B(0,2).
(1)求直线AB所对应的函数表达式;
(2)若C为直线AB上一动点,当△OBC的面积为3时,试求点C的坐标.
解析 (1)设直线AB所对应的函数表达式为y=kx+b(k≠0),
根据题意,得
,解得
∴直线AB所对应的函数表达式为
(2)∵B(0,2),∴OB=2.又∵△OBC的面积为3,
∴△OBC中OB边上的高为3,∴点C的横坐标为-3或3.
当x=-3时,
=3;当x=3时,
=1,
∴点C的坐标为(-3,3)或(3,1).
点拨:
确定一次函数y=kx+b的表达式,只要确定k和b的值即可.一般需要函数y=kx+b的图象上的两个点的坐标,把两个点的坐标分别代入y=kx+b中,列出关于k,b的二元一次方程组,就可使问题得到解决.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
