二次函数与一元二次方程
图片预览

文档简介
(共12张PPT)
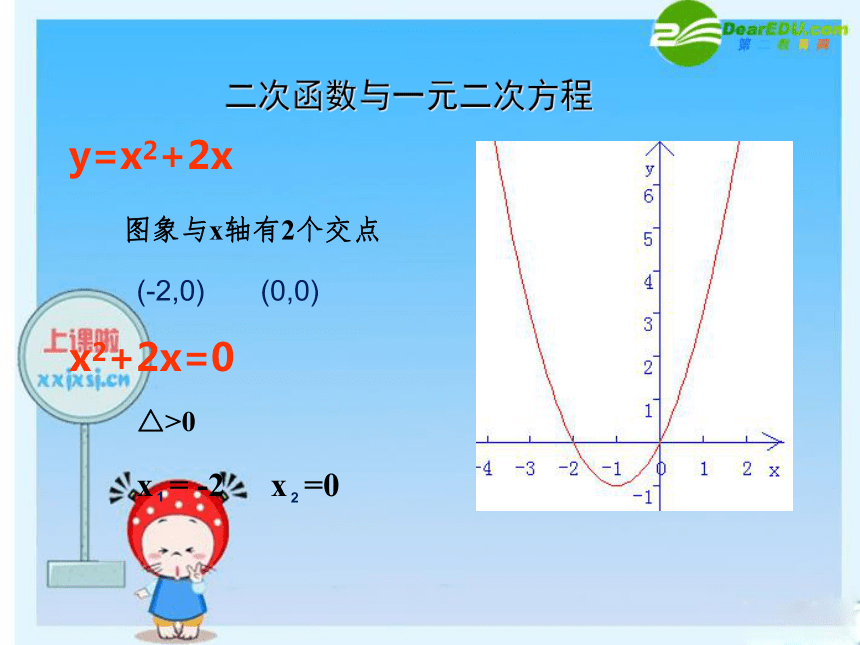
y=x2+2x
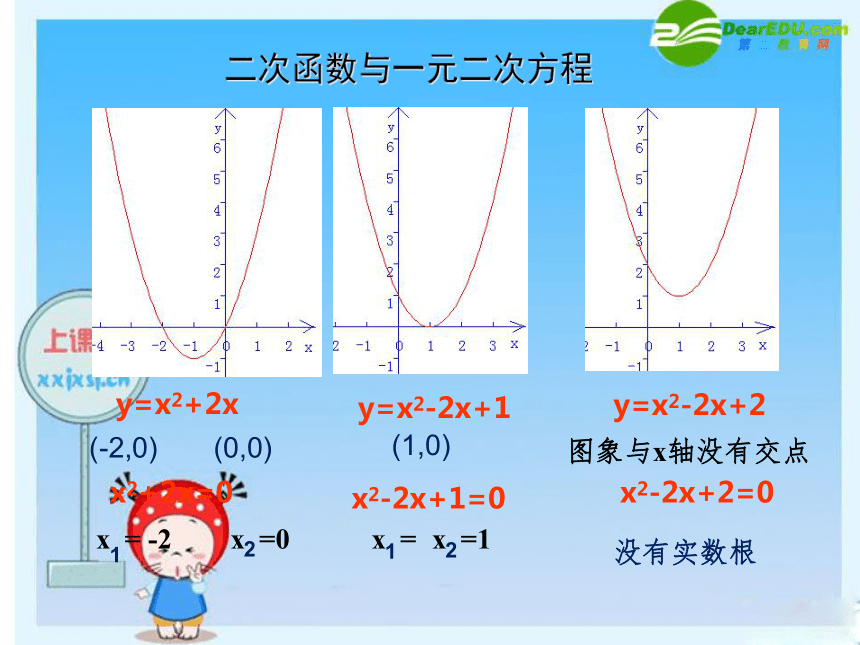
y=x2+2x
图象与x轴有2个交点
(-2,0) (0,0)
x2+2x=0
△>0
x = -2
x =0
1
2
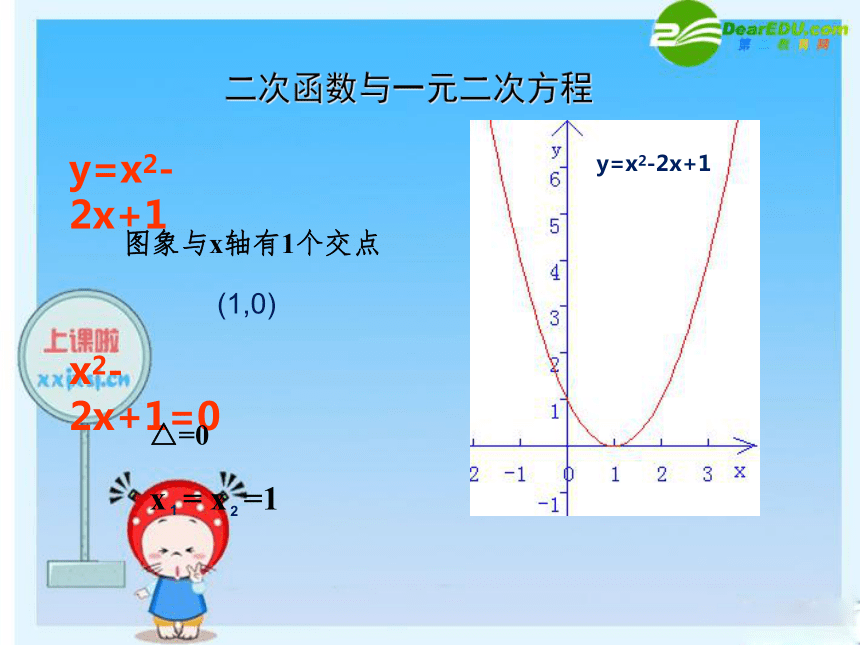
二次函数与一元二次方程
y=x2-2x+1
图象与x轴有1个交点
(1,0)
x2-2x+1=0
△=0
x =
1
x =1
2
y=x2-2x+1
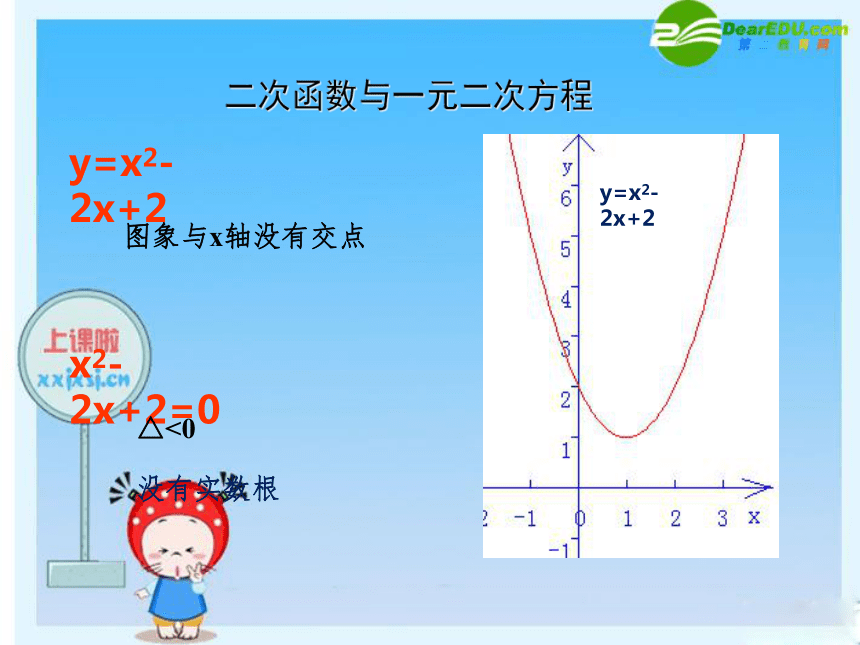
二次函数与一元二次方程
y=x2-2x+2
图象与x轴没有交点
x2-2x+2=0
△<0
y=x2-2x+2
没有实数根
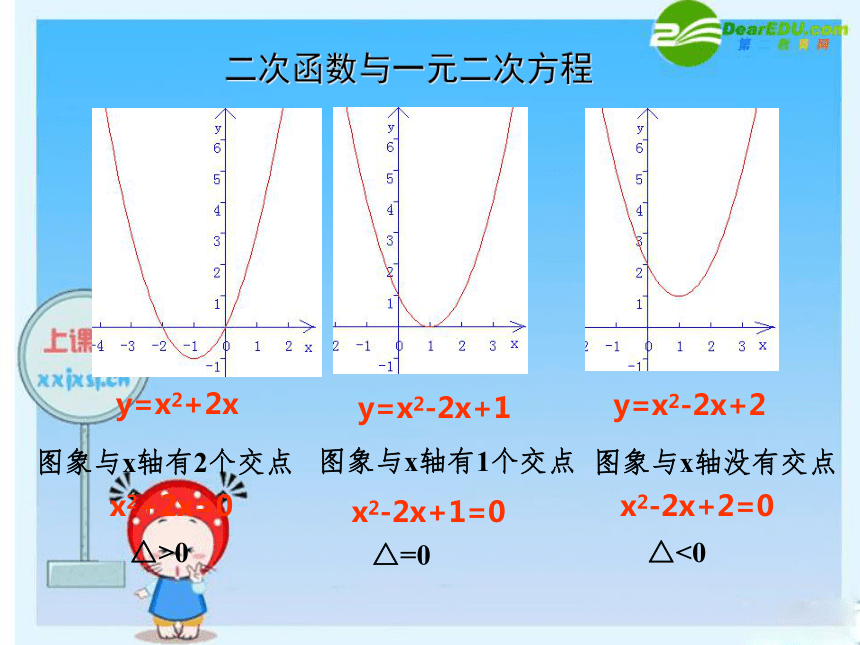
二次函数与一元二次方程
二次函数与一元二次方程
y=x2+2x
图象与x轴有2个交点
x2+2x=0
△>0
y=x2-2x+1
图象与x轴有1个交点
x2-2x+1=0
△=0
y=x2-2x+2
图象与x轴没有交点
x2-2x+2=0
△<0
y=x2+2x
x2+2x=0
y=x2-2x+1
x2-2x+1=0
y=x2-2x+2
x2-2x+2=0
(-2,0) (0,0)
x = -2
x =0
1
2
(1,0)
x =
1
x =1
2
图象与x轴没有交点
没有实数根
二次函数与一元二次方程
二次函数与一元二次方程
y=x2+2x
图象与x轴有2个交点
x2+2x=0
△>0
y=x2-2x+1
图象与x轴有1个交点
x2-2x+1=0
△=0
y=x2-2x+2
图象与x轴没有交点
x2-2x+2=0
△<0
y=x2+2x
x2+2x=0
y=x2-2x+1
x2-2x+1=0
y=x2-2x+2
x2-2x+2=0
(-2,0) (0,0)
x = -2
x =0
1
2
(1,0)
x =
1
x =1
2
图象与x轴没有交点
没有实数根
二次函数与一元二次方程
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
二次函数与一元二次方程
当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
抛物线y=ax2+bx+c
抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明:
1、△>0 一元二次方程ax2+bx+c=0有两个不等的实数根
与x轴有两个交点
抛物线y=ax2+bx+c
2、△=0 一元二次方程ax2+bx+c=0
与x轴有唯一公共点
抛物线y=ax2+bx+c
3、△<0 一元二次方程ax2+bx+c=0
与x轴没有公共点
没有实数根
有两个相等的实数根
解:∵A、B在轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
∴A(1,0) , B(2,0)
抛物线y=ax2+bx+c(a≠0)的图象全部在轴下方的条件是( )
(A)a<0 b2-4ac≤0(B)a<0 b2-4ac>0
(C)a>0 b2-4ac>0 (D)a<0 b2-4ac<0
D
已知二次函数y=-ax2,下列说法不正确的是( )
A.当a>0,x≠0时,y总取负值
B.当a<0,x<0时,y随x的增大而减小
C.当a<0时,函数图象有最低点,即y有最小值
D.当x<0,y= -ax2的对称轴是y轴
D
y=x2+2x
y=x2+2x
图象与x轴有2个交点
(-2,0) (0,0)
x2+2x=0
△>0
x = -2
x =0
1
2
二次函数与一元二次方程
y=x2-2x+1
图象与x轴有1个交点
(1,0)
x2-2x+1=0
△=0
x =
1
x =1
2
y=x2-2x+1
二次函数与一元二次方程
y=x2-2x+2
图象与x轴没有交点
x2-2x+2=0
△<0
y=x2-2x+2
没有实数根
二次函数与一元二次方程
二次函数与一元二次方程
y=x2+2x
图象与x轴有2个交点
x2+2x=0
△>0
y=x2-2x+1
图象与x轴有1个交点
x2-2x+1=0
△=0
y=x2-2x+2
图象与x轴没有交点
x2-2x+2=0
△<0
y=x2+2x
x2+2x=0
y=x2-2x+1
x2-2x+1=0
y=x2-2x+2
x2-2x+2=0
(-2,0) (0,0)
x = -2
x =0
1
2
(1,0)
x =
1
x =1
2
图象与x轴没有交点
没有实数根
二次函数与一元二次方程
二次函数与一元二次方程
y=x2+2x
图象与x轴有2个交点
x2+2x=0
△>0
y=x2-2x+1
图象与x轴有1个交点
x2-2x+1=0
△=0
y=x2-2x+2
图象与x轴没有交点
x2-2x+2=0
△<0
y=x2+2x
x2+2x=0
y=x2-2x+1
x2-2x+1=0
y=x2-2x+2
x2-2x+2=0
(-2,0) (0,0)
x = -2
x =0
1
2
(1,0)
x =
1
x =1
2
图象与x轴没有交点
没有实数根
二次函数与一元二次方程
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
二次函数与一元二次方程
当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
抛物线y=ax2+bx+c
抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明:
1、△>0 一元二次方程ax2+bx+c=0有两个不等的实数根
与x轴有两个交点
抛物线y=ax2+bx+c
2、△=0 一元二次方程ax2+bx+c=0
与x轴有唯一公共点
抛物线y=ax2+bx+c
3、△<0 一元二次方程ax2+bx+c=0
与x轴没有公共点
没有实数根
有两个相等的实数根
解:∵A、B在轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
∴A(1,0) , B(2,0)
抛物线y=ax2+bx+c(a≠0)的图象全部在轴下方的条件是( )
(A)a<0 b2-4ac≤0(B)a<0 b2-4ac>0
(C)a>0 b2-4ac>0 (D)a<0 b2-4ac<0
D
已知二次函数y=-ax2,下列说法不正确的是( )
A.当a>0,x≠0时,y总取负值
B.当a<0,x<0时,y随x的增大而减小
C.当a<0时,函数图象有最低点,即y有最小值
D.当x<0,y= -ax2的对称轴是y轴
D
