九年级数学解直角三角形(仰角与俯角)课件北师大版
文档属性
| 名称 | 九年级数学解直角三角形(仰角与俯角)课件北师大版 |

|
|
| 格式 | rar | ||
| 文件大小 | 535.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-12 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
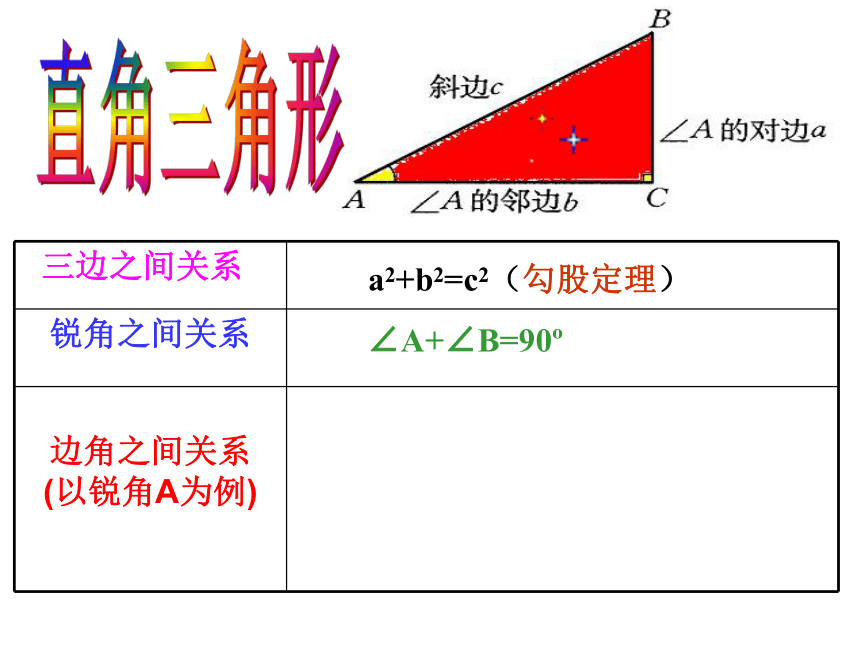
直角三角形的边角关系
仰角与俯角
学习永远是件快乐而有趣的事!
多彩的数学世界及其解决实际问题的魅力将把你引入一个奇妙的境界!
三边之间关系
锐角之间关系
边角之间关系
(以锐角A为例)
a2+b2=c2(勾股定理)
∠A+∠B=90
想一想
A
B
C
a
b
c
sinA=
a
c
cosA=
c
b
tanA=
a
b
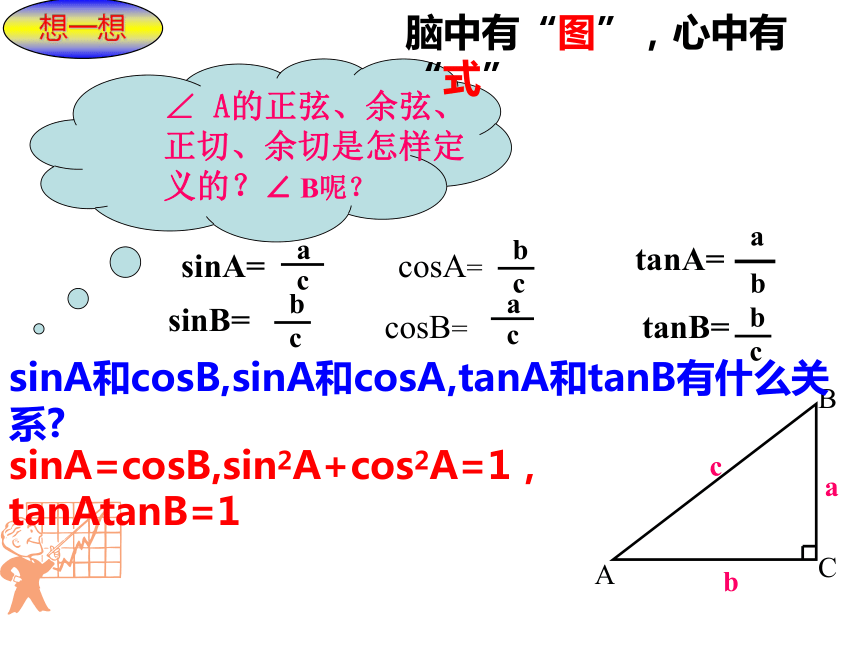
∠ A的正弦、余弦、正切、余切是怎样定义的?∠ B呢?
sinB=
cosB=
c
b
a
c
sinA和cosB,sinA和cosA,tanA和tanB有什么关系
脑中有“图”,心中有“式”
sinA=cosB,sin2A+cos2A=1,tanAtanB=1
tanB=
c
b
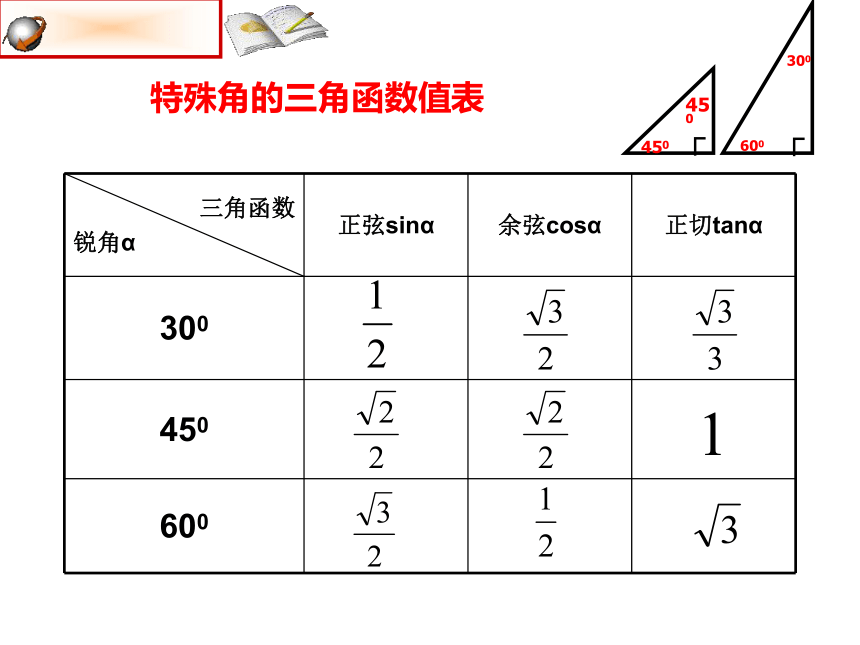
特殊角的三角函数值表
三角函数
锐角α 正弦sinα 余弦cosα 正切tanα
300
450
600
┌
┌
300
600
450
450
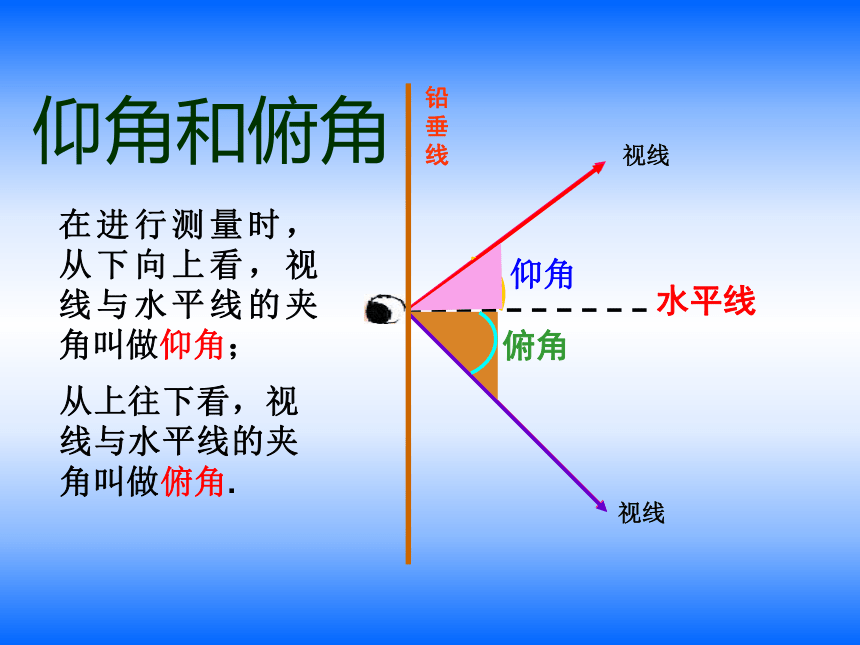
仰角和俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
水平线
视线
视线
铅垂线
仰角
俯角
从上往下看,视线与水平线的夹角叫做俯角.
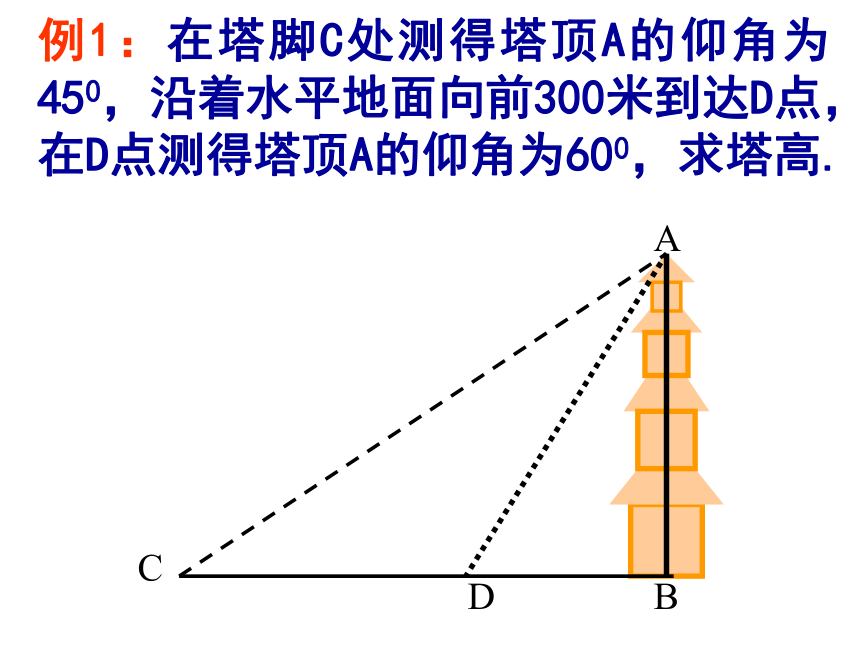
例1:在塔脚C处测得塔顶A的仰角为450,沿着水平地面向前300米到达D点,在D点测得塔顶A的仰角为600,求塔高.
A
B
C
D
A
B
D
C
解:设 AB = x m
在Rt△ACB中
∵tan45 = ∴BC=
tan45
x
x
Rt△ADB中 ∵ tan60 =
∴BD=
AB
BC
x
tan60
∵ BC -BD = CD
AB
BD
45
60
300
tan45
x
tan60
1
1
300
∴x=
150(3+ )m
解: 在Rt△ADB中,
AB= BDtan∠ADB=BDtan60°.
在Rt△ACB中,
AB= BCtan ∠ACB=BCtan45°.
∴ BDtan60°=BCtan45°
即 BDtan60°=(BD+300)tan45°,
C
D
B
A
﹚
﹚
60°
45°
300m
∴ BD=150( +1)米
∴ AB=BDtan60°=150(3+ )米
例2:在山顶处有一铁塔AB,在塔顶的A处测得地面上一点C的俯角 为60°,在塔底B测得点C的俯角为 =45°,已知塔高AB=30米,
(1)在原图上画出点A望点C的俯角和点B望点C的俯角,并分别标出两俯角的大小。
(2)求出山高BD。
B
A
D
C
做一做
如图,某市为庆祝“两会”召开,在甲建筑物上的A点到E点挂一长20米的宣传条幅,某人在乙建筑物顶部D点测得条幅顶端A点的仰角为 45°,测得此条幅底端E点的俯角为30°,求BC的长
A
E
D
C
B
如图:大楼高30米,远处有一灯塔BC,小明在楼底A处测的塔顶的仰角为45度,爬到楼顶D测的塔顶的仰角30度,求塔高BC及大楼与灯塔之间的距离
A
D
B
E
C
达标检测
A
B
C
在山脚C处测得山顶A的仰角为450。问题如下:
沿着坡角为30 °的斜坡前进300米到达D点,在D点测得山顶A的仰角为600 ,求山高AB。
30°
D
E
F
x
x
动 手 做 一 做
1、一架飞机以300角俯冲400米,
则飞机的高度变化情况是( )
A.升高400米
B.下降400米
C.下降200米
D.下降 米
2、在山顶上D处有一铁塔,在塔顶B处测得 地面上一点A的俯角α=60o,在塔底D测得点A的俯角β=45o,已知塔高BD=30米,
则山高 CD=__________米.
A
B
C
D
α
β
C
本节课你有什么收获
1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。
2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
已知斜边求直边,
已知直边求直边,
已知两边求一边,
已知两边求一角,
已知锐角求锐角,
已知直边求斜边,
计算方法要选择,
正弦余弦很方便;
正切余切理当然;
函数关系要选好;
勾股定理最方便;
互余关系要记好;
用除还需正余弦;
能用乘法不用除.
优选关系式
求山高或建筑物的高;测量河的宽度或物体的长度;航行航海问题等.解决这类问题的关键是先画出测量示意图,把实际问题转化为数学问题,利用直角三角形中角、边之间的数量关系求出所要求的距离或角度.
应用解直角三角形知识解应用题时,可按以下思维过程进行:
(1)画出测量示意图;
(2)寻找直角三角形,若找不到,可构造;
(3) 解直角三角形,若不可直接求解,利用题中的数 量关系,设x求解.
方法归纳
直角三角形的边角关系
仰角与俯角
学习永远是件快乐而有趣的事!
多彩的数学世界及其解决实际问题的魅力将把你引入一个奇妙的境界!
三边之间关系
锐角之间关系
边角之间关系
(以锐角A为例)
a2+b2=c2(勾股定理)
∠A+∠B=90
想一想
A
B
C
a
b
c
sinA=
a
c
cosA=
c
b
tanA=
a
b
∠ A的正弦、余弦、正切、余切是怎样定义的?∠ B呢?
sinB=
cosB=
c
b
a
c
sinA和cosB,sinA和cosA,tanA和tanB有什么关系
脑中有“图”,心中有“式”
sinA=cosB,sin2A+cos2A=1,tanAtanB=1
tanB=
c
b
特殊角的三角函数值表
三角函数
锐角α 正弦sinα 余弦cosα 正切tanα
300
450
600
┌
┌
300
600
450
450
仰角和俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
水平线
视线
视线
铅垂线
仰角
俯角
从上往下看,视线与水平线的夹角叫做俯角.
例1:在塔脚C处测得塔顶A的仰角为450,沿着水平地面向前300米到达D点,在D点测得塔顶A的仰角为600,求塔高.
A
B
C
D
A
B
D
C
解:设 AB = x m
在Rt△ACB中
∵tan45 = ∴BC=
tan45
x
x
Rt△ADB中 ∵ tan60 =
∴BD=
AB
BC
x
tan60
∵ BC -BD = CD
AB
BD
45
60
300
tan45
x
tan60
1
1
300
∴x=
150(3+ )m
解: 在Rt△ADB中,
AB= BDtan∠ADB=BDtan60°.
在Rt△ACB中,
AB= BCtan ∠ACB=BCtan45°.
∴ BDtan60°=BCtan45°
即 BDtan60°=(BD+300)tan45°,
C
D
B
A
﹚
﹚
60°
45°
300m
∴ BD=150( +1)米
∴ AB=BDtan60°=150(3+ )米
例2:在山顶处有一铁塔AB,在塔顶的A处测得地面上一点C的俯角 为60°,在塔底B测得点C的俯角为 =45°,已知塔高AB=30米,
(1)在原图上画出点A望点C的俯角和点B望点C的俯角,并分别标出两俯角的大小。
(2)求出山高BD。
B
A
D
C
做一做
如图,某市为庆祝“两会”召开,在甲建筑物上的A点到E点挂一长20米的宣传条幅,某人在乙建筑物顶部D点测得条幅顶端A点的仰角为 45°,测得此条幅底端E点的俯角为30°,求BC的长
A
E
D
C
B
如图:大楼高30米,远处有一灯塔BC,小明在楼底A处测的塔顶的仰角为45度,爬到楼顶D测的塔顶的仰角30度,求塔高BC及大楼与灯塔之间的距离
A
D
B
E
C
达标检测
A
B
C
在山脚C处测得山顶A的仰角为450。问题如下:
沿着坡角为30 °的斜坡前进300米到达D点,在D点测得山顶A的仰角为600 ,求山高AB。
30°
D
E
F
x
x
动 手 做 一 做
1、一架飞机以300角俯冲400米,
则飞机的高度变化情况是( )
A.升高400米
B.下降400米
C.下降200米
D.下降 米
2、在山顶上D处有一铁塔,在塔顶B处测得 地面上一点A的俯角α=60o,在塔底D测得点A的俯角β=45o,已知塔高BD=30米,
则山高 CD=__________米.
A
B
C
D
α
β
C
本节课你有什么收获
1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。
2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
已知斜边求直边,
已知直边求直边,
已知两边求一边,
已知两边求一角,
已知锐角求锐角,
已知直边求斜边,
计算方法要选择,
正弦余弦很方便;
正切余切理当然;
函数关系要选好;
勾股定理最方便;
互余关系要记好;
用除还需正余弦;
能用乘法不用除.
优选关系式
求山高或建筑物的高;测量河的宽度或物体的长度;航行航海问题等.解决这类问题的关键是先画出测量示意图,把实际问题转化为数学问题,利用直角三角形中角、边之间的数量关系求出所要求的距离或角度.
应用解直角三角形知识解应用题时,可按以下思维过程进行:
(1)画出测量示意图;
(2)寻找直角三角形,若找不到,可构造;
(3) 解直角三角形,若不可直接求解,利用题中的数 量关系,设x求解.
方法归纳
