1.1.3 等腰三角形 课件 (共19张PPT)
文档属性
| 名称 | 1.1.3 等腰三角形 课件 (共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 19:29:05 | ||
图片预览



文档简介
第1节 等腰三角形
(第3课时)
第一章 三角形的证明
2020-2021北师大版八年级数学下册
1 学会证明等角对等边进行等腰三角形的判定;(重点)
2 体会反证法的含义并会用反证法进行证明.(难点)
学习目标
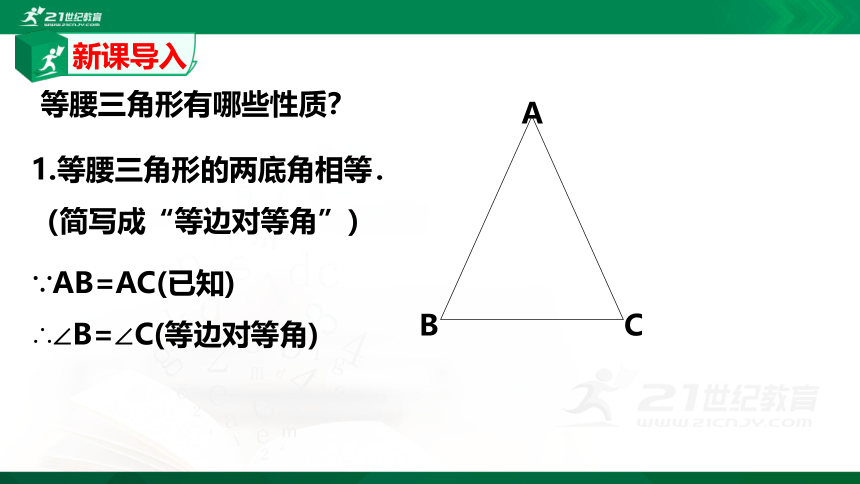
1.等腰三角形的两底角相等.
(简写成“等边对等角”)
A
B
C
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
等腰三角形有哪些性质?
新课导入
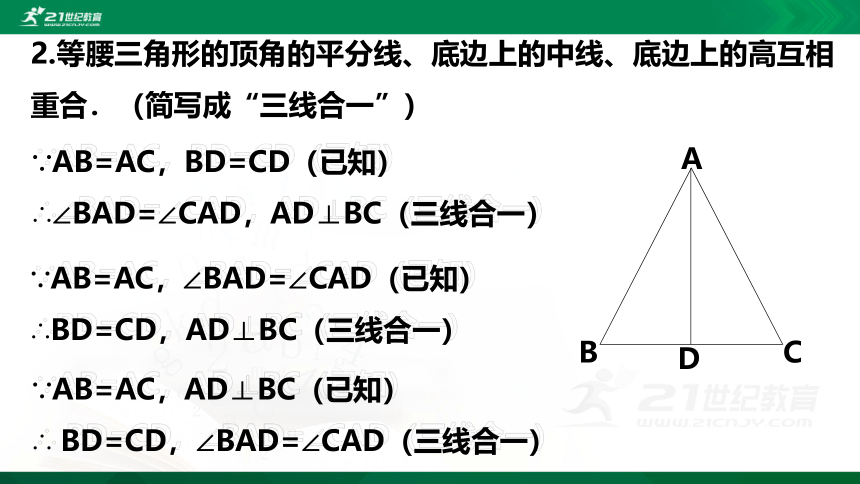
2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.(简写成“三线合一”)
A
B
C
D
∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,AD⊥BC(三线合一)
∵AB=AC,∠BAD=∠CAD(已知)
∴BD=CD,AD⊥BC(三线合一)
∵AB=AC,AD⊥BC(已知)
∴ BD=CD,∠BAD=∠CAD(三线合一)
等腰三角形的判定
知识点一
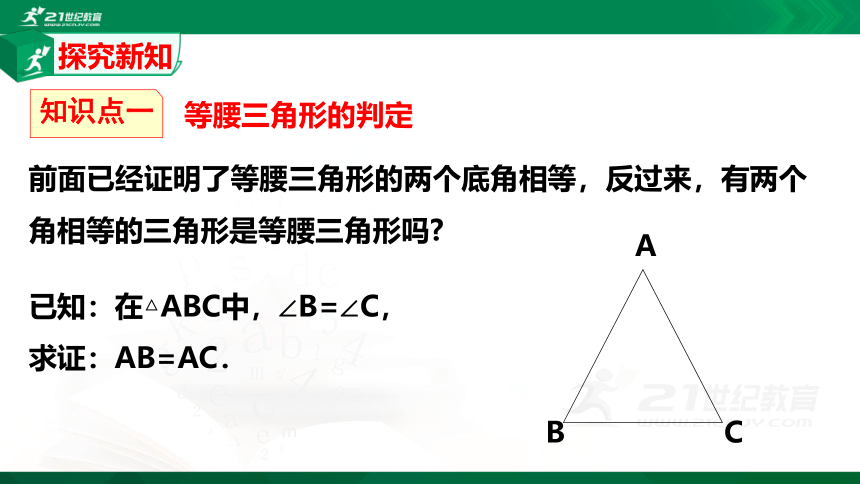
前面已经证明了等腰三角形的两个底角相等,反过来,有两个角相等的三角形是等腰三角形吗?
已知:在△ABC中,∠B=∠C,
求证:AB=AC.
A
B
C
探究新知
A
B
C
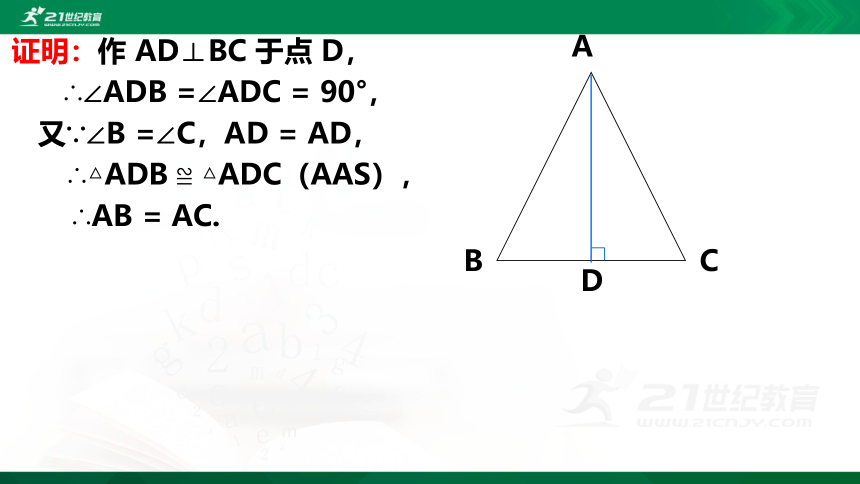
证明:作 AD⊥BC 于点 D,
∴∠ADB =∠ADC = 90°,
又∵∠B =∠C,AD = AD,
∴△ADB ≌ △ADC(AAS),
∴AB = AC.
D
有两个角相等的三角形是等腰三角形.(等角对等边)
等腰三角形的判定定理:
符号语言:在△ABC中,∵∠B=∠C, ∴AB=AC.
等腰三角形的判定与性质的异同
相同点:都是在一个三角形中;
区别:判定是由角到边,性质是由边到角.
即:
例1 已知:如图,AB=DC,BD=CA,
求证:△AED是等腰三角形。
A
B
C
D
E
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS)
∴∠ADB=∠DAC(全等三角形的对应角相等)
∴AE=DE(等角对等边)
∴ △AED是等腰三角形。
例题讲解
想一想
小明认为,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等. 你认为这个结论成立吗?如果成立,你能证明它吗?
A
B
C
反证法
知识点二
A
B
C
如图,在△ABC 中,已知∠B ≠∠C,此时 AB 与 AC 要么相等,要么不相等.
假设 AB = AC,那么根据“等边对等角”定理可得∠C =∠B,这与已知条件∠B ≠∠C 相矛盾,因此 AB ≠ AC.
反证法:先假设命题的结论不成立,然后推导出与定义、基本事实或已知条件相矛盾的结果,从而证明命题的结论一定成立.我们把它叫做反证法.
反证法是一种重要的数学证明方法.在解决某些问题时常常会有出人意料的作用.
2.利用反证法解题的一般步骤:
(1)假设;
(2)归谬:从假设出发,经过推理论证得出与已知、定理、公理等相矛盾的结果;
(3)结论:肯定命题结论正确.
例2 用反证法证明:一个三角形中不能有两个角是直角.
已知:△ABC.
求证:∠A、∠B、∠C中不能有两个角是直角.
证明:假设∠A,∠B,∠C中有两个角是直角,不妨设
∠A和∠B是 直角,即 ∠A= 90°,∠B = 90°.
于是∠A+∠B+∠C=90°+90°+∠C >180°.
这与三角形内角和定理相矛盾,因此“∠A和∠B是直角”的假设不成立. 所以,一个三角形中不能有两个角是直角.
例题讲解
1 在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A.∠A=50°,∠B=70°
B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90°
D.∠A=80°,∠B=60°
课堂练习
2 如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形有( )
A.3个
B.4个
C.5个
D.6个
3 用反证法证明“一个三角形中至多有一个钝角”时,应假设( )
A.一个三角形中至少有两个钝角
B.一个三角形中至多有一个钝角
C.一个三角形中至少有一个钝角
D.一个三角形中没有钝角
4 已知:如图,∠CAE 是△ABC 的外角, AD∥BC 且∠1 =∠2.求证:AB = AC.
1 等腰三角形的判定:
(1)有两边相等的三角形是等腰三角形;
(2)有两个角相等的三角形是等腰三角形.
2 利用反证法解题的一般步骤:
(1) 假设;
(2) 归谬:从假设出发,经过推理论证得出与已知、定理、公理等相矛盾的结果;
(3) 结论:肯定命题结论正确.
课堂小结
谢谢聆听
(第3课时)
第一章 三角形的证明
2020-2021北师大版八年级数学下册
1 学会证明等角对等边进行等腰三角形的判定;(重点)
2 体会反证法的含义并会用反证法进行证明.(难点)
学习目标
1.等腰三角形的两底角相等.
(简写成“等边对等角”)
A
B
C
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
等腰三角形有哪些性质?
新课导入
2.等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.(简写成“三线合一”)
A
B
C
D
∵AB=AC,BD=CD(已知)
∴∠BAD=∠CAD,AD⊥BC(三线合一)
∵AB=AC,∠BAD=∠CAD(已知)
∴BD=CD,AD⊥BC(三线合一)
∵AB=AC,AD⊥BC(已知)
∴ BD=CD,∠BAD=∠CAD(三线合一)
等腰三角形的判定
知识点一
前面已经证明了等腰三角形的两个底角相等,反过来,有两个角相等的三角形是等腰三角形吗?
已知:在△ABC中,∠B=∠C,
求证:AB=AC.
A
B
C
探究新知
A
B
C
证明:作 AD⊥BC 于点 D,
∴∠ADB =∠ADC = 90°,
又∵∠B =∠C,AD = AD,
∴△ADB ≌ △ADC(AAS),
∴AB = AC.
D
有两个角相等的三角形是等腰三角形.(等角对等边)
等腰三角形的判定定理:
符号语言:在△ABC中,∵∠B=∠C, ∴AB=AC.
等腰三角形的判定与性质的异同
相同点:都是在一个三角形中;
区别:判定是由角到边,性质是由边到角.
即:
例1 已知:如图,AB=DC,BD=CA,
求证:△AED是等腰三角形。
A
B
C
D
E
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS)
∴∠ADB=∠DAC(全等三角形的对应角相等)
∴AE=DE(等角对等边)
∴ △AED是等腰三角形。
例题讲解
想一想
小明认为,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等. 你认为这个结论成立吗?如果成立,你能证明它吗?
A
B
C
反证法
知识点二
A
B
C
如图,在△ABC 中,已知∠B ≠∠C,此时 AB 与 AC 要么相等,要么不相等.
假设 AB = AC,那么根据“等边对等角”定理可得∠C =∠B,这与已知条件∠B ≠∠C 相矛盾,因此 AB ≠ AC.
反证法:先假设命题的结论不成立,然后推导出与定义、基本事实或已知条件相矛盾的结果,从而证明命题的结论一定成立.我们把它叫做反证法.
反证法是一种重要的数学证明方法.在解决某些问题时常常会有出人意料的作用.
2.利用反证法解题的一般步骤:
(1)假设;
(2)归谬:从假设出发,经过推理论证得出与已知、定理、公理等相矛盾的结果;
(3)结论:肯定命题结论正确.
例2 用反证法证明:一个三角形中不能有两个角是直角.
已知:△ABC.
求证:∠A、∠B、∠C中不能有两个角是直角.
证明:假设∠A,∠B,∠C中有两个角是直角,不妨设
∠A和∠B是 直角,即 ∠A= 90°,∠B = 90°.
于是∠A+∠B+∠C=90°+90°+∠C >180°.
这与三角形内角和定理相矛盾,因此“∠A和∠B是直角”的假设不成立. 所以,一个三角形中不能有两个角是直角.
例题讲解
1 在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A.∠A=50°,∠B=70°
B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90°
D.∠A=80°,∠B=60°
课堂练习
2 如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形有( )
A.3个
B.4个
C.5个
D.6个
3 用反证法证明“一个三角形中至多有一个钝角”时,应假设( )
A.一个三角形中至少有两个钝角
B.一个三角形中至多有一个钝角
C.一个三角形中至少有一个钝角
D.一个三角形中没有钝角
4 已知:如图,∠CAE 是△ABC 的外角, AD∥BC 且∠1 =∠2.求证:AB = AC.
1 等腰三角形的判定:
(1)有两边相等的三角形是等腰三角形;
(2)有两个角相等的三角形是等腰三角形.
2 利用反证法解题的一般步骤:
(1) 假设;
(2) 归谬:从假设出发,经过推理论证得出与已知、定理、公理等相矛盾的结果;
(3) 结论:肯定命题结论正确.
课堂小结
谢谢聆听
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
