第五章 相交线与平行线章节复习-人教版2020-2021学年七年级数学下册教学课件(共28张ppt)
文档属性
| 名称 | 第五章 相交线与平行线章节复习-人教版2020-2021学年七年级数学下册教学课件(共28张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 07:32:57 | ||
图片预览






文档简介
人教版 七年级数学下册
第五章 相交线与平行线
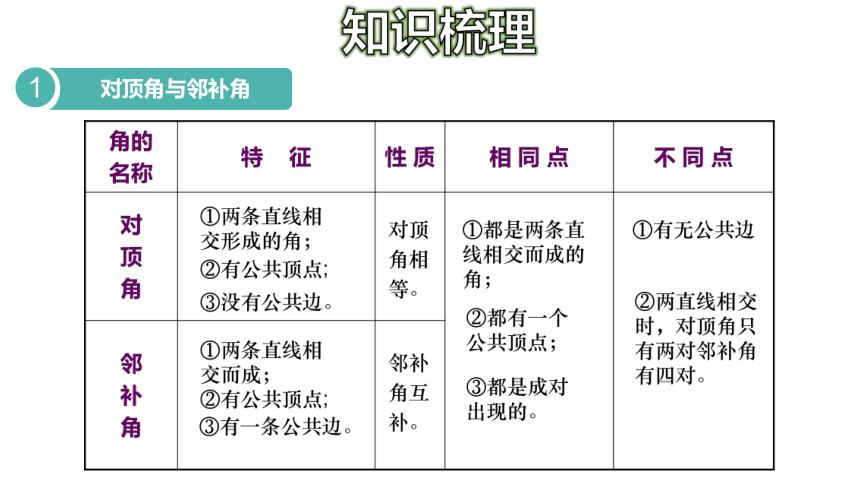
知识梳理
对顶角与邻补角
1
知识梳理
垂线的性质1:过一点有且只有一条直线与已知直线垂直。
垂直:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直;其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
垂线的定义及性质
2
连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:垂线段最短。
垂线的性质2:
知识梳理
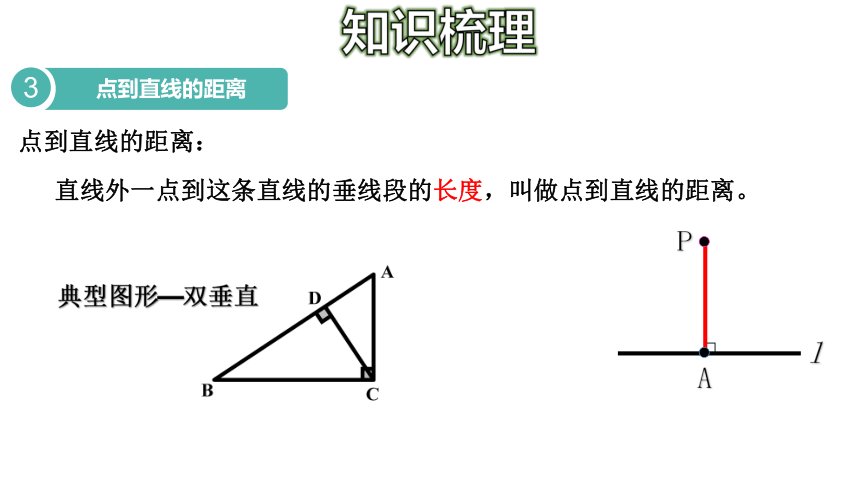
点到直线的距离
3
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
点到直线的距离:
P
l
A
典型图形—双垂直
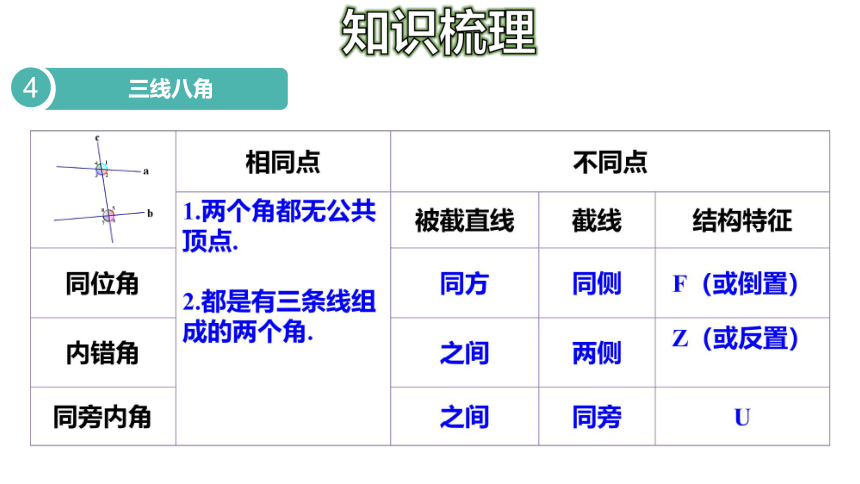
知识梳理
三线八角
4
知识梳理
平行公理及推论
5
平行线的定义:
在同一平面内,不相交的两条直线叫做平行线。
※在同一平面内的两条直线的位置关系有相交或平行两种。
※平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
※平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
知识梳理
平行线的判定方法
6
判定方法1两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
判定方法2两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
简单说成:同旁内角互补,两直线平行。
判定方法3两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
知识梳理
平行线的判定方法
7
性质1两直线平行,同位角相等.
性质2两直线平行,内错角相等.
性质3两直线平行,同旁内角互补.
知识梳理
命题、定理、证明
8
★命题的定义:判定一件事情的语句,叫做命题。
★命题的构成:命题由题设和结论组成。题设是已知项,结论是由已知项推出的事项.
★命题的书写形式
数学中的命题常可以写成“如果……那么……”的形式,这时“如果”后接的部分是题设,“那么”后接的部分是结论.
★命题的分类
真命题:如果题设成立,那么结论一定成立,这样的命题叫做真命题.
假命题:如果题设成立时,不能保证结论一定成立,这样的命题叫做假命题.
★定理的概念:一些命题的正确性是经过推理证实的,这样得到的真命题叫做定理.
★证明的概念:一个命题的正确性需要经过推理,才能作出判断,这个推理过程叫做证明.
知识梳理
平移定义及性质、作图
9
1. 平移的定义:“三要素”
一个图形、一个方向、一个距离。
2. 平移的性质:“四特征”
图形的形状和大小不改变;
对应点所连的线段平行(或在一条直线上)且相等;
对应线段平行(或在一条直线上)且相等;
对应角相等.
知识梳理
平移定义及性质、作图
9
平移作图的一般步骤:
平移作图是平移性质的应用,利用平移可以得到许多美
丽的图案,在具体作图时,应分四步——定、找、移、连。
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图顺次连接对应点.
考点解析
【例1】如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,求∠DOF的度数.
B
A
C
D
F
E
O
解:
∵AB⊥CD,
∴∠AOC=90°
∵∠AOE=65°
∴∠COE=25°
又∵∠COE=∠DOF(对顶角相等)
∴∠DOF=25°
01
相交线相关求角度问题
【点睛】两条直线相交包括垂直和斜交两种情形.相交时形成了两对对顶角和四对邻补角.其中垂直是相交的特殊情况,它将一个周角分成了四个直角.
迁移应用
【迁移应用】如图,AB,CD相交于点O,∠AOC=70°,EF平分∠COB,求∠COE的度数.
A
B
C
D
E
F
O
01
相交线相关求角度问题
解:
∵ ∠AOC=70°
∴∠COB=180°- ∠AOC = 180°- 70°=110°
∵ EF平分∠COB ,
∴∠AOB=12∠????????????= 12× 110°=55°
又∵∠AOE=∠ AOB(对顶角相等)
∵∠AOE =55°
∴ ∠COE=∠AOE + ∠AOC=55°+70°=125°
?
02
点到直线的距离辨析
【例2】如图,AD为三角形ABC的高,能表示点到直线(线段)的距离的线段有( )
A.2条 B.3条 C.4条 D.5条
【点睛】直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.寻找技巧:1.确定垂线段;2.垂足所在直线为“这条直线”;3.另一端点即是“直线外一点”.
B
C
D
A
B
考点解析
【迁移应用】如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,AC=6cm,BC=8cm,则点C到AB的距离是 cm;点A到BC的距离是 cm;点B到AC的距离是___cm.
4.8
6
8
02
点到直线的距离辨析
迁移应用
考点解析
03
平行线的性质和判定
【例3】(1)如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
解:∵∠1=∠2=72°
∴a//b (内错角相等,两直线平行)
∴∠3+∠4=180° (两直线平行,同旁内角互补)
∵∠3=60°
∴∠4=120°
a
b
考点解析
03
平行线的性质和判定
证明: ∵∠DAC= ∠ACB (已知)
∴ AD//BC(内错角相等,两直线平行)
∵ ∠D+∠DFE=180°(已知)
∴ AD// EF(同旁内角互补,两直线平行)
∴ EF// BC(平行于同一条直线的两条直线互相平行)
(2)已知∠DAC=∠ACB,∠D+∠DFE=180°,求证:EF//BC.
A
B
C
D
E
F
【点睛】平行线的性质和判定经常结合使用,由角之间的关系得出直线平行,进而再得出其他角之间的关系,或是由直线平行得到角之间的关系,进而再由角的关系得出其他直线平行.
03
平行线的性质和判定
迁移应用
【迁移应用】如图:BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H.∠GFH+∠BHC=180°,求证:∠1=∠2.
解:∵∠BHC=∠FHD,∠GFH+∠BHC=180°(已知)
∴∠GFH+∠FHD=180°(等量代换)
∴FG∥ BD(同旁内角互补,两直线平行)
∴∠1=∠ABD(两直线平行,同位角相等)
∵BD平分∠ABC(已知)
∴∠2=∠ABD(角平分线的定义)
∴∠1=∠2(等量代换)
考点解析
04
平移变换性质应用
【例4】如图所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是 ( )
D
【点睛】抓住平移前后的图形形状和大小完全相同,任何一对对应点连线段平行(或共线)且相等的性质解题.
04
平移变换性质应用
迁移应用
【迁移应用】如图所示,△DEF经过平移得到△ABC, 那么∠C的对应角和ED的对应边分别是 ( )
A.∠F, AC
B.∠BOD, BA
C.∠F, BA
D.∠BOD, AC
C
05
相交线中的方程思想
解:设∠1的度数为x°,则∠2的度数为x°,
∠3的度数为8x°,根据题意可得
x°+x°+8x°=180°,解得x=18.
即∠1=∠2=18°,
而∠4=∠1+∠2(对顶角相等).
故∠4=36°.
【例5】如图所示, 交于点O,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数.
)
)
)
)
1
2
3
4
O
【点睛】当题干中出现“角之间的倍数关系或是比值”通常利用方程解决问题。这是几何与代数知识相结合的一种体现,它可以使解题思路清晰,过程简便.在有关线段或角的求值问题中它的应用非常广泛.
考点解析
05
相交线中的方程思想
迁移应用
【迁移应用】如图,直线AB,CD相交于点0,已知∠AOC=70°,OE把∠BOD分成两个角,且∠BOE:∠DOE=2:3,求∠DOE的度数..
解:∵∠AOC=70°
∴∠BOD=∠AOC=70°
∵∠BOE:∠EOD=2:3
设∠BOE=2x,∠EOD=3x
∴ 2x+3x= 70°
∴x=14°
∴∠DOE= 3x=42°
考点解析
06
平行线间“拐点”问题
【例6】如图,直线l1∥ l2,∠α=∠β,∠1=40°,则∠2=______.
A
B
C
D
解:延长CD交直线l2于点E
∵l1∥ l2
∴∠3=∠1=40°
∵∠α=∠β
∴AB∥ CD
∴∠2+∠3=180°
∴∠2=180°-∠3=180°-40°=140°
E
140°
考点解析
06
平行线间“拐点”问题
【迁移应用】如图,AB∥ CD,试说明∠B、∠D 、∠BED之间的大小关系.
A
B
C
D
E
F
解:∠B+∠BED=∠D。
理由:过点E作EF∥ AB
∵AB∥ CD, EF∥ AB (已知)
∴AB∥ CD∥ EF(平面内两条直线都与同一条
直线平行,这两条直线互相平行)
∴∠B=∠BEF,∠D=∠DEF(两直线平行,内错角相等)
∵∠BEF+ ∠BED =∠DEF
∴ ∠B+∠BED=∠D
若AB∥CD, 则∠ =∠ .
1.如图, 若∠3=∠4,则 ∥ ;
AD
1
2
2.如图,∠D=70°,∠C= 110°,∠1=69°,则∠B=_____.
B
A
C
E
D
⌒
1
69°
BC
⌒
⌒
⌒
⌒
C
D
1
4
3
2
A
B
达标检测
3.如图1,已知 AB∥CD, ∠1=30°, ∠2=90°,则∠3= °
4.如图2,若AE∥CD, ∠EBF=135°,∠BFD=60°,∠D=( )
A.75° B.45° C.30° D.15°
图1
图2
60
D
达标检测
5.如图,直线AB、CD、EF相交于点O,OG平分∠COF,∠1=30°,∠2=45°,求∠3的度数.
解:∵∠1=30°,∠2=45°
∴∠EOD=180°-∠1-∠2=105°
∴∠COF=∠EOD=105°
又∵OG平分∠COF
∴∠3=12∠COF=52.5°
?
达标检测
6.如图,A、B、C和D、E、F分别在同一直线上,∠1=∠2,∠C=∠F,求证:∠A=∠D.
证明:∵∠1=∠2,∠2=∠3
∴∠1=∠3
∴BF∥CE(同位角相等,两直线平行
∴∠4=∠C(两直线平行,同位角相等)
∵∠C=∠F
∴∠4=∠F
∴DF∥AC(内错角相等,两直线平行)
∴∠A=∠D(两直线平行,内错角相等)
达标检测
第五章 相交线与平行线
知识梳理
对顶角与邻补角
1
知识梳理
垂线的性质1:过一点有且只有一条直线与已知直线垂直。
垂直:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直;其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
垂线的定义及性质
2
连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:垂线段最短。
垂线的性质2:
知识梳理
点到直线的距离
3
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
点到直线的距离:
P
l
A
典型图形—双垂直
知识梳理
三线八角
4
知识梳理
平行公理及推论
5
平行线的定义:
在同一平面内,不相交的两条直线叫做平行线。
※在同一平面内的两条直线的位置关系有相交或平行两种。
※平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
※平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
知识梳理
平行线的判定方法
6
判定方法1两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
判定方法2两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
简单说成:同旁内角互补,两直线平行。
判定方法3两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
知识梳理
平行线的判定方法
7
性质1两直线平行,同位角相等.
性质2两直线平行,内错角相等.
性质3两直线平行,同旁内角互补.
知识梳理
命题、定理、证明
8
★命题的定义:判定一件事情的语句,叫做命题。
★命题的构成:命题由题设和结论组成。题设是已知项,结论是由已知项推出的事项.
★命题的书写形式
数学中的命题常可以写成“如果……那么……”的形式,这时“如果”后接的部分是题设,“那么”后接的部分是结论.
★命题的分类
真命题:如果题设成立,那么结论一定成立,这样的命题叫做真命题.
假命题:如果题设成立时,不能保证结论一定成立,这样的命题叫做假命题.
★定理的概念:一些命题的正确性是经过推理证实的,这样得到的真命题叫做定理.
★证明的概念:一个命题的正确性需要经过推理,才能作出判断,这个推理过程叫做证明.
知识梳理
平移定义及性质、作图
9
1. 平移的定义:“三要素”
一个图形、一个方向、一个距离。
2. 平移的性质:“四特征”
图形的形状和大小不改变;
对应点所连的线段平行(或在一条直线上)且相等;
对应线段平行(或在一条直线上)且相等;
对应角相等.
知识梳理
平移定义及性质、作图
9
平移作图的一般步骤:
平移作图是平移性质的应用,利用平移可以得到许多美
丽的图案,在具体作图时,应分四步——定、找、移、连。
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图顺次连接对应点.
考点解析
【例1】如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,求∠DOF的度数.
B
A
C
D
F
E
O
解:
∵AB⊥CD,
∴∠AOC=90°
∵∠AOE=65°
∴∠COE=25°
又∵∠COE=∠DOF(对顶角相等)
∴∠DOF=25°
01
相交线相关求角度问题
【点睛】两条直线相交包括垂直和斜交两种情形.相交时形成了两对对顶角和四对邻补角.其中垂直是相交的特殊情况,它将一个周角分成了四个直角.
迁移应用
【迁移应用】如图,AB,CD相交于点O,∠AOC=70°,EF平分∠COB,求∠COE的度数.
A
B
C
D
E
F
O
01
相交线相关求角度问题
解:
∵ ∠AOC=70°
∴∠COB=180°- ∠AOC = 180°- 70°=110°
∵ EF平分∠COB ,
∴∠AOB=12∠????????????= 12× 110°=55°
又∵∠AOE=∠ AOB(对顶角相等)
∵∠AOE =55°
∴ ∠COE=∠AOE + ∠AOC=55°+70°=125°
?
02
点到直线的距离辨析
【例2】如图,AD为三角形ABC的高,能表示点到直线(线段)的距离的线段有( )
A.2条 B.3条 C.4条 D.5条
【点睛】直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.寻找技巧:1.确定垂线段;2.垂足所在直线为“这条直线”;3.另一端点即是“直线外一点”.
B
C
D
A
B
考点解析
【迁移应用】如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,AC=6cm,BC=8cm,则点C到AB的距离是 cm;点A到BC的距离是 cm;点B到AC的距离是___cm.
4.8
6
8
02
点到直线的距离辨析
迁移应用
考点解析
03
平行线的性质和判定
【例3】(1)如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
解:∵∠1=∠2=72°
∴a//b (内错角相等,两直线平行)
∴∠3+∠4=180° (两直线平行,同旁内角互补)
∵∠3=60°
∴∠4=120°
a
b
考点解析
03
平行线的性质和判定
证明: ∵∠DAC= ∠ACB (已知)
∴ AD//BC(内错角相等,两直线平行)
∵ ∠D+∠DFE=180°(已知)
∴ AD// EF(同旁内角互补,两直线平行)
∴ EF// BC(平行于同一条直线的两条直线互相平行)
(2)已知∠DAC=∠ACB,∠D+∠DFE=180°,求证:EF//BC.
A
B
C
D
E
F
【点睛】平行线的性质和判定经常结合使用,由角之间的关系得出直线平行,进而再得出其他角之间的关系,或是由直线平行得到角之间的关系,进而再由角的关系得出其他直线平行.
03
平行线的性质和判定
迁移应用
【迁移应用】如图:BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H.∠GFH+∠BHC=180°,求证:∠1=∠2.
解:∵∠BHC=∠FHD,∠GFH+∠BHC=180°(已知)
∴∠GFH+∠FHD=180°(等量代换)
∴FG∥ BD(同旁内角互补,两直线平行)
∴∠1=∠ABD(两直线平行,同位角相等)
∵BD平分∠ABC(已知)
∴∠2=∠ABD(角平分线的定义)
∴∠1=∠2(等量代换)
考点解析
04
平移变换性质应用
【例4】如图所示,下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是 ( )
D
【点睛】抓住平移前后的图形形状和大小完全相同,任何一对对应点连线段平行(或共线)且相等的性质解题.
04
平移变换性质应用
迁移应用
【迁移应用】如图所示,△DEF经过平移得到△ABC, 那么∠C的对应角和ED的对应边分别是 ( )
A.∠F, AC
B.∠BOD, BA
C.∠F, BA
D.∠BOD, AC
C
05
相交线中的方程思想
解:设∠1的度数为x°,则∠2的度数为x°,
∠3的度数为8x°,根据题意可得
x°+x°+8x°=180°,解得x=18.
即∠1=∠2=18°,
而∠4=∠1+∠2(对顶角相等).
故∠4=36°.
【例5】如图所示, 交于点O,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数.
)
)
)
)
1
2
3
4
O
【点睛】当题干中出现“角之间的倍数关系或是比值”通常利用方程解决问题。这是几何与代数知识相结合的一种体现,它可以使解题思路清晰,过程简便.在有关线段或角的求值问题中它的应用非常广泛.
考点解析
05
相交线中的方程思想
迁移应用
【迁移应用】如图,直线AB,CD相交于点0,已知∠AOC=70°,OE把∠BOD分成两个角,且∠BOE:∠DOE=2:3,求∠DOE的度数..
解:∵∠AOC=70°
∴∠BOD=∠AOC=70°
∵∠BOE:∠EOD=2:3
设∠BOE=2x,∠EOD=3x
∴ 2x+3x= 70°
∴x=14°
∴∠DOE= 3x=42°
考点解析
06
平行线间“拐点”问题
【例6】如图,直线l1∥ l2,∠α=∠β,∠1=40°,则∠2=______.
A
B
C
D
解:延长CD交直线l2于点E
∵l1∥ l2
∴∠3=∠1=40°
∵∠α=∠β
∴AB∥ CD
∴∠2+∠3=180°
∴∠2=180°-∠3=180°-40°=140°
E
140°
考点解析
06
平行线间“拐点”问题
【迁移应用】如图,AB∥ CD,试说明∠B、∠D 、∠BED之间的大小关系.
A
B
C
D
E
F
解:∠B+∠BED=∠D。
理由:过点E作EF∥ AB
∵AB∥ CD, EF∥ AB (已知)
∴AB∥ CD∥ EF(平面内两条直线都与同一条
直线平行,这两条直线互相平行)
∴∠B=∠BEF,∠D=∠DEF(两直线平行,内错角相等)
∵∠BEF+ ∠BED =∠DEF
∴ ∠B+∠BED=∠D
若AB∥CD, 则∠ =∠ .
1.如图, 若∠3=∠4,则 ∥ ;
AD
1
2
2.如图,∠D=70°,∠C= 110°,∠1=69°,则∠B=_____.
B
A
C
E
D
⌒
1
69°
BC
⌒
⌒
⌒
⌒
C
D
1
4
3
2
A
B
达标检测
3.如图1,已知 AB∥CD, ∠1=30°, ∠2=90°,则∠3= °
4.如图2,若AE∥CD, ∠EBF=135°,∠BFD=60°,∠D=( )
A.75° B.45° C.30° D.15°
图1
图2
60
D
达标检测
5.如图,直线AB、CD、EF相交于点O,OG平分∠COF,∠1=30°,∠2=45°,求∠3的度数.
解:∵∠1=30°,∠2=45°
∴∠EOD=180°-∠1-∠2=105°
∴∠COF=∠EOD=105°
又∵OG平分∠COF
∴∠3=12∠COF=52.5°
?
达标检测
6.如图,A、B、C和D、E、F分别在同一直线上,∠1=∠2,∠C=∠F,求证:∠A=∠D.
证明:∵∠1=∠2,∠2=∠3
∴∠1=∠3
∴BF∥CE(同位角相等,两直线平行
∴∠4=∠C(两直线平行,同位角相等)
∵∠C=∠F
∴∠4=∠F
∴DF∥AC(内错角相等,两直线平行)
∴∠A=∠D(两直线平行,内错角相等)
达标检测
