5.1.3 同位角、内错角、同旁内角跟踪练习(含答案)
文档属性
| 名称 | 5.1.3 同位角、内错角、同旁内角跟踪练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 14:21:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.1.3 同位角、内错角、同旁内角跟踪练习
一、单选题(共10小题)
1.(2020·云南怒江傈僳族自治州·七年级期末)如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( )
A.∠4,∠2 B.∠2,∠6 C.∠5,∠4 D.∠2,∠4
2.(2020·湖北恩施土家族苗族自治州·七年级期中)如图,∠B的同位角可以是
A.∠1 B.∠2 C.∠3 D.∠4
3.(2020·四川成都市·七年级期末)如图,直线a,b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
4.(2020·山西晋中市·七年级期中)如图,描述同位角、内错角、同旁内角关系不正确的是( )
A.与是同位角 B.与是内错角
C.与是同旁内角 D.与是同旁内角
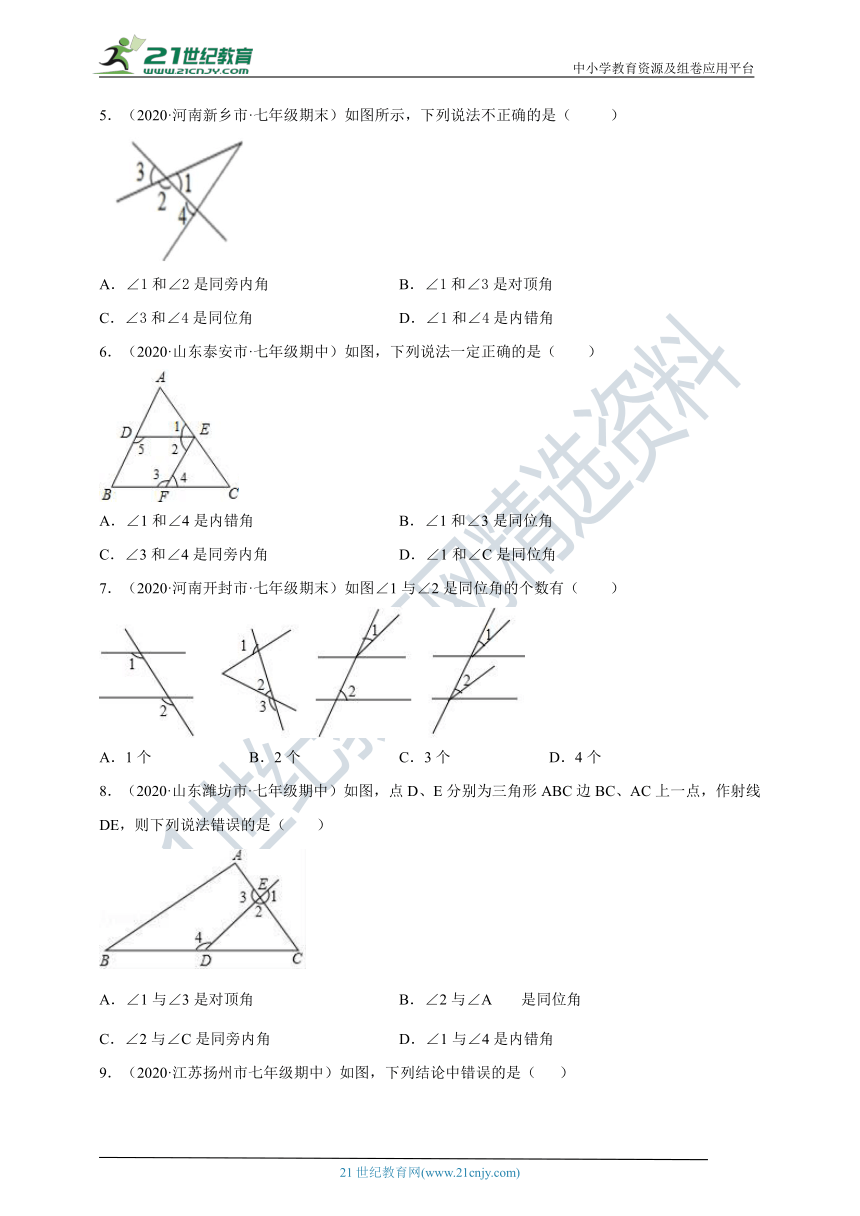
5.(2020·河南新乡市·七年级期末)如图所示,下列说法不正确的是( )
A.∠1和∠2是同旁内角 B.∠1和∠3是对顶角
C.∠3和∠4是同位角 D.∠1和∠4是内错角
6.(2020·山东泰安市·七年级期中)如图,下列说法一定正确的是( )
A.∠1和∠4是内错角 B.∠1和∠3是同位角
C.∠3和∠4是同旁内角 D.∠1和∠C是同位角
7.(2020·河南开封市·七年级期末)如图∠1与∠2是同位角的个数有( )
A.1个 B.2个 C.3个 D.4个
8.(2020·山东潍坊市·七年级期中)如图,点D、E分别为三角形ABC边BC、AC上一点,作射线DE,则下列说法错误的是( )
A.∠1与∠3是对顶角 B.∠2与∠A是同位角
C.∠2与∠C是同旁内角 D.∠1与∠4是内错角
9.(2020·江苏扬州市七年级期中)如图,下列结论中错误的是( )
A.与是同旁内角 B.与是内错角
C.与是内错角 D.与是同位角
10.(2020·甘南县八一学校七年级期末)如图,直线a,b被直线c所截,则下列说法中错误的是( )
A.∠1与∠2是邻补角 B.∠1与∠3是对顶角
C.∠2与∠4是同位角 D.∠3与∠4是内错角
二、填空题(共5小题)
11.(2020·广东茂名市·七年级期中)如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于______,∠3的内错角等于______,∠3的同旁内角等于______.
12.(2020·古田县七年级期中)如图,按角的位置关系填空:∠A与∠1是______;∠A与∠3是______;∠2与∠3是______.
13.(2020·贵州毕节市·七年级期末)如图,∠1和∠2是________角,∠2和∠3是________角.
14.(2020·定兴县七年级期末)如图,直线 被直线所截, 和__________是同位角, 和__________是内错角
15.(2020·石嘴山市七年级期中)如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是______(填序号).
三、解答题(共3小题)
16.(2020·广东阳江市·七年级期末)两条直线被第三条直线所截,和是同旁内角,和是内错角.
(1)根据上述条件,画出符合题意的示意图;
(2)若、,求,的度数
17.(2020·山西吕梁市·七年级期中)复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线,被直线所截,在这个基本图形中,形成了______对同旁内角.
(2)如图2,平面内三条直线,,两两相交,交点分别为、、,图中一共有______对同旁内角.
(3)平面内四条直线两两相交,最多可以形成______对同旁内角.
(4)平面内条直线两两相交,最多可以形成______对同旁内角.
答案
一、单选题(共10小题)
1.B 2.D 3.C 4.D 5.A 6.D 7.D. 8.D 9.C 10.D
二、填空题(共5小题)
11.【答案】80°;80°;100°
12.【答案】同旁内角 同位角 内错角
13.【答案】同位 同旁内
14.【答案】
15.【答案】①②③
三、解答题(共3小题)
16.【答案】(1)答案见解析;(2)∠1=162°,∠2=54°.
【详解】
解:(1)如图,下图为所求作.
(2),,
,
又,
,
,
,.
17.【答案】(1)2;(2)6;(3)24;(4)
【详解】
(1)如图
其中同旁内角有与,与,共2对
(2)如图
其中同旁内角有与,与,与,与,与,与,共6对,
(3)如图
其中的同位角有与,与,与,与,与,与,与,与,与,与,与,与,与,与,与,与, 与,与,与,与,与,与,与,与共24对,
(4)根据以上规律,平面内条直线两两相交,最多可以形成对同旁内角
_21?????????è?????(www.21cnjy.com)_
5.1.3 同位角、内错角、同旁内角跟踪练习
一、单选题(共10小题)
1.(2020·云南怒江傈僳族自治州·七年级期末)如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( )
A.∠4,∠2 B.∠2,∠6 C.∠5,∠4 D.∠2,∠4
2.(2020·湖北恩施土家族苗族自治州·七年级期中)如图,∠B的同位角可以是
A.∠1 B.∠2 C.∠3 D.∠4
3.(2020·四川成都市·七年级期末)如图,直线a,b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
4.(2020·山西晋中市·七年级期中)如图,描述同位角、内错角、同旁内角关系不正确的是( )
A.与是同位角 B.与是内错角
C.与是同旁内角 D.与是同旁内角
5.(2020·河南新乡市·七年级期末)如图所示,下列说法不正确的是( )
A.∠1和∠2是同旁内角 B.∠1和∠3是对顶角
C.∠3和∠4是同位角 D.∠1和∠4是内错角
6.(2020·山东泰安市·七年级期中)如图,下列说法一定正确的是( )
A.∠1和∠4是内错角 B.∠1和∠3是同位角
C.∠3和∠4是同旁内角 D.∠1和∠C是同位角
7.(2020·河南开封市·七年级期末)如图∠1与∠2是同位角的个数有( )
A.1个 B.2个 C.3个 D.4个
8.(2020·山东潍坊市·七年级期中)如图,点D、E分别为三角形ABC边BC、AC上一点,作射线DE,则下列说法错误的是( )
A.∠1与∠3是对顶角 B.∠2与∠A是同位角
C.∠2与∠C是同旁内角 D.∠1与∠4是内错角
9.(2020·江苏扬州市七年级期中)如图,下列结论中错误的是( )
A.与是同旁内角 B.与是内错角
C.与是内错角 D.与是同位角
10.(2020·甘南县八一学校七年级期末)如图,直线a,b被直线c所截,则下列说法中错误的是( )
A.∠1与∠2是邻补角 B.∠1与∠3是对顶角
C.∠2与∠4是同位角 D.∠3与∠4是内错角
二、填空题(共5小题)
11.(2020·广东茂名市·七年级期中)如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于______,∠3的内错角等于______,∠3的同旁内角等于______.
12.(2020·古田县七年级期中)如图,按角的位置关系填空:∠A与∠1是______;∠A与∠3是______;∠2与∠3是______.
13.(2020·贵州毕节市·七年级期末)如图,∠1和∠2是________角,∠2和∠3是________角.
14.(2020·定兴县七年级期末)如图,直线 被直线所截, 和__________是同位角, 和__________是内错角
15.(2020·石嘴山市七年级期中)如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是______(填序号).
三、解答题(共3小题)
16.(2020·广东阳江市·七年级期末)两条直线被第三条直线所截,和是同旁内角,和是内错角.
(1)根据上述条件,画出符合题意的示意图;
(2)若、,求,的度数
17.(2020·山西吕梁市·七年级期中)复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线,被直线所截,在这个基本图形中,形成了______对同旁内角.
(2)如图2,平面内三条直线,,两两相交,交点分别为、、,图中一共有______对同旁内角.
(3)平面内四条直线两两相交,最多可以形成______对同旁内角.
(4)平面内条直线两两相交,最多可以形成______对同旁内角.
答案
一、单选题(共10小题)
1.B 2.D 3.C 4.D 5.A 6.D 7.D. 8.D 9.C 10.D
二、填空题(共5小题)
11.【答案】80°;80°;100°
12.【答案】同旁内角 同位角 内错角
13.【答案】同位 同旁内
14.【答案】
15.【答案】①②③
三、解答题(共3小题)
16.【答案】(1)答案见解析;(2)∠1=162°,∠2=54°.
【详解】
解:(1)如图,下图为所求作.
(2),,
,
又,
,
,
,.
17.【答案】(1)2;(2)6;(3)24;(4)
【详解】
(1)如图
其中同旁内角有与,与,共2对
(2)如图
其中同旁内角有与,与,与,与,与,与,共6对,
(3)如图
其中的同位角有与,与,与,与,与,与,与,与,与,与,与,与,与,与,与,与, 与,与,与,与,与,与,与,与共24对,
(4)根据以上规律,平面内条直线两两相交,最多可以形成对同旁内角
_21?????????è?????(www.21cnjy.com)_
