六年级下册数学 一课一练 3.2圆锥 人教版(含答案)
文档属性
| 名称 | 六年级下册数学 一课一练 3.2圆锥 人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 186.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 14:05:37 | ||
图片预览


文档简介
六年级下册数学一课一练-3.2圆锥
一、单选题
1.一个圆锥的体积是18立方分米,比与它等底等高的圆柱的体积少(??? )立方分米。
A.?36?????????????????????????????????????????B.?24?????????????????????????????????????????C.?9?????????????????????????????????????????D.?18?
2.把一个圆柱铸成一个圆锥体,它的(??? )不变。
A.?体积???????????????????????????????????????B.?表面积???????????????????????????????????????C.?侧面积
3.把一支新的圆柱形铅笔削尖,笔尖(圆锥部分)的体积是削去部分的( ??)。
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?2倍
4.一个圆锥的体积是30立方米,和它等底等高的圆柱的体积是(???? )立方米。
A.?30????????????????????????????????????????????B.?10????????????????????????????????????????????C.?90
二、判断题
5.一个圆锥的体积是6立方厘米,那么圆柱的体积是18立方厘米.(? )
6.一个圆锥体的高扩大2倍,底面积缩小2倍,它的体积不变。( )
7.若圆锥的体积是圆柱的 ,那么它们一定是等底等高。(?? )
8.一个圆柱的体积是一个圆锥体积的3倍,那么它们一定等底等高.( ??)
三、填空题
9.一个底面半径4分米,高6分米的圆锥体沙堆,它的体积是________立方分米.
10.一个高45cm的圆锥体容器,盛满水后再倒入和它等底等高的圆柱体容器里,水面的高度是________cm.
11.计算圆锥的体积________.(图中单位:厘米)
四、解答题
12.想一想,画一画。
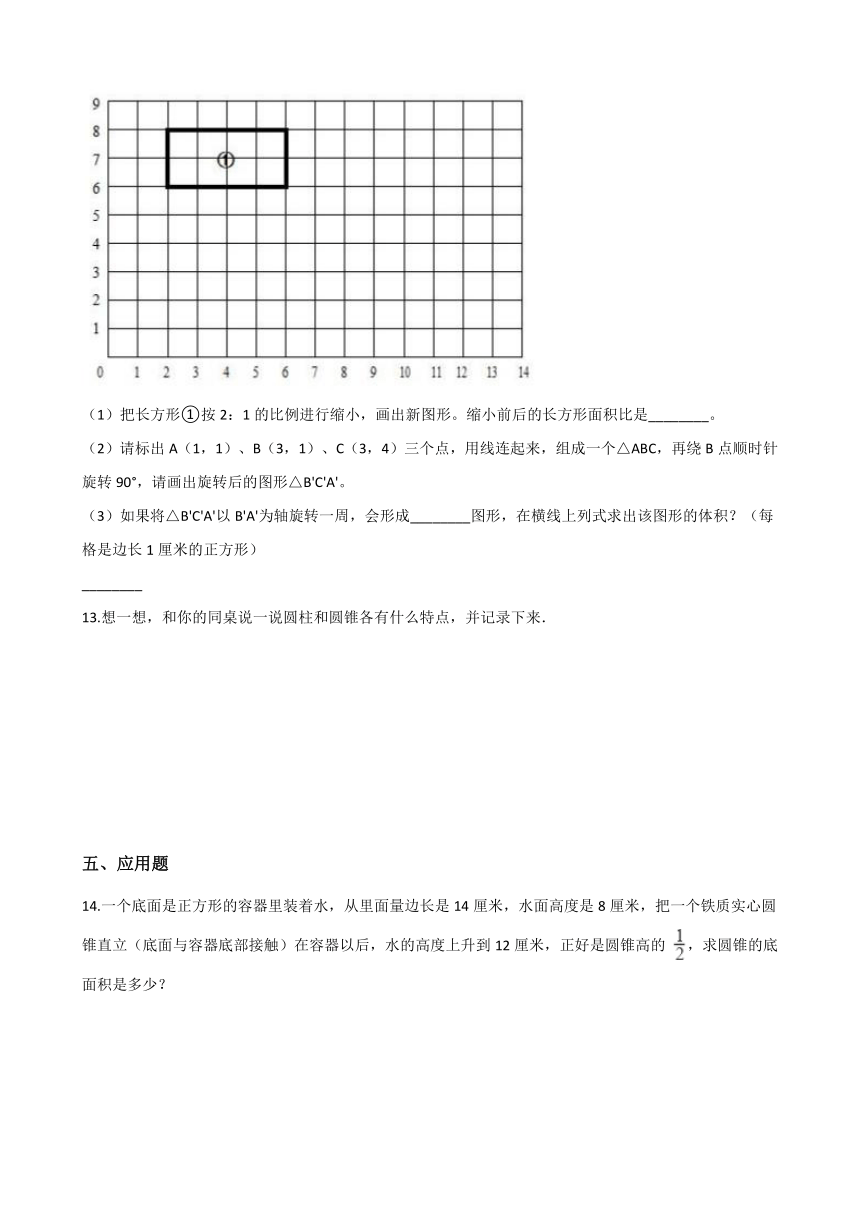
(1)把长方形①按2:1的比例进行缩小,画出新图形。缩小前后的长方形面积比是________。
(2)请标出A(1,1)、B(3,1)、C(3,4)三个点,用线连起来,组成一个△ABC,再绕B点顺时针旋转90°,请画出旋转后的图形△B'C'A'。
(3)如果将△B'C'A'以B'A'为轴旋转一周,会形成________图形,在横线上列式求出该图形的体积?(每格是边长1厘米的正方形)
________
13.想一想,和你的同桌说一说圆柱和圆锥各有什么特点,并记录下来.
五、应用题
14.一个底面是正方形的容器里装着水,从里面量边长是14厘米,水面高度是8厘米,把一个铁质实心圆锥直立(底面与容器底部接触)在容器以后,水的高度上升到12厘米,正好是圆锥高的 ,求圆锥的底面积是多少?
参考答案
一、单选题
1.【答案】A
【解析】【解答】18×3-18
=54-18
=36(立方分米)
故答案为:A.
【分析】等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍,已知圆锥的体积,用圆锥的体积×3=圆柱的体积,然后用减法求出圆锥比圆柱体积少的部分,据此列式解答.
2.【答案】 A
【解析】【解答】 把一个圆柱铸成一个圆锥体,它的体积不变。
故答案为:A。
【分析】此题主要考查了体积的认识,在物体熔铸的过程中,形状会发生变化,体积不变。
3.【答案】 B
【解析】【解答】3–1=2;1÷2=
故答案为:B
【分析】题意可知,把一个圆柱削成一个等底等高的圆锥,圆锥的体积等于和它等底等高圆柱体积的三分之一,即把圆柱体积看作单位“1”平均分成3份,圆锥体积占1份,削去部分占2份, 笔尖(圆锥部分)的体积是削去部分的 。
4.【答案】 C
【解析】【解答】30×3=90(立方米)
答:圆柱的体积是90立方米。
故选:C
【分析】等底等高的圆柱的体积是圆锥体积的3倍,圆锥的体积已知,求圆柱的体积,可用圆锥的体积乘3进行计算即可得到答案。
二、判断题
5.【答案】 错误
【解析】【解答】圆锥和圆柱的底面积和高都不知道,所以它们的体积没有关系,原题说法错误。
故答案为:错误。
【分析】等底等高的圆柱的体积是圆锥体积的3倍,据此解答。
6.【答案】正确
【解析】解答:
分析:由圆锥的体积公式可得。
7.【答案】 错误
【解析】【解答】解:若圆锥的体积是圆柱的, 那么它们不一定等底等高。原题说法错误。
故答案为:错误。
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×, 等底等高的圆锥体积是圆柱的;但是圆锥的体积是圆柱的, 它们不一定等底等高。
8.【答案】 错误
【解析】【解答】因为等底等高的圆柱体的体积是圆锥体体积的3倍,所以如果圆柱体积是圆锥体积的3倍,那么它们的底和高度的乘积是相等的,但是底和高不一定相等,原题说法错误。
故答案为:错误。
【分析】此题主要考查了圆柱和圆锥的体积关系,等底等高的圆柱体的体积是圆锥体体积的3倍,如果圆柱体积是圆锥体积的3倍,那么它们的底和高的乘积是相等的,但是底和高不一定相等,据此判断。
三、填空题
9.【答案】 100.48
【解析】【解答】解:
=
=100.48(立方分米)
答:它的体积是100.48立方分米.
10.【答案】 15
【解析】【解答】45×=15(cm)。
所以倒入圆柱容器中,水面的高度为15cm。
故答案为:15。
【分析】圆柱的体积=底面积×高,圆锥的体积=×底面积×高,本题中水的体积一定即圆柱的体积=圆锥的体积,圆柱与圆锥等底即圆柱与圆锥的底面积相等,即可得出圆柱的高=×圆锥的高。
11.【答案】 75.36立方厘米
【解析】【解答】8÷2=4(厘米)
×3.14×42×4.5
=×3.14×16×4.5
=3.14×16×1.5
=50.24×1.5
=75.36(立方厘米)
故答案为:75.36
【分析】已知圆锥的底面直径和高,求圆锥的体积,先求出圆锥的底面半径,然后用公式:V=πr2h,据此列式解答.
四、解答题
12.【答案】 (1)
缩小前后的长方形面积比是4:1。
(2)
(3)圆锥;3.14×32×2×=18.84(cm3)
【解析】【分析】(1)缩小前长方形的面积为:4×2=8,缩小后长方形的面积为:2×1=2,缩小前后长方形面积比是:8:2=4:1。
(2)用数对表示物体的位置,先列后行。图形旋转时,旋转中心不变,注意旋转方向,90°是与原来的边垂直。
(3)以直角三角形的一条直角边旋转一周,形成圆锥,圆锥的底面半径是3厘米,高是2厘米,代入圆锥的体积计算公式:V=πr2h,即可计算圆锥的体积。
13.【答案】解:圆柱是由两个相同的圆形底面和一个侧面组成的,侧面展开后是一个长方形;圆锥是由一个底面和一个侧面组成的,底面是圆形,侧面展开后是一个扇形.圆柱有无数条高,圆锥只有一条高.
【解析】【分析】根据圆柱和圆锥的底面、侧面以及高的条数区别圆柱和圆锥的特征即可.
五、应用题
14.【答案】 解:浸在水中的圆锥体体积为14×14×(12﹣8)=784(立方厘米),
露出水面部分的小圆锥的高为12厘米,其高是大圆锥的 ,半径也是大圆锥的 ,所以体积是大圆锥的 = ,即露出水面的小圆锥体与整个圆锥体的体积之比为1:8,
所以整个圆锥体体积为784÷(1﹣ )=896(立方厘米),
圆锥体底面积为896÷( ×24)=112(平方厘米).
答:圆锥的底面积是112立方厘米.
【解析】【分析】由题意得:浸在水中的部分的体积等于高为12﹣8=4厘米的长方体的体积,即:14×14×(12﹣8)=784立方厘米;露出水面部分的小圆锥的高为12厘米,其高是大圆锥的 ,半径也是大圆锥的 ,所以体积是大圆锥的 = ,所以露出水面的小圆锥体与整个圆锥体的体积之比为1:8,所以浸在水中的部分圆锥体的体积是整个圆锥体体积的1﹣ ,用除法即可求出大圆锥体的体积,进而即可求出底面积.解答此题的关键是先求出浸入水中的部分占圆锥体积的几分之几,从而问题得解.
一、单选题
1.一个圆锥的体积是18立方分米,比与它等底等高的圆柱的体积少(??? )立方分米。
A.?36?????????????????????????????????????????B.?24?????????????????????????????????????????C.?9?????????????????????????????????????????D.?18?
2.把一个圆柱铸成一个圆锥体,它的(??? )不变。
A.?体积???????????????????????????????????????B.?表面积???????????????????????????????????????C.?侧面积
3.把一支新的圆柱形铅笔削尖,笔尖(圆锥部分)的体积是削去部分的( ??)。
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?2倍
4.一个圆锥的体积是30立方米,和它等底等高的圆柱的体积是(???? )立方米。
A.?30????????????????????????????????????????????B.?10????????????????????????????????????????????C.?90
二、判断题
5.一个圆锥的体积是6立方厘米,那么圆柱的体积是18立方厘米.(? )
6.一个圆锥体的高扩大2倍,底面积缩小2倍,它的体积不变。( )
7.若圆锥的体积是圆柱的 ,那么它们一定是等底等高。(?? )
8.一个圆柱的体积是一个圆锥体积的3倍,那么它们一定等底等高.( ??)
三、填空题
9.一个底面半径4分米,高6分米的圆锥体沙堆,它的体积是________立方分米.
10.一个高45cm的圆锥体容器,盛满水后再倒入和它等底等高的圆柱体容器里,水面的高度是________cm.
11.计算圆锥的体积________.(图中单位:厘米)
四、解答题
12.想一想,画一画。
(1)把长方形①按2:1的比例进行缩小,画出新图形。缩小前后的长方形面积比是________。
(2)请标出A(1,1)、B(3,1)、C(3,4)三个点,用线连起来,组成一个△ABC,再绕B点顺时针旋转90°,请画出旋转后的图形△B'C'A'。
(3)如果将△B'C'A'以B'A'为轴旋转一周,会形成________图形,在横线上列式求出该图形的体积?(每格是边长1厘米的正方形)
________
13.想一想,和你的同桌说一说圆柱和圆锥各有什么特点,并记录下来.
五、应用题
14.一个底面是正方形的容器里装着水,从里面量边长是14厘米,水面高度是8厘米,把一个铁质实心圆锥直立(底面与容器底部接触)在容器以后,水的高度上升到12厘米,正好是圆锥高的 ,求圆锥的底面积是多少?
参考答案
一、单选题
1.【答案】A
【解析】【解答】18×3-18
=54-18
=36(立方分米)
故答案为:A.
【分析】等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍,已知圆锥的体积,用圆锥的体积×3=圆柱的体积,然后用减法求出圆锥比圆柱体积少的部分,据此列式解答.
2.【答案】 A
【解析】【解答】 把一个圆柱铸成一个圆锥体,它的体积不变。
故答案为:A。
【分析】此题主要考查了体积的认识,在物体熔铸的过程中,形状会发生变化,体积不变。
3.【答案】 B
【解析】【解答】3–1=2;1÷2=
故答案为:B
【分析】题意可知,把一个圆柱削成一个等底等高的圆锥,圆锥的体积等于和它等底等高圆柱体积的三分之一,即把圆柱体积看作单位“1”平均分成3份,圆锥体积占1份,削去部分占2份, 笔尖(圆锥部分)的体积是削去部分的 。
4.【答案】 C
【解析】【解答】30×3=90(立方米)
答:圆柱的体积是90立方米。
故选:C
【分析】等底等高的圆柱的体积是圆锥体积的3倍,圆锥的体积已知,求圆柱的体积,可用圆锥的体积乘3进行计算即可得到答案。
二、判断题
5.【答案】 错误
【解析】【解答】圆锥和圆柱的底面积和高都不知道,所以它们的体积没有关系,原题说法错误。
故答案为:错误。
【分析】等底等高的圆柱的体积是圆锥体积的3倍,据此解答。
6.【答案】正确
【解析】解答:
分析:由圆锥的体积公式可得。
7.【答案】 错误
【解析】【解答】解:若圆锥的体积是圆柱的, 那么它们不一定等底等高。原题说法错误。
故答案为:错误。
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×, 等底等高的圆锥体积是圆柱的;但是圆锥的体积是圆柱的, 它们不一定等底等高。
8.【答案】 错误
【解析】【解答】因为等底等高的圆柱体的体积是圆锥体体积的3倍,所以如果圆柱体积是圆锥体积的3倍,那么它们的底和高度的乘积是相等的,但是底和高不一定相等,原题说法错误。
故答案为:错误。
【分析】此题主要考查了圆柱和圆锥的体积关系,等底等高的圆柱体的体积是圆锥体体积的3倍,如果圆柱体积是圆锥体积的3倍,那么它们的底和高的乘积是相等的,但是底和高不一定相等,据此判断。
三、填空题
9.【答案】 100.48
【解析】【解答】解:
=
=100.48(立方分米)
答:它的体积是100.48立方分米.
10.【答案】 15
【解析】【解答】45×=15(cm)。
所以倒入圆柱容器中,水面的高度为15cm。
故答案为:15。
【分析】圆柱的体积=底面积×高,圆锥的体积=×底面积×高,本题中水的体积一定即圆柱的体积=圆锥的体积,圆柱与圆锥等底即圆柱与圆锥的底面积相等,即可得出圆柱的高=×圆锥的高。
11.【答案】 75.36立方厘米
【解析】【解答】8÷2=4(厘米)
×3.14×42×4.5
=×3.14×16×4.5
=3.14×16×1.5
=50.24×1.5
=75.36(立方厘米)
故答案为:75.36
【分析】已知圆锥的底面直径和高,求圆锥的体积,先求出圆锥的底面半径,然后用公式:V=πr2h,据此列式解答.
四、解答题
12.【答案】 (1)
缩小前后的长方形面积比是4:1。
(2)
(3)圆锥;3.14×32×2×=18.84(cm3)
【解析】【分析】(1)缩小前长方形的面积为:4×2=8,缩小后长方形的面积为:2×1=2,缩小前后长方形面积比是:8:2=4:1。
(2)用数对表示物体的位置,先列后行。图形旋转时,旋转中心不变,注意旋转方向,90°是与原来的边垂直。
(3)以直角三角形的一条直角边旋转一周,形成圆锥,圆锥的底面半径是3厘米,高是2厘米,代入圆锥的体积计算公式:V=πr2h,即可计算圆锥的体积。
13.【答案】解:圆柱是由两个相同的圆形底面和一个侧面组成的,侧面展开后是一个长方形;圆锥是由一个底面和一个侧面组成的,底面是圆形,侧面展开后是一个扇形.圆柱有无数条高,圆锥只有一条高.
【解析】【分析】根据圆柱和圆锥的底面、侧面以及高的条数区别圆柱和圆锥的特征即可.
五、应用题
14.【答案】 解:浸在水中的圆锥体体积为14×14×(12﹣8)=784(立方厘米),
露出水面部分的小圆锥的高为12厘米,其高是大圆锥的 ,半径也是大圆锥的 ,所以体积是大圆锥的 = ,即露出水面的小圆锥体与整个圆锥体的体积之比为1:8,
所以整个圆锥体体积为784÷(1﹣ )=896(立方厘米),
圆锥体底面积为896÷( ×24)=112(平方厘米).
答:圆锥的底面积是112立方厘米.
【解析】【分析】由题意得:浸在水中的部分的体积等于高为12﹣8=4厘米的长方体的体积,即:14×14×(12﹣8)=784立方厘米;露出水面部分的小圆锥的高为12厘米,其高是大圆锥的 ,半径也是大圆锥的 ,所以体积是大圆锥的 = ,所以露出水面的小圆锥体与整个圆锥体的体积之比为1:8,所以浸在水中的部分圆锥体的体积是整个圆锥体体积的1﹣ ,用除法即可求出大圆锥体的体积,进而即可求出底面积.解答此题的关键是先求出浸入水中的部分占圆锥体积的几分之几,从而问题得解.
