北师大版五年级下册数学2.2展开与折叠(含解析)
文档属性
| 名称 | 北师大版五年级下册数学2.2展开与折叠(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 231.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 16:28:17 | ||
图片预览

文档简介
2.2展开与折叠
一、单选题
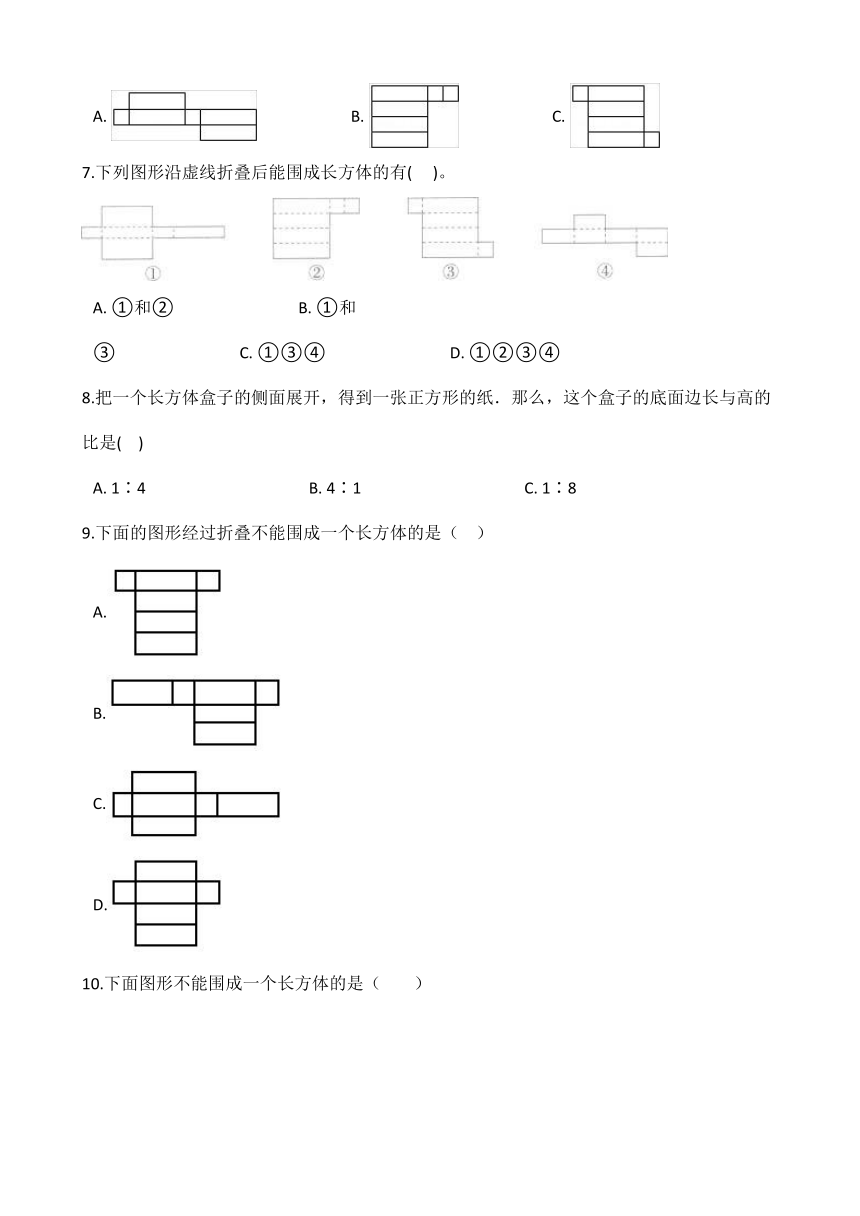
1.下列四个平面图形中,不能折叠成无盖的长方体盒子的是( )
A.????????B.????????C.????????D.?
2.下面的四个图形不能折叠成三棱柱的是( )
A.????????????????B.????????????????C.????????????????D.?
3.如图最有可能是( )的展开图.
A.??????????????????????????B.??????????????????????????C.??????????????????????????D.?
4.左图最有可能是( )的展开示意图.
A.??????????????????B.??????????????????C.??????????????????D.?
5.把下面两幅图分别折成正方体(每个小方格大小一致),它们体积的比是( )
A.?2:1?????????????????????????????????????????B.?4:1?????????????????????????????????????????C.?8:1
6.在如图图形中,( )不是长方体的展开图.
A.????????????????????????B.????????????????????????C.?
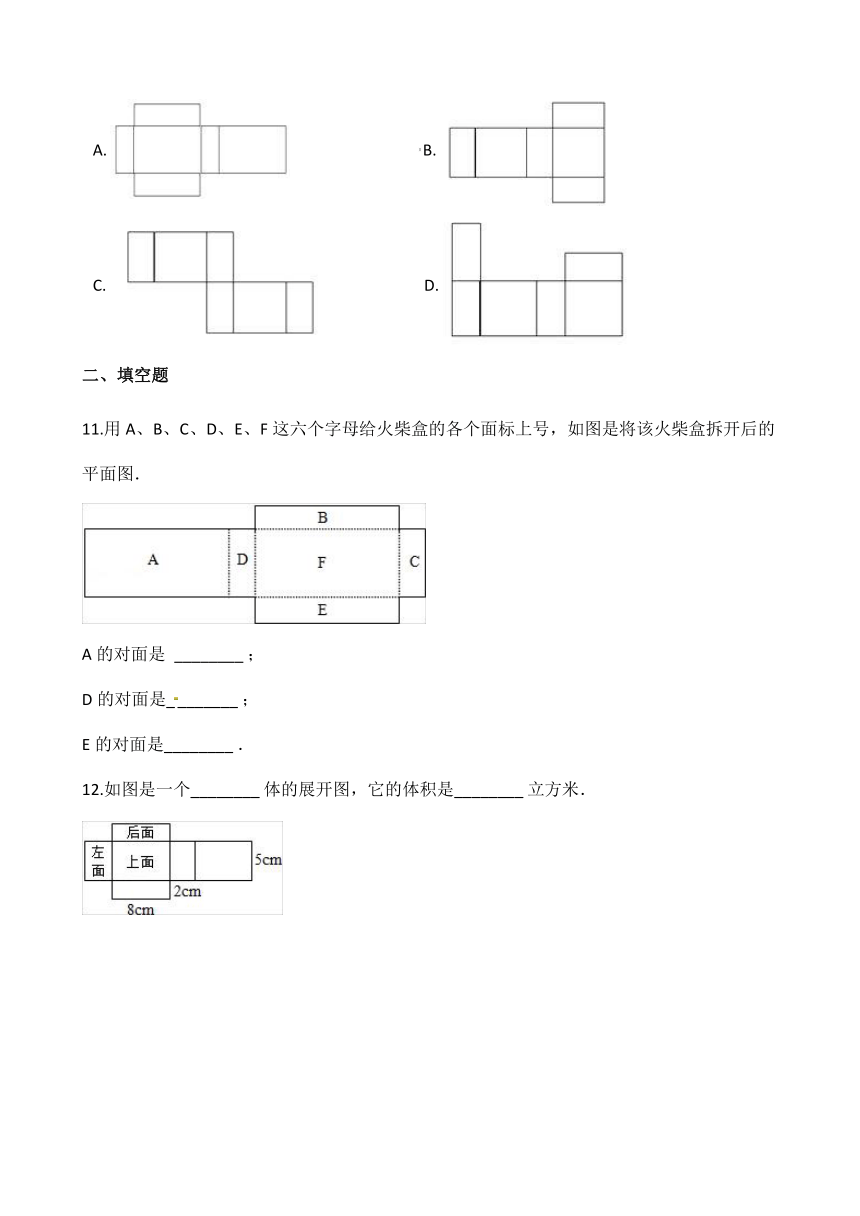
7.下列图形沿虚线折叠后能围成长方体的有(???
)。
A.?①和②???????????????????????????????B.?①和③???????????????????????????????C.?①③④???????????????????????????????D.?①②③④
8.把一个长方体盒子的侧面展开,得到一张正方形的纸.那么,这个盒子的底面边长与高的比是(??
)
A.?1∶4?????????????????????????????????????????B.?4∶1?????????????????????????????????????????C.?1∶8
9.下面的图形经过折叠不能围成一个长方体的是(??
)
A.
B.
C.
D.
10.下面图形不能围成一个长方体的是(??????
)
A.??????????????????????????????????B.?
C.????????????????????????????D.?
二、填空题
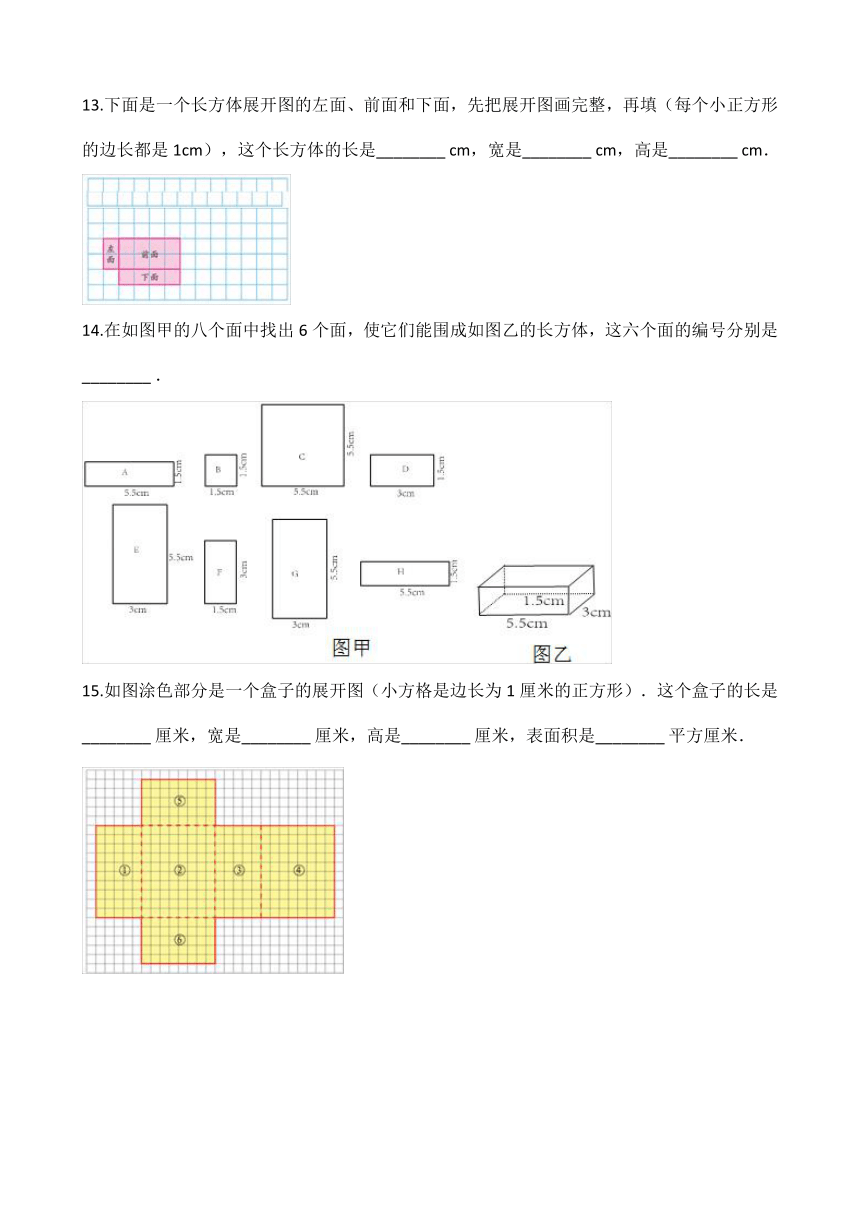
11.用A、B、C、D、E、F这六个字母给火柴盒的各个面标上号,如图是将该火柴盒拆开后的平面图.
A的对面是
________?;
D的对面是________?;
E的对面是________?.
12.如图是一个________?体的展开图,它的体积是________?立方米.
13.下面是一个长方体展开图的左面、前面和下面,先把展开图画完整,再填(每个小正方形的边长都是1cm),这个长方体的长是________?cm,宽是________?cm,高是________?cm.
14.在如图甲的八个面中找出6个面,使它们能围成如图乙的长方体,这六个面的编号分别是________?.
15.如图涂色部分是一个盒子的展开图(小方格是边长为1厘米的正方形).这个盒子的长是________?厘米,宽是________?厘米,高是________?厘米,表面积是________?平方厘米.
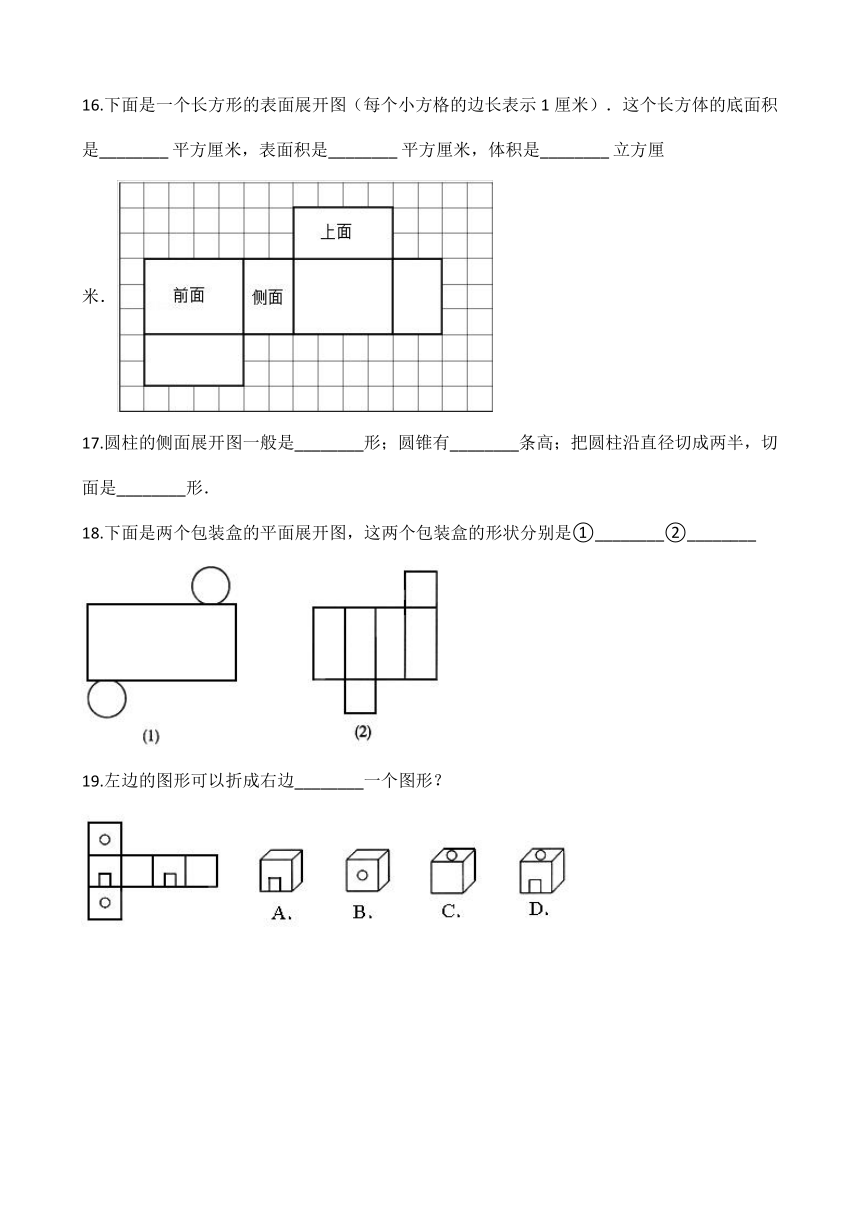
16.下面是一个长方形的表面展开图(每个小方格的边长表示1厘米).这个长方体的底面积是________?平方厘米,表面积是________?平方厘米,体积是________?立方厘米.
17.圆柱的侧面展开图一般是________形;圆锥有________条高;把圆柱沿直径切成两半,切面是________形.
18.下面是两个包装盒的平面展开图,这两个包装盒的形状分别是①________②________
19.左边的图形可以折成右边________一个图形?
20.动动手,折折看,下面________几幅图形可以折成圆圈中的图形。
三、应用题
21.请你把各图形的展开图用线连一连.
22.右面是一个纸盒的展开图(无盖).
(1)做这个纸盒需要多大的纸板?
(2)这个纸盒的容积是多少?(纸板厚度忽略不计)
23.底面是正方形的长方体包装盒高20cm,侧面展开后是一个正方形,这个长方体的体积是多少立方厘米?
24.这是长方体的展开图,求出它的表面积和体积.
25.在展开图上找出相对的面,并用上、下、左、右标出,再用a、b、h标出三条边.
答案解析部分
一、单选题
1.【答案】C
【解答】解:下列四个平面图形中,不能折叠成无盖的长方体盒子的是图C;
故选:C
【分析】根据长方体展开图的
特征,图A、图B和图D都属于“1
4
1”结构,且对折后相对的面相同,都能折叠成无盖的长方体盒子;图C虽然也属于“1
4
1”结构,少一个侧面,一个侧面重复,不能折叠无盖的长方体盒子.本题主要是考查长方体展开图的特征,长方体与正方体展开图的特征类似,都有11种情况,
不同的是长方体的展开图还要看相对的面是否相同.
2.【答案】D
【解答】解:A,折叠后可得到三棱柱;
B,折叠后可得到三棱柱;
C,折叠后可得到三棱柱;
D,折叠后两个底面重合,不能得到三棱柱;
故选:D.
【分析】根据三棱柱的特征,它的上、下两个底面是完全相同的三角形,三个侧面是完全相同的长方形,再根据三棱柱表面展开图的特点进行解答即可.
3.【答案】C
【解答】解:由分析得出:如图最有可能是C图的展开图.
故选:C.
【分析】根据展开图得出:侧面是四个一样大小的长方形,上下2个底面是正方形,据此判断即可.解决本题的关键是根据展开图的特征找出符合的图形.
4.【答案】D
【解答】解:由分析得出:如图最有可能是D图的展开图.
故选:D.
【分析】根据展开图得出:侧面是四个一样大小的长方形,上下2个底面是正方形,据此判断即可.解决本题的关键是根据展开图的特征找出符合的图形.
5.【答案】C
【解答】解:图1体积:2×2×2=8,
图2体积:1×1×1=1,
它们体积的比是8:1.
故选:C.
【分
析】根据题意,设每个小方格的边长为1,那么图一被折成的正方体的长、宽、高都是2,图二被折成的正方体的长、宽、高都是1;由正方体体积公式计算出正方
体的体积,相比即可.此题考查了正方体空间图形的体积,关键在于设每个小方格的边长为1,求出每个折成的正方体的体积,进而解决问题.
6.【答案】B
【解答】解:根据长方体展开图的特征,图A和图C是长方体展开图,而图B不能折叠成长方体,不是长方体展开图.
故选:B.
【分
析】长方体展开图与正方体展开图类似,不同的是正方体展开图的六个面都是相同的正方形,长方体展开图只有对面是相同的长方形(特殊情况有相对的两个面是相
同的正方形).图A及图C的四个长方形组成长方体的侧面,两个正方形组成长方体的上、下底,是长方体展开图,都属于“1﹣4﹣1”型,图B的四个长方形组
成长方体的侧面,两个正方形在同一侧,不能折叠成长方体,不是长方体展开图.
7.【答案】B
【解答】①、③都符合长方体的展开图的特点,所以都可以折叠成长方体;②的宽都在同一侧了,所以不能折成长方体;
故答案为:A。
【分析】本题考点:长方体的展开图.
此题主要考查了展开图折叠成几何体,考查同学们的空间想象能力.
由平面图形的折叠及立体图形的表面展开图的特点解题.
8.【答案】A
【解答】把一个长方体盒子的侧面展开,得到一张正方形的纸.那么,这个盒子的底面边长与高的比是1:4.
故答案为:A.
【分析】把一个长方体盒子的侧面展开,得到一张正方形的纸.因为正方形的边长相等,所以这个盒子的高是盒子底面边长的4倍,据此解答.
9.【答案】B
【解答】解:B选项中折叠后会有重叠的面,不能围成一个长方体.
故答案为:B
【分析】以一个面为底面,分别判断出每个选项中的展开图中有没有重叠的面,如果有重叠的面就不能组成长方体,没有重叠的面就能围成长方体.
10.【答案】D
【解析】【解答】根据分析可知,
选项A、B属于一四一型,是长方体的展开图;
选项C属于三三型,是长方体的展开图;
选项D不是长方体展开图的类型.
故答案为:D.【分析】观察长方体展开图,可以发现:①展开图都是由3对长方形组成的,每对长方形的大小完全相同;②长方体长、宽、高均不相等,那么其展开图,在同一行或同一列中,如有3个或4个长方形的其中完全相同的两个长方形中间一定只隔一个其他的长方形,如果是两个长方形相连,那么这两个长方形一定不完全相同,(有两个相对的面是正方形的长方体的表面展开图例外);③长、宽、高均不相等的长方体的表面展开图:一四一式27种;二三一式18种;二二二式6种;三三式3种,共计54种,据此解答.
二、填空题
11.【答案】F;C;B
【解答】解:由分析可知:
A的对面是F;
D的对面是C;
E的对面是B;
故答案为:F,C,B.
【分析】根据长方体的特征:6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的形状相同,依此根据长方体的展开图的形状解答即可.
12.【答案】长方体;0.0002
【解答】解:如图,
把它折成的长方体的长、宽、高分别是8cm、5cm、5cm的长方体,
8×5×5
=200(cm3)
=0.0002立方米;
故答案为:长方体,0.0002.
【分析】如图是一个长方体展开图,把它折成的长方体的长、宽、高分别是8cm、5cm、5cm的长方体,根据长方体的体积公式V=abh即可求出这个长方体的体积.
13.【答案】4;2;1
【解析】【解答】解(1)根据分析,画图如下:
(2)这个长方体的长是4cm,宽是2cm,高是1cm.
故答案为;4,2,1.
【分
析】(1)根据长方体展开图的特征,可以把它补成“141”结构,即在它的前面图的右面画出它的右面图,再在右面图的右面在它的上面画出它的后面,在前面
图的上面画出它的上面图,长方体展开图对面相同.(2)把这张长方体的展开图折成长方体后,长、宽、高分别是4厘米、2厘米、1厘米.
14.【答案】E、G、A、H、D、F
【解析】【解答】解:由图乙可知:这个长方体的长是5.5厘米、宽是3厘米、高是1.5厘米,
所以选择E、G作为长方体的上下面,A、H作为长方体的前后面,D、F在为长方体的左右面,
故答案为:E、G、A、H、D、F.
【分析】根据长方体的特征:长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相等.据此解答.此题考查的目的是理解掌握长方体的特征.
15.【答案】10;8;5;340
【解析】【解答】解:观察图形可知,这个盒子的长是
10厘米,宽是
8厘米,高是
5厘米,
(10×8+10×5+8×5)×2
=(80+50+40)×2
=170×2
=340(平方厘米)
答:这个盒子的长是
10厘米,宽是
8厘米,高是
5厘米,表面积是
340平方厘米.
故答案为:10,8,5,340.
【分析】根据图可知:长方体盒子的长为10厘米,宽为8厘米,高为5厘米,根据长方体的表面积公式:s=(ab+ah+bh)×2,解答即可.此题考查的目的是理解掌握长方体的展开图的特征,以及长方体的表面积公式的灵活运用.
16.【答案】8;52;24
【解析】【解答】解:通过图知道这个长方体的长是4厘米,宽是2厘米,高是3厘米,
底面积:4×2=8(平方厘米),
表面积:(4×2+4×3+2×3)×2
=26×2
=52(平方厘米);
体积:4×2×3=24(立方厘米);
答:这个长方体的底面积是8平方厘米,表面积是52平方厘米,体积是24立方厘米;
故答案为:8,52,24.
【分析】通过图知道这个长方体的长是4厘米,宽是2厘米,高是3厘米,由此根据:长方体的底面积=长×宽,求出长方体的底面积,根据:长方体的表面积=(长×宽+长×高+宽×高)×2,求出长方体的表面积,根据:长方体的体积=长×宽×高,即可求出它的体积.
17.【答案】长方;一;长方
【解析】【解答】解:圆柱的侧面展开图一般是长方形;圆锥有一条高;把圆柱沿直径切成两半,切面是长方形.
故答案为:长方,一,长方.
【分析】把圆柱沿高展开,会得到一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,如果圆柱的底面周长等于圆柱的高,即长方形的长等于宽,那么此展开图就是正方形;把圆柱沿直径切成两半,切面是长方形;根据圆锥的特征得出圆锥有一条高,据此解答.
18.【答案】圆柱体;长方体
【解析】【解答】观察图1的平面展开图可知,这个立体图形是由一个长方形侧面和两个圆形底面组成的,据此可以得到这个包装盒是圆柱体;
观察图2的平面展开图可知,这个立体图形是由6个长方形组成,据此可以得到这个包装盒是长方体.
故答案为:圆柱体;长方体.
【分析】根据常见立体图形圆柱体、长方体、正方体的平面展开图的特征判断即可.
19.【答案】D
【解析】【解答】观察四个图形,可以看到第四个图形中圆与正方形相邻,而另外三个图形它们不相邻。
故选:D
【分析】解答此题要根据展开图中圆与正方形相邻的特点,具备这个特点只有第四个图形。
20.【答案】A,E,F
【解析】【解答】解:正方体展开后有6个正方形的面,因此A是正方体的展开图;第二个物体展开后是4个三角形,因此E是它的展开图,长方体展开后有6个面,因此F是长方体的展开图.
故答案为:A,E,F
【分析】观察着几个物体展开后有几个面,根据面的个数及面的形状判断哪些图形可以折成圆圈中的图形即可.
三、应用题
21.【答案】解:连线如下:
【解析】【分析】结合圆柱、长方体、圆锥展开图的特点进行连线.注意圆柱是上下两个圆形的底面和一个长方形侧面组成,长方体是六个长方形组成,圆锥是一个扇形和一个底面圆组成.考查了立体图形的展开图,熟记常见立体图形的平面展开图的特征是解决此类问题的关键.
22.【答案】解:长方体的长是30厘米,宽是30厘米,高是12厘米,
表面积为:
30×12×4+30×30
=1440+900
=2340(平方厘米)
体积为:30×30×12=10800(立方厘米).
答:做这个纸盒需要2340平方厘米的纸板;这个纸盒的容积是10800立方厘米.
【解析】【分析】由展开图得出长方体的长是30厘米,宽是30厘米,高是12厘米;再根据长方体表面积和体积的公式计算即可.解决本题的关键是根据展开图找出长方体的长、宽、高,再根据表面积公式和体积公式计算即可.
23.【答案】解:20÷4=5(厘米),
5×5×20
=25×20
=500(立方厘米),
答:这个长方体的体积是500立方厘米.
【解析】【分析】根据题意可知:这个长方体的底面周长和高相等,首先用底面周长除以4求出底面边长,再根据长方体的体积公式解答即可.此题主要考查长方体的体积公式的灵活运用.
24.【答案】解:(1)(20﹣8)÷2=6(厘米)
(10×8+10×6+8×6)×2
=(80+60+48)×2
=188×2
=376(平方厘米)
答:表面积是376平方厘米.
(2)10×8×6=480(立方厘米)
答:体积是480立方厘米.
【解析】【分析】由展开图得出长方体的长是10厘米,宽是8厘米,高是(20﹣8)÷2=6(厘米),再根据长方体表面积=长×宽×2+长×高×2+宽×高×2;长方体体积=长×宽×高,计算即可.解决本题的关键是根据展开图找出长方体的长、宽、高,再根据表面积公式和体积公式计算即可.
25.【答案】解:在展开图上找出相对的面,并用上、下、左、右标出,再用a,b,c标出每条棱(下图)
【解析】【分析】根据长方体展开图的特征,右图属于左图的展开图,展开后相同颜色的面为相对的面,根据相对面的长、宽分别相等,由左图所标出的各棱,即可在右图中分别并用上、下、左、右标出,再用a,b,c标出每条棱.此题是考查长方体展开图的特征,长方体展开图与正方体展开图类似,但要复杂,正方体展开图的六相面是相等的正方形,长方体展开图对面是相同的长方形形(特殊长方体有一组对面是正方形,其余是四个相同的长方形).
一、单选题
1.下列四个平面图形中,不能折叠成无盖的长方体盒子的是( )
A.????????B.????????C.????????D.?
2.下面的四个图形不能折叠成三棱柱的是( )
A.????????????????B.????????????????C.????????????????D.?
3.如图最有可能是( )的展开图.
A.??????????????????????????B.??????????????????????????C.??????????????????????????D.?
4.左图最有可能是( )的展开示意图.
A.??????????????????B.??????????????????C.??????????????????D.?
5.把下面两幅图分别折成正方体(每个小方格大小一致),它们体积的比是( )
A.?2:1?????????????????????????????????????????B.?4:1?????????????????????????????????????????C.?8:1
6.在如图图形中,( )不是长方体的展开图.
A.????????????????????????B.????????????????????????C.?
7.下列图形沿虚线折叠后能围成长方体的有(???
)。
A.?①和②???????????????????????????????B.?①和③???????????????????????????????C.?①③④???????????????????????????????D.?①②③④
8.把一个长方体盒子的侧面展开,得到一张正方形的纸.那么,这个盒子的底面边长与高的比是(??
)
A.?1∶4?????????????????????????????????????????B.?4∶1?????????????????????????????????????????C.?1∶8
9.下面的图形经过折叠不能围成一个长方体的是(??
)
A.
B.
C.
D.
10.下面图形不能围成一个长方体的是(??????
)
A.??????????????????????????????????B.?
C.????????????????????????????D.?
二、填空题
11.用A、B、C、D、E、F这六个字母给火柴盒的各个面标上号,如图是将该火柴盒拆开后的平面图.
A的对面是
________?;
D的对面是________?;
E的对面是________?.
12.如图是一个________?体的展开图,它的体积是________?立方米.
13.下面是一个长方体展开图的左面、前面和下面,先把展开图画完整,再填(每个小正方形的边长都是1cm),这个长方体的长是________?cm,宽是________?cm,高是________?cm.
14.在如图甲的八个面中找出6个面,使它们能围成如图乙的长方体,这六个面的编号分别是________?.
15.如图涂色部分是一个盒子的展开图(小方格是边长为1厘米的正方形).这个盒子的长是________?厘米,宽是________?厘米,高是________?厘米,表面积是________?平方厘米.
16.下面是一个长方形的表面展开图(每个小方格的边长表示1厘米).这个长方体的底面积是________?平方厘米,表面积是________?平方厘米,体积是________?立方厘米.
17.圆柱的侧面展开图一般是________形;圆锥有________条高;把圆柱沿直径切成两半,切面是________形.
18.下面是两个包装盒的平面展开图,这两个包装盒的形状分别是①________②________
19.左边的图形可以折成右边________一个图形?
20.动动手,折折看,下面________几幅图形可以折成圆圈中的图形。
三、应用题
21.请你把各图形的展开图用线连一连.
22.右面是一个纸盒的展开图(无盖).
(1)做这个纸盒需要多大的纸板?
(2)这个纸盒的容积是多少?(纸板厚度忽略不计)
23.底面是正方形的长方体包装盒高20cm,侧面展开后是一个正方形,这个长方体的体积是多少立方厘米?
24.这是长方体的展开图,求出它的表面积和体积.
25.在展开图上找出相对的面,并用上、下、左、右标出,再用a、b、h标出三条边.
答案解析部分
一、单选题
1.【答案】C
【解答】解:下列四个平面图形中,不能折叠成无盖的长方体盒子的是图C;
故选:C
【分析】根据长方体展开图的
特征,图A、图B和图D都属于“1
4
1”结构,且对折后相对的面相同,都能折叠成无盖的长方体盒子;图C虽然也属于“1
4
1”结构,少一个侧面,一个侧面重复,不能折叠无盖的长方体盒子.本题主要是考查长方体展开图的特征,长方体与正方体展开图的特征类似,都有11种情况,
不同的是长方体的展开图还要看相对的面是否相同.
2.【答案】D
【解答】解:A,折叠后可得到三棱柱;
B,折叠后可得到三棱柱;
C,折叠后可得到三棱柱;
D,折叠后两个底面重合,不能得到三棱柱;
故选:D.
【分析】根据三棱柱的特征,它的上、下两个底面是完全相同的三角形,三个侧面是完全相同的长方形,再根据三棱柱表面展开图的特点进行解答即可.
3.【答案】C
【解答】解:由分析得出:如图最有可能是C图的展开图.
故选:C.
【分析】根据展开图得出:侧面是四个一样大小的长方形,上下2个底面是正方形,据此判断即可.解决本题的关键是根据展开图的特征找出符合的图形.
4.【答案】D
【解答】解:由分析得出:如图最有可能是D图的展开图.
故选:D.
【分析】根据展开图得出:侧面是四个一样大小的长方形,上下2个底面是正方形,据此判断即可.解决本题的关键是根据展开图的特征找出符合的图形.
5.【答案】C
【解答】解:图1体积:2×2×2=8,
图2体积:1×1×1=1,
它们体积的比是8:1.
故选:C.
【分
析】根据题意,设每个小方格的边长为1,那么图一被折成的正方体的长、宽、高都是2,图二被折成的正方体的长、宽、高都是1;由正方体体积公式计算出正方
体的体积,相比即可.此题考查了正方体空间图形的体积,关键在于设每个小方格的边长为1,求出每个折成的正方体的体积,进而解决问题.
6.【答案】B
【解答】解:根据长方体展开图的特征,图A和图C是长方体展开图,而图B不能折叠成长方体,不是长方体展开图.
故选:B.
【分
析】长方体展开图与正方体展开图类似,不同的是正方体展开图的六个面都是相同的正方形,长方体展开图只有对面是相同的长方形(特殊情况有相对的两个面是相
同的正方形).图A及图C的四个长方形组成长方体的侧面,两个正方形组成长方体的上、下底,是长方体展开图,都属于“1﹣4﹣1”型,图B的四个长方形组
成长方体的侧面,两个正方形在同一侧,不能折叠成长方体,不是长方体展开图.
7.【答案】B
【解答】①、③都符合长方体的展开图的特点,所以都可以折叠成长方体;②的宽都在同一侧了,所以不能折成长方体;
故答案为:A。
【分析】本题考点:长方体的展开图.
此题主要考查了展开图折叠成几何体,考查同学们的空间想象能力.
由平面图形的折叠及立体图形的表面展开图的特点解题.
8.【答案】A
【解答】把一个长方体盒子的侧面展开,得到一张正方形的纸.那么,这个盒子的底面边长与高的比是1:4.
故答案为:A.
【分析】把一个长方体盒子的侧面展开,得到一张正方形的纸.因为正方形的边长相等,所以这个盒子的高是盒子底面边长的4倍,据此解答.
9.【答案】B
【解答】解:B选项中折叠后会有重叠的面,不能围成一个长方体.
故答案为:B
【分析】以一个面为底面,分别判断出每个选项中的展开图中有没有重叠的面,如果有重叠的面就不能组成长方体,没有重叠的面就能围成长方体.
10.【答案】D
【解析】【解答】根据分析可知,
选项A、B属于一四一型,是长方体的展开图;
选项C属于三三型,是长方体的展开图;
选项D不是长方体展开图的类型.
故答案为:D.【分析】观察长方体展开图,可以发现:①展开图都是由3对长方形组成的,每对长方形的大小完全相同;②长方体长、宽、高均不相等,那么其展开图,在同一行或同一列中,如有3个或4个长方形的其中完全相同的两个长方形中间一定只隔一个其他的长方形,如果是两个长方形相连,那么这两个长方形一定不完全相同,(有两个相对的面是正方形的长方体的表面展开图例外);③长、宽、高均不相等的长方体的表面展开图:一四一式27种;二三一式18种;二二二式6种;三三式3种,共计54种,据此解答.
二、填空题
11.【答案】F;C;B
【解答】解:由分析可知:
A的对面是F;
D的对面是C;
E的对面是B;
故答案为:F,C,B.
【分析】根据长方体的特征:6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面的形状相同,依此根据长方体的展开图的形状解答即可.
12.【答案】长方体;0.0002
【解答】解:如图,
把它折成的长方体的长、宽、高分别是8cm、5cm、5cm的长方体,
8×5×5
=200(cm3)
=0.0002立方米;
故答案为:长方体,0.0002.
【分析】如图是一个长方体展开图,把它折成的长方体的长、宽、高分别是8cm、5cm、5cm的长方体,根据长方体的体积公式V=abh即可求出这个长方体的体积.
13.【答案】4;2;1
【解析】【解答】解(1)根据分析,画图如下:
(2)这个长方体的长是4cm,宽是2cm,高是1cm.
故答案为;4,2,1.
【分
析】(1)根据长方体展开图的特征,可以把它补成“141”结构,即在它的前面图的右面画出它的右面图,再在右面图的右面在它的上面画出它的后面,在前面
图的上面画出它的上面图,长方体展开图对面相同.(2)把这张长方体的展开图折成长方体后,长、宽、高分别是4厘米、2厘米、1厘米.
14.【答案】E、G、A、H、D、F
【解析】【解答】解:由图乙可知:这个长方体的长是5.5厘米、宽是3厘米、高是1.5厘米,
所以选择E、G作为长方体的上下面,A、H作为长方体的前后面,D、F在为长方体的左右面,
故答案为:E、G、A、H、D、F.
【分析】根据长方体的特征:长方体的6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相等.据此解答.此题考查的目的是理解掌握长方体的特征.
15.【答案】10;8;5;340
【解析】【解答】解:观察图形可知,这个盒子的长是
10厘米,宽是
8厘米,高是
5厘米,
(10×8+10×5+8×5)×2
=(80+50+40)×2
=170×2
=340(平方厘米)
答:这个盒子的长是
10厘米,宽是
8厘米,高是
5厘米,表面积是
340平方厘米.
故答案为:10,8,5,340.
【分析】根据图可知:长方体盒子的长为10厘米,宽为8厘米,高为5厘米,根据长方体的表面积公式:s=(ab+ah+bh)×2,解答即可.此题考查的目的是理解掌握长方体的展开图的特征,以及长方体的表面积公式的灵活运用.
16.【答案】8;52;24
【解析】【解答】解:通过图知道这个长方体的长是4厘米,宽是2厘米,高是3厘米,
底面积:4×2=8(平方厘米),
表面积:(4×2+4×3+2×3)×2
=26×2
=52(平方厘米);
体积:4×2×3=24(立方厘米);
答:这个长方体的底面积是8平方厘米,表面积是52平方厘米,体积是24立方厘米;
故答案为:8,52,24.
【分析】通过图知道这个长方体的长是4厘米,宽是2厘米,高是3厘米,由此根据:长方体的底面积=长×宽,求出长方体的底面积,根据:长方体的表面积=(长×宽+长×高+宽×高)×2,求出长方体的表面积,根据:长方体的体积=长×宽×高,即可求出它的体积.
17.【答案】长方;一;长方
【解析】【解答】解:圆柱的侧面展开图一般是长方形;圆锥有一条高;把圆柱沿直径切成两半,切面是长方形.
故答案为:长方,一,长方.
【分析】把圆柱沿高展开,会得到一个长方形,这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,如果圆柱的底面周长等于圆柱的高,即长方形的长等于宽,那么此展开图就是正方形;把圆柱沿直径切成两半,切面是长方形;根据圆锥的特征得出圆锥有一条高,据此解答.
18.【答案】圆柱体;长方体
【解析】【解答】观察图1的平面展开图可知,这个立体图形是由一个长方形侧面和两个圆形底面组成的,据此可以得到这个包装盒是圆柱体;
观察图2的平面展开图可知,这个立体图形是由6个长方形组成,据此可以得到这个包装盒是长方体.
故答案为:圆柱体;长方体.
【分析】根据常见立体图形圆柱体、长方体、正方体的平面展开图的特征判断即可.
19.【答案】D
【解析】【解答】观察四个图形,可以看到第四个图形中圆与正方形相邻,而另外三个图形它们不相邻。
故选:D
【分析】解答此题要根据展开图中圆与正方形相邻的特点,具备这个特点只有第四个图形。
20.【答案】A,E,F
【解析】【解答】解:正方体展开后有6个正方形的面,因此A是正方体的展开图;第二个物体展开后是4个三角形,因此E是它的展开图,长方体展开后有6个面,因此F是长方体的展开图.
故答案为:A,E,F
【分析】观察着几个物体展开后有几个面,根据面的个数及面的形状判断哪些图形可以折成圆圈中的图形即可.
三、应用题
21.【答案】解:连线如下:
【解析】【分析】结合圆柱、长方体、圆锥展开图的特点进行连线.注意圆柱是上下两个圆形的底面和一个长方形侧面组成,长方体是六个长方形组成,圆锥是一个扇形和一个底面圆组成.考查了立体图形的展开图,熟记常见立体图形的平面展开图的特征是解决此类问题的关键.
22.【答案】解:长方体的长是30厘米,宽是30厘米,高是12厘米,
表面积为:
30×12×4+30×30
=1440+900
=2340(平方厘米)
体积为:30×30×12=10800(立方厘米).
答:做这个纸盒需要2340平方厘米的纸板;这个纸盒的容积是10800立方厘米.
【解析】【分析】由展开图得出长方体的长是30厘米,宽是30厘米,高是12厘米;再根据长方体表面积和体积的公式计算即可.解决本题的关键是根据展开图找出长方体的长、宽、高,再根据表面积公式和体积公式计算即可.
23.【答案】解:20÷4=5(厘米),
5×5×20
=25×20
=500(立方厘米),
答:这个长方体的体积是500立方厘米.
【解析】【分析】根据题意可知:这个长方体的底面周长和高相等,首先用底面周长除以4求出底面边长,再根据长方体的体积公式解答即可.此题主要考查长方体的体积公式的灵活运用.
24.【答案】解:(1)(20﹣8)÷2=6(厘米)
(10×8+10×6+8×6)×2
=(80+60+48)×2
=188×2
=376(平方厘米)
答:表面积是376平方厘米.
(2)10×8×6=480(立方厘米)
答:体积是480立方厘米.
【解析】【分析】由展开图得出长方体的长是10厘米,宽是8厘米,高是(20﹣8)÷2=6(厘米),再根据长方体表面积=长×宽×2+长×高×2+宽×高×2;长方体体积=长×宽×高,计算即可.解决本题的关键是根据展开图找出长方体的长、宽、高,再根据表面积公式和体积公式计算即可.
25.【答案】解:在展开图上找出相对的面,并用上、下、左、右标出,再用a,b,c标出每条棱(下图)
【解析】【分析】根据长方体展开图的特征,右图属于左图的展开图,展开后相同颜色的面为相对的面,根据相对面的长、宽分别相等,由左图所标出的各棱,即可在右图中分别并用上、下、左、右标出,再用a,b,c标出每条棱.此题是考查长方体展开图的特征,长方体展开图与正方体展开图类似,但要复杂,正方体展开图的六相面是相等的正方形,长方体展开图对面是相同的长方形形(特殊长方体有一组对面是正方形,其余是四个相同的长方形).
