必修1 第一章 1.3《函数的单调性》课件(共29张PPT)
文档属性
| 名称 | 必修1 第一章 1.3《函数的单调性》课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
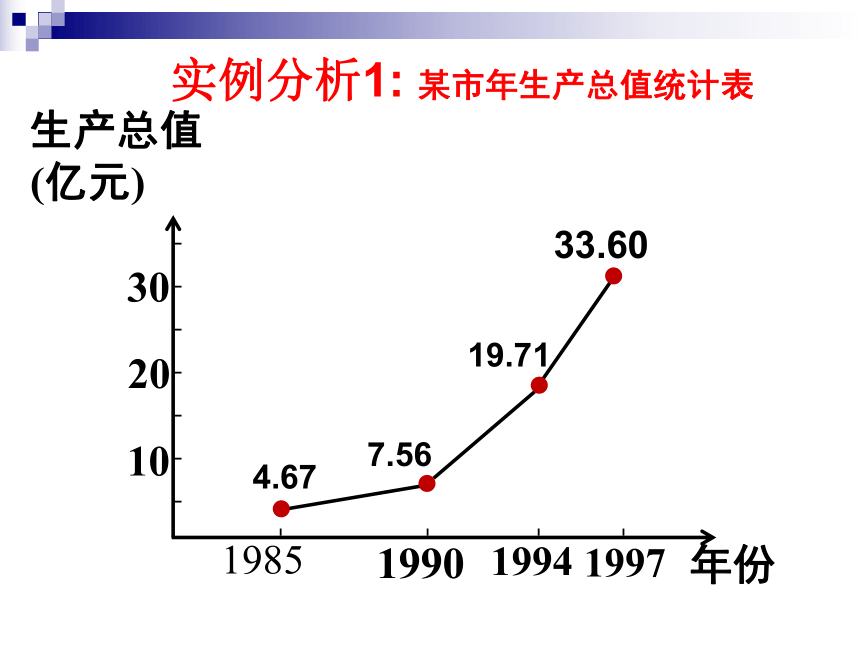
实例分析1:
某市年生产总值统计表
生产总值
(亿元)
年份
30
20
10
33.60
19.71
7.56
4.67
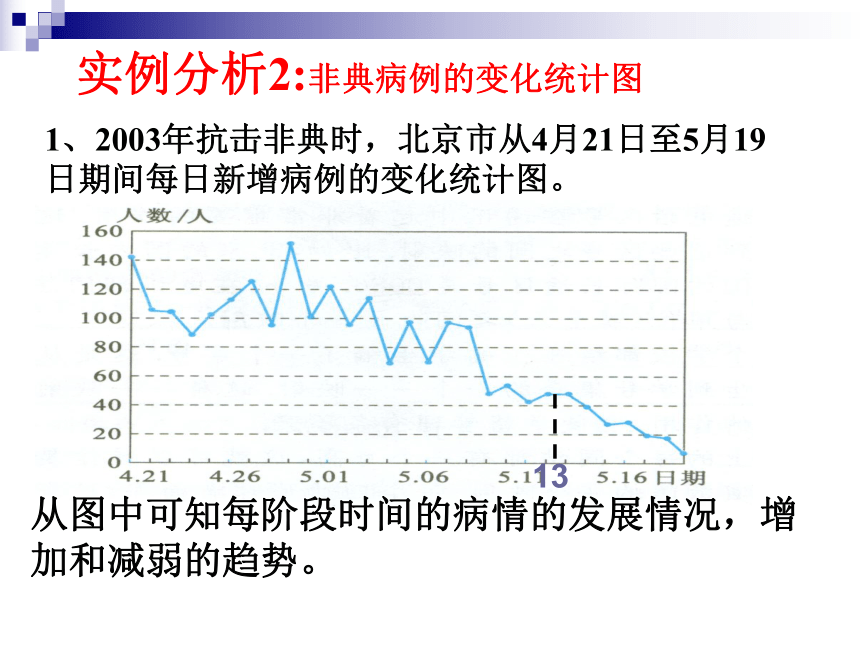
实例分析2:非典病例的变化统计图
1、2003年抗击非典时,北京市从4月21日至5月19日期间每日新增病例的变化统计图。
从图中可知每阶段时间的病情的发展情况,增加和减弱的趋势。
13
数与形,本是相倚依
焉能分作两边飞
数无形时少直觉
形少数时难入微
数形结合百般好
隔离分家万事休
切莫忘,几何代数统一体
永远联系莫分离
——
华罗庚
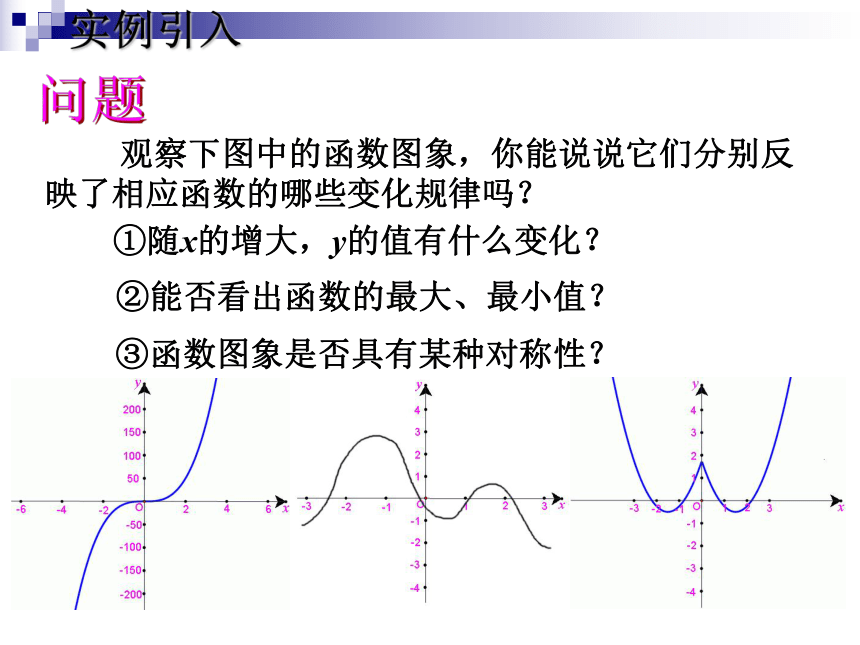
观察下图中的函数图象,你能说说它们分别反映了相应函数的哪些变化规律吗?
实例引入
①随x的增大,y的值有什么变化?
②能否看出函数的最大、最小值?
③函数图象是否具有某种对称性?
x
y
o
x
o
1
1
1
-1
y=x+1
y=-x+1
y
随
x
的增大而增大
y
随
x
的增大而减小
y
x
y
o
y
=
x2
1.
观察函数图象,从左向右函数图象如何变化?
2.
针对函数y=x2在[0,+∞
)上图像,任取自
变量的两个值,比较其对应函数值的大小.
3.
总结归纳出函数图象中自变量x和
y值之间的变化规律.
x
y
o
y
=
x2
在[0,+∞)上y
随
x
的增大而增大
在(-∞,0]上
y
随
x
的增大而减小
o
一般地,设函数
的定义域为I:
如果对于属于定义域I内某个区间上的任意两个自变量的值
,
。当
时,都有
那么就说
在这个区间上是增函数。
o
一般地,设函数
的定义域为I:
如果对于属于定义域I内某个区间上的任意两个自变量的值
,
。当
时,都有
那么就说
在这个区间上是减函数。
如果函数
在某个区间上是增
函数或减函数,那么就说函数
在这一区间具有(严格的)单调性,
这一区间叫做
的单调区间。
函数的单调性也叫函
数的增减性
函数的单调性是对定义域内某个区间
而言的,它是函数的
局部性质.
注:
例1:下图是定义在闭区间[-5,5]上的函
数
的图象,根据图象说出
的单调区间,以及在每一区间上,
是增函数还是减函数.
-2
1
2
3
4
5
-2
3
-3
-4
-5
-1
-1
1
2
O
-2
1
2
3
4
5
-2
3
-3
-4
-5
-1
-1
1
2
在区间[-5,-2),
[1,3)上是减函数
在区间[-2,1),
[3,5)上是增函数.
解:函数
的单调区间有
[-5,-2),
[-2,1),
[1,3),
[3,5],
O
练习:如图,已知
的图象(包括端点),根据图象说出函数的单调区间,以及在每一区间上,函数是增函数还是减函数.
-1
1
o
2.根据图象说出函数的的单调区间,以及在每一单调区间上,函数是增函数还是减函数.
y
1
2
3
4
5
x
y=(x)
-1
O
例2、物理学中的玻意耳定律
告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大。试用函数的单调性证明之。
证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1由V1,V2∈
(0,+∞)且V10,
V2-
V1
>0
又k>0,于是
所以,函数
是减函数.也就是说,当体积V减少时,压强p将增大.
取值
定号
变形
作差
结论
判断函数单调性的方法步骤
利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:
①任取x1,x2∈D,且x1②作差f(x1)-f(x2);
③变形
④定号(即判断差f(x1)-f(x2)的正负);
⑤下结论(即指出函数f(x)在给定的区间D上的单调性).
(通常是因式分解和配方);
练习:证明函数
在R上是
增函数.
证明:设x1,x2是R上的任意两个实数,
且x1
<
x2
,则
f(x1)-f(x2)=(3
x1
+2)-(3
x2
+2)
=3(x1
-
x2).
由x1
<
x2
,得x1
-
x2
<0,
于是f(x1)-f(x2)<0,即f(x1)所以,
f(x)=3x+2在R上是增函数.
任意取值
作差变形
判断符号
得出结论
例3.画出下列函数图像,并写出单调区间:
x
y
_____________
,
讨论1:根据函数单调性的定义,
?
1、判断f(x)=x2-1在(0,+
∞)上是增函数还是减函数?
2、判断f(x)=-x2+2x在(-
∞,0)上是增函数还是减函数?
练习
增函数
增函数
O
x
y
2
1
单调增区间
单调减区间
a>0
a<0
的对称轴为
小
结
1、函数单调性是对定义域的某个区间而言的,反映的是在这一区间上函数值随自变量变化的性质,
是函数的局部性质。
2、判断函数单调性的方法:
(1)利用图象:
在单调区间上,增函数图象从左向右是上升的,减函数图象是下降的.
(2)利用定义:
用定义证明函数单调性的一般步骤:
任意取值→作差变形→判断符号→
得出结论.
课堂小结,知识再现
实例分析1:
某市年生产总值统计表
生产总值
(亿元)
年份
30
20
10
33.60
19.71
7.56
4.67
实例分析2:非典病例的变化统计图
1、2003年抗击非典时,北京市从4月21日至5月19日期间每日新增病例的变化统计图。
从图中可知每阶段时间的病情的发展情况,增加和减弱的趋势。
13
数与形,本是相倚依
焉能分作两边飞
数无形时少直觉
形少数时难入微
数形结合百般好
隔离分家万事休
切莫忘,几何代数统一体
永远联系莫分离
——
华罗庚
观察下图中的函数图象,你能说说它们分别反映了相应函数的哪些变化规律吗?
实例引入
①随x的增大,y的值有什么变化?
②能否看出函数的最大、最小值?
③函数图象是否具有某种对称性?
x
y
o
x
o
1
1
1
-1
y=x+1
y=-x+1
y
随
x
的增大而增大
y
随
x
的增大而减小
y
x
y
o
y
=
x2
1.
观察函数图象,从左向右函数图象如何变化?
2.
针对函数y=x2在[0,+∞
)上图像,任取自
变量的两个值,比较其对应函数值的大小.
3.
总结归纳出函数图象中自变量x和
y值之间的变化规律.
x
y
o
y
=
x2
在[0,+∞)上y
随
x
的增大而增大
在(-∞,0]上
y
随
x
的增大而减小
o
一般地,设函数
的定义域为I:
如果对于属于定义域I内某个区间上的任意两个自变量的值
,
。当
时,都有
那么就说
在这个区间上是增函数。
o
一般地,设函数
的定义域为I:
如果对于属于定义域I内某个区间上的任意两个自变量的值
,
。当
时,都有
那么就说
在这个区间上是减函数。
如果函数
在某个区间上是增
函数或减函数,那么就说函数
在这一区间具有(严格的)单调性,
这一区间叫做
的单调区间。
函数的单调性也叫函
数的增减性
函数的单调性是对定义域内某个区间
而言的,它是函数的
局部性质.
注:
例1:下图是定义在闭区间[-5,5]上的函
数
的图象,根据图象说出
的单调区间,以及在每一区间上,
是增函数还是减函数.
-2
1
2
3
4
5
-2
3
-3
-4
-5
-1
-1
1
2
O
-2
1
2
3
4
5
-2
3
-3
-4
-5
-1
-1
1
2
在区间[-5,-2),
[1,3)上是减函数
在区间[-2,1),
[3,5)上是增函数.
解:函数
的单调区间有
[-5,-2),
[-2,1),
[1,3),
[3,5],
O
练习:如图,已知
的图象(包括端点),根据图象说出函数的单调区间,以及在每一区间上,函数是增函数还是减函数.
-1
1
o
2.根据图象说出函数的的单调区间,以及在每一单调区间上,函数是增函数还是减函数.
y
1
2
3
4
5
x
y=(x)
-1
O
例2、物理学中的玻意耳定律
告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大。试用函数的单调性证明之。
证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1
(0,+∞)且V1
V2-
V1
>0
又k>0,于是
所以,函数
是减函数.也就是说,当体积V减少时,压强p将增大.
取值
定号
变形
作差
结论
判断函数单调性的方法步骤
利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:
①任取x1,x2∈D,且x1
③变形
④定号(即判断差f(x1)-f(x2)的正负);
⑤下结论(即指出函数f(x)在给定的区间D上的单调性).
(通常是因式分解和配方);
练习:证明函数
在R上是
增函数.
证明:设x1,x2是R上的任意两个实数,
且x1
<
x2
,则
f(x1)-f(x2)=(3
x1
+2)-(3
x2
+2)
=3(x1
-
x2).
由x1
<
x2
,得x1
-
x2
<0,
于是f(x1)-f(x2)<0,即f(x1)
f(x)=3x+2在R上是增函数.
任意取值
作差变形
判断符号
得出结论
例3.画出下列函数图像,并写出单调区间:
x
y
_____________
,
讨论1:根据函数单调性的定义,
?
1、判断f(x)=x2-1在(0,+
∞)上是增函数还是减函数?
2、判断f(x)=-x2+2x在(-
∞,0)上是增函数还是减函数?
练习
增函数
增函数
O
x
y
2
1
单调增区间
单调减区间
a>0
a<0
的对称轴为
小
结
1、函数单调性是对定义域的某个区间而言的,反映的是在这一区间上函数值随自变量变化的性质,
是函数的局部性质。
2、判断函数单调性的方法:
(1)利用图象:
在单调区间上,增函数图象从左向右是上升的,减函数图象是下降的.
(2)利用定义:
用定义证明函数单调性的一般步骤:
任意取值→作差变形→判断符号→
得出结论.
课堂小结,知识再现
