1.3.2函数的奇偶性(共28张PPT)
文档属性
| 名称 | 1.3.2函数的奇偶性(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
1.3.2函数的奇偶性
汉寿一中
郭晖霞
人教A版必修一第一章
复习引入:
复习引入:
如果一个图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴.
2.什么是中心对称图形?
在平面内,一个图形绕某个点旋转1800,能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
1.什么是轴对称图形?
复习引入:
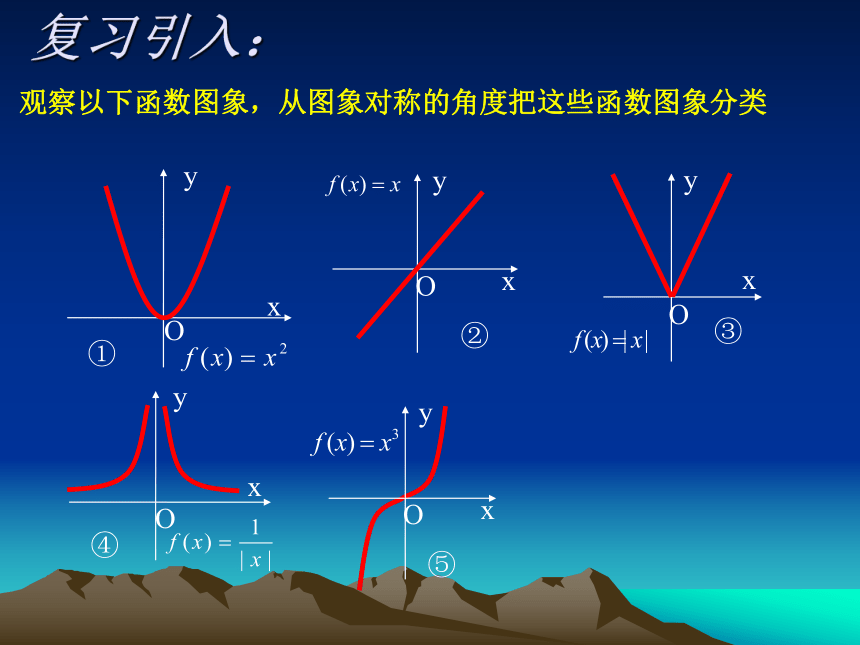
观察以下函数图象,从图象对称的角度把这些函数图象分类
O
x
y
①
②
O
x
y
③
O
x
y
④
O
x
y
O
x
y
⑤
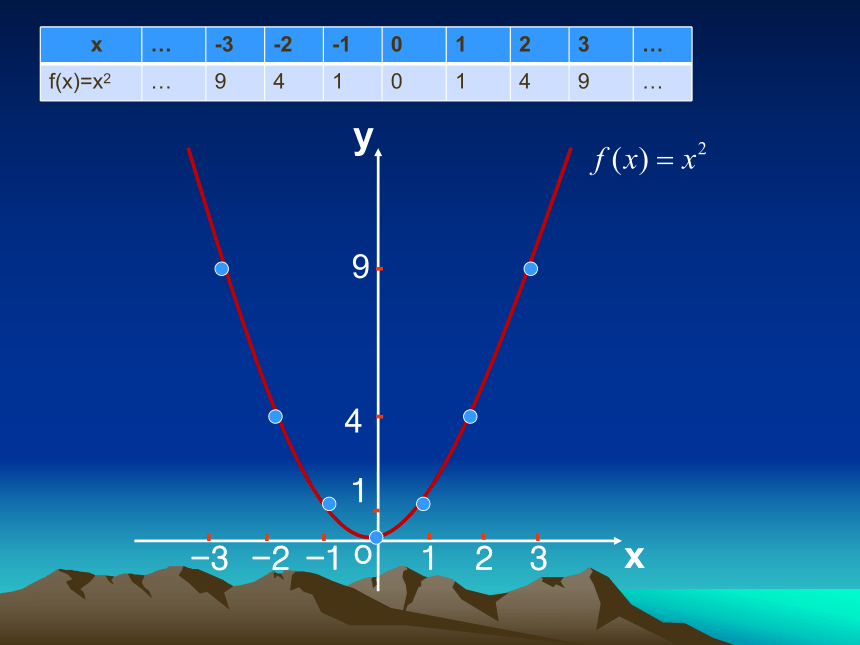
(1)请用列表法画出函数f(x)=x2与函数
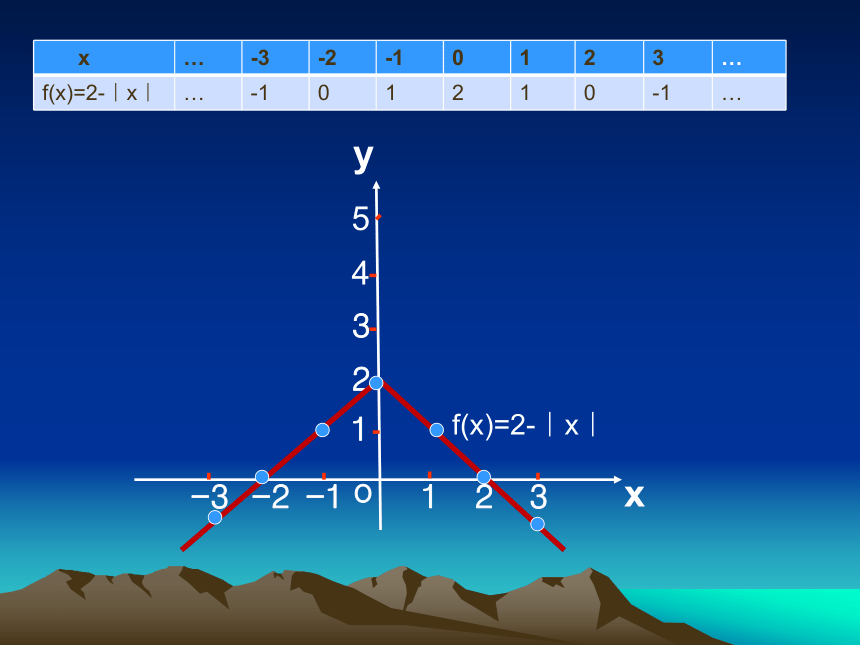
f(x)=2-
|
x
︱的图像
分组活动:
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x2
…
9
4
1
0
1
4
9
…
o
x
y
1
1
2
3
-2
-1
-3
4
9
x
…
-3
-2
-1
0
1
2
3
…
f(x)=2-|x|
…
-1
0
1
2
1
0
-1
…
o
x
y
1
1
2
3
-2
-1
-3
2
3
4
5
f(x)=2-|x|
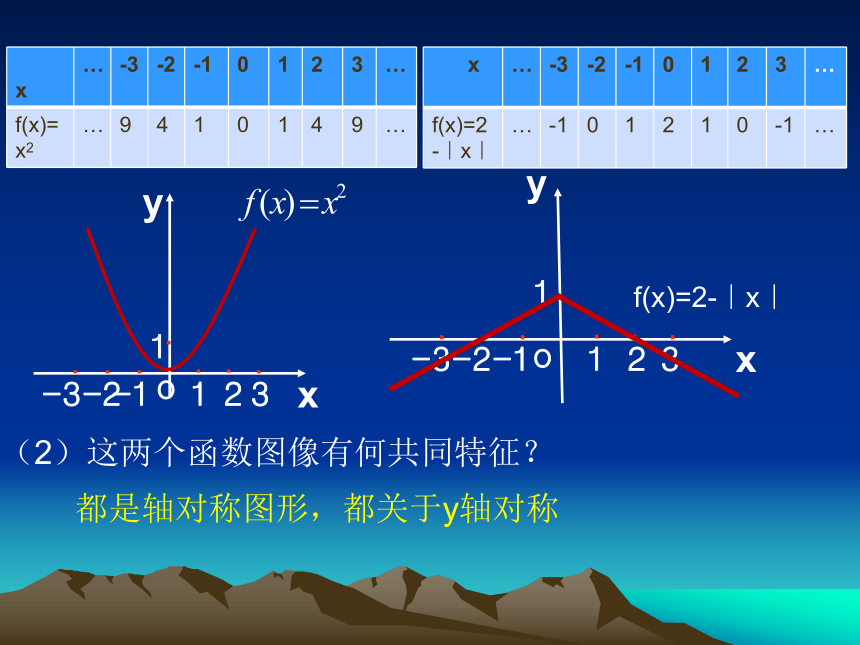
(2)这两个函数图像有何共同特征?
都是轴对称图形,都关于y轴对称
o
x
y
1
1
2
3
-2
-1
-3
o
x
y
1
1
2
3
-2
-1
-3
f(x)=2-|x|
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x2
…
9
4
1
0
1
4
9
…
x
…
-3
-2
-1
0
1
2
3
…
f(x)=2-|x|
…
-1
0
1
2
1
0
-1
…
o
x
y
1
1
2
3
-2
-1
-3
o
x
y
1
1
2
3
-2
-1
-3
f(x)=2-|x|
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x2
…
9
4
1
0
1
4
9
…
x
…
-3
-2
-1
0
1
2
3
…
f(x)=2-|x|
…
-1
0
1
2
1
0
-1
…
(3)从函数值对应表中能发现自变量与
函数值之间有什么关系?
自变量互为相反数时,函数值相等
y=x^2.gsp
2-abs(x).gsp
(1)观察下面的函数图象,是否关于关于y轴对称?
a
(2)如果一个函数的图象关于y轴对称,那么它的定义域应该有什么特点?
探究:
若函数图像关于y轴对称,则定义域应该关于原点对称.
偶函数
:设函数
的定义域为
D
,如果对定义域
D内的任意一个
x
都有-x
∈
D,
且
,则这个函数叫做偶函数.
建构新知:
偶函数图像关于y轴对称
随堂练习:
1.判断下列函数是否为偶函数?
(1)
(2)
(3)
2.偶函数定义域是[a,2a+3],则a=_____.
-1
类比迁移:
观察函数
与函数
的图像
并完成P34的函数值对应表.
1.这两个图像有什么共同特征?
2.自变量与函数值之间存在什么关系?
D:\y=x.gsp
D:\2图像.gsp
0
x
y
0
x
y
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x2
…
-3
-2
-1
0
1
2
3
…
x
…
-3
-2
-1
0
1
2
3
…
f(x)=2-|x|
…
-1
/
1
…
3.仿照偶函数概念的形成,给出奇函数的定义:
类比迁移:
奇函数:设函数
的定义域为
,如果对
内的任意一个
,都有
,且
,则这个函数叫奇函数.
奇函数图像关于原点对称
思考:
奇函数若在原点处有定义,f(0)=?
奇函数若在原点处有意义,则一定有f(0)=0
随堂练习:
1.判断下列函数是否为奇函数?
(1)
(2)
(3)
2.已知函数
为奇函数,则
m=_______.
对于奇、偶函数定义的几点说明:
(2)
定义域关于原点对称是函数具有奇偶性的先决条件。
(3)奇、偶函数定义的逆命题也成立,
即:若函数f(x)为奇函数,
则f(-x)=-f(x)成立。
若函数f(x)为偶函数,
则f(-x)=
f(x)
成立。
(1)
如果一个函数f(x)是奇函数或偶函数,那么我们就
是说函数f(x)
具有奇偶性。
例1.
用定义判断下列函数的奇偶性
(2)
f(x)=x2+1
(3)
(5)
f(x)=0
讲练结合,巩固新知:
(4)
f(x)=x2
[-1,3]
奇函数
偶函数
非奇非偶函数
既奇且偶函数
根据奇偶性,
函数可划分为四类:
例2.判断下列函数的奇偶性:
(3)
o
x
y
(1)
o
x
y
(4)
o
x
y
(2)
o
x
y
讲练结合,巩固新知:
偶函数
奇函数
非奇非偶函数
非奇非偶函数
奇偶函数的图象性质:
(1)奇函数图象关于原点对称;
(2)偶函数图象关于y轴对称。
奇偶函数的图象性质可用于解决:
(1)判断函数奇偶性;
(2)简化函数图象画法.
奇偶性
奇函数
偶函数
定
义
设函数y=f(x)的定义域为D,
,都有
.
f(-x)=-f(x)
f(-x)=f(x)
图
像
性
质
关于原点对称
关于y轴对称
判断
步骤
定义域是否关于原点对称.
f(-x)=-f(x)
f(-x)=f(x)
x
o
y
(a,f(a))
(-a,f(-a))
-a
a
x
o
y
-a
a
(a,f(a))
(-a,f(-a))
注:若奇函数在原点处有定义,则一定有f(0)=0
当堂小结:
课堂检测:
1.若定义在区间[a,5]
上的函数f(x)
为偶函数,则a=___.
2.
已知函数
是奇函数,则a
的值为(
)
A.-1
B.-2
C.1
D.2
?
3.
如果奇函数f(x)
在[3,7]
上是增函数,且最小值是5,那么
在f(x)在[-7,-3]
上是(
)
A增函数,最小值是-5
B增函数,最大值是-5
C减函数,最小值是-5
D减函数,最大值是-5
4.
判断下列函数是否具有奇偶性:
(1)
;
(2)
;
(3)
;
(4)
课后拓展:
已知f(x)是定义在R上的奇函数,且当x>0时,f(x)=x(1-x),
求:(1)x<0时,f(x)的解析式;
(2)
f(x)的解析式.
课后作业:
P39组3,B组3.
谢谢,再见!
1.3.2函数的奇偶性
汉寿一中
郭晖霞
人教A版必修一第一章
复习引入:
复习引入:
如果一个图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴.
2.什么是中心对称图形?
在平面内,一个图形绕某个点旋转1800,能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
1.什么是轴对称图形?
复习引入:
观察以下函数图象,从图象对称的角度把这些函数图象分类
O
x
y
①
②
O
x
y
③
O
x
y
④
O
x
y
O
x
y
⑤
(1)请用列表法画出函数f(x)=x2与函数
f(x)=2-
|
x
︱的图像
分组活动:
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x2
…
9
4
1
0
1
4
9
…
o
x
y
1
1
2
3
-2
-1
-3
4
9
x
…
-3
-2
-1
0
1
2
3
…
f(x)=2-|x|
…
-1
0
1
2
1
0
-1
…
o
x
y
1
1
2
3
-2
-1
-3
2
3
4
5
f(x)=2-|x|
(2)这两个函数图像有何共同特征?
都是轴对称图形,都关于y轴对称
o
x
y
1
1
2
3
-2
-1
-3
o
x
y
1
1
2
3
-2
-1
-3
f(x)=2-|x|
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x2
…
9
4
1
0
1
4
9
…
x
…
-3
-2
-1
0
1
2
3
…
f(x)=2-|x|
…
-1
0
1
2
1
0
-1
…
o
x
y
1
1
2
3
-2
-1
-3
o
x
y
1
1
2
3
-2
-1
-3
f(x)=2-|x|
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x2
…
9
4
1
0
1
4
9
…
x
…
-3
-2
-1
0
1
2
3
…
f(x)=2-|x|
…
-1
0
1
2
1
0
-1
…
(3)从函数值对应表中能发现自变量与
函数值之间有什么关系?
自变量互为相反数时,函数值相等
y=x^2.gsp
2-abs(x).gsp
(1)观察下面的函数图象,是否关于关于y轴对称?
a
(2)如果一个函数的图象关于y轴对称,那么它的定义域应该有什么特点?
探究:
若函数图像关于y轴对称,则定义域应该关于原点对称.
偶函数
:设函数
的定义域为
D
,如果对定义域
D内的任意一个
x
都有-x
∈
D,
且
,则这个函数叫做偶函数.
建构新知:
偶函数图像关于y轴对称
随堂练习:
1.判断下列函数是否为偶函数?
(1)
(2)
(3)
2.偶函数定义域是[a,2a+3],则a=_____.
-1
类比迁移:
观察函数
与函数
的图像
并完成P34的函数值对应表.
1.这两个图像有什么共同特征?
2.自变量与函数值之间存在什么关系?
D:\y=x.gsp
D:\2图像.gsp
0
x
y
0
x
y
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x2
…
-3
-2
-1
0
1
2
3
…
x
…
-3
-2
-1
0
1
2
3
…
f(x)=2-|x|
…
-1
/
1
…
3.仿照偶函数概念的形成,给出奇函数的定义:
类比迁移:
奇函数:设函数
的定义域为
,如果对
内的任意一个
,都有
,且
,则这个函数叫奇函数.
奇函数图像关于原点对称
思考:
奇函数若在原点处有定义,f(0)=?
奇函数若在原点处有意义,则一定有f(0)=0
随堂练习:
1.判断下列函数是否为奇函数?
(1)
(2)
(3)
2.已知函数
为奇函数,则
m=_______.
对于奇、偶函数定义的几点说明:
(2)
定义域关于原点对称是函数具有奇偶性的先决条件。
(3)奇、偶函数定义的逆命题也成立,
即:若函数f(x)为奇函数,
则f(-x)=-f(x)成立。
若函数f(x)为偶函数,
则f(-x)=
f(x)
成立。
(1)
如果一个函数f(x)是奇函数或偶函数,那么我们就
是说函数f(x)
具有奇偶性。
例1.
用定义判断下列函数的奇偶性
(2)
f(x)=x2+1
(3)
(5)
f(x)=0
讲练结合,巩固新知:
(4)
f(x)=x2
[-1,3]
奇函数
偶函数
非奇非偶函数
既奇且偶函数
根据奇偶性,
函数可划分为四类:
例2.判断下列函数的奇偶性:
(3)
o
x
y
(1)
o
x
y
(4)
o
x
y
(2)
o
x
y
讲练结合,巩固新知:
偶函数
奇函数
非奇非偶函数
非奇非偶函数
奇偶函数的图象性质:
(1)奇函数图象关于原点对称;
(2)偶函数图象关于y轴对称。
奇偶函数的图象性质可用于解决:
(1)判断函数奇偶性;
(2)简化函数图象画法.
奇偶性
奇函数
偶函数
定
义
设函数y=f(x)的定义域为D,
,都有
.
f(-x)=-f(x)
f(-x)=f(x)
图
像
性
质
关于原点对称
关于y轴对称
判断
步骤
定义域是否关于原点对称.
f(-x)=-f(x)
f(-x)=f(x)
x
o
y
(a,f(a))
(-a,f(-a))
-a
a
x
o
y
-a
a
(a,f(a))
(-a,f(-a))
注:若奇函数在原点处有定义,则一定有f(0)=0
当堂小结:
课堂检测:
1.若定义在区间[a,5]
上的函数f(x)
为偶函数,则a=___.
2.
已知函数
是奇函数,则a
的值为(
)
A.-1
B.-2
C.1
D.2
?
3.
如果奇函数f(x)
在[3,7]
上是增函数,且最小值是5,那么
在f(x)在[-7,-3]
上是(
)
A增函数,最小值是-5
B增函数,最大值是-5
C减函数,最小值是-5
D减函数,最大值是-5
4.
判断下列函数是否具有奇偶性:
(1)
;
(2)
;
(3)
;
(4)
课后拓展:
已知f(x)是定义在R上的奇函数,且当x>0时,f(x)=x(1-x),
求:(1)x<0时,f(x)的解析式;
(2)
f(x)的解析式.
课后作业:
P39组3,B组3.
谢谢,再见!
