7.2 坐标方法的简单应用 高频易错题汇编(含解析)
文档属性
| 名称 | 7.2 坐标方法的简单应用 高频易错题汇编(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 335.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 18:58:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
7.2 坐标方法的简单应用 高频易错题集
一.选择题(共10小题)
1.如图,五架轰炸机组成了一个三角形飞行编队,且每架飞机都在边长等于1正方形网格格点上,其中A、B两架轰炸机对应点的坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么轰炸机C对应点的坐标是( )
A.(2,﹣1) B.(4,﹣2) C.(4,2) D.(2,0)
2.某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是( )
A.第3组第2排 B.第3组第1排 C.第2组第3排 D.第2组第2排
3.已知点(3﹣2k2,4k﹣3)在第一象限的角平分线上,则k=( )
A.1 B.﹣1 C.0 D.0或1
4.已知点A(﹣1,﹣2)和点B(3,m﹣1),如果直线AB∥x轴,那么m的值为( )
A.1 B.﹣4 C.﹣1 D.3
5.对于直角坐标平面内的任意两点A(x1,y1),B(x2,y2),定义它们之间的一种“距离”:
||AB||=|x2﹣x1|+|y2﹣y1|.给出下列三个命题:
①若点C在线段AB上,则||AC||+||CB||=||AB||;
②在△ABC中,若∠C=90°,则||AC||2+||CB||2=||AB||2;
③在△ABC中,||AC||+||CB||>||AB||.其中真命题的个数为( )
A.0 B.1 C.2 D.3
6.如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(﹣2,2),第四次向右跳动5个单位至点A4(3,2),…,以此规律跳动下去,点A第2020次跳动至点A2020的坐标是( )
A.(1012,1011) B.(1009,1008)
C.(1010,1009) D.(1011,1010)
7.将点P(2m+3,m﹣2)向上平移2个单位得到P′,且P′在x轴上,那么点P的坐标是( )
A.(3,﹣2) B.(3,0) C.(7,0) D.(9,1)
8.将某图形的各顶点的横坐标保持不变,纵坐标减去3,可将该图形( )
A.横向向右平移3个单位 B.横向向左平移3个单位
C.纵向向上平移3个单位 D.纵向向下平移3个单位
9.已知坐标平面内的点A(﹣2,4),如果将平面直角坐标系向左平移3个单位长度,再向上平移2个单位长度,那么平移后点A的坐标是( )
A.(1,6) B.(﹣5,6) C.(﹣5,2) D.(1,2)
10.线段AB经过平移得到线段CD,其中点A、B的对应点分别为点C、D,这四个点都在如图所示的格点上,那么线段AB上的一点P(a,b)经过平移后,在线段CD上的对应点Q的坐标是( )
A.(a﹣1,b+3) B.(a﹣1,b﹣3) C.(a+1,b+3) D.(a+1,b﹣3)
二.填空题(共5小题)
11.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动一个单位,依次得到点P1(0,1);P2(1,1);P3(1,0);P4(1,﹣1);P5(2,﹣1);P6(2,0)……,则点P2019的坐标是 .
12.如图,在围棋盘上有三枚棋子,如果黑棋①的位置用坐标表为(0,﹣1),黑棋②的位置用坐标表示为(﹣3,0),则白棋③坐标表示为
13.平面直角坐标系中,已知点A(a,3),点B(2,b),若线段AB被y轴垂直平分,则a+b= .
14.将点P(﹣1,2)向左平移2个单位,再向上平移1个单位所得的对应点的坐标为 .
15.已知点M(a﹣1,5),现在将平面直角坐标系先向左平移3个单位,之后又向下平移4个单位,得到点N(2,b﹣1),则a= ,b= .
三.解答题(共5小题)
16.如图所示,是一个围棋盘的平面示意图(每个小正方形边长为1个单位长度)
(1)已知白棋②的坐标为(﹣1,1),写出白棋④的坐标和黑棋的坐标;
(2)若白棋②的坐标为(3,1),则白棋④的坐标和黑棋的坐标是否发生改变?若改变,请写出坐标;若不改变,请说明理由.
17.如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周)
(1)写出点B的坐标( , );
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴距离为4个单位长度时,求点P移动的时间.
18.先阅读下列一段文字,再解答问题
已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|
(1)已知点A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点间的距离;
(3)已知点A(0,6)B(﹣3,2),C(3,2),判断线段AB,BC,AC中哪两条是相等的?并说明理由.
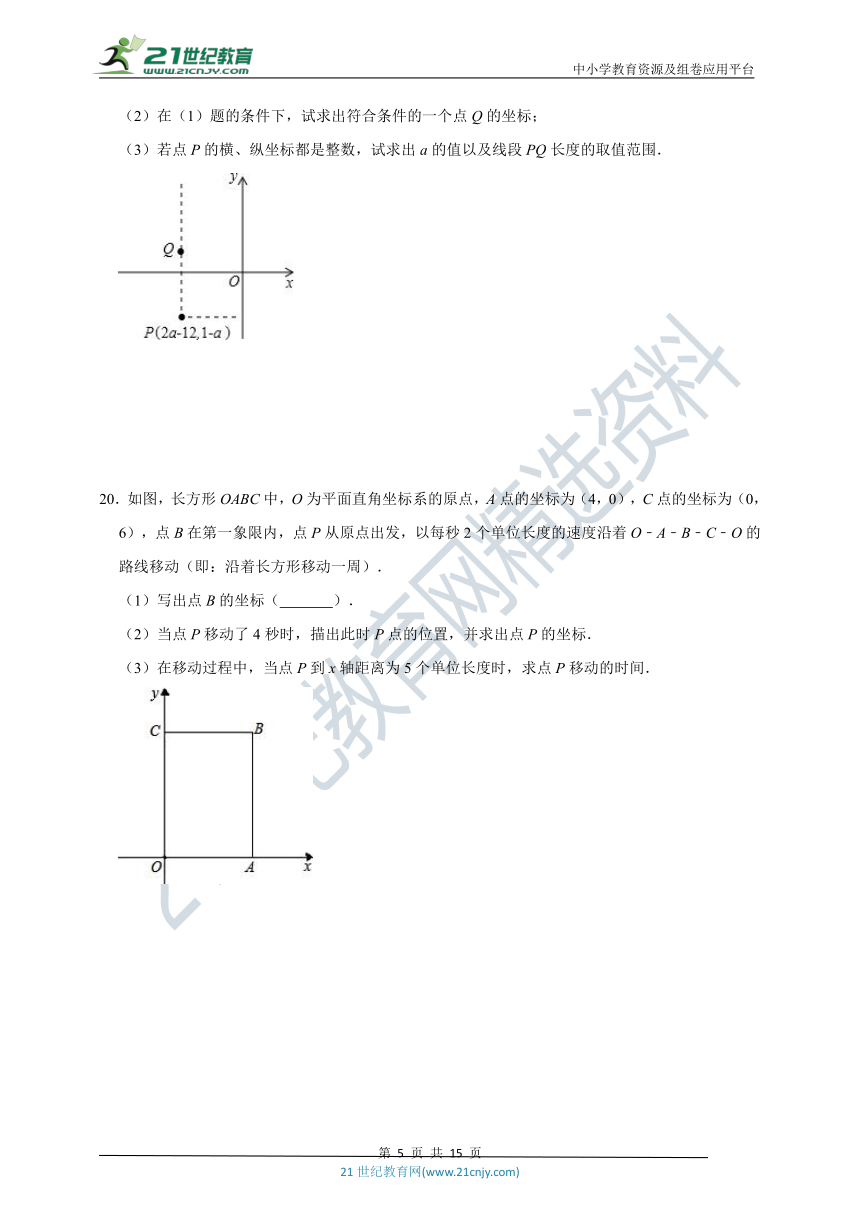
19.已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值;
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
20.如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线移动(即:沿着长方形移动一周).
(1)写出点B的坐标( ).
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
7.2 坐标方法的简单应用 高频易错题集
试题解析
一.选择题(共10小题)
1.如图,五架轰炸机组成了一个三角形飞行编队,且每架飞机都在边长等于1正方形网格格点上,其中A、B两架轰炸机对应点的坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么轰炸机C对应点的坐标是( )
A.(2,﹣1) B.(4,﹣2) C.(4,2) D.(2,0)
解:因为A(﹣2,1)和B(﹣2,﹣3),
所以建立如图所示的坐标系,可得点C的坐标为(2,﹣1),
故选:A.
2.某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是( )
A.第3组第2排 B.第3组第1排 C.第2组第3排 D.第2组第2排
解:某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是第2组第3排,
故选:C.
3.已知点(3﹣2k2,4k﹣3)在第一象限的角平分线上,则k=( )
A.1 B.﹣1 C.0 D.0或1
解:∵点(3﹣2k2,4k﹣3)在第一象限的角平分线上,
∴3﹣2k2=4k﹣3,
整理得,k2+2k﹣3=0,
解得k1=﹣3,k2=1,
当k=﹣3时,3﹣2×(﹣3)2=﹣15,
点为(﹣15,﹣15),在第三象限,舍去;
当k=1时,3﹣2×12=1,
点为(1,1),在第一象限,
所以k=1.
故选:A.
4.已知点A(﹣1,﹣2)和点B(3,m﹣1),如果直线AB∥x轴,那么m的值为( )
A.1 B.﹣4 C.﹣1 D.3
解:∵点A(﹣1,﹣2)和点B(3,m﹣1),直线AB∥x轴,
∴﹣2=m﹣1,
∴m=﹣1,
故选:C.
5.对于直角坐标平面内的任意两点A(x1,y1),B(x2,y2),定义它们之间的一种“距离”:
||AB||=|x2﹣x1|+|y2﹣y1|.给出下列三个命题:
①若点C在线段AB上,则||AC||+||CB||=||AB||;
②在△ABC中,若∠C=90°,则||AC||2+||CB||2=||AB||2;
③在△ABC中,||AC||+||CB||>||AB||.其中真命题的个数为( )
A.0 B.1 C.2 D.3
解:对于直角坐标平面内的任意两点A(x1,y1),B(x2,y2),
定义它们之间的一种“距离”:||AB||=|x2﹣x1|+|y2﹣y1|.
对于①若点C在线段AB上,设C点坐标为(x0,y0),x0在x1、x2之间,y0在y1、y2之间,
则||AC||+||CB||=|x0﹣x1|+|y0﹣y1|+|x2﹣x0|+|y2﹣y0|=|x2﹣x1|+|y2﹣y1|=||AB||成立,故①正确.
对于②平方后不能消除x0,y0,命题不成立;
对于③在△ABC中,||AC||+||CB||=|x0﹣x1|+|y0﹣y1|+|x2﹣x0|+|y2﹣y0|≥|(x0﹣x1)+(x2﹣x0)|+|(y0﹣y1)+(y2﹣y0)|=|x2﹣x1|+|y2﹣y1|=||AB||.③不一定成立
∴命题①成立,
故选:B.
6.如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(﹣2,2),第四次向右跳动5个单位至点A4(3,2),…,以此规律跳动下去,点A第2020次跳动至点A2020的坐标是( )
A.(1012,1011) B.(1009,1008)
C.(1010,1009) D.(1011,1010)
解:因为A1(﹣1,1),A2(2,1)
A3(﹣2,2)A4(3,2)
A5(﹣3,3)A6(4,3)
A7(﹣4,4)A8(5,4)
…
A2n﹣1(﹣n,n) A2n(n+1,n)(n为正整数)
所以2n=2020,
n=1010
所以A2020(1011,1010)
故选:D.
7.将点P(2m+3,m﹣2)向上平移2个单位得到P′,且P′在x轴上,那么点P的坐标是( )
A.(3,﹣2) B.(3,0) C.(7,0) D.(9,1)
解:∵将点P(2m+3,m﹣2)向上平移2个单位得到P′,
∴P′的坐标为(2m+3,m),
∵P′在x轴上,
∴m=0,
∴点P的坐标是(3,﹣2).
故选:A.
8.将某图形的各顶点的横坐标保持不变,纵坐标减去3,可将该图形( )
A.横向向右平移3个单位 B.横向向左平移3个单位
C.纵向向上平移3个单位 D.纵向向下平移3个单位
解:∵某图形的各顶点的横坐标保持不变,纵坐标减去3,
∴将该图形向下平移了3个单位.
故选:D.
9.已知坐标平面内的点A(﹣2,4),如果将平面直角坐标系向左平移3个单位长度,再向上平移2个单位长度,那么平移后点A的坐标是( )
A.(1,6) B.(﹣5,6) C.(﹣5,2) D.(1,2)
解:∵坐标平面内点A(﹣2,4),将坐标系先向左平移3个单位长度,再向上平移2个单位长度,
∴点A的横坐标增大3,纵坐标减小2,
∴点A变化后的坐标为(1,2).
故选:D.
10.线段AB经过平移得到线段CD,其中点A、B的对应点分别为点C、D,这四个点都在如图所示的格点上,那么线段AB上的一点P(a,b)经过平移后,在线段CD上的对应点Q的坐标是( )
A.(a﹣1,b+3) B.(a﹣1,b﹣3) C.(a+1,b+3) D.(a+1,b﹣3)
解:由图可得,点A、B的对应点分别为点C、D,而B(1,3),D(2,0),
∴线段AB向右平移1个单位,向下平移3个单位得到线段CD,
又∵P(a,b),
∴Q(a+1,b﹣3),
故选:D.
二.填空题(共5小题)
11.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动一个单位,依次得到点P1(0,1);P2(1,1);P3(1,0);P4(1,﹣1);P5(2,﹣1);P6(2,0)……,则点P2019的坐标是 (673,0) .
解:由P3、P6、P9 可得规律:当下标为3的整数倍时,横坐标为,纵坐标为0,
∵2019÷3=673,
∴P2019 (673,0)
则点P2019的坐标是 (673,0).
故答案为 (673,0).
12.如图,在围棋盘上有三枚棋子,如果黑棋①的位置用坐标表为(0,﹣1),黑棋②的位置用坐标表示为(﹣3,0),则白棋③坐标表示为 (﹣4,2)
解:黑棋①的位置用坐标表为(0,﹣1),黑棋②的位置用坐标表示为(﹣3,0),可建立平面直角坐标系,如图,
∴白棋③的坐标为(﹣4,2).
故答案为:(﹣4,2).
13.平面直角坐标系中,已知点A(a,3),点B(2,b),若线段AB被y轴垂直平分,则a+b= 1 .
解:∵线段AB被y轴垂直平分,
∴点A(a,3)与点B(2,b)关于y轴对称,
∴a=﹣2,b=3,
∴a+b=﹣2+3=1.
故答案为:1.
14.将点P(﹣1,2)向左平移2个单位,再向上平移1个单位所得的对应点的坐标为 (﹣3,3) .
解:点P(﹣1,2)向左平移2个单位,再向上平移1个单位所得的对应点的坐标为(﹣1﹣2,2+1),即对应点的坐标是(﹣3,3).
故答案填:(﹣3,3).
15.已知点M(a﹣1,5),现在将平面直角坐标系先向左平移3个单位,之后又向下平移4个单位,得到点N(2,b﹣1),则a= 0 ,b= 10 .
解:由题意得a﹣1+3=2;5+4=b﹣1
解得a=0;b=10,
故答案为0;10.
三.解答题(共5小题)
16.如图所示,是一个围棋盘的平面示意图(每个小正方形边长为1个单位长度)
(1)已知白棋②的坐标为(﹣1,1),写出白棋④的坐标和黑棋的坐标;
(2)若白棋②的坐标为(3,1),则白棋④的坐标和黑棋的坐标是否发生改变?若改变,请写出坐标;若不改变,请说明理由.
解:(1)根据白棋②的坐标为(﹣1,1),如图所示,建立直角坐标系,则白棋④的坐标为(0,﹣3),黑棋的坐标为(3,﹣2);
(2)根据白棋②的坐标为(3,1),白棋④的坐标和黑棋的坐标发生改变,
如图所示,建立直角坐标系,则白棋④的坐标为(4,﹣3),黑棋的坐标为(7,﹣2);
17.如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周)
(1)写出点B的坐标( 4 , 5 );
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴距离为4个单位长度时,求点P移动的时间.
解:(1)点B的坐标(4,5),故答案为:4,5;
(2)当点P移动了4秒时,点P移动了4×2=8个单位长度,
∵C点的坐标为(0,5),∴OC=5,∴8﹣5=3,
∴此时,点P的位置在线段BC上,且CP=3,
如图所示,点P的坐标为BC边中点(3,5).
(3)当点P在OC上时,OP=4,
此时所用时间为4÷2=2(s);
当点P在AB上时,AP=4,BP=1,
∵A点的坐标为(4,0)∴OA=CB=4,
∵C点的坐标为(0,5)∴OC=5,OC+CB+BP=5+4+1=10,此时所用时间为
10÷2=5(s);
综上所述,当点P移动2秒或5秒时,点P到x轴的距离为4个单位长度.
18.先阅读下列一段文字,再解答问题
已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|
(1)已知点A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点间的距离;
(3)已知点A(0,6)B(﹣3,2),C(3,2),判断线段AB,BC,AC中哪两条是相等的?并说明理由.
解:(1)依据两点间的距离公式,可得AB==13;
(2)当点A,B在平行于y轴的直线上时,AB=|﹣1﹣5|=6;
(3)AB与AC相等.理由:
∵AB==5;
AC==5;
BC=|3﹣(﹣3)|=6.
∴AB=AC.
19.已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值;
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
解:
(1)1﹣a=﹣3,a=4.
(2)由a=4得:2a﹣12=2×4﹣12=﹣4,又点Q(x,y)位于第二象限,所以y>0;
取y=1,得点Q的坐标为(﹣4,1).
(3)因为点P(2a﹣12,1﹣a)位于第三象限,
所以,
解得:1<a<6.
因为点P的横、纵坐标都是整数,所以a=2或3或4或5;
当a=2时,1﹣a=﹣1,所以PQ>1;
当a=3时,1﹣a=﹣2,所以PQ>2;
当a=4时,1﹣a=﹣3,所以PQ>3;
当a=5时,1﹣a=﹣4,所以PQ>4.
20.如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线移动(即:沿着长方形移动一周).
(1)写出点B的坐标( 4,6 ).
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
解:(1)根据长方形的性质,可得AB与y轴平行,BC与x轴平行;
故B的坐标为(4,6);
故答案为:(4,6);
(2)根据题意,P的运动速度为每秒2个单位长度,
当点P移动了4秒时,则其运动了8个长度单位,
此时P的坐标为(4,4),位于AB上;
(3)根据题意,点P到x轴距离为5个单位长度时,有两种情况:
P在AB上时,P运动了4+5=9个长度单位,此时P运动了4.5秒;
P在OC上时,P运动了4+6+4+1=15个长度单位,此时P运动了=7.5秒.
_21?????????è?????(www.21cnjy.com)_
7.2 坐标方法的简单应用 高频易错题集
一.选择题(共10小题)
1.如图,五架轰炸机组成了一个三角形飞行编队,且每架飞机都在边长等于1正方形网格格点上,其中A、B两架轰炸机对应点的坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么轰炸机C对应点的坐标是( )
A.(2,﹣1) B.(4,﹣2) C.(4,2) D.(2,0)
2.某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是( )
A.第3组第2排 B.第3组第1排 C.第2组第3排 D.第2组第2排
3.已知点(3﹣2k2,4k﹣3)在第一象限的角平分线上,则k=( )
A.1 B.﹣1 C.0 D.0或1
4.已知点A(﹣1,﹣2)和点B(3,m﹣1),如果直线AB∥x轴,那么m的值为( )
A.1 B.﹣4 C.﹣1 D.3
5.对于直角坐标平面内的任意两点A(x1,y1),B(x2,y2),定义它们之间的一种“距离”:
||AB||=|x2﹣x1|+|y2﹣y1|.给出下列三个命题:
①若点C在线段AB上,则||AC||+||CB||=||AB||;
②在△ABC中,若∠C=90°,则||AC||2+||CB||2=||AB||2;
③在△ABC中,||AC||+||CB||>||AB||.其中真命题的个数为( )
A.0 B.1 C.2 D.3
6.如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(﹣2,2),第四次向右跳动5个单位至点A4(3,2),…,以此规律跳动下去,点A第2020次跳动至点A2020的坐标是( )
A.(1012,1011) B.(1009,1008)
C.(1010,1009) D.(1011,1010)
7.将点P(2m+3,m﹣2)向上平移2个单位得到P′,且P′在x轴上,那么点P的坐标是( )
A.(3,﹣2) B.(3,0) C.(7,0) D.(9,1)
8.将某图形的各顶点的横坐标保持不变,纵坐标减去3,可将该图形( )
A.横向向右平移3个单位 B.横向向左平移3个单位
C.纵向向上平移3个单位 D.纵向向下平移3个单位
9.已知坐标平面内的点A(﹣2,4),如果将平面直角坐标系向左平移3个单位长度,再向上平移2个单位长度,那么平移后点A的坐标是( )
A.(1,6) B.(﹣5,6) C.(﹣5,2) D.(1,2)
10.线段AB经过平移得到线段CD,其中点A、B的对应点分别为点C、D,这四个点都在如图所示的格点上,那么线段AB上的一点P(a,b)经过平移后,在线段CD上的对应点Q的坐标是( )
A.(a﹣1,b+3) B.(a﹣1,b﹣3) C.(a+1,b+3) D.(a+1,b﹣3)
二.填空题(共5小题)
11.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动一个单位,依次得到点P1(0,1);P2(1,1);P3(1,0);P4(1,﹣1);P5(2,﹣1);P6(2,0)……,则点P2019的坐标是 .
12.如图,在围棋盘上有三枚棋子,如果黑棋①的位置用坐标表为(0,﹣1),黑棋②的位置用坐标表示为(﹣3,0),则白棋③坐标表示为
13.平面直角坐标系中,已知点A(a,3),点B(2,b),若线段AB被y轴垂直平分,则a+b= .
14.将点P(﹣1,2)向左平移2个单位,再向上平移1个单位所得的对应点的坐标为 .
15.已知点M(a﹣1,5),现在将平面直角坐标系先向左平移3个单位,之后又向下平移4个单位,得到点N(2,b﹣1),则a= ,b= .
三.解答题(共5小题)
16.如图所示,是一个围棋盘的平面示意图(每个小正方形边长为1个单位长度)
(1)已知白棋②的坐标为(﹣1,1),写出白棋④的坐标和黑棋的坐标;
(2)若白棋②的坐标为(3,1),则白棋④的坐标和黑棋的坐标是否发生改变?若改变,请写出坐标;若不改变,请说明理由.
17.如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周)
(1)写出点B的坐标( , );
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴距离为4个单位长度时,求点P移动的时间.
18.先阅读下列一段文字,再解答问题
已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|
(1)已知点A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点间的距离;
(3)已知点A(0,6)B(﹣3,2),C(3,2),判断线段AB,BC,AC中哪两条是相等的?并说明理由.
19.已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值;
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
20.如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线移动(即:沿着长方形移动一周).
(1)写出点B的坐标( ).
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
7.2 坐标方法的简单应用 高频易错题集
试题解析
一.选择题(共10小题)
1.如图,五架轰炸机组成了一个三角形飞行编队,且每架飞机都在边长等于1正方形网格格点上,其中A、B两架轰炸机对应点的坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么轰炸机C对应点的坐标是( )
A.(2,﹣1) B.(4,﹣2) C.(4,2) D.(2,0)
解:因为A(﹣2,1)和B(﹣2,﹣3),
所以建立如图所示的坐标系,可得点C的坐标为(2,﹣1),
故选:A.
2.某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是( )
A.第3组第2排 B.第3组第1排 C.第2组第3排 D.第2组第2排
解:某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是第2组第3排,
故选:C.
3.已知点(3﹣2k2,4k﹣3)在第一象限的角平分线上,则k=( )
A.1 B.﹣1 C.0 D.0或1
解:∵点(3﹣2k2,4k﹣3)在第一象限的角平分线上,
∴3﹣2k2=4k﹣3,
整理得,k2+2k﹣3=0,
解得k1=﹣3,k2=1,
当k=﹣3时,3﹣2×(﹣3)2=﹣15,
点为(﹣15,﹣15),在第三象限,舍去;
当k=1时,3﹣2×12=1,
点为(1,1),在第一象限,
所以k=1.
故选:A.
4.已知点A(﹣1,﹣2)和点B(3,m﹣1),如果直线AB∥x轴,那么m的值为( )
A.1 B.﹣4 C.﹣1 D.3
解:∵点A(﹣1,﹣2)和点B(3,m﹣1),直线AB∥x轴,
∴﹣2=m﹣1,
∴m=﹣1,
故选:C.
5.对于直角坐标平面内的任意两点A(x1,y1),B(x2,y2),定义它们之间的一种“距离”:
||AB||=|x2﹣x1|+|y2﹣y1|.给出下列三个命题:
①若点C在线段AB上,则||AC||+||CB||=||AB||;
②在△ABC中,若∠C=90°,则||AC||2+||CB||2=||AB||2;
③在△ABC中,||AC||+||CB||>||AB||.其中真命题的个数为( )
A.0 B.1 C.2 D.3
解:对于直角坐标平面内的任意两点A(x1,y1),B(x2,y2),
定义它们之间的一种“距离”:||AB||=|x2﹣x1|+|y2﹣y1|.
对于①若点C在线段AB上,设C点坐标为(x0,y0),x0在x1、x2之间,y0在y1、y2之间,
则||AC||+||CB||=|x0﹣x1|+|y0﹣y1|+|x2﹣x0|+|y2﹣y0|=|x2﹣x1|+|y2﹣y1|=||AB||成立,故①正确.
对于②平方后不能消除x0,y0,命题不成立;
对于③在△ABC中,||AC||+||CB||=|x0﹣x1|+|y0﹣y1|+|x2﹣x0|+|y2﹣y0|≥|(x0﹣x1)+(x2﹣x0)|+|(y0﹣y1)+(y2﹣y0)|=|x2﹣x1|+|y2﹣y1|=||AB||.③不一定成立
∴命题①成立,
故选:B.
6.如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(﹣1,1),第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(﹣2,2),第四次向右跳动5个单位至点A4(3,2),…,以此规律跳动下去,点A第2020次跳动至点A2020的坐标是( )
A.(1012,1011) B.(1009,1008)
C.(1010,1009) D.(1011,1010)
解:因为A1(﹣1,1),A2(2,1)
A3(﹣2,2)A4(3,2)
A5(﹣3,3)A6(4,3)
A7(﹣4,4)A8(5,4)
…
A2n﹣1(﹣n,n) A2n(n+1,n)(n为正整数)
所以2n=2020,
n=1010
所以A2020(1011,1010)
故选:D.
7.将点P(2m+3,m﹣2)向上平移2个单位得到P′,且P′在x轴上,那么点P的坐标是( )
A.(3,﹣2) B.(3,0) C.(7,0) D.(9,1)
解:∵将点P(2m+3,m﹣2)向上平移2个单位得到P′,
∴P′的坐标为(2m+3,m),
∵P′在x轴上,
∴m=0,
∴点P的坐标是(3,﹣2).
故选:A.
8.将某图形的各顶点的横坐标保持不变,纵坐标减去3,可将该图形( )
A.横向向右平移3个单位 B.横向向左平移3个单位
C.纵向向上平移3个单位 D.纵向向下平移3个单位
解:∵某图形的各顶点的横坐标保持不变,纵坐标减去3,
∴将该图形向下平移了3个单位.
故选:D.
9.已知坐标平面内的点A(﹣2,4),如果将平面直角坐标系向左平移3个单位长度,再向上平移2个单位长度,那么平移后点A的坐标是( )
A.(1,6) B.(﹣5,6) C.(﹣5,2) D.(1,2)
解:∵坐标平面内点A(﹣2,4),将坐标系先向左平移3个单位长度,再向上平移2个单位长度,
∴点A的横坐标增大3,纵坐标减小2,
∴点A变化后的坐标为(1,2).
故选:D.
10.线段AB经过平移得到线段CD,其中点A、B的对应点分别为点C、D,这四个点都在如图所示的格点上,那么线段AB上的一点P(a,b)经过平移后,在线段CD上的对应点Q的坐标是( )
A.(a﹣1,b+3) B.(a﹣1,b﹣3) C.(a+1,b+3) D.(a+1,b﹣3)
解:由图可得,点A、B的对应点分别为点C、D,而B(1,3),D(2,0),
∴线段AB向右平移1个单位,向下平移3个单位得到线段CD,
又∵P(a,b),
∴Q(a+1,b﹣3),
故选:D.
二.填空题(共5小题)
11.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动一个单位,依次得到点P1(0,1);P2(1,1);P3(1,0);P4(1,﹣1);P5(2,﹣1);P6(2,0)……,则点P2019的坐标是 (673,0) .
解:由P3、P6、P9 可得规律:当下标为3的整数倍时,横坐标为,纵坐标为0,
∵2019÷3=673,
∴P2019 (673,0)
则点P2019的坐标是 (673,0).
故答案为 (673,0).
12.如图,在围棋盘上有三枚棋子,如果黑棋①的位置用坐标表为(0,﹣1),黑棋②的位置用坐标表示为(﹣3,0),则白棋③坐标表示为 (﹣4,2)
解:黑棋①的位置用坐标表为(0,﹣1),黑棋②的位置用坐标表示为(﹣3,0),可建立平面直角坐标系,如图,
∴白棋③的坐标为(﹣4,2).
故答案为:(﹣4,2).
13.平面直角坐标系中,已知点A(a,3),点B(2,b),若线段AB被y轴垂直平分,则a+b= 1 .
解:∵线段AB被y轴垂直平分,
∴点A(a,3)与点B(2,b)关于y轴对称,
∴a=﹣2,b=3,
∴a+b=﹣2+3=1.
故答案为:1.
14.将点P(﹣1,2)向左平移2个单位,再向上平移1个单位所得的对应点的坐标为 (﹣3,3) .
解:点P(﹣1,2)向左平移2个单位,再向上平移1个单位所得的对应点的坐标为(﹣1﹣2,2+1),即对应点的坐标是(﹣3,3).
故答案填:(﹣3,3).
15.已知点M(a﹣1,5),现在将平面直角坐标系先向左平移3个单位,之后又向下平移4个单位,得到点N(2,b﹣1),则a= 0 ,b= 10 .
解:由题意得a﹣1+3=2;5+4=b﹣1
解得a=0;b=10,
故答案为0;10.
三.解答题(共5小题)
16.如图所示,是一个围棋盘的平面示意图(每个小正方形边长为1个单位长度)
(1)已知白棋②的坐标为(﹣1,1),写出白棋④的坐标和黑棋的坐标;
(2)若白棋②的坐标为(3,1),则白棋④的坐标和黑棋的坐标是否发生改变?若改变,请写出坐标;若不改变,请说明理由.
解:(1)根据白棋②的坐标为(﹣1,1),如图所示,建立直角坐标系,则白棋④的坐标为(0,﹣3),黑棋的坐标为(3,﹣2);
(2)根据白棋②的坐标为(3,1),白棋④的坐标和黑棋的坐标发生改变,
如图所示,建立直角坐标系,则白棋④的坐标为(4,﹣3),黑棋的坐标为(7,﹣2);
17.如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周)
(1)写出点B的坐标( 4 , 5 );
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴距离为4个单位长度时,求点P移动的时间.
解:(1)点B的坐标(4,5),故答案为:4,5;
(2)当点P移动了4秒时,点P移动了4×2=8个单位长度,
∵C点的坐标为(0,5),∴OC=5,∴8﹣5=3,
∴此时,点P的位置在线段BC上,且CP=3,
如图所示,点P的坐标为BC边中点(3,5).
(3)当点P在OC上时,OP=4,
此时所用时间为4÷2=2(s);
当点P在AB上时,AP=4,BP=1,
∵A点的坐标为(4,0)∴OA=CB=4,
∵C点的坐标为(0,5)∴OC=5,OC+CB+BP=5+4+1=10,此时所用时间为
10÷2=5(s);
综上所述,当点P移动2秒或5秒时,点P到x轴的距离为4个单位长度.
18.先阅读下列一段文字,再解答问题
已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|
(1)已知点A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点间的距离;
(3)已知点A(0,6)B(﹣3,2),C(3,2),判断线段AB,BC,AC中哪两条是相等的?并说明理由.
解:(1)依据两点间的距离公式,可得AB==13;
(2)当点A,B在平行于y轴的直线上时,AB=|﹣1﹣5|=6;
(3)AB与AC相等.理由:
∵AB==5;
AC==5;
BC=|3﹣(﹣3)|=6.
∴AB=AC.
19.已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值;
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
解:
(1)1﹣a=﹣3,a=4.
(2)由a=4得:2a﹣12=2×4﹣12=﹣4,又点Q(x,y)位于第二象限,所以y>0;
取y=1,得点Q的坐标为(﹣4,1).
(3)因为点P(2a﹣12,1﹣a)位于第三象限,
所以,
解得:1<a<6.
因为点P的横、纵坐标都是整数,所以a=2或3或4或5;
当a=2时,1﹣a=﹣1,所以PQ>1;
当a=3时,1﹣a=﹣2,所以PQ>2;
当a=4时,1﹣a=﹣3,所以PQ>3;
当a=5时,1﹣a=﹣4,所以PQ>4.
20.如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线移动(即:沿着长方形移动一周).
(1)写出点B的坐标( 4,6 ).
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
解:(1)根据长方形的性质,可得AB与y轴平行,BC与x轴平行;
故B的坐标为(4,6);
故答案为:(4,6);
(2)根据题意,P的运动速度为每秒2个单位长度,
当点P移动了4秒时,则其运动了8个长度单位,
此时P的坐标为(4,4),位于AB上;
(3)根据题意,点P到x轴距离为5个单位长度时,有两种情况:
P在AB上时,P运动了4+5=9个长度单位,此时P运动了4.5秒;
P在OC上时,P运动了4+6+4+1=15个长度单位,此时P运动了=7.5秒.
_21?????????è?????(www.21cnjy.com)_
