5.1 相交线 高频易错题汇编(附解析)
文档属性
| 名称 | 5.1 相交线 高频易错题汇编(附解析) |  | |
| 格式 | doc | ||
| 文件大小 | 369.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 19:05:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
5.1 相交线 高频易错题集
一.选择题(共10小题)
1.下列说法:①若|a|=﹣b,|b|=b,则a=b=0;②若﹣a不是正数,则a为非负数;③|﹣a2|=(﹣a)2;④若+=0,则=﹣1;⑤平面内n条直线两两相交,最多个交点.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
2.在一个平面内,任意四条直线相交,交点的个数最多有( )
A.7个 B.6个 C.5个 D.4个
3.如图,直线a、b相交形成四个角,互为对顶角的是( )
A.∠l与∠2 B.∠2与∠3 C.∠3与∠4 D.∠2与∠4
4.如图,∠1与∠2构成对顶角的是( )
A. B.
C. D.
5.如图,直线AB、CD相交于点O,OE平分∠BOD,过点O作OF⊥OE,若∠AOC=42°,则∠BOF的度数为( )
A.48° B.52° C.64° D.69°
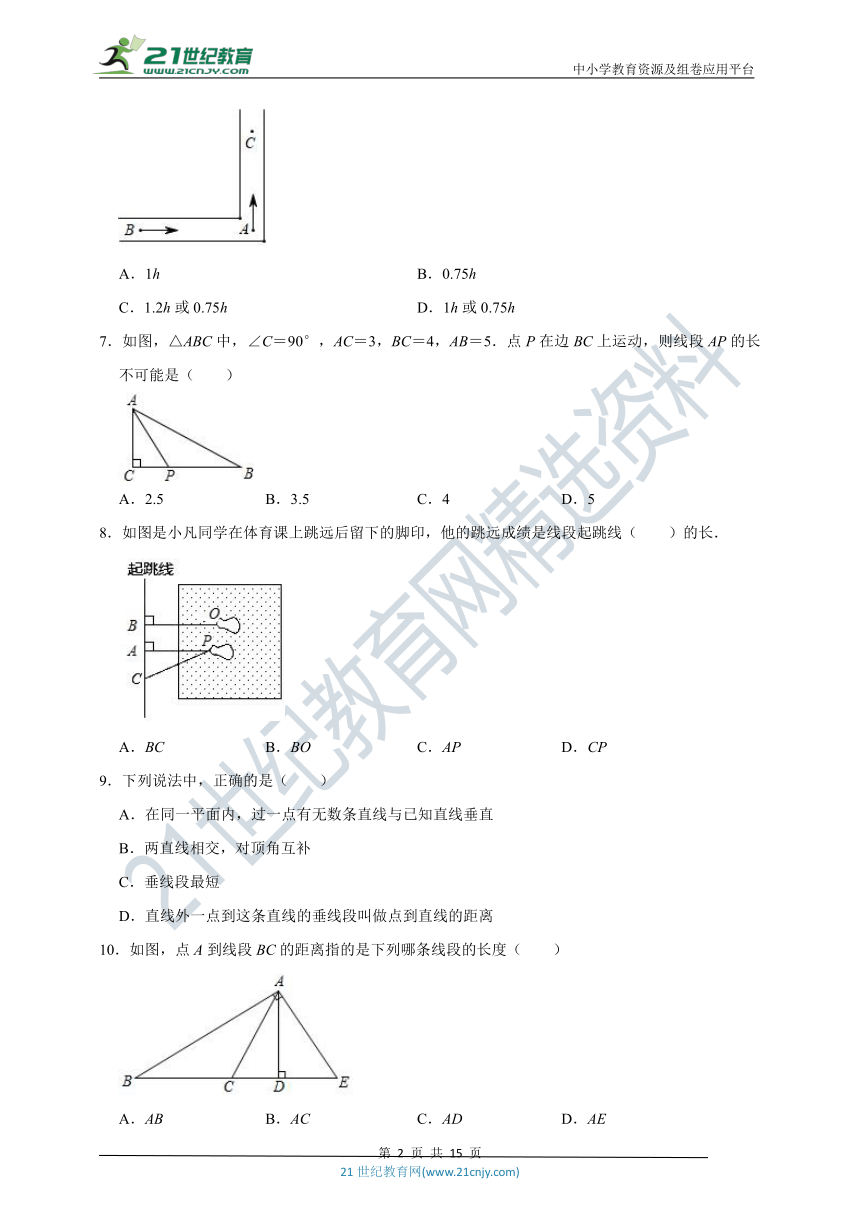
6.如图,是两条互相垂直的街道,且A到B,C的距离都是7km,现甲从B地走向A地,乙从A地走向C地,若两人同时出发且速度都是4km/h,则两人之间的距离为5km时,是甲出发后( )
A.1h B.0.75h
C.1.2h或0.75h D.1h或0.75h
7.如图,△ABC中,∠C=90°,AC=3,BC=4,AB=5.点P在边BC上运动,则线段AP的长不可能是( )
A.2.5 B.3.5 C.4 D.5
8.如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段起跳线( )的长.
A.BC B.BO C.AP D.CP
9.下列说法中,正确的是( )
A.在同一平面内,过一点有无数条直线与已知直线垂直
B.两直线相交,对顶角互补
C.垂线段最短
D.直线外一点到这条直线的垂线段叫做点到直线的距离
10.如图,点A到线段BC的距离指的是下列哪条线段的长度( )
A.AB B.AC C.AD D.AE
二.填空题(共5小题)
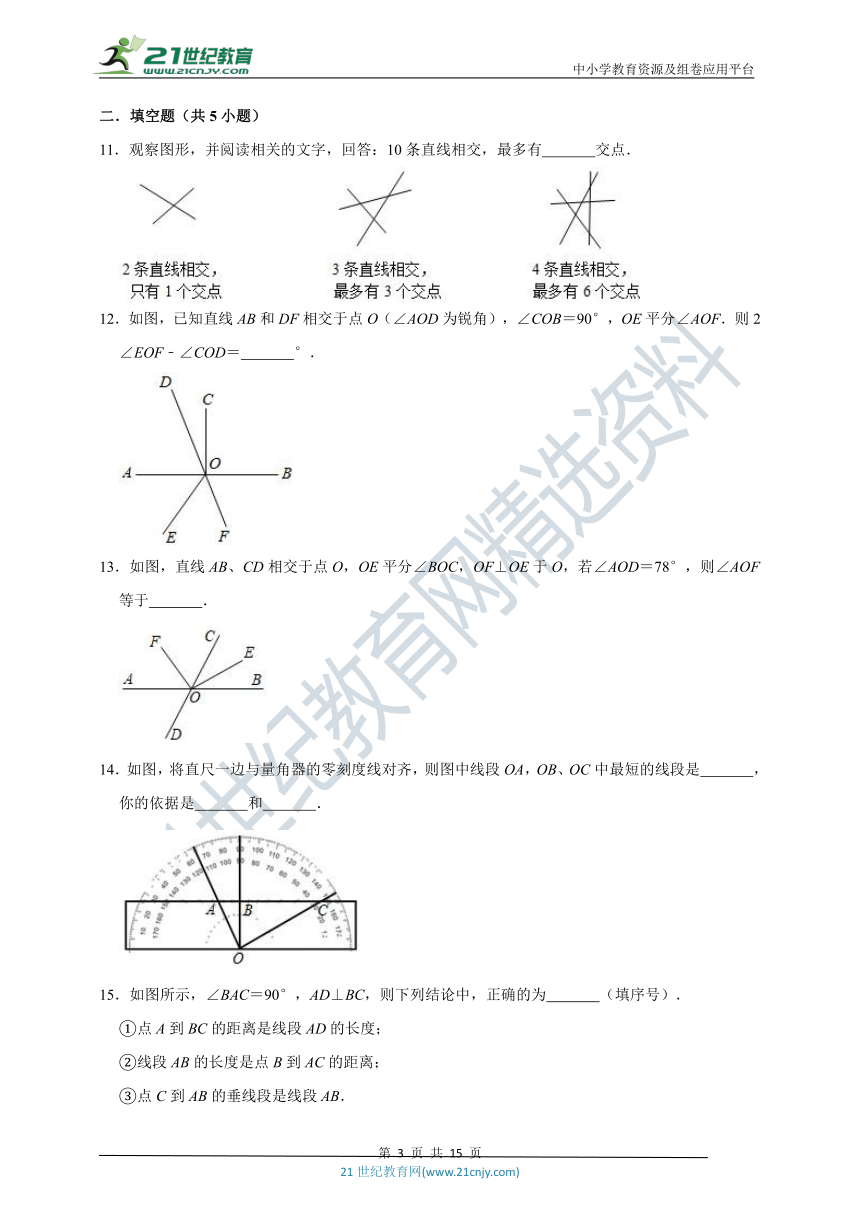
11.观察图形,并阅读相关的文字,回答:10条直线相交,最多有 交点.
12.如图,已知直线AB和DF相交于点O(∠AOD为锐角),∠COB=90°,OE平分∠AOF.则2∠EOF﹣∠COD= °.
13.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=78°,则∠AOF等于 .
14.如图,将直尺一边与量角器的零刻度线对齐,则图中线段OA,OB、OC中最短的线段是 ,你的依据是 和 .
15.如图所示,∠BAC=90°,AD⊥BC,则下列结论中,正确的为 (填序号).
①点A到BC的距离是线段AD的长度;
②线段AB的长度是点B到AC的距离;
③点C到AB的垂线段是线段AB.
三.解答题(共5小题)
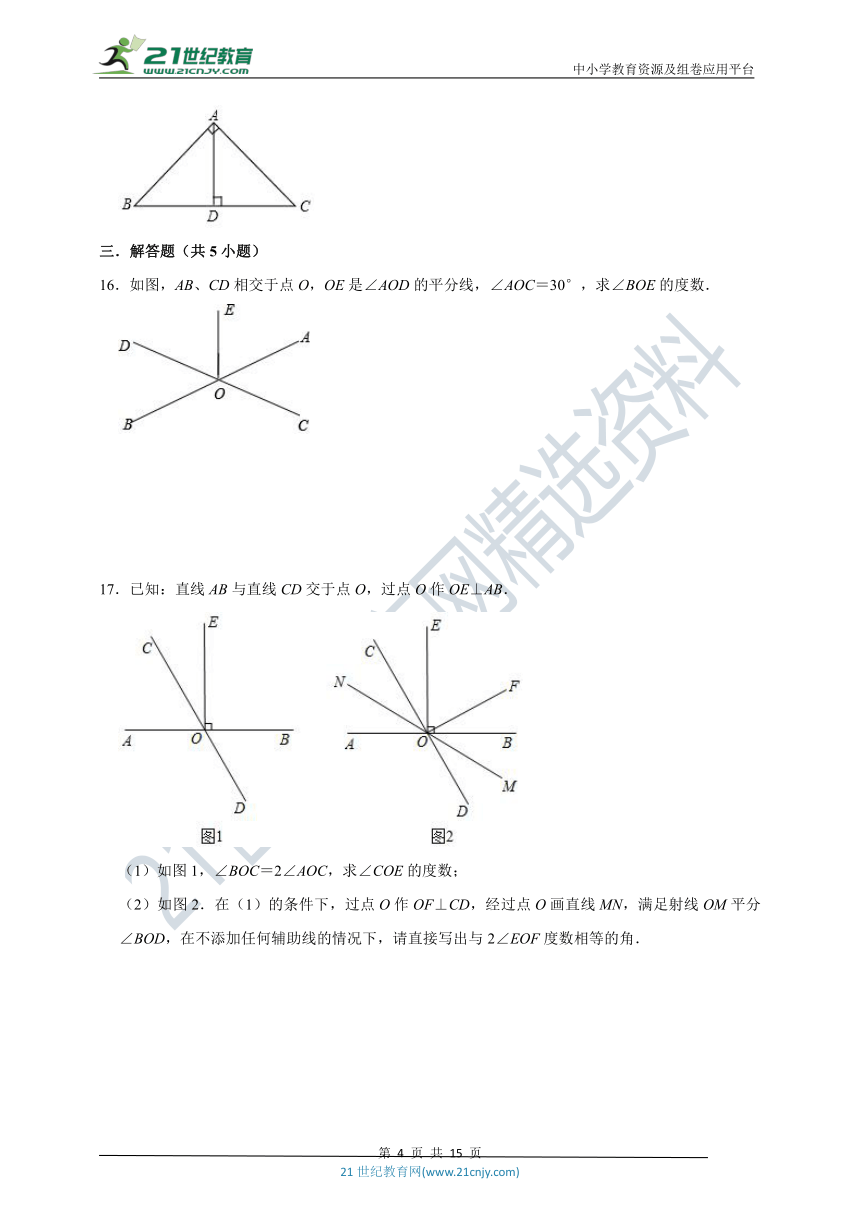
16.如图,AB、CD相交于点O,OE是∠AOD的平分线,∠AOC=30°,求∠BOE的度数.
17.已知:直线AB与直线CD交于点O,过点O作OE⊥AB.
(1)如图1,∠BOC=2∠AOC,求∠COE的度数;
(2)如图2.在(1)的条件下,过点O作OF⊥CD,经过点O画直线MN,满足射线OM平分∠BOD,在不添加任何辅助线的情况下,请直接写出与2∠EOF度数相等的角.
18.如图,要把河中的水引到水池A中,应在河岸B处开始挖渠才能使水渠的长度最短,请作出图形,并说明这样做依据的几何学原理.
19.操作:如图,直线AB与CD交于点O,按要求完成下列问题.
(1)用量角器量得∠AOC= 度.AB与CD的关系可记作 .
(2)画出∠BOC的角平分线OM,∠BOM=∠ = 度.
(3)在射线OM上取一点P,画出点P到直线AB的距离PE.
(4)如图若按“上北下南左西右东”的方位标记,请画出表示“南偏西30°”的射线OF.
20.如图所示,找出图中的同位角、内错角、同旁内角(仅限于用数字表示).
5.1 相交线 高频易错题集
试题解析
一.选择题(共10小题)
1.下列说法:①若|a|=﹣b,|b|=b,则a=b=0;②若﹣a不是正数,则a为非负数;③|﹣a2|=(﹣a)2;④若+=0,则=﹣1;⑤平面内n条直线两两相交,最多个交点.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
解:①若|a|=﹣b,|b|=b,则a=b=0,故本选项正确;
②若﹣a不是正数,则a为非负数,故本选项正确;
③|﹣a2|=(﹣a)2,故本选项正确;
④若+=0,则a,b异号,即=﹣1,故本选项正确;
⑤平面内n条直线两两相交,最多n(n﹣1)个交点,故本选项错误.
故选:C.
2.在一个平面内,任意四条直线相交,交点的个数最多有( )
A.7个 B.6个 C.5个 D.4个
解:如图所示:
①当4条直线经过同一个点时,
有1个交点;
②当3条直线经过同一个点,第4条不经过该点时,
有4个交点;
③当4条直线不经过同一点时,
有6个交点.
综上所述,4条直线相交最多有6个交点.
故选:B.
3.如图,直线a、b相交形成四个角,互为对顶角的是( )
A.∠l与∠2 B.∠2与∠3 C.∠3与∠4 D.∠2与∠4
解:由图可得,∠l与∠2,∠2与∠3,∠3与∠4都是邻补角;∠2与∠4,∠3与∠1都是对顶角,
故选:D.
4.如图,∠1与∠2构成对顶角的是( )
A. B.
C. D.
解:对顶角:∠1的两边与∠2的两边互为反向延长线,故C符合题意;
故选:C.
5.如图,直线AB、CD相交于点O,OE平分∠BOD,过点O作OF⊥OE,若∠AOC=42°,则∠BOF的度数为( )
A.48° B.52° C.64° D.69°
解:∵∠BOD=∠AOC(对顶角相等),∠AOC=42°(已知),
∴∠BOD=42°,
∵OE平分∠BOD(已知),
∴∠BOE=∠BOD=21°(角平分线的性质),
∵OF⊥OE(已知 ),
∴∠EOF=90°(垂直定义),
∵∠BOF+∠BOE=∠EOF,
∴∠BOF=∠EOF﹣∠BOE=90°﹣21°=69°,
∴∠BOF=69°.
故选:D.
6.如图,是两条互相垂直的街道,且A到B,C的距离都是7km,现甲从B地走向A地,乙从A地走向C地,若两人同时出发且速度都是4km/h,则两人之间的距离为5km时,是甲出发后( )
A.1h B.0.75h
C.1.2h或0.75h D.1h或0.75h
解:设甲出发后xh,两人之间的距离为5km时,
根据勾股定理,得
(7﹣4x)2+(4x)2=52,
32x2﹣56x+24=0,
解得:x=1或x=0.75,
故选:D.
7.如图,△ABC中,∠C=90°,AC=3,BC=4,AB=5.点P在边BC上运动,则线段AP的长不可能是( )
A.2.5 B.3.5 C.4 D.5
解:∵∠C=90°,点P在边BC上运动,
∴AB≥AP≥AC,
又∵AC=3,BC=4,AB=5,
∴AP的长不可能是2.5,
故选:A.
8.如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段起跳线( )的长.
A.BC B.BO C.AP D.CP
解:依据垂线段最短,他的跳远成绩是线段起跳线AP的长,
故选:C.
9.下列说法中,正确的是( )
A.在同一平面内,过一点有无数条直线与已知直线垂直
B.两直线相交,对顶角互补
C.垂线段最短
D.直线外一点到这条直线的垂线段叫做点到直线的距离
解:A.在同一平面内,过一点有且仅有一条直线与已知直线垂直,故本选项错误;
B.两直线相交,对顶角相等,故本选项错误;
C.垂线段最短,故本选项正确;
D.直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故本选项错误;
故选:C.
10.如图,点A到线段BC的距离指的是下列哪条线段的长度( )
A.AB B.AC C.AD D.AE
解:由图可得,AD⊥BC于D,点A到线段BC的距离指线段AD的长,
故选:C.
二.填空题(共5小题)
11.观察图形,并阅读相关的文字,回答:10条直线相交,最多有 45 交点.
解:∵10条直线两两相交:3条直线相交最多有3个交点,4条直线相交最多有6个交点,
5条直线相交最多有10个交点,而3=×2×3,6=×3×4,10=1+2+3+4=×4×5,
∴十条直线相交最多有交点的个数是:n(n﹣1)=×10×9=45.
故答案为:45.
12.如图,已知直线AB和DF相交于点O(∠AOD为锐角),∠COB=90°,OE平分∠AOF.则2∠EOF﹣∠COD= 90 °.
解:∵OE平分∠AOF,
∴∠AOF=2∠EOF,
∵∠AOF=∠BOD,∠COB=90°,
∴2∠EOF﹣∠COD=∠AOF﹣∠COD=∠BOD﹣∠COD=∠COB=90°.
故答案为:90.
13.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=78°,则∠AOF等于 51° .
解:∵∠BOC=∠AOD=78°,OE平分∠BOC,
∴∠BOE=∠BOC=39°.
∵OF⊥OE,
∴∠EOF=90°.
∴∠AOF=180°﹣∠EOF﹣∠BOE=180°﹣90°﹣39°=51°.
故答案为:51°.
14.如图,将直尺一边与量角器的零刻度线对齐,则图中线段OA,OB、OC中最短的线段是 OB ,你的依据是 垂线段最短 和 平行线的性质 .
解:由题可得,图中线段OA,OB、OC中最短的线段是OB,依据为垂线段最短和平行线的性质.
故答案为:OB,垂线段最短,平行线的性质.
15.如图所示,∠BAC=90°,AD⊥BC,则下列结论中,正确的为 ①② (填序号).
①点A到BC的距离是线段AD的长度;
②线段AB的长度是点B到AC的距离;
③点C到AB的垂线段是线段AB.
解:∵AD⊥BC,
∴点A到BC的距离是线段AD的长度,①正确;
∵∠BAC=90°,
∴AB⊥AC,
∴线段AB的长度是点B到AC的距离,②正确
∵AB⊥AC,
∴C到AB的垂线段是线段AC,③不正确.
其中正确的为①②,
故答案是:①②.
三.解答题(共5小题)
16.如图,AB、CD相交于点O,OE是∠AOD的平分线,∠AOC=30°,求∠BOE的度数.
解:∵∠AOC=30°,
∴∠AOD=180°﹣∠AOC=150°,
∵OE是∠AOD的平分线,
∴∠DOE=∠AOD=75°,
∵∠DOB=∠AOC=30°,
∴∠BOE=∠DOB+∠DOE=105°.
17.已知:直线AB与直线CD交于点O,过点O作OE⊥AB.
(1)如图1,∠BOC=2∠AOC,求∠COE的度数;
(2)如图2.在(1)的条件下,过点O作OF⊥CD,经过点O画直线MN,满足射线OM平分∠BOD,在不添加任何辅助线的情况下,请直接写出与2∠EOF度数相等的角.
解:(1)如图1,∵∠AOC+∠BOC=180°,且∠BOC=2∠AOC,
∴∠AOC=60°,
∵OE⊥AB,
∴∠AOE=90°,
∴∠COE=90°﹣60°=30°;
(2)如图2,由(1)知:∠AOC=60°,
∵射线OM平分∠BOD,
∴∠BOM=∠DOM=∠AON=∠CON=30°,
∵OE⊥AB,OC⊥OF,
∴∠AOE=∠COF=90°,
∴∠AOC=∠EOF=60°,
∴∠AOD=∠BOC=∠FON=∠EOM=180°﹣60°=120°=2∠EOF,
∴与2∠EOF度数相等的角是:∠AOD,∠BOC,∠FON,∠EOM.
18.如图,要把河中的水引到水池A中,应在河岸B处开始挖渠才能使水渠的长度最短,请作出图形,并说明这样做依据的几何学原理.
解:过点A作CD的垂线段AB,则AB的长度最短,依据为:垂线段最短,
19.操作:如图,直线AB与CD交于点O,按要求完成下列问题.
(1)用量角器量得∠AOC= 90 度.AB与CD的关系可记作 AB⊥CD .
(2)画出∠BOC的角平分线OM,∠BOM=∠ COM = 45 度.
(3)在射线OM上取一点P,画出点P到直线AB的距离PE.
(4)如图若按“上北下南左西右东”的方位标记,请画出表示“南偏西30°”的射线OF.
解:(1)用量角器量得∠AOC=90°,AB与CD的关系可记作 AB⊥CD,
故答案为:90,AB⊥CD;
(2)如图所示,OM即为所求,∠BOM=∠COM=45°,
故答案为:COM,45;
(3)如图所示,PE即为所求;
(4)如图所示,OF即为所求.
20.如图所示,找出图中的同位角、内错角、同旁内角(仅限于用数字表示).
解:由图可得:
同位角:∠1与∠3,∠3与∠5;
内错角:∠1与∠4,∠4与∠5;
同旁内角:∠1与∠2,∠6与∠5.
_21?????????è?????(www.21cnjy.com)_
5.1 相交线 高频易错题集
一.选择题(共10小题)
1.下列说法:①若|a|=﹣b,|b|=b,则a=b=0;②若﹣a不是正数,则a为非负数;③|﹣a2|=(﹣a)2;④若+=0,则=﹣1;⑤平面内n条直线两两相交,最多个交点.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
2.在一个平面内,任意四条直线相交,交点的个数最多有( )
A.7个 B.6个 C.5个 D.4个
3.如图,直线a、b相交形成四个角,互为对顶角的是( )
A.∠l与∠2 B.∠2与∠3 C.∠3与∠4 D.∠2与∠4
4.如图,∠1与∠2构成对顶角的是( )
A. B.
C. D.
5.如图,直线AB、CD相交于点O,OE平分∠BOD,过点O作OF⊥OE,若∠AOC=42°,则∠BOF的度数为( )
A.48° B.52° C.64° D.69°
6.如图,是两条互相垂直的街道,且A到B,C的距离都是7km,现甲从B地走向A地,乙从A地走向C地,若两人同时出发且速度都是4km/h,则两人之间的距离为5km时,是甲出发后( )
A.1h B.0.75h
C.1.2h或0.75h D.1h或0.75h
7.如图,△ABC中,∠C=90°,AC=3,BC=4,AB=5.点P在边BC上运动,则线段AP的长不可能是( )
A.2.5 B.3.5 C.4 D.5
8.如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段起跳线( )的长.
A.BC B.BO C.AP D.CP
9.下列说法中,正确的是( )
A.在同一平面内,过一点有无数条直线与已知直线垂直
B.两直线相交,对顶角互补
C.垂线段最短
D.直线外一点到这条直线的垂线段叫做点到直线的距离
10.如图,点A到线段BC的距离指的是下列哪条线段的长度( )
A.AB B.AC C.AD D.AE
二.填空题(共5小题)
11.观察图形,并阅读相关的文字,回答:10条直线相交,最多有 交点.
12.如图,已知直线AB和DF相交于点O(∠AOD为锐角),∠COB=90°,OE平分∠AOF.则2∠EOF﹣∠COD= °.
13.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=78°,则∠AOF等于 .
14.如图,将直尺一边与量角器的零刻度线对齐,则图中线段OA,OB、OC中最短的线段是 ,你的依据是 和 .
15.如图所示,∠BAC=90°,AD⊥BC,则下列结论中,正确的为 (填序号).
①点A到BC的距离是线段AD的长度;
②线段AB的长度是点B到AC的距离;
③点C到AB的垂线段是线段AB.
三.解答题(共5小题)
16.如图,AB、CD相交于点O,OE是∠AOD的平分线,∠AOC=30°,求∠BOE的度数.
17.已知:直线AB与直线CD交于点O,过点O作OE⊥AB.
(1)如图1,∠BOC=2∠AOC,求∠COE的度数;
(2)如图2.在(1)的条件下,过点O作OF⊥CD,经过点O画直线MN,满足射线OM平分∠BOD,在不添加任何辅助线的情况下,请直接写出与2∠EOF度数相等的角.
18.如图,要把河中的水引到水池A中,应在河岸B处开始挖渠才能使水渠的长度最短,请作出图形,并说明这样做依据的几何学原理.
19.操作:如图,直线AB与CD交于点O,按要求完成下列问题.
(1)用量角器量得∠AOC= 度.AB与CD的关系可记作 .
(2)画出∠BOC的角平分线OM,∠BOM=∠ = 度.
(3)在射线OM上取一点P,画出点P到直线AB的距离PE.
(4)如图若按“上北下南左西右东”的方位标记,请画出表示“南偏西30°”的射线OF.
20.如图所示,找出图中的同位角、内错角、同旁内角(仅限于用数字表示).
5.1 相交线 高频易错题集
试题解析
一.选择题(共10小题)
1.下列说法:①若|a|=﹣b,|b|=b,则a=b=0;②若﹣a不是正数,则a为非负数;③|﹣a2|=(﹣a)2;④若+=0,则=﹣1;⑤平面内n条直线两两相交,最多个交点.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
解:①若|a|=﹣b,|b|=b,则a=b=0,故本选项正确;
②若﹣a不是正数,则a为非负数,故本选项正确;
③|﹣a2|=(﹣a)2,故本选项正确;
④若+=0,则a,b异号,即=﹣1,故本选项正确;
⑤平面内n条直线两两相交,最多n(n﹣1)个交点,故本选项错误.
故选:C.
2.在一个平面内,任意四条直线相交,交点的个数最多有( )
A.7个 B.6个 C.5个 D.4个
解:如图所示:
①当4条直线经过同一个点时,
有1个交点;
②当3条直线经过同一个点,第4条不经过该点时,
有4个交点;
③当4条直线不经过同一点时,
有6个交点.
综上所述,4条直线相交最多有6个交点.
故选:B.
3.如图,直线a、b相交形成四个角,互为对顶角的是( )
A.∠l与∠2 B.∠2与∠3 C.∠3与∠4 D.∠2与∠4
解:由图可得,∠l与∠2,∠2与∠3,∠3与∠4都是邻补角;∠2与∠4,∠3与∠1都是对顶角,
故选:D.
4.如图,∠1与∠2构成对顶角的是( )
A. B.
C. D.
解:对顶角:∠1的两边与∠2的两边互为反向延长线,故C符合题意;
故选:C.
5.如图,直线AB、CD相交于点O,OE平分∠BOD,过点O作OF⊥OE,若∠AOC=42°,则∠BOF的度数为( )
A.48° B.52° C.64° D.69°
解:∵∠BOD=∠AOC(对顶角相等),∠AOC=42°(已知),
∴∠BOD=42°,
∵OE平分∠BOD(已知),
∴∠BOE=∠BOD=21°(角平分线的性质),
∵OF⊥OE(已知 ),
∴∠EOF=90°(垂直定义),
∵∠BOF+∠BOE=∠EOF,
∴∠BOF=∠EOF﹣∠BOE=90°﹣21°=69°,
∴∠BOF=69°.
故选:D.
6.如图,是两条互相垂直的街道,且A到B,C的距离都是7km,现甲从B地走向A地,乙从A地走向C地,若两人同时出发且速度都是4km/h,则两人之间的距离为5km时,是甲出发后( )
A.1h B.0.75h
C.1.2h或0.75h D.1h或0.75h
解:设甲出发后xh,两人之间的距离为5km时,
根据勾股定理,得
(7﹣4x)2+(4x)2=52,
32x2﹣56x+24=0,
解得:x=1或x=0.75,
故选:D.
7.如图,△ABC中,∠C=90°,AC=3,BC=4,AB=5.点P在边BC上运动,则线段AP的长不可能是( )
A.2.5 B.3.5 C.4 D.5
解:∵∠C=90°,点P在边BC上运动,
∴AB≥AP≥AC,
又∵AC=3,BC=4,AB=5,
∴AP的长不可能是2.5,
故选:A.
8.如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段起跳线( )的长.
A.BC B.BO C.AP D.CP
解:依据垂线段最短,他的跳远成绩是线段起跳线AP的长,
故选:C.
9.下列说法中,正确的是( )
A.在同一平面内,过一点有无数条直线与已知直线垂直
B.两直线相交,对顶角互补
C.垂线段最短
D.直线外一点到这条直线的垂线段叫做点到直线的距离
解:A.在同一平面内,过一点有且仅有一条直线与已知直线垂直,故本选项错误;
B.两直线相交,对顶角相等,故本选项错误;
C.垂线段最短,故本选项正确;
D.直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故本选项错误;
故选:C.
10.如图,点A到线段BC的距离指的是下列哪条线段的长度( )
A.AB B.AC C.AD D.AE
解:由图可得,AD⊥BC于D,点A到线段BC的距离指线段AD的长,
故选:C.
二.填空题(共5小题)
11.观察图形,并阅读相关的文字,回答:10条直线相交,最多有 45 交点.
解:∵10条直线两两相交:3条直线相交最多有3个交点,4条直线相交最多有6个交点,
5条直线相交最多有10个交点,而3=×2×3,6=×3×4,10=1+2+3+4=×4×5,
∴十条直线相交最多有交点的个数是:n(n﹣1)=×10×9=45.
故答案为:45.
12.如图,已知直线AB和DF相交于点O(∠AOD为锐角),∠COB=90°,OE平分∠AOF.则2∠EOF﹣∠COD= 90 °.
解:∵OE平分∠AOF,
∴∠AOF=2∠EOF,
∵∠AOF=∠BOD,∠COB=90°,
∴2∠EOF﹣∠COD=∠AOF﹣∠COD=∠BOD﹣∠COD=∠COB=90°.
故答案为:90.
13.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=78°,则∠AOF等于 51° .
解:∵∠BOC=∠AOD=78°,OE平分∠BOC,
∴∠BOE=∠BOC=39°.
∵OF⊥OE,
∴∠EOF=90°.
∴∠AOF=180°﹣∠EOF﹣∠BOE=180°﹣90°﹣39°=51°.
故答案为:51°.
14.如图,将直尺一边与量角器的零刻度线对齐,则图中线段OA,OB、OC中最短的线段是 OB ,你的依据是 垂线段最短 和 平行线的性质 .
解:由题可得,图中线段OA,OB、OC中最短的线段是OB,依据为垂线段最短和平行线的性质.
故答案为:OB,垂线段最短,平行线的性质.
15.如图所示,∠BAC=90°,AD⊥BC,则下列结论中,正确的为 ①② (填序号).
①点A到BC的距离是线段AD的长度;
②线段AB的长度是点B到AC的距离;
③点C到AB的垂线段是线段AB.
解:∵AD⊥BC,
∴点A到BC的距离是线段AD的长度,①正确;
∵∠BAC=90°,
∴AB⊥AC,
∴线段AB的长度是点B到AC的距离,②正确
∵AB⊥AC,
∴C到AB的垂线段是线段AC,③不正确.
其中正确的为①②,
故答案是:①②.
三.解答题(共5小题)
16.如图,AB、CD相交于点O,OE是∠AOD的平分线,∠AOC=30°,求∠BOE的度数.
解:∵∠AOC=30°,
∴∠AOD=180°﹣∠AOC=150°,
∵OE是∠AOD的平分线,
∴∠DOE=∠AOD=75°,
∵∠DOB=∠AOC=30°,
∴∠BOE=∠DOB+∠DOE=105°.
17.已知:直线AB与直线CD交于点O,过点O作OE⊥AB.
(1)如图1,∠BOC=2∠AOC,求∠COE的度数;
(2)如图2.在(1)的条件下,过点O作OF⊥CD,经过点O画直线MN,满足射线OM平分∠BOD,在不添加任何辅助线的情况下,请直接写出与2∠EOF度数相等的角.
解:(1)如图1,∵∠AOC+∠BOC=180°,且∠BOC=2∠AOC,
∴∠AOC=60°,
∵OE⊥AB,
∴∠AOE=90°,
∴∠COE=90°﹣60°=30°;
(2)如图2,由(1)知:∠AOC=60°,
∵射线OM平分∠BOD,
∴∠BOM=∠DOM=∠AON=∠CON=30°,
∵OE⊥AB,OC⊥OF,
∴∠AOE=∠COF=90°,
∴∠AOC=∠EOF=60°,
∴∠AOD=∠BOC=∠FON=∠EOM=180°﹣60°=120°=2∠EOF,
∴与2∠EOF度数相等的角是:∠AOD,∠BOC,∠FON,∠EOM.
18.如图,要把河中的水引到水池A中,应在河岸B处开始挖渠才能使水渠的长度最短,请作出图形,并说明这样做依据的几何学原理.
解:过点A作CD的垂线段AB,则AB的长度最短,依据为:垂线段最短,
19.操作:如图,直线AB与CD交于点O,按要求完成下列问题.
(1)用量角器量得∠AOC= 90 度.AB与CD的关系可记作 AB⊥CD .
(2)画出∠BOC的角平分线OM,∠BOM=∠ COM = 45 度.
(3)在射线OM上取一点P,画出点P到直线AB的距离PE.
(4)如图若按“上北下南左西右东”的方位标记,请画出表示“南偏西30°”的射线OF.
解:(1)用量角器量得∠AOC=90°,AB与CD的关系可记作 AB⊥CD,
故答案为:90,AB⊥CD;
(2)如图所示,OM即为所求,∠BOM=∠COM=45°,
故答案为:COM,45;
(3)如图所示,PE即为所求;
(4)如图所示,OF即为所求.
20.如图所示,找出图中的同位角、内错角、同旁内角(仅限于用数字表示).
解:由图可得:
同位角:∠1与∠3,∠3与∠5;
内错角:∠1与∠4,∠4与∠5;
同旁内角:∠1与∠2,∠6与∠5.
_21?????????è?????(www.21cnjy.com)_
