18.1 平行四边形 高频易错题汇编(含解析)
文档属性
| 名称 | 18.1 平行四边形 高频易错题汇编(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 418.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 18:59:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
18.1 平行四边形 高频易错题集
一.选择题(共10小题)
1.如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5cm,BC=3cm,那么平行线a,b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
2.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c的距离是( )
A.2cm B.8cm C.8或2cm D.不能确定
3.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,点E,G为垂足,则下列说法中错误的是( )
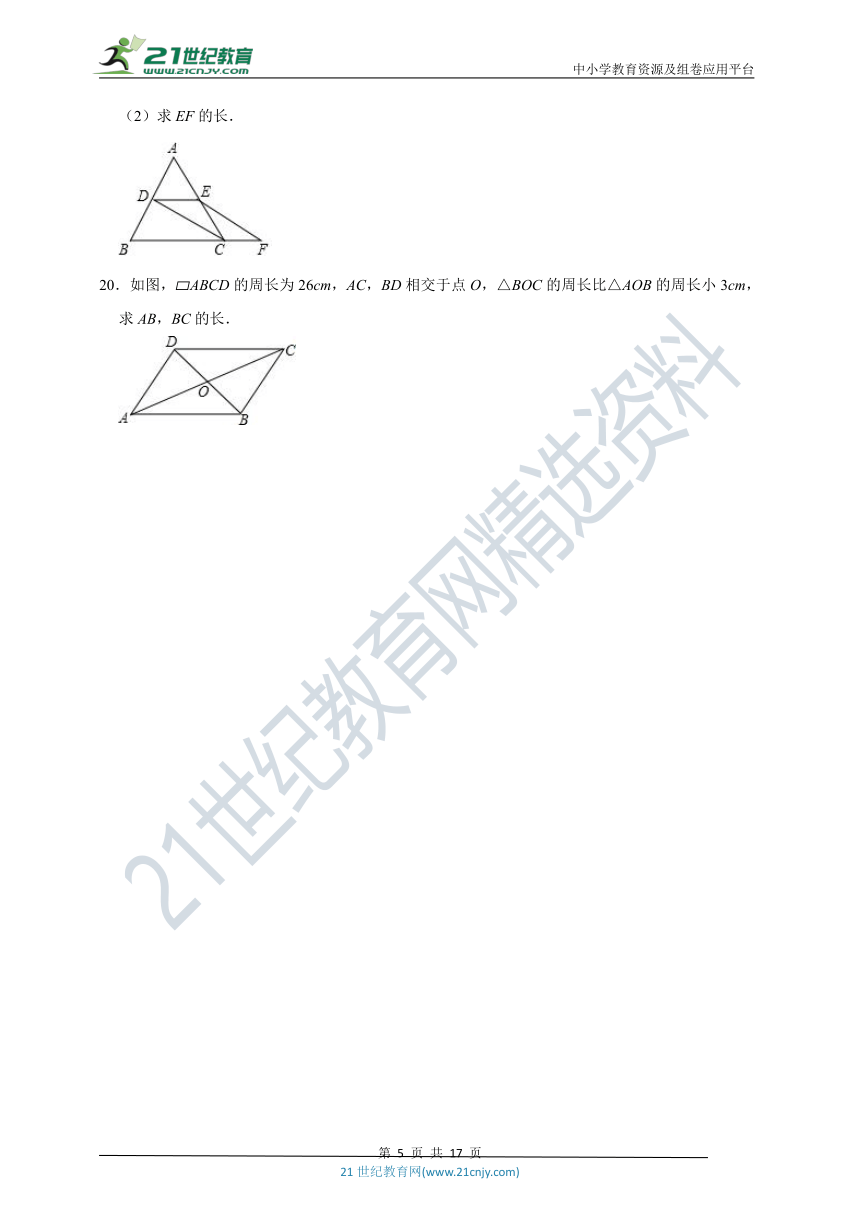
A.AB=CD
B.CE=FG
C.A,B两点之间的距离就是线段AB的长
D.直线a,b之间的距离就是线段CD的长
4.如图所示,a∥b,直线a与直线b之间的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段CD的长度
5.如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形,……如此操作下去,那么第5个三角形直角顶点的坐标为( )
A.(﹣,) B.(﹣)
C.(﹣) D.(﹣)
6.如图,在△ABC中,D,E分别是AB,AC的中点,AC=10,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为( )
A.10 B.12 C.14 D.16
7.如图,BC=6,D、E分别是线段AB和线段AC的中点,那么线段DE的长是( )
A.6 B.5 C.4.5 D.3
8.如图所示,已知△ABC的周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,…依此类推,第2006个三角形的周长为( )
A. B. C. D.
9.如图,在?ABCD中,AB=3,AD=5,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=( )
A.1 B. C.2 D.3
10.点A,B,C,D在同一平面内,从四个条件中(1)AB=CD,(2)AB∥CD,(3)BC=AD,(4)BC∥AD中任选两个,使四边形ABCD是平行四边形,这样的选法有( )
A.3种 B.4种 C.5种 D.6种
二.填空题(共5小题)
11.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 cm.
12.已知直线a∥b,点M到直线a的距离是4cm,到直线b的距离是2cm,那么直线a和直线b之间的距离为 .
13.如图,在四边形ABCD中,∠ADC+∠BCD=220°,E、F分别是AC、BD的中点,P是AB边上的中点,则∠EPF= °.
14.如图,△ABC中,AB=8,AC=6,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则EF为 .
15.如图,将平行四边形ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(8,0),点C的坐标是(2,6),则点B的坐标是 .
三.解答题(共5小题)
16.如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.
17.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.
18.如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于点F,E为BC的中点,求DE的长.
19.如图等边三角形ABC的边长为2,D、E分别为AB、AC的中点,延长BC至F,使CF=BC,连结CD和EF.
(1)求证:DE=CF
(2)求EF的长.
20.如图,?ABCD的周长为26cm,AC,BD相交于点O,△BOC的周长比△AOB的周长小3cm,求AB,BC的长.
试题解析
一.选择题(共10小题)
1.如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5cm,BC=3cm,那么平行线a,b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
解:∵AC⊥b,
∴△ABC是直角三角形,
∵AB=5cm,BC=3cm,
∴AC===4(cm),
∴平行线a、b之间的距离是:AC=4cm.
故选:B.
2.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c的距离是( )
A.2cm B.8cm C.8或2cm D.不能确定
解:有两种情况,如图:
(1)直线a与c的距离是3厘米+5厘米=8厘米;
(2)直线a与c的距离是5厘米﹣3厘米=2厘米;
故选:C.
3.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,点E,G为垂足,则下列说法中错误的是( )
A.AB=CD
B.CE=FG
C.A,B两点之间的距离就是线段AB的长
D.直线a,b之间的距离就是线段CD的长
解:A、∵CE⊥b,FG⊥b,∴FG∥EC,故此选项正确,不符合题意;
B、∵a∥b,FG∥EC,∴四边形FGEC是平行四边形,∴FG=EC,故此选项正确,不符合题意;
C、A、B两点的距离就是线段AB的长,此选项正确,不符合题意;
D、直线a、b间的距离就是线段CE的长,故此选项错误,符合题意.
故选:D.
4.如图所示,a∥b,直线a与直线b之间的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段CD的长度
解:由图可得,a∥b,AP⊥a,
∴直线a与直线b之间的距离是线段PA的长度,
故选:A.
5.如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形,……如此操作下去,那么第5个三角形直角顶点的坐标为( )
A.(﹣,) B.(﹣)
C.(﹣) D.(﹣)
解:由题意:第1个三角形的直角顶点坐标:(﹣2,2);
第2个三角形的直角顶点坐标:(﹣1,1);
第3个三角形的第1个三角形的直角顶点坐标:(﹣,);
第4个三角形的直角顶点坐标:(﹣,);
第5个三角形的直角顶点坐标:(﹣,);
故选:B.
6.如图,在△ABC中,D,E分别是AB,AC的中点,AC=10,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为( )
A.10 B.12 C.14 D.16
解:如图,∵∠AFC=90°,E是AC的中点,
∴Rt△ACF中,EF=AC==5,
∴DE=1+5=6;
∵D,E分别是AB,AC的中点,
∴DE为△ABC的中位线,
∴BC=2DE=12,
故选:B.
7.如图,BC=6,D、E分别是线段AB和线段AC的中点,那么线段DE的长是( )
A.6 B.5 C.4.5 D.3
解:如图,∵D、E分别是线段AB和线段AC的中点,
∴DE是△ABC的中位线,
∴DE=BC.
又BC=6,
∴DE=3.
故选:D.
8.如图所示,已知△ABC的周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,…依此类推,第2006个三角形的周长为( )
A. B. C. D.
解:△ABC的周长为1,新的三角形的三条边为△ABC的三条中位线,
根据中位线定理,三条中位线之和为三角形三条边的,
所以第2个三角形周长为;
第3个三角形的周长为;
以此类推,第N个三角形的周长为;
所以第2006个三角形的周长为.
故选:D.
9.如图,在?ABCD中,AB=3,AD=5,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=( )
A.1 B. C.2 D.3
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC=5,AB=CD=3,
∴∠ABE=∠CFE,
∵∠ABC的平分线交AD于点E,
∴∠ABE=∠CBF,
∴∠CBF=∠CFB,
∴CF=CB=5,
∴DF=CF﹣CD=5﹣3=2,
故选:C.
10.点A,B,C,D在同一平面内,从四个条件中(1)AB=CD,(2)AB∥CD,(3)BC=AD,(4)BC∥AD中任选两个,使四边形ABCD是平行四边形,这样的选法有( )
A.3种 B.4种 C.5种 D.6种
解:任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有(1)(2);(3)(4);(1)(3);(2)(4)共四种.
故选:B.
二.填空题(共5小题)
11.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 7或17 cm.
解:分两种情况:
①当EF在AB,CD之间时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12﹣5=7(cm).
②当AB,CD在EF同侧时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12+5=17(cm).
综上所述,EF与AB的距离为7cm或17cm.
故答案为:7或17.
12.已知直线a∥b,点M到直线a的距离是4cm,到直线b的距离是2cm,那么直线a和直线b之间的距离为 6cm或2cm .
解:分为两种情况:当M在a、b之间时,如在M′点时,直线a和直线b之间的距离是4cm+2cm=6cm;
当M在a、b外时,直线a和直线b之间的距离是4cm﹣2cm=2cm;
故答案为:6cm或2cm.
13.如图,在四边形ABCD中,∠ADC+∠BCD=220°,E、F分别是AC、BD的中点,P是AB边上的中点,则∠EPF= 40 °.
解:∵四边形ABCD中,∠ADC+∠BCD=220°,
∴∠BAD+∠ABC=360°﹣220°=140°,
∵E、F分别是AC、BD的中点,P是AB边上的中点,
∴PE是△ABC的中位线,PF是△ABD的中位线,
∴PE∥BC,PF∥AD,
∴∠BPF=∠BAD,∠APE=∠ABC,
∴∠APE+∠BPF=∠BAD+∠ABC=140°,
∴∠EPF=180°﹣140°=40°,
故答案为:40.
14.如图,△ABC中,AB=8,AC=6,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则EF为 1 .
解:∵AD平分∠ABC,CG⊥AD,∴∠GAF=∠CAF,∠AFG=∠AFC
在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA),
∴AG=AC=6,GF=CF,
则BG=AB﹣AG=8﹣6=2.
又∵BE=CE,
∴EF是△BCG的中位线,
∴EF=BG=1.
故答案为:1.
15.如图,将平行四边形ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(8,0),点C的坐标是(2,6),则点B的坐标是 (10,6) .
解:∵四边形ABCD是平行四边形,
∴OA=BC,OA∥BC,
∵A(8,0),
∴OA=BC=8,
∵C(2,6),
∴B(10,6),
故答案为:(10,6)
三.解答题(共5小题)
16.如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.
解:如图,过点A作AC⊥l2于点C,
∵直线l1∥l2,AC⊥l2,
∴∠DAC=90°,
∵∠DAB=135°,
∴∠BAC=∠DAB﹣∠DAC=45°,
∴∠ABC=45°,
∴∠BAC=∠ABC,
∴AC=BC,
在Rt△ABC中,AC2+BC2=AB2,
2AC2=502,
∴
∴两平行线l1和l2之间的距离为25.
17.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.
(1)证明:∵AB=AC,点D,E分别是边AB,AC的中点
∴BD=EC
∵点F,G,H分别为BE,DE,BC的中点
∴FG∥BD,GF=
FH∥EC,FH=
∴FG=FH;
(2)证明:由(1)FG∥BD
又∵∠A=90°
∴FG⊥AC
∵FH∥EC
∴FG⊥FH;
(3)解:延长FG交AC于点K,
∵FG∥BD,∠A=80°
∴∠FKC=∠A=80°
∵FH∥EC
∴∠GFH=180°﹣∠FKC=100°
18.如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于点F,E为BC的中点,求DE的长.
解:∵AD平分∠BAC,BD⊥AD,
∴AB=AF=6,BD=DF,
∴CF=AC﹣AF=4,
∵BD=DF,E为BC的中点,
∴DE=CF=2.
19.如图等边三角形ABC的边长为2,D、E分别为AB、AC的中点,延长BC至F,使CF=BC,连结CD和EF.
(1)求证:DE=CF
(2)求EF的长.
解:(1)证明:∵DE分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴,
又∵,
∴DE=CF;
(2)∵△ABC是等边三角形,D是AB的中点,
∴,CD⊥AB,
在Rt△BDC中,BD2+CD2=BC2,
即,
∴CD=3,
又∵DE是△ABC的中位线,
∴DE∥CF,
∵DE=CF,
∴四边形DCFE是平行四边形,
∴EF=CD=3.
20.如图,?ABCD的周长为26cm,AC,BD相交于点O,△BOC的周长比△AOB的周长小3cm,求AB,BC的长.
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,
∵△AOB的周长比△BOC的周长多3cm,
∴(OA+OB+AB)﹣(OB+OC+BC)=8cm,
即AB﹣BC=3cm,①
∵平行四边形ABCD的周长为26cm,
∴AB+BC=13cm,②
由①②得到:AB=8cm,BC=5cm.
_21?????????è?????(www.21cnjy.com)_
18.1 平行四边形 高频易错题集
一.选择题(共10小题)
1.如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5cm,BC=3cm,那么平行线a,b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
2.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c的距离是( )
A.2cm B.8cm C.8或2cm D.不能确定
3.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,点E,G为垂足,则下列说法中错误的是( )
A.AB=CD
B.CE=FG
C.A,B两点之间的距离就是线段AB的长
D.直线a,b之间的距离就是线段CD的长
4.如图所示,a∥b,直线a与直线b之间的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段CD的长度
5.如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形,……如此操作下去,那么第5个三角形直角顶点的坐标为( )
A.(﹣,) B.(﹣)
C.(﹣) D.(﹣)
6.如图,在△ABC中,D,E分别是AB,AC的中点,AC=10,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为( )
A.10 B.12 C.14 D.16
7.如图,BC=6,D、E分别是线段AB和线段AC的中点,那么线段DE的长是( )
A.6 B.5 C.4.5 D.3
8.如图所示,已知△ABC的周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,…依此类推,第2006个三角形的周长为( )
A. B. C. D.
9.如图,在?ABCD中,AB=3,AD=5,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=( )
A.1 B. C.2 D.3
10.点A,B,C,D在同一平面内,从四个条件中(1)AB=CD,(2)AB∥CD,(3)BC=AD,(4)BC∥AD中任选两个,使四边形ABCD是平行四边形,这样的选法有( )
A.3种 B.4种 C.5种 D.6种
二.填空题(共5小题)
11.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 cm.
12.已知直线a∥b,点M到直线a的距离是4cm,到直线b的距离是2cm,那么直线a和直线b之间的距离为 .
13.如图,在四边形ABCD中,∠ADC+∠BCD=220°,E、F分别是AC、BD的中点,P是AB边上的中点,则∠EPF= °.
14.如图,△ABC中,AB=8,AC=6,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则EF为 .
15.如图,将平行四边形ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(8,0),点C的坐标是(2,6),则点B的坐标是 .
三.解答题(共5小题)
16.如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.
17.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.
18.如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于点F,E为BC的中点,求DE的长.
19.如图等边三角形ABC的边长为2,D、E分别为AB、AC的中点,延长BC至F,使CF=BC,连结CD和EF.
(1)求证:DE=CF
(2)求EF的长.
20.如图,?ABCD的周长为26cm,AC,BD相交于点O,△BOC的周长比△AOB的周长小3cm,求AB,BC的长.
试题解析
一.选择题(共10小题)
1.如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5cm,BC=3cm,那么平行线a,b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
解:∵AC⊥b,
∴△ABC是直角三角形,
∵AB=5cm,BC=3cm,
∴AC===4(cm),
∴平行线a、b之间的距离是:AC=4cm.
故选:B.
2.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c的距离是( )
A.2cm B.8cm C.8或2cm D.不能确定
解:有两种情况,如图:
(1)直线a与c的距离是3厘米+5厘米=8厘米;
(2)直线a与c的距离是5厘米﹣3厘米=2厘米;
故选:C.
3.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,点E,G为垂足,则下列说法中错误的是( )
A.AB=CD
B.CE=FG
C.A,B两点之间的距离就是线段AB的长
D.直线a,b之间的距离就是线段CD的长
解:A、∵CE⊥b,FG⊥b,∴FG∥EC,故此选项正确,不符合题意;
B、∵a∥b,FG∥EC,∴四边形FGEC是平行四边形,∴FG=EC,故此选项正确,不符合题意;
C、A、B两点的距离就是线段AB的长,此选项正确,不符合题意;
D、直线a、b间的距离就是线段CE的长,故此选项错误,符合题意.
故选:D.
4.如图所示,a∥b,直线a与直线b之间的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段CD的长度
解:由图可得,a∥b,AP⊥a,
∴直线a与直线b之间的距离是线段PA的长度,
故选:A.
5.如图,将腰长为4的等腰直角三角形放在直角坐标系中,顺次连接各边中点得到第1个三角形,再顺次连接各边中点得到第2个三角形,……如此操作下去,那么第5个三角形直角顶点的坐标为( )
A.(﹣,) B.(﹣)
C.(﹣) D.(﹣)
解:由题意:第1个三角形的直角顶点坐标:(﹣2,2);
第2个三角形的直角顶点坐标:(﹣1,1);
第3个三角形的第1个三角形的直角顶点坐标:(﹣,);
第4个三角形的直角顶点坐标:(﹣,);
第5个三角形的直角顶点坐标:(﹣,);
故选:B.
6.如图,在△ABC中,D,E分别是AB,AC的中点,AC=10,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为( )
A.10 B.12 C.14 D.16
解:如图,∵∠AFC=90°,E是AC的中点,
∴Rt△ACF中,EF=AC==5,
∴DE=1+5=6;
∵D,E分别是AB,AC的中点,
∴DE为△ABC的中位线,
∴BC=2DE=12,
故选:B.
7.如图,BC=6,D、E分别是线段AB和线段AC的中点,那么线段DE的长是( )
A.6 B.5 C.4.5 D.3
解:如图,∵D、E分别是线段AB和线段AC的中点,
∴DE是△ABC的中位线,
∴DE=BC.
又BC=6,
∴DE=3.
故选:D.
8.如图所示,已知△ABC的周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,…依此类推,第2006个三角形的周长为( )
A. B. C. D.
解:△ABC的周长为1,新的三角形的三条边为△ABC的三条中位线,
根据中位线定理,三条中位线之和为三角形三条边的,
所以第2个三角形周长为;
第3个三角形的周长为;
以此类推,第N个三角形的周长为;
所以第2006个三角形的周长为.
故选:D.
9.如图,在?ABCD中,AB=3,AD=5,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=( )
A.1 B. C.2 D.3
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC=5,AB=CD=3,
∴∠ABE=∠CFE,
∵∠ABC的平分线交AD于点E,
∴∠ABE=∠CBF,
∴∠CBF=∠CFB,
∴CF=CB=5,
∴DF=CF﹣CD=5﹣3=2,
故选:C.
10.点A,B,C,D在同一平面内,从四个条件中(1)AB=CD,(2)AB∥CD,(3)BC=AD,(4)BC∥AD中任选两个,使四边形ABCD是平行四边形,这样的选法有( )
A.3种 B.4种 C.5种 D.6种
解:任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有(1)(2);(3)(4);(1)(3);(2)(4)共四种.
故选:B.
二.填空题(共5小题)
11.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 7或17 cm.
解:分两种情况:
①当EF在AB,CD之间时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12﹣5=7(cm).
②当AB,CD在EF同侧时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12+5=17(cm).
综上所述,EF与AB的距离为7cm或17cm.
故答案为:7或17.
12.已知直线a∥b,点M到直线a的距离是4cm,到直线b的距离是2cm,那么直线a和直线b之间的距离为 6cm或2cm .
解:分为两种情况:当M在a、b之间时,如在M′点时,直线a和直线b之间的距离是4cm+2cm=6cm;
当M在a、b外时,直线a和直线b之间的距离是4cm﹣2cm=2cm;
故答案为:6cm或2cm.
13.如图,在四边形ABCD中,∠ADC+∠BCD=220°,E、F分别是AC、BD的中点,P是AB边上的中点,则∠EPF= 40 °.
解:∵四边形ABCD中,∠ADC+∠BCD=220°,
∴∠BAD+∠ABC=360°﹣220°=140°,
∵E、F分别是AC、BD的中点,P是AB边上的中点,
∴PE是△ABC的中位线,PF是△ABD的中位线,
∴PE∥BC,PF∥AD,
∴∠BPF=∠BAD,∠APE=∠ABC,
∴∠APE+∠BPF=∠BAD+∠ABC=140°,
∴∠EPF=180°﹣140°=40°,
故答案为:40.
14.如图,△ABC中,AB=8,AC=6,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则EF为 1 .
解:∵AD平分∠ABC,CG⊥AD,∴∠GAF=∠CAF,∠AFG=∠AFC
在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA),
∴AG=AC=6,GF=CF,
则BG=AB﹣AG=8﹣6=2.
又∵BE=CE,
∴EF是△BCG的中位线,
∴EF=BG=1.
故答案为:1.
15.如图,将平行四边形ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(8,0),点C的坐标是(2,6),则点B的坐标是 (10,6) .
解:∵四边形ABCD是平行四边形,
∴OA=BC,OA∥BC,
∵A(8,0),
∴OA=BC=8,
∵C(2,6),
∴B(10,6),
故答案为:(10,6)
三.解答题(共5小题)
16.如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.
解:如图,过点A作AC⊥l2于点C,
∵直线l1∥l2,AC⊥l2,
∴∠DAC=90°,
∵∠DAB=135°,
∴∠BAC=∠DAB﹣∠DAC=45°,
∴∠ABC=45°,
∴∠BAC=∠ABC,
∴AC=BC,
在Rt△ABC中,AC2+BC2=AB2,
2AC2=502,
∴
∴两平行线l1和l2之间的距离为25.
17.如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.
(1)证明:∵AB=AC,点D,E分别是边AB,AC的中点
∴BD=EC
∵点F,G,H分别为BE,DE,BC的中点
∴FG∥BD,GF=
FH∥EC,FH=
∴FG=FH;
(2)证明:由(1)FG∥BD
又∵∠A=90°
∴FG⊥AC
∵FH∥EC
∴FG⊥FH;
(3)解:延长FG交AC于点K,
∵FG∥BD,∠A=80°
∴∠FKC=∠A=80°
∵FH∥EC
∴∠GFH=180°﹣∠FKC=100°
18.如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于点F,E为BC的中点,求DE的长.
解:∵AD平分∠BAC,BD⊥AD,
∴AB=AF=6,BD=DF,
∴CF=AC﹣AF=4,
∵BD=DF,E为BC的中点,
∴DE=CF=2.
19.如图等边三角形ABC的边长为2,D、E分别为AB、AC的中点,延长BC至F,使CF=BC,连结CD和EF.
(1)求证:DE=CF
(2)求EF的长.
解:(1)证明:∵DE分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴,
又∵,
∴DE=CF;
(2)∵△ABC是等边三角形,D是AB的中点,
∴,CD⊥AB,
在Rt△BDC中,BD2+CD2=BC2,
即,
∴CD=3,
又∵DE是△ABC的中位线,
∴DE∥CF,
∵DE=CF,
∴四边形DCFE是平行四边形,
∴EF=CD=3.
20.如图,?ABCD的周长为26cm,AC,BD相交于点O,△BOC的周长比△AOB的周长小3cm,求AB,BC的长.
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,
∵△AOB的周长比△BOC的周长多3cm,
∴(OA+OB+AB)﹣(OB+OC+BC)=8cm,
即AB﹣BC=3cm,①
∵平行四边形ABCD的周长为26cm,
∴AB+BC=13cm,②
由①②得到:AB=8cm,BC=5cm.
_21?????????è?????(www.21cnjy.com)_
