人教版七年级数学 下册 第九章 9.1.1 不等式及其解集 课件(共46张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第九章 9.1.1 不等式及其解集 课件(共46张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-03 22:57:34 | ||
图片预览











文档简介
(共46张PPT)
1.含有“=”的式子叫做等式;
2.
使等式两边相等的x的值称为方程的解;
3.
求方程的解的过程叫做解方程.
等式与方程
温故知新
谁长谁短
谁快谁慢
谁重谁轻
谁赢谁输
导入新课
这些,能用等式表示吗?
9.1.1
不等式及其解集
人教版七年级数学
下册
目标导航
1.了解不等式及其解的概念。
2.学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想。
3.理解不等式的解集及解不等式的意义。
认真阅读课本中9.1.1
不等式及其解集的内容,完成下面练习并体验知识点的形成过程。
自主研学
两个体重相同的孩子正在跷跷板上做游戏.现在换了一个小胖子上去,跷跷板发生了倾斜,游戏无法继续进行下去了.
这是什么原因呢?
两边不平衡了,也就是两边质量不相等了.
目标导学一:不等式的概念
合作交流
问题
一辆轿车在一条规定车速应高于60km/h,且低于100
km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km)与行驶时间x(h)之间的关系呢?
根据路程与速度、时间之间的关系可得:
s>60x,且s<100x.
观察由上述问题得到的关系式:x>1
,
x<100,x>50,s>60x,s<100x
,它们有什么共同的特点?
一般地,用不等号“>”,“<”连接而成的式子叫做不等式.像a≠2这样的式子也叫做不等式.
左右不相等
知识归纳
思考:下列式子有什么区别?
?
?
?
?
?
?
区别:
①只有(4)的式子里含有“=”符号;
②除了(4)的式子里含有“>”或“<”或“≥”或“≤”或“≠”符号;
代数式:
用运算符号(加、减、乘、除、乘方、开方)把数和表示数的字母连接而成的式子。例如:6,b,8a,
6b+3ac.
等式:
用“
=
”把代数式连接,表示相等关系的式子。
例如:5+3=8,2x=6,a=b,x-9=2.
知识回忆
不等式的定义:
用不等号(>,<,≥,≤,≠)连接而成的式子叫作不等式.
例如:156>155,155<156,x>50,s≥60x,s≤100x
符号“≥”读作“
”,也可读作“
”;
符号“≤”读作“
”,也可读作“
”;
符号“≠”读作“
”.
大于或等于
不小于
小于或等于
不大于
不等于
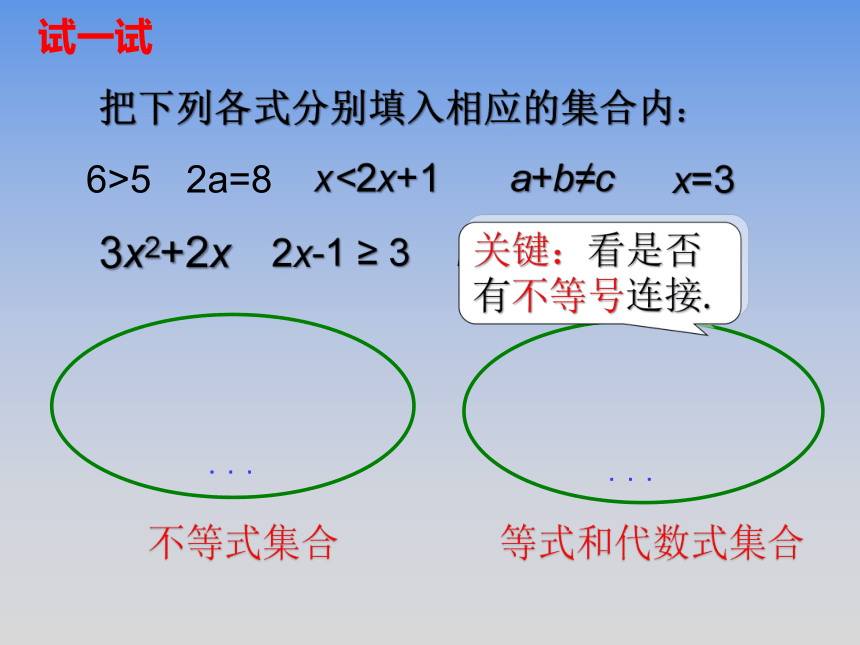
把下列各式分别填入相应的集合内:
...
...
不等式集合
等式和代数式集合
6>5
2a=8
x<2x+1
a+b≠c
x=3
3x2+2x
2x-1
≥
3
m-n<5
关键:看是否有不等号连接.
试一试
例1:判断下列式子是不是不等式:
①
-1<3
②
-x+2=4
③
3x
≠
4y
④
6
>
2
⑤
2x
-3
⑥
2m
<
n
是
不是
是
是
不是
是
探究:用不等式表示下列数量关系.
(1)x
的5倍大于-7;
(2)a
与
b
的和的一半小于-1;
(3)长、宽分别为xcm,
ycm
的长方形的面积小于边长为acm
的正方形的面积.
(1)关键词“大于”可以转化为符号_____;
(2)关键词“小于”可以转化为符号_____;
(3)长方形面积为_____,正方形面积为_____;关键词“小于”可以转化为符号____.
>
<
xycm2
a2cm2
<
(1)
5x>-7;
(2)
0.5
(a+b)<-1;
(3)
xy.
注意:在表示数量关系时,一定要注意“大于”、“小于”、“不小于”等关键性词语.
目标导学二:用不等式表示数量关系
例2
已知一支圆珠笔x元,签字笔与圆珠笔相比每支贵y元.
小华想要买3支圆珠笔和10支签字笔,若付50元仍找回若干元,则如何用含x,y的不等式来表示小华所需支付的金额与50元之间的关系?
解
3x+10(x+y)<50
关键词语
①大
于
②比…大
①小
于
②比…小
①不大于
②不超过
③至
多
①不小于
②不低于
③至
少
正数
负数
非正数
非负数
不等号
第一类:明确表明数量的不等关系
第二类:明确表明数量的范围特征
>
<
≤
≥
>0
<0
≤0
≥0
列不等式表示不等关系的步骤:先审题,分清数量的大小关系;找到关键词,选准不等号;再列出相应的代数式,用表示不等关系的符号列出不等式。
知识归纳
1.用不等式表示:
(1)a是正数;
(2)a是负数;
(3)
a与5的和小于7;
(4)a与2的差大于-1;
(5)a的4倍大于8;
(6)a的一半小于3.
解:
(1)a>0;
(2)a<0;
(3)a+5<7;
(4)a-2>-1;
(5)4a>8;
(6)
a<3.
即学即练
2.奥运射箭比赛,每一箭满分为10分.
某选手在参加比赛时,前十箭中最低得分为7分,求该选手前十箭总得分x的范围.
解:
即学即练
对于方程:
使等式两边相等的x的值称为方程的解.
对于不等式,不等式的解又是什么呢?
目标导学三:不等式的解与解集
问题:以下各数中哪些是不等式
的解?
76,73,79,80,74.9,75.1,90,60.
你能找出这个不等式其他的解吗?它到底有多少个解?你从中发现了什么规律?
√
×
√
√
×
√
√
×
当x>75时,不等式
成立;当x<75或x=75时,不等式
不成立.这就是说,任何大于75的数都是不等式
的解,这样的解有无数个.
分析归纳
我们曾经学过“使方程两边相等的未知数的值就是方程的解”,与方程类似
,
能使不等式成立的未知数的值叫不等式的解.
代入法是检验某个值是否是不等式的解的简单、实用的方法.
例如:100是x>50的解.
知识归纳
?
?
?
?
∴使不等式成立的80,78等就是不等式的解;
使不等式不成立的75,72就不是不等式的解;
?
代入法是检验某个值是否是不等式的解的简单实用的方法.
?
x
...
74
74.6
75
75.1
75.6
76
...
...
...
...
...
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
0
75
一般的,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
想一想:
1.不等式的解和不等式的解集是一样的吗?
2.不等式的解与解不等式一样吗?
求不等式的解集的过程叫解不等式.
知识归纳
不等式的解
不等式的解集
区别
定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中
的一员
解集一定包括了
某个解
不等式的解与不等式的解集的区别与联系
合作探究
(?
?
?
?)
(?
?
?
?)
(?
?
?
?)
即学即练
例4:直接想出不等式的解集:
⑴
x+2>6
⑵
3x>9
⑶
x-3>0
解:
⑴
x>4
;
⑵
x>3
;
⑶
x>3.
目标导学四:在数轴上表示不等式的解集
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2
因此可以像图那样表示不等式的解集x>2.
如何在数轴上表示出不等式x>2的解集呢?
0
1
2
3
4
5
6
-1
A
把表示2
的点A
画成空心圆圈,表示解集不包括2.
解集的表示方法:
第一种:用式子(如x>2),即用最简形式的不等式
(如x>a或x第二种:用数轴,一般标出数轴上某一区间,其中的
点对应的数值都是不等式的解.
画一画:
利用数轴来表示下列不等式的解集.
(1)x>-1
;
(2)
x<
.
0
-1
0
1
变式:
已知x的解集在数轴上表示如图,你能写出x的
解集吗?
0
-2
x<-2
表示-1的点
表示
的点
方向向右
方向向左
空心圆圈表示不含此点
1.
步骤:
①画数轴;
②定边界点;
③定方向.
2.
规律:
①大于向右画,小于向左画;
②有等号(≥
,≤)画实心点;
③无等号(>,<)画空心圆.
用数轴表示不等式的解集
不等式
x+1≥-1的解集为:
x
≥
-2
定方向
画数轴?
?
定点
例5:直接写出x+4<6的解集,并在数轴上表示出来.
0
1
2
解:x<2.
这个解集可以在数轴上表示为:
解:(1)x<-4;
(2)x>4.
0
-4
0
4
(1)
(2)
变式1:已知x的解集如图所示,你能写出x的解集吗?
变式2:直接写出不等式2x>8的解集,并在数轴上表示出来.
解:x>4.
这个解集在数轴上表示为:
0
4
变式3:直接写出不等式-2x>8的解集.
解:x<-4.
请直接想出下列不等式的解集,并在数轴上表示.
(1)
2x<8
(2)x-2>0
解:(1)不等式的解集为:
x<4
在数轴上表示如下:
○
4
0
解:(1)不等式的解集为:
x>2
在数轴上表示如下:
○
2
0
即学即练
1.不等式:
用符号“>”或“<”表示大小关系的式子.
2.不等式的解:
能使不等式成立的未知数的值.
4.解不等式:
求不等式的解集的过程.
3.不等式的解集:
使不等式成立的未知数的取值范围.
5.解集表示方式:
①不等式;
②数轴.
课堂小结
其中不等式有(?
?
?
?)
B
检测目标
下列式子哪些是不等式?哪些不是不等式?
答案:①②③⑤⑦⑧是不等式,④⑥不是.
检测目标
实数a,b在数轴上的位置关系如图所示,选择适当的不等号填空:
(3)a+b_____0
(1)a_____b
(2)
ab_____0
<
<
<
检测目标
在数轴上表示x≥-2正确的是
(
)
●
0
-2
B
-2
A
●
○
0
-2
C
●
0
-2
D
D
检测目标
不等式x<5有多少个解?有多少个正整数解?
解:不等式x<5有无数个解;
有4个正整数解,分别是4,3,2,1。
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
1.含有“=”的式子叫做等式;
2.
使等式两边相等的x的值称为方程的解;
3.
求方程的解的过程叫做解方程.
等式与方程
温故知新
谁长谁短
谁快谁慢
谁重谁轻
谁赢谁输
导入新课
这些,能用等式表示吗?
9.1.1
不等式及其解集
人教版七年级数学
下册
目标导航
1.了解不等式及其解的概念。
2.学会并准确运用不等式表示数量关系,形成在表达中渗透数形结合的思想。
3.理解不等式的解集及解不等式的意义。
认真阅读课本中9.1.1
不等式及其解集的内容,完成下面练习并体验知识点的形成过程。
自主研学
两个体重相同的孩子正在跷跷板上做游戏.现在换了一个小胖子上去,跷跷板发生了倾斜,游戏无法继续进行下去了.
这是什么原因呢?
两边不平衡了,也就是两边质量不相等了.
目标导学一:不等式的概念
合作交流
问题
一辆轿车在一条规定车速应高于60km/h,且低于100
km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km)与行驶时间x(h)之间的关系呢?
根据路程与速度、时间之间的关系可得:
s>60x,且s<100x.
观察由上述问题得到的关系式:x>1
,
x<100,x>50,s>60x,s<100x
,它们有什么共同的特点?
一般地,用不等号“>”,“<”连接而成的式子叫做不等式.像a≠2这样的式子也叫做不等式.
左右不相等
知识归纳
思考:下列式子有什么区别?
?
?
?
?
?
?
区别:
①只有(4)的式子里含有“=”符号;
②除了(4)的式子里含有“>”或“<”或“≥”或“≤”或“≠”符号;
代数式:
用运算符号(加、减、乘、除、乘方、开方)把数和表示数的字母连接而成的式子。例如:6,b,8a,
6b+3ac.
等式:
用“
=
”把代数式连接,表示相等关系的式子。
例如:5+3=8,2x=6,a=b,x-9=2.
知识回忆
不等式的定义:
用不等号(>,<,≥,≤,≠)连接而成的式子叫作不等式.
例如:156>155,155<156,x>50,s≥60x,s≤100x
符号“≥”读作“
”,也可读作“
”;
符号“≤”读作“
”,也可读作“
”;
符号“≠”读作“
”.
大于或等于
不小于
小于或等于
不大于
不等于
把下列各式分别填入相应的集合内:
...
...
不等式集合
等式和代数式集合
6>5
2a=8
x<2x+1
a+b≠c
x=3
3x2+2x
2x-1
≥
3
m-n<5
关键:看是否有不等号连接.
试一试
例1:判断下列式子是不是不等式:
①
-1<3
②
-x+2=4
③
3x
≠
4y
④
6
>
2
⑤
2x
-3
⑥
2m
<
n
是
不是
是
是
不是
是
探究:用不等式表示下列数量关系.
(1)x
的5倍大于-7;
(2)a
与
b
的和的一半小于-1;
(3)长、宽分别为xcm,
ycm
的长方形的面积小于边长为acm
的正方形的面积.
(1)关键词“大于”可以转化为符号_____;
(2)关键词“小于”可以转化为符号_____;
(3)长方形面积为_____,正方形面积为_____;关键词“小于”可以转化为符号____.
>
<
xycm2
a2cm2
<
(1)
5x>-7;
(2)
0.5
(a+b)<-1;
(3)
xy
注意:在表示数量关系时,一定要注意“大于”、“小于”、“不小于”等关键性词语.
目标导学二:用不等式表示数量关系
例2
已知一支圆珠笔x元,签字笔与圆珠笔相比每支贵y元.
小华想要买3支圆珠笔和10支签字笔,若付50元仍找回若干元,则如何用含x,y的不等式来表示小华所需支付的金额与50元之间的关系?
解
3x+10(x+y)<50
关键词语
①大
于
②比…大
①小
于
②比…小
①不大于
②不超过
③至
多
①不小于
②不低于
③至
少
正数
负数
非正数
非负数
不等号
第一类:明确表明数量的不等关系
第二类:明确表明数量的范围特征
>
<
≤
≥
>0
<0
≤0
≥0
列不等式表示不等关系的步骤:先审题,分清数量的大小关系;找到关键词,选准不等号;再列出相应的代数式,用表示不等关系的符号列出不等式。
知识归纳
1.用不等式表示:
(1)a是正数;
(2)a是负数;
(3)
a与5的和小于7;
(4)a与2的差大于-1;
(5)a的4倍大于8;
(6)a的一半小于3.
解:
(1)a>0;
(2)a<0;
(3)a+5<7;
(4)a-2>-1;
(5)4a>8;
(6)
a<3.
即学即练
2.奥运射箭比赛,每一箭满分为10分.
某选手在参加比赛时,前十箭中最低得分为7分,求该选手前十箭总得分x的范围.
解:
即学即练
对于方程:
使等式两边相等的x的值称为方程的解.
对于不等式,不等式的解又是什么呢?
目标导学三:不等式的解与解集
问题:以下各数中哪些是不等式
的解?
76,73,79,80,74.9,75.1,90,60.
你能找出这个不等式其他的解吗?它到底有多少个解?你从中发现了什么规律?
√
×
√
√
×
√
√
×
当x>75时,不等式
成立;当x<75或x=75时,不等式
不成立.这就是说,任何大于75的数都是不等式
的解,这样的解有无数个.
分析归纳
我们曾经学过“使方程两边相等的未知数的值就是方程的解”,与方程类似
,
能使不等式成立的未知数的值叫不等式的解.
代入法是检验某个值是否是不等式的解的简单、实用的方法.
例如:100是x>50的解.
知识归纳
?
?
?
?
∴使不等式成立的80,78等就是不等式的解;
使不等式不成立的75,72就不是不等式的解;
?
代入法是检验某个值是否是不等式的解的简单实用的方法.
?
x
...
74
74.6
75
75.1
75.6
76
...
...
...
...
...
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
0
75
一般的,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
想一想:
1.不等式的解和不等式的解集是一样的吗?
2.不等式的解与解不等式一样吗?
求不等式的解集的过程叫解不等式.
知识归纳
不等式的解
不等式的解集
区别
定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中
的一员
解集一定包括了
某个解
不等式的解与不等式的解集的区别与联系
合作探究
(?
?
?
?)
(?
?
?
?)
(?
?
?
?)
即学即练
例4:直接想出不等式的解集:
⑴
x+2>6
⑵
3x>9
⑶
x-3>0
解:
⑴
x>4
;
⑵
x>3
;
⑶
x>3.
目标导学四:在数轴上表示不等式的解集
先在数轴上标出表示2的点A
则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2
因此可以像图那样表示不等式的解集x>2.
如何在数轴上表示出不等式x>2的解集呢?
0
1
2
3
4
5
6
-1
A
把表示2
的点A
画成空心圆圈,表示解集不包括2.
解集的表示方法:
第一种:用式子(如x>2),即用最简形式的不等式
(如x>a或x
点对应的数值都是不等式的解.
画一画:
利用数轴来表示下列不等式的解集.
(1)x>-1
;
(2)
x<
.
0
-1
0
1
变式:
已知x的解集在数轴上表示如图,你能写出x的
解集吗?
0
-2
x<-2
表示-1的点
表示
的点
方向向右
方向向左
空心圆圈表示不含此点
1.
步骤:
①画数轴;
②定边界点;
③定方向.
2.
规律:
①大于向右画,小于向左画;
②有等号(≥
,≤)画实心点;
③无等号(>,<)画空心圆.
用数轴表示不等式的解集
不等式
x+1≥-1的解集为:
x
≥
-2
定方向
画数轴?
?
定点
例5:直接写出x+4<6的解集,并在数轴上表示出来.
0
1
2
解:x<2.
这个解集可以在数轴上表示为:
解:(1)x<-4;
(2)x>4.
0
-4
0
4
(1)
(2)
变式1:已知x的解集如图所示,你能写出x的解集吗?
变式2:直接写出不等式2x>8的解集,并在数轴上表示出来.
解:x>4.
这个解集在数轴上表示为:
0
4
变式3:直接写出不等式-2x>8的解集.
解:x<-4.
请直接想出下列不等式的解集,并在数轴上表示.
(1)
2x<8
(2)x-2>0
解:(1)不等式的解集为:
x<4
在数轴上表示如下:
○
4
0
解:(1)不等式的解集为:
x>2
在数轴上表示如下:
○
2
0
即学即练
1.不等式:
用符号“>”或“<”表示大小关系的式子.
2.不等式的解:
能使不等式成立的未知数的值.
4.解不等式:
求不等式的解集的过程.
3.不等式的解集:
使不等式成立的未知数的取值范围.
5.解集表示方式:
①不等式;
②数轴.
课堂小结
其中不等式有(?
?
?
?)
B
检测目标
下列式子哪些是不等式?哪些不是不等式?
答案:①②③⑤⑦⑧是不等式,④⑥不是.
检测目标
实数a,b在数轴上的位置关系如图所示,选择适当的不等号填空:
(3)a+b_____0
(1)a_____b
(2)
ab_____0
<
<
<
检测目标
在数轴上表示x≥-2正确的是
(
)
●
0
-2
B
-2
A
●
○
0
-2
C
●
0
-2
D
D
检测目标
不等式x<5有多少个解?有多少个正整数解?
解:不等式x<5有无数个解;
有4个正整数解,分别是4,3,2,1。
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
