人教版八年级数学下册 19.1 .1《变量与函数》同步习题(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学下册 19.1 .1《变量与函数》同步习题(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 777.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 17:32:39 | ||
图片预览



文档简介
19.1 .1 《变量与函数》同步习题
一、 选择题
1. 在某个变化过程中,数值保持不变的量,叫做( )
A.函数 B.变量 C.常量 D.自变量
2. 在关系式中,当自变量时,因变量的值为(????????)
A. B. C. D.
3. 以固定的速度向上抛出一个小球,小球的高度与小球运动的时间之间的关系式是=,在这个关系式中,常量、变量分别为???????
A.常量为,变量为, B.常量为,变量为,
C.常量为,,变量为, D.常量为,变量为,,
4. 已知函数,当自变量增加时,相应的函数值将增加( )
A. B. C. D.
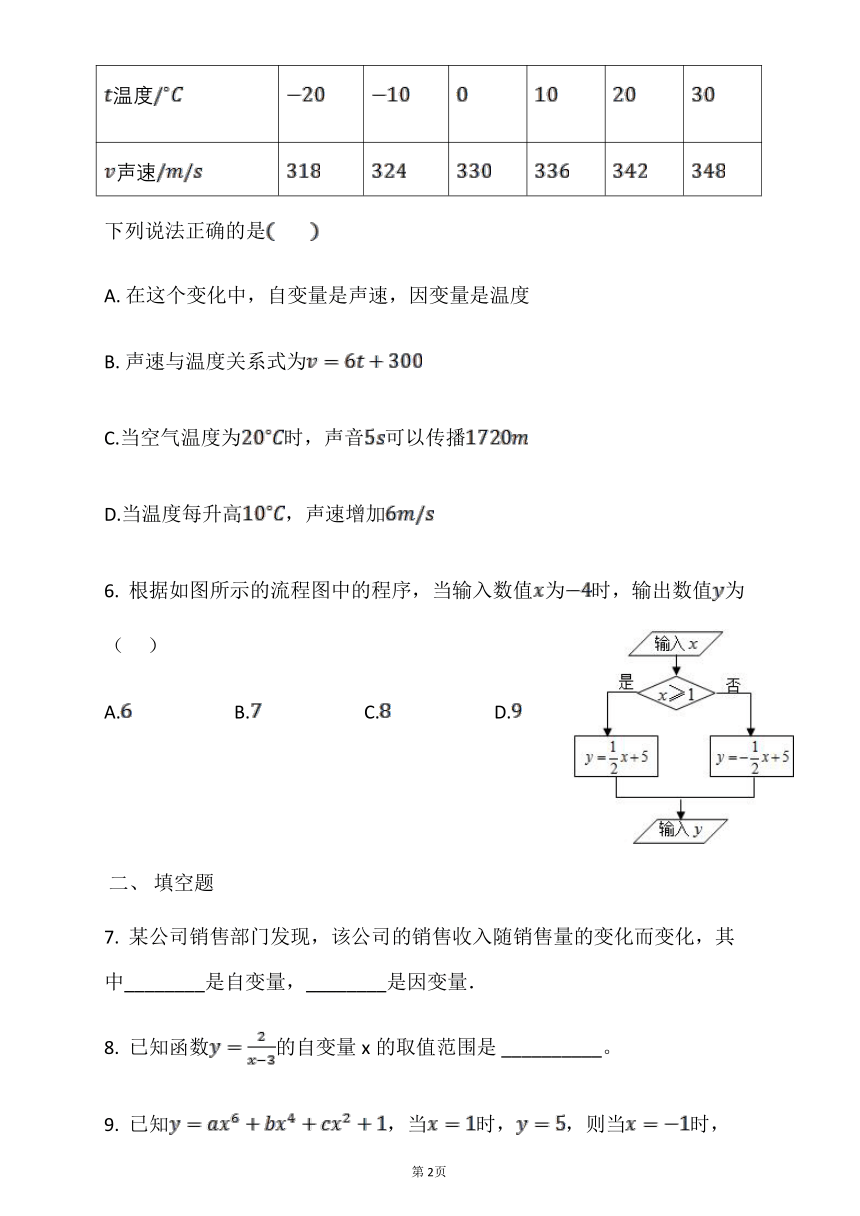
5. 某研学小组疫情期间在网上获取了声音在空气中传播的速度与空气温度之间关系的一些数据(如下表):
温度
声速
下列说法正确的是? ? ? ?
A. 在这个变化中,自变量是声速,因变量是温度
B. 声速与温度关系式为
C.当空气温度为时,声音可以传播
D.当温度每升高,声速增加
6. 根据如图所示的流程图中的程序,当输入数值为时,输出数值为( )
A. B. C. D.
二、 填空题?
7. 某公司销售部门发现,该公司的销售收入随销售量的变化而变化,其中________是自变量,________是因变量.
8. 已知函数的自变量x的取值范围是 __________。
9. 已知,当时,,则当时,________.
10. 已知函数 当时,,则当时,________.
11. 某商品原价为元,随着不同幅度的降价,日销量(单位:件)发生相应的变化(如下表).
这个表反映了两个变量之间的关系,________是自变量,________是因变量.从表中可以看出每降价元,日销量增加________件,从而可以估计降价之前的日销量为________件;如果售价为元时,日销量为_____件.
12. 已知函数,将此函数记作,其含义是指自变量取值时,对应的函数值为,如,,请计算________.
三、 解答题
13. 一辆汽车的油箱中现有汽油.如果不再加油,那么油箱中的余油量(单位:)随行驶里程(单位:)的增加而减少,平均每千米的耗油量为.
(1)写出与之间的函数关系式;
(2)写出自变量的取值范围;
(3)汽车行驶时,油箱中还有多少油?
(4)汽车最多可行驶多少千米?
?
14. 在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下面是测得的弹簧的长度与所挂物体的质量的一组对应值:
所挂物体的重量
弹簧长度
在这个变化的过程中,自变量是________;因变量是________;
写出与之间的关系式,并求出当所挂重物为时,弹簧的长度为多少?
参考答案与试题解析
19.1 .1《变量与函数》
一、 选择题
1.【答案】C
2.【答案】C
3.【答案】C
4.【答案】B
5.【答案】D
6.【答案】B
二、 填空题
7.【答案】销售量,销售收入
8.【答案】
9.【答案】
10.【答案】
11.【答案】降价金额,日销量,,,
12.【答案】
三、 解答题
13.【答案】
根据题意,每行程,耗油,即总油量减少,
则油箱中的油剩下,
∴ 与的函数关系式为:=;
因为代表的实际意义为行驶里程,所以不能为负数,即;
又行驶中的耗油量为,不能超过油箱中现有汽油量的值,
即,
解得,.
综上所述,自变量的取值范围是;
当=时,代入,的关系式:
==.
所以,汽车行驶时,油桶中还有汽油;
当=时,=,
解得=,
所以汽车最多可行驶千米.
14.【答案】
所挂物体的质量,弹簧长度
根据表格可知:所挂重物每增加千克,弹簧增长,
根据弹簧的长度弹簧原来的长度弹簧伸长的长度可知当所挂物体的重量为千克时,
弹簧长度,
将代入得.
所以当所挂重物为时,弹簧的长度为.
第4 44页
试卷第5 55页,总6 66页
一、 选择题
1. 在某个变化过程中,数值保持不变的量,叫做( )
A.函数 B.变量 C.常量 D.自变量
2. 在关系式中,当自变量时,因变量的值为(????????)
A. B. C. D.
3. 以固定的速度向上抛出一个小球,小球的高度与小球运动的时间之间的关系式是=,在这个关系式中,常量、变量分别为???????
A.常量为,变量为, B.常量为,变量为,
C.常量为,,变量为, D.常量为,变量为,,
4. 已知函数,当自变量增加时,相应的函数值将增加( )
A. B. C. D.
5. 某研学小组疫情期间在网上获取了声音在空气中传播的速度与空气温度之间关系的一些数据(如下表):
温度
声速
下列说法正确的是? ? ? ?
A. 在这个变化中,自变量是声速,因变量是温度
B. 声速与温度关系式为
C.当空气温度为时,声音可以传播
D.当温度每升高,声速增加
6. 根据如图所示的流程图中的程序,当输入数值为时,输出数值为( )
A. B. C. D.
二、 填空题?
7. 某公司销售部门发现,该公司的销售收入随销售量的变化而变化,其中________是自变量,________是因变量.
8. 已知函数的自变量x的取值范围是 __________。
9. 已知,当时,,则当时,________.
10. 已知函数 当时,,则当时,________.
11. 某商品原价为元,随着不同幅度的降价,日销量(单位:件)发生相应的变化(如下表).
这个表反映了两个变量之间的关系,________是自变量,________是因变量.从表中可以看出每降价元,日销量增加________件,从而可以估计降价之前的日销量为________件;如果售价为元时,日销量为_____件.
12. 已知函数,将此函数记作,其含义是指自变量取值时,对应的函数值为,如,,请计算________.
三、 解答题
13. 一辆汽车的油箱中现有汽油.如果不再加油,那么油箱中的余油量(单位:)随行驶里程(单位:)的增加而减少,平均每千米的耗油量为.
(1)写出与之间的函数关系式;
(2)写出自变量的取值范围;
(3)汽车行驶时,油箱中还有多少油?
(4)汽车最多可行驶多少千米?
?
14. 在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下面是测得的弹簧的长度与所挂物体的质量的一组对应值:
所挂物体的重量
弹簧长度
在这个变化的过程中,自变量是________;因变量是________;
写出与之间的关系式,并求出当所挂重物为时,弹簧的长度为多少?
参考答案与试题解析
19.1 .1《变量与函数》
一、 选择题
1.【答案】C
2.【答案】C
3.【答案】C
4.【答案】B
5.【答案】D
6.【答案】B
二、 填空题
7.【答案】销售量,销售收入
8.【答案】
9.【答案】
10.【答案】
11.【答案】降价金额,日销量,,,
12.【答案】
三、 解答题
13.【答案】
根据题意,每行程,耗油,即总油量减少,
则油箱中的油剩下,
∴ 与的函数关系式为:=;
因为代表的实际意义为行驶里程,所以不能为负数,即;
又行驶中的耗油量为,不能超过油箱中现有汽油量的值,
即,
解得,.
综上所述,自变量的取值范围是;
当=时,代入,的关系式:
==.
所以,汽车行驶时,油桶中还有汽油;
当=时,=,
解得=,
所以汽车最多可行驶千米.
14.【答案】
所挂物体的质量,弹簧长度
根据表格可知:所挂重物每增加千克,弹簧增长,
根据弹簧的长度弹簧原来的长度弹簧伸长的长度可知当所挂物体的重量为千克时,
弹簧长度,
将代入得.
所以当所挂重物为时,弹簧的长度为.
第4 44页
试卷第5 55页,总6 66页
