2021浙教版 九年级上册第3章复习学案 第八讲 能量转化的量度、简单的机械(含答案)
文档属性
| 名称 | 2021浙教版 九年级上册第3章复习学案 第八讲 能量转化的量度、简单的机械(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 235.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2021-02-04 10:40:10 | ||
图片预览



文档简介
浙江版 九年级上册科学学案
第八讲 能量转化的量度、简单的机械
3-3 能量转化的量度
1功
定义:如果一个力作用在物体上,且物体在这个力的方向上通过了一段距离,就说这个力对物体做了功。
力对物体做功的两个必要因素: 一是作用在物体上的力,二是物体在这个力的方向上通过了距离。
力不做功的三种情况
三种情况
原因
实例
有距离无力
物体没有受到力的作用,但由于惯性通过了一段距离,就是没有力做功。
足球离开脚后在水平面上滚动了一段距离,人对足球没有做功。
有力无距离
有力作用在物体上,但物体没有动,即物体没有通过距离。
两名同学没有搬起石头,所以对石头没有做功。
力与距离垂直
物体受到力的作用,也移动了一段距离,但通过的距离与力的方向垂直。
提着水桶水平移动了一段距离,竖直提水桶的力不做功
2功的计算
功的计算:功等于力与物体在力的方向上通过的距离的乘积。
公式:用F表示力,s表示力的方向上通过的距离,W表示功,则W=Fs。
单位:在国际单位制中,力的单位是牛,距离的单位是米,的单位是焦耳,简称焦(J)。
1 J = 1N X 1 m=1N??m。
应用W=Fs计算功时,力与物体通过的距离方向必须一致,且对应同一物体,同一段间。
3做功的实质
做功的过程实质就是能量转化的过程,力对物体做了多少功,就有多少能量发生了转化,因此,可以用功来量度能量转化的多少,能量的单位与功的单位一样,也是焦耳。
4功率
定义:功与做功所用的时间之比叫功率,它在数值上等于单位时间内所做的功。
物理意义:功率表示物体做功快慢的物理量。
公式:如果用P表示功率,用W表示功,用t表示做功所用的时间,功率的计算公式为
P=W/t。
单位:在国际单位制中,功的单位是焦,时间的单位是秒,功率的单位是焦耳每秒(J/s),他有一个专门的名称叫瓦特,简称瓦(W),工程技术上还常用千瓦(KW),兆瓦(MW)作为功率的单位,1KW=1000W,1MW=106W。
功率表示做功的快慢,不表示做功的多少,一个力做功的多少由功率和时间两个因素决定。功率大的机器,做功不一定多;做功多的机械,功率也不一定大。
5计算功率的另一个公式
当物体在动力F的作用下,以速度v沿力F方向做匀速直线运动时,力F所做的功W=Fs=Fvt,,力F做功的功率P=W/t=Fvt/t=Fv。
由P=Fv知,功率一定时,机器的牵引力和速度成反比。
对两个公式的理解
P=W/t是功率的定义式,它表示做功的物体在t时间内的平均功率,而不是某一时刻的瞬时功率,无论受力物体运动状态如何,P=W/t,普遍适用。
P=Fv是功率的推导式,它是当物体在恒力f作用下,以速度v匀速运动时推导出来的,它的表示物体的瞬时功率。
3-4 简单的机械
1杠杆
定义:如果一根硬棒在力的作用下能绕着固定点转动,这根硬棒就叫杠杆。
杠杆可以是直的,也可以是弯的,但它一定是硬棒,既不能变形的棒。
276225049530杠杆的五个要素
支点:杠杆可以绕其转动的点。
动力:使杠杆转动的力。
阻力:阻碍杠杆转动的力。
动力臂:从支点到动力作用线的距离。
阻力臂:从支点到阻力作用线的距离。
要弄清动力臂和阻力臂,首先要弄清”力的作用线”的概念,经过力的作用点,沿着力的方向所引的直线叫力的作用线。力臂就是从支点到力的作用线的距离。
杠杆平衡的条件
杠杆平衡的含义,在力的作用下,如果杠杆处于静止状态或绕支点匀速转动,我们就认为杠杆平衡了。
杠杆平衡条件
动力X动力臂=阻力X阻力臂,用公式表F1l1=F2l2,这个平衡条件就是阿基米德发现的杠杆原理。
杠杆的分类
类型
示意图
力、力臂的关系
特点
应用
省力杠杆
317533020
F1l1>l2
省力费距离。
铡刀、瓶盖起子、手推车、钢丝钳等。
费力杠杆
2540146685
F1>F2
l1费力但省距离
钓鱼竿、镊子、筷子、理发剪、缝纫机脚踏板等
等臂杠杆
F1=F2
l1=l2
既不省力也不省距离,既不费力也不费距离
天平
2定滑轮和动滑轮
定滑轮
定义:轴固定不动的滑轮。
实质:等臂杠杆。
特点:不能省力,但能改变力的方向。
动滑轮
定义:轴与重物一起移动的滑轮。
实质:动力臂为阻力臂两倍的省力杠杆。
特点:使用动滑轮能省一半的力,但费距离,且不能改变力的方向。绳子自由移动的距离是重物移动距离的2倍。
3滑轮组
定义:定滑轮、动滑轮组合在一起构成滑轮组。
特点:使用滑轮组既能省力又能改变力的方向。
滑轮组省力情况分析:F=G/n(其中n为承担物重的绳子的段数)。
绳子自由移动的距离:s=nh(h为重物移动距离)。
滑轮组装的原则:基本原则是”奇动偶定”
4210050395605首先要根据题意求出承担重物的绳子的段数n=G/F(G表示重物,若动滑轮组重不能忽略,则G=G物+G动;F表示所需的拉力)。
→若承担重物的绳子数为奇数,则绳
子的起点从动滑轮开始绕线,如图甲所示;
→若承担重物的绳子数为偶数,则绳
子的起点从定滑轮开始绕线,如图乙所示;
还要注意拉力的方向不同,所需定滑轮的个数也不同。
4机械效率
有用功、额外功、总功
有用功:为了达到某一目的而必须要做的功叫有用功。用W有用表示。
额外功:并非需要,又不得不做的功叫额外功,用W额外表示。
总功:有用功和额外功的总和叫总功,用W总表示,即W总=W有用+W额外。
机械效率
定义:有用功与总功的比值叫机械效率,用?表示。
公式:?=W有用W总 x 100% = W有用W有用+W额外 x 100%。
练习题
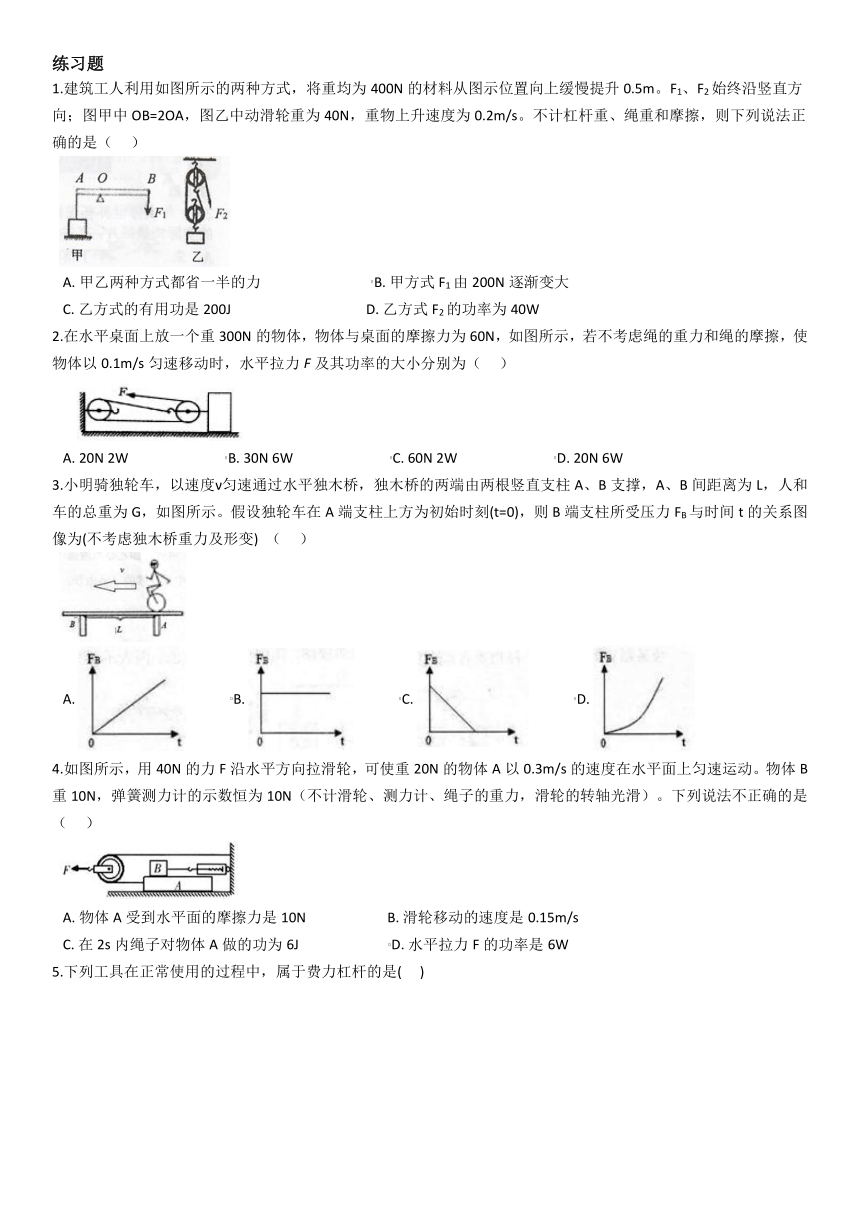
1.建筑工人利用如图所示的两种方式,将重均为400N的材料从图示位置向上缓慢提升0.5m。F1、F2始终沿竖直方向;图甲中OB=2OA,图乙中动滑轮重为40N,重物上升速度为0.2m/s。不计杠杆重、绳重和摩擦,则下列说法正确的是(??? )
A.?甲乙两种方式都省一半的力????????????????????????????????B.?甲方式F1由200N逐渐变大
C.?乙方式的有用功是200J???????????????????????????????????????D.?乙方式F2的功率为40W
2.在水平桌面上放一个重300N的物体,物体与桌面的摩擦力为60N,如图所示,若不考虑绳的重力和绳的摩擦,使物体以0.1m/s匀速移动时,水平拉力F及其功率的大小分别为( ???)
A.?20N 2W????????????????????????????B.?30N 6W????????????????????????????C.?60N 2W????????????????????????????D.?20N 6W
3.小明骑独轮车,以速度ν匀速通过水平独木桥,独木桥的两端由两根竖直支柱A、B支撑,A、B间距离为L,人和车的总重为G,如图所示。假设独轮车在A端支柱上方为初始时刻(t=0),则B端支柱所受压力FB与时间t的关系图像为(不考虑独木桥重力及形变) ( ???)
A.??????????????B.??????????????C.??????????????D.?
4.如图所示,用40N的力F沿水平方向拉滑轮,可使重20N的物体A以0.3m/s的速度在水平面上匀速运动。物体B重10N,弹簧测力计的示数恒为10N(不计滑轮、测力计、绳子的重力,滑轮的转轴光滑)。下列说法不正确的是(??? )
A.?物体A受到水平面的摩擦力是10N???????????????????????B.?滑轮移动的速度是0.15m/s
C.?在2s内绳子对物体A做的功为6J??????????????????????????D.?水平拉力F的功率是6W
5.下列工具在正常使用的过程中,属于费力杠杆的是(??? )
A.?用镊子夹取物体 ??????????????????B.?用钢丝钳剪铁丝
C.?用开瓶器开啤酒 ???????????????D.?用木棍撬石块
6.小金在学习了滑轮之后用下列方法匀速提升同一重物,若不计绳子、滑轮的重力及摩擦,其中最省力的是(??? )
A.??????????????????????B.??????????????????????C.??????????????????????D.?
7.如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车从图示位置向右匀速运动时,下列关于对物体A的分析中正确的是(? ??)
A.?绳的拉力等于A的重力????????????????????????????????????????B.?物体A的动能不变
C.?物体A的机械能匀速增加?????????????????????????????????????D.?绳的拉力对物体A的做功功率不断增加
8.如图所示,在水平地面上放置重300N的物体,不考虑绳的重力和绳与滑轮间的摩擦,匀速拉动物体时,水平拉力F为60N,则物体与地面的摩擦力为________N,若物体前进1米所用的时间为10秒,拉力F做功的功率为________瓦。
9.王强同学设计了如图所示的装置进行实验,其中杠杆OAB支点为O(杠杆OAB质量不计),OA:OB=1:3。他实验的步骤如下:
步骤一:用一细绳将体积为180cm3的金属块悬挂于A点,然后向容器中加水,使金属块浸没在水中。
步骤二:使杠杆OAB在水平位置静止,读出弹簧测力计此时的读数为1.2N。
(1)金属块浸没在水中时受到的浮力为________N。
(2)被测金属块密度:ρ=________?。
10.探究杠杆平衡条件的实验装置如图所示,杠杆上相邻刻度线间距相等。
(1)调节杠杆在水平位置平衡后,在A点挂两个钩码,每个钩码重0.5N,在B点竖直向下拉弹簧测力计,杠杆重新平衡,弹簧测力计的示数为________N。
(2)改变钩码的个数和位置进行了多次实验,其目的是________。
?
答案解析:
1.【解答】A.甲图:根据杠杆的平衡条件得到:G×OA=F1×OB;
400N×1=F1×2;
解得:F1=200N;
乙图:拉力F2=G总n=400N+40N2=220N;
则乙图中的拉力不能省一半的力。
故A错误;
B.甲中,物体静止在水平桌面上,那么A点受到的拉力FA=G-F支持 , 因此FA<400N,那么F1肯定小于200N,故B错误;
C.乙方式的有用功为:W有=Gh=400N×0.5m=200J,故C正确;
D.乙方式中F2的功率为:P2=F2v=220N×(0.2m/s×2)=84W,故D错误。
故选C。
2.【解答】根据图片可知,承担拉力的绳子段数为n=3,
那么水平拉力F=fn=60N3=20N;
水平拉力F移动的速度:v=nv物=3×0.1m/s=0.3m/s;
水平拉力F的功率为:P=Fv=20N×0.3m/s=6W。
故选D。
3.【解答】根据杠杆的平衡条件得到:FB×L=G×s;
即:FB×L=G×vt;
那么B点对桥的支持力FB=GvtL=GvL×t;
其中总重G、速度v和长度L都是定值,因此B点对桥的支持力与时间t成正比;
因为B点对桥的支持力和桥对B点的压力为相互作用力,
所以桥对B点的压力FB与时间t成正比;
那么二者的关系图像应该是通过坐标原点的斜线,故A正确,而B、C、D错误。
故选A。
4.【解答】A.不计滑轮的摩擦和重力,以动滑轮为研究对象,则两段绳子向右的拉力与向左的拉力平衡,所以2F拉=F,则A物体对滑轮的拉力F拉=12F=12×40N=20N;因为力的作用是相互的,所以滑轮对A的拉力也为20N;物体B始终处于静止状态,则测力计对B向右的拉力与A对B向左的摩擦力平衡,所以fA对B=F示=10N;因为力的作用是相互的,所以物体B对A的摩擦力为10N,方向向右;
? ? ?物体A向左匀速运动,它受到绳子向左的拉力,B对它向右的摩擦力和地面对物体A还有向右的摩擦力,由力的平衡条件可得:F拉=fB对A+f地 , 所以地面对A的摩擦力为:f地=F拉-fB对A=20N-10N=10N,故A正确不合题意;
5.【解答】A.用镊子夹取物体,支点在镊片的连接处,阻力在尖端,动力在中间,此时动力臂小于阻力臂,为费力杠杆,故A符合题意;?
B.用钢丝钳剪铁丝,支点在转轴处,阻力在刀口上,动力在手柄上,此时动力臂大于阻力臂,为省力杠杆,故B不合题意;?
C.用开瓶器开啤酒,瓶盖上面的牙为支点,阻力作用在下面的牙上,动力作用在手柄上,此时动力臂大于阻力臂,为省力杠杆,故C不合题意;?
D.用木棍撬石块,木棍的尖端为支点,阻力作用在支点上方附近,动力作用在杠杆的另一端,此时动力臂大于阻力臂,为省力杠杆,故D不合题意。
故选A。
6.【解答】A图:使用动滑轮时,承担重力的绳子为n=2,那么拉力F1=G2;
B图:使用定滑轮时,承担重力的绳子为n=1,那么拉力F2=G;
C图:使用滑轮组,承担重力的绳子为n=3,那么拉力F3=G3;
D图:使用滑轮组时,承担重力的绳子为n=2,那么拉力F4=G2。
因此最省力的是C,故A、B、D不合题意。
故选C。
7.【解答】A.如下图所示:
?
将小车的运动分解为沿绳子方向和垂直于绳子方向,沿绳子方向的分速度等于A的速度,根据平行四边形定则有:vA=vcosθ;因车匀速向右运动,且θ减小,所以A的速度在增大,则A加速上升,即此时物体A受到的合力向上,也就是绳的拉力大于A的重力,故A错误;
物体A的质量不变,但速度增大,所以它的动能不断增大,故B错误;
因为物体A的速度增加量不是匀速的,所以它的机械能的增加也不是匀速的,故C错误;
由于物体A的重力不变,但速度不断增大,根据P=Gv可知,对物体A做功的功率不断增加,故D正确。
故选D。
8.【解答】(1) 物体与地面的摩擦力为?f=nF=2×60N=120N;
(2)自由端前进的距离s=ns物=2×1m=2m;
拉力F做的功为:W=Fs=60N×2m=120J;
拉力F做功的功率为:P=Wt=120J10s=12W。
9.【解答】(1) 金属块浸没在水中时受到的浮力 :
F浮=ρ液gV排=103kg/m3×10N/kg×180×10-6m3=1.8N;
(2)根据杠杆的平衡条件得到:F拉×OA=FB×OB;
F拉×1=1.2N×3;
解得:F拉=3.6N;
金属块的重力为:G=F拉+F浮=3.6N+1.8N=5.4N;
那么金属块的密度为:ρ=GgV=5.4N10N/kg×180×10-6m3=3×103kg/m3。
10.【解答】(1)设杠杆上每个小格的长度为L,根据杠杆的平衡条件F1L1=F2L2得到:
(0.5N×2)×3L=F×2L;
解得:F=1.5N;
(2)改变钩码的个数和位置进行了多次实验,其目的是:避免实验的偶然性,使实验结论具有普遍性。
第八讲 能量转化的量度、简单的机械
3-3 能量转化的量度
1功
定义:如果一个力作用在物体上,且物体在这个力的方向上通过了一段距离,就说这个力对物体做了功。
力对物体做功的两个必要因素: 一是作用在物体上的力,二是物体在这个力的方向上通过了距离。
力不做功的三种情况
三种情况
原因
实例
有距离无力
物体没有受到力的作用,但由于惯性通过了一段距离,就是没有力做功。
足球离开脚后在水平面上滚动了一段距离,人对足球没有做功。
有力无距离
有力作用在物体上,但物体没有动,即物体没有通过距离。
两名同学没有搬起石头,所以对石头没有做功。
力与距离垂直
物体受到力的作用,也移动了一段距离,但通过的距离与力的方向垂直。
提着水桶水平移动了一段距离,竖直提水桶的力不做功
2功的计算
功的计算:功等于力与物体在力的方向上通过的距离的乘积。
公式:用F表示力,s表示力的方向上通过的距离,W表示功,则W=Fs。
单位:在国际单位制中,力的单位是牛,距离的单位是米,的单位是焦耳,简称焦(J)。
1 J = 1N X 1 m=1N??m。
应用W=Fs计算功时,力与物体通过的距离方向必须一致,且对应同一物体,同一段间。
3做功的实质
做功的过程实质就是能量转化的过程,力对物体做了多少功,就有多少能量发生了转化,因此,可以用功来量度能量转化的多少,能量的单位与功的单位一样,也是焦耳。
4功率
定义:功与做功所用的时间之比叫功率,它在数值上等于单位时间内所做的功。
物理意义:功率表示物体做功快慢的物理量。
公式:如果用P表示功率,用W表示功,用t表示做功所用的时间,功率的计算公式为
P=W/t。
单位:在国际单位制中,功的单位是焦,时间的单位是秒,功率的单位是焦耳每秒(J/s),他有一个专门的名称叫瓦特,简称瓦(W),工程技术上还常用千瓦(KW),兆瓦(MW)作为功率的单位,1KW=1000W,1MW=106W。
功率表示做功的快慢,不表示做功的多少,一个力做功的多少由功率和时间两个因素决定。功率大的机器,做功不一定多;做功多的机械,功率也不一定大。
5计算功率的另一个公式
当物体在动力F的作用下,以速度v沿力F方向做匀速直线运动时,力F所做的功W=Fs=Fvt,,力F做功的功率P=W/t=Fvt/t=Fv。
由P=Fv知,功率一定时,机器的牵引力和速度成反比。
对两个公式的理解
P=W/t是功率的定义式,它表示做功的物体在t时间内的平均功率,而不是某一时刻的瞬时功率,无论受力物体运动状态如何,P=W/t,普遍适用。
P=Fv是功率的推导式,它是当物体在恒力f作用下,以速度v匀速运动时推导出来的,它的表示物体的瞬时功率。
3-4 简单的机械
1杠杆
定义:如果一根硬棒在力的作用下能绕着固定点转动,这根硬棒就叫杠杆。
杠杆可以是直的,也可以是弯的,但它一定是硬棒,既不能变形的棒。
276225049530杠杆的五个要素
支点:杠杆可以绕其转动的点。
动力:使杠杆转动的力。
阻力:阻碍杠杆转动的力。
动力臂:从支点到动力作用线的距离。
阻力臂:从支点到阻力作用线的距离。
要弄清动力臂和阻力臂,首先要弄清”力的作用线”的概念,经过力的作用点,沿着力的方向所引的直线叫力的作用线。力臂就是从支点到力的作用线的距离。
杠杆平衡的条件
杠杆平衡的含义,在力的作用下,如果杠杆处于静止状态或绕支点匀速转动,我们就认为杠杆平衡了。
杠杆平衡条件
动力X动力臂=阻力X阻力臂,用公式表F1l1=F2l2,这个平衡条件就是阿基米德发现的杠杆原理。
杠杆的分类
类型
示意图
力、力臂的关系
特点
应用
省力杠杆
317533020
F1
省力费距离。
铡刀、瓶盖起子、手推车、钢丝钳等。
费力杠杆
2540146685
F1>F2
l1
钓鱼竿、镊子、筷子、理发剪、缝纫机脚踏板等
等臂杠杆
F1=F2
l1=l2
既不省力也不省距离,既不费力也不费距离
天平
2定滑轮和动滑轮
定滑轮
定义:轴固定不动的滑轮。
实质:等臂杠杆。
特点:不能省力,但能改变力的方向。
动滑轮
定义:轴与重物一起移动的滑轮。
实质:动力臂为阻力臂两倍的省力杠杆。
特点:使用动滑轮能省一半的力,但费距离,且不能改变力的方向。绳子自由移动的距离是重物移动距离的2倍。
3滑轮组
定义:定滑轮、动滑轮组合在一起构成滑轮组。
特点:使用滑轮组既能省力又能改变力的方向。
滑轮组省力情况分析:F=G/n(其中n为承担物重的绳子的段数)。
绳子自由移动的距离:s=nh(h为重物移动距离)。
滑轮组装的原则:基本原则是”奇动偶定”
4210050395605首先要根据题意求出承担重物的绳子的段数n=G/F(G表示重物,若动滑轮组重不能忽略,则G=G物+G动;F表示所需的拉力)。
→若承担重物的绳子数为奇数,则绳
子的起点从动滑轮开始绕线,如图甲所示;
→若承担重物的绳子数为偶数,则绳
子的起点从定滑轮开始绕线,如图乙所示;
还要注意拉力的方向不同,所需定滑轮的个数也不同。
4机械效率
有用功、额外功、总功
有用功:为了达到某一目的而必须要做的功叫有用功。用W有用表示。
额外功:并非需要,又不得不做的功叫额外功,用W额外表示。
总功:有用功和额外功的总和叫总功,用W总表示,即W总=W有用+W额外。
机械效率
定义:有用功与总功的比值叫机械效率,用?表示。
公式:?=W有用W总 x 100% = W有用W有用+W额外 x 100%。
练习题
1.建筑工人利用如图所示的两种方式,将重均为400N的材料从图示位置向上缓慢提升0.5m。F1、F2始终沿竖直方向;图甲中OB=2OA,图乙中动滑轮重为40N,重物上升速度为0.2m/s。不计杠杆重、绳重和摩擦,则下列说法正确的是(??? )
A.?甲乙两种方式都省一半的力????????????????????????????????B.?甲方式F1由200N逐渐变大
C.?乙方式的有用功是200J???????????????????????????????????????D.?乙方式F2的功率为40W
2.在水平桌面上放一个重300N的物体,物体与桌面的摩擦力为60N,如图所示,若不考虑绳的重力和绳的摩擦,使物体以0.1m/s匀速移动时,水平拉力F及其功率的大小分别为( ???)
A.?20N 2W????????????????????????????B.?30N 6W????????????????????????????C.?60N 2W????????????????????????????D.?20N 6W
3.小明骑独轮车,以速度ν匀速通过水平独木桥,独木桥的两端由两根竖直支柱A、B支撑,A、B间距离为L,人和车的总重为G,如图所示。假设独轮车在A端支柱上方为初始时刻(t=0),则B端支柱所受压力FB与时间t的关系图像为(不考虑独木桥重力及形变) ( ???)
A.??????????????B.??????????????C.??????????????D.?
4.如图所示,用40N的力F沿水平方向拉滑轮,可使重20N的物体A以0.3m/s的速度在水平面上匀速运动。物体B重10N,弹簧测力计的示数恒为10N(不计滑轮、测力计、绳子的重力,滑轮的转轴光滑)。下列说法不正确的是(??? )
A.?物体A受到水平面的摩擦力是10N???????????????????????B.?滑轮移动的速度是0.15m/s
C.?在2s内绳子对物体A做的功为6J??????????????????????????D.?水平拉力F的功率是6W
5.下列工具在正常使用的过程中,属于费力杠杆的是(??? )
A.?用镊子夹取物体 ??????????????????B.?用钢丝钳剪铁丝
C.?用开瓶器开啤酒 ???????????????D.?用木棍撬石块
6.小金在学习了滑轮之后用下列方法匀速提升同一重物,若不计绳子、滑轮的重力及摩擦,其中最省力的是(??? )
A.??????????????????????B.??????????????????????C.??????????????????????D.?
7.如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车从图示位置向右匀速运动时,下列关于对物体A的分析中正确的是(? ??)
A.?绳的拉力等于A的重力????????????????????????????????????????B.?物体A的动能不变
C.?物体A的机械能匀速增加?????????????????????????????????????D.?绳的拉力对物体A的做功功率不断增加
8.如图所示,在水平地面上放置重300N的物体,不考虑绳的重力和绳与滑轮间的摩擦,匀速拉动物体时,水平拉力F为60N,则物体与地面的摩擦力为________N,若物体前进1米所用的时间为10秒,拉力F做功的功率为________瓦。
9.王强同学设计了如图所示的装置进行实验,其中杠杆OAB支点为O(杠杆OAB质量不计),OA:OB=1:3。他实验的步骤如下:
步骤一:用一细绳将体积为180cm3的金属块悬挂于A点,然后向容器中加水,使金属块浸没在水中。
步骤二:使杠杆OAB在水平位置静止,读出弹簧测力计此时的读数为1.2N。
(1)金属块浸没在水中时受到的浮力为________N。
(2)被测金属块密度:ρ=________?。
10.探究杠杆平衡条件的实验装置如图所示,杠杆上相邻刻度线间距相等。
(1)调节杠杆在水平位置平衡后,在A点挂两个钩码,每个钩码重0.5N,在B点竖直向下拉弹簧测力计,杠杆重新平衡,弹簧测力计的示数为________N。
(2)改变钩码的个数和位置进行了多次实验,其目的是________。
?
答案解析:
1.【解答】A.甲图:根据杠杆的平衡条件得到:G×OA=F1×OB;
400N×1=F1×2;
解得:F1=200N;
乙图:拉力F2=G总n=400N+40N2=220N;
则乙图中的拉力不能省一半的力。
故A错误;
B.甲中,物体静止在水平桌面上,那么A点受到的拉力FA=G-F支持 , 因此FA<400N,那么F1肯定小于200N,故B错误;
C.乙方式的有用功为:W有=Gh=400N×0.5m=200J,故C正确;
D.乙方式中F2的功率为:P2=F2v=220N×(0.2m/s×2)=84W,故D错误。
故选C。
2.【解答】根据图片可知,承担拉力的绳子段数为n=3,
那么水平拉力F=fn=60N3=20N;
水平拉力F移动的速度:v=nv物=3×0.1m/s=0.3m/s;
水平拉力F的功率为:P=Fv=20N×0.3m/s=6W。
故选D。
3.【解答】根据杠杆的平衡条件得到:FB×L=G×s;
即:FB×L=G×vt;
那么B点对桥的支持力FB=GvtL=GvL×t;
其中总重G、速度v和长度L都是定值,因此B点对桥的支持力与时间t成正比;
因为B点对桥的支持力和桥对B点的压力为相互作用力,
所以桥对B点的压力FB与时间t成正比;
那么二者的关系图像应该是通过坐标原点的斜线,故A正确,而B、C、D错误。
故选A。
4.【解答】A.不计滑轮的摩擦和重力,以动滑轮为研究对象,则两段绳子向右的拉力与向左的拉力平衡,所以2F拉=F,则A物体对滑轮的拉力F拉=12F=12×40N=20N;因为力的作用是相互的,所以滑轮对A的拉力也为20N;物体B始终处于静止状态,则测力计对B向右的拉力与A对B向左的摩擦力平衡,所以fA对B=F示=10N;因为力的作用是相互的,所以物体B对A的摩擦力为10N,方向向右;
? ? ?物体A向左匀速运动,它受到绳子向左的拉力,B对它向右的摩擦力和地面对物体A还有向右的摩擦力,由力的平衡条件可得:F拉=fB对A+f地 , 所以地面对A的摩擦力为:f地=F拉-fB对A=20N-10N=10N,故A正确不合题意;
5.【解答】A.用镊子夹取物体,支点在镊片的连接处,阻力在尖端,动力在中间,此时动力臂小于阻力臂,为费力杠杆,故A符合题意;?
B.用钢丝钳剪铁丝,支点在转轴处,阻力在刀口上,动力在手柄上,此时动力臂大于阻力臂,为省力杠杆,故B不合题意;?
C.用开瓶器开啤酒,瓶盖上面的牙为支点,阻力作用在下面的牙上,动力作用在手柄上,此时动力臂大于阻力臂,为省力杠杆,故C不合题意;?
D.用木棍撬石块,木棍的尖端为支点,阻力作用在支点上方附近,动力作用在杠杆的另一端,此时动力臂大于阻力臂,为省力杠杆,故D不合题意。
故选A。
6.【解答】A图:使用动滑轮时,承担重力的绳子为n=2,那么拉力F1=G2;
B图:使用定滑轮时,承担重力的绳子为n=1,那么拉力F2=G;
C图:使用滑轮组,承担重力的绳子为n=3,那么拉力F3=G3;
D图:使用滑轮组时,承担重力的绳子为n=2,那么拉力F4=G2。
因此最省力的是C,故A、B、D不合题意。
故选C。
7.【解答】A.如下图所示:
?
将小车的运动分解为沿绳子方向和垂直于绳子方向,沿绳子方向的分速度等于A的速度,根据平行四边形定则有:vA=vcosθ;因车匀速向右运动,且θ减小,所以A的速度在增大,则A加速上升,即此时物体A受到的合力向上,也就是绳的拉力大于A的重力,故A错误;
物体A的质量不变,但速度增大,所以它的动能不断增大,故B错误;
因为物体A的速度增加量不是匀速的,所以它的机械能的增加也不是匀速的,故C错误;
由于物体A的重力不变,但速度不断增大,根据P=Gv可知,对物体A做功的功率不断增加,故D正确。
故选D。
8.【解答】(1) 物体与地面的摩擦力为?f=nF=2×60N=120N;
(2)自由端前进的距离s=ns物=2×1m=2m;
拉力F做的功为:W=Fs=60N×2m=120J;
拉力F做功的功率为:P=Wt=120J10s=12W。
9.【解答】(1) 金属块浸没在水中时受到的浮力 :
F浮=ρ液gV排=103kg/m3×10N/kg×180×10-6m3=1.8N;
(2)根据杠杆的平衡条件得到:F拉×OA=FB×OB;
F拉×1=1.2N×3;
解得:F拉=3.6N;
金属块的重力为:G=F拉+F浮=3.6N+1.8N=5.4N;
那么金属块的密度为:ρ=GgV=5.4N10N/kg×180×10-6m3=3×103kg/m3。
10.【解答】(1)设杠杆上每个小格的长度为L,根据杠杆的平衡条件F1L1=F2L2得到:
(0.5N×2)×3L=F×2L;
解得:F=1.5N;
(2)改变钩码的个数和位置进行了多次实验,其目的是:避免实验的偶然性,使实验结论具有普遍性。
同课章节目录
- 第1章 物质及其变化
- 第1节 物质的变化
- 第2节 物质的酸碱性
- 第3节 常见的酸
- 第4节 常见的碱
- 第5节 酸和碱之间发生的反应
- 第6节 几种重要的盐
- 第2章 物质转化与材料利用
- 第1节 金属材料
- 第2节 金属的化学性质
- 第3节 有机物和有机合成材料
- 第4节 物质的分类
- 第5节 物质的转化
- 第6节 材料的利用与发展
- 第3章 能量的转化与守恒
- 第1节 能量及其形式
- 第2节 机械能
- 第3节 能量转化的量度
- 第4节 简单机械
- 第5节 物体的内能
- 第6节 电能
- 第7节 核能
- 第8节 能量的转化与守恒
- 第4章 代谢与平衡
- 第1节 食物与营养
- 第2节 食物的消化与吸收
- 第3节 体内物质的运输
- 第4节 能量的获得
- 第5节 体内物质的动态平衡
- 研究性学习课题
- 一 当地酸雨情况以及对农作物和建筑物的影响
- 二 金属对社会发展的作用
- 三 寻找自行车中的杠杆
- 四 怎样防治龋齿
