人教版八年级数学下册课时作业:17.1 第2课时 勾股定理在实际生活中的应用(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学下册课时作业:17.1 第2课时 勾股定理在实际生活中的应用(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 216.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 08:50:30 | ||
图片预览


文档简介
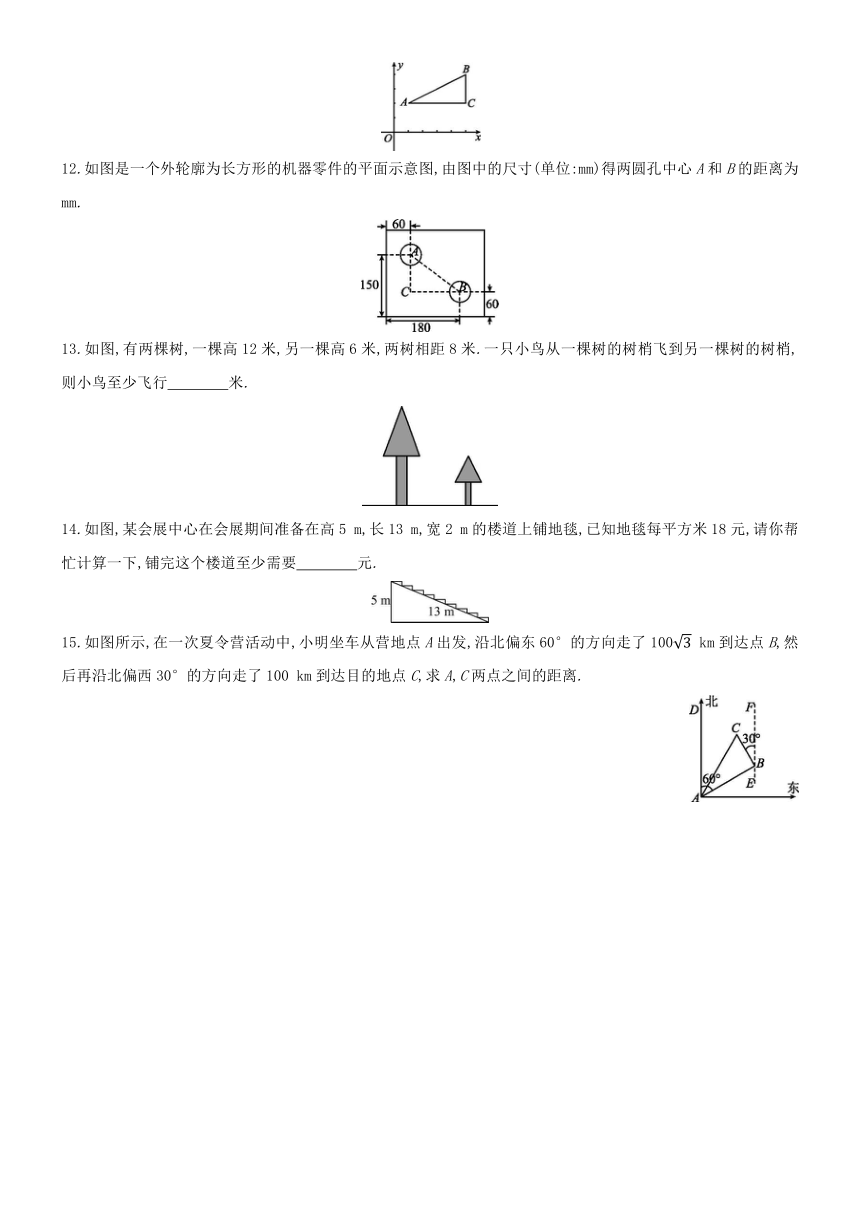
第2课时 勾股定理在实际生活中的应用
知识点1 已知直角三角形的两边求第三边
1.如果梯子的底端离一幢楼5米,那么13米长的梯子可以达到该楼的高度是
( )
A.12米
B.13米
C.14米
D.15米
2.如图是某校的长方形操场,一学生从A角走到C角,至少要走
( )
A.140米
B.120米
C.100米
D.90米
3.由于受台风的影响,一棵树在离地面6
m处折断(如图),树顶落在离树干底部8
m处,则这棵树在折断前的高度是
( )
A.8
m
B.10
m
C.16
m
D.18
m
4.王英在池塘边观看荷花时,她把一株竖直的荷花(如图)拉到岸边,花柄正好与岸边成60°夹角,测得AB长60
cm,则荷花处的水深OA为 cm.?
5.如图,某人划船横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B25
m,结果他沿直线在水中实际划了65
m,求该河流的宽度.
6.如图,修公路时遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,过点C作直线AB的垂线l,过点B作一直线(在山的旁边经过),与l相交于点D,经测量∠ABD=135°,BD=800米,则应在直线l上距离点D多远的C处开挖?(≈1.414,结果精确到1米)
知识点2 已知直角三角形的一边和两边之间的关系求第三边
7.小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面后还多1
m,当他把绳子的下端拉开4
m后,发现下端刚好接触地面,则旗杆的高为
( )
A.7
m
B.7.5
m
C.8
m
D.9
m
8.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何.”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.若设AC=x,则可列方程为
.?
9.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙上,梯子底端到左墙脚的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙上,顶端距离地面2米,那么小巷的宽度为
( )
A.0.7米
B.1.5米
C.2.2米
D.2.4米
10.如图,将一根长16
cm的筷子置于底面直径为5
cm,高为12
cm的圆柱形水杯中,设筷子露在杯子外面的长度为h
cm,则h的取值范围是
( )
A.4≤h≤11
B.4≤h≤5
C.3≤h≤4
D.5≤h≤12
11.如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(1,2),C(5,2),B(5,4),则AB的长为 .?
12.如图是一个外轮廓为长方形的机器零件的平面示意图,由图中的尺寸(单位:mm)得两圆孔中心A和B的距离为 mm.?
13.如图,有两棵树,一棵高12米,另一棵高6米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行 米.?
14.如图,某会展中心在会展期间准备在高5
m,长13
m,宽2
m的楼道上铺地毯,已知地毯每平方米18元,请你帮忙计算一下,铺完这个楼道至少需要 元.?
15.如图所示,在一次夏令营活动中,小明坐车从营地点A出发,沿北偏东60°的方向走了100
km到达点B,然后再沿北偏西30°的方向走了100
km到达目的地点C,求A,C两点之间的距离.
16.如图,一架梯子AB长25米,将其斜靠在一面墙上.
(1)若梯子底端到墙脚的距离OB=7米,则这架梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端向下滑动了4米,那么梯子的底端在水平方向滑动了多少米?
(3)在(1)(2)的条件下,发现梯子在滑动过程中,滑动距离AA'和BB'可以相等,请你直接写出这个滑动距离.
答案
1.A
2.C 解析:
连接AC.因为两点之间线段最短,所以AC的长即为从A到C的最短距离.根据长方形的对边相等,得BC=AD=80米,再根据勾股定理,得AC==100(米).
3.C 解析:
如图,AB===10(m),所以AC+AB=6+10=16(m),所以这棵树在折断前的高度是16
m.故选C.
4.60 解析:
在Rt△ABO中,∠OAB=90°,∠ABO=60°,AB=60
cm,∴∠AOB=30°,
∴OB=2AB=120
cm,
∴OA===60(cm).
故答案为60.
5.解:由题意知△ABC为直角三角形且∠ABC=90°.由勾股定理可得
AB===60(m),
所以该河流的宽度为60
m.
6.解:∵CD⊥AC,
∴∠ACD=90°.
∵∠ABD=135°,
∴∠DBC=45°,
∴∠BDC=45°,
∴BC=CD.
在Rt△DCB中,CD2+BC2=BD2,
即2CD2=8002,
∴CD=400≈566(米).
答:应在直线l上距离点D约566米的C处开挖.
7.B 解析:
如图所示,设旗杆的高AB=x
m,则AC=(x+1)m.
在Rt△ABC中,AC2=AB2+BC2,即(x+1)2=x2+42,解得x=7.5.
8.x2+32=(10-x)2 解析:
∵AC=x,AC+AB=10,∴AB=10-x.
∵在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,即x2+32=(10-x)2.
9.C 解析:
如图,在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,
∴AB2=0.72+2.42=6.25.
在Rt△A'BD中,∵∠A'DB=90°,A'D=2米,BD2+A'D2=A'B2,
∴BD2+22=6.25,∴BD2=2.25,
∴BD==1.5(米),∴CD=BC+BD=0.7+1.5=2.2(米).故选C.
10.C 解析:
当筷子与杯底垂直时h最大,h最大为16-12=4.
当筷子与杯底及杯身构成直角三角形时h最小,
此时,杯内筷子的长度最大为=13(cm),
故h最小为16-13=3.
故h的取值范围是3≤h≤4.
故选C.
11.2 解析:
∵△ABC各顶点的坐标分别为A(1,2),C(5,2),B(5,4),
∴AC⊥BC,AC=5-1=4,BC=4-2=2.
根据勾股定理,得AB===2.
12.150 解析:
由已知可得AC=90
mm,BC=120
mm,根据勾股定理,得AB=150
mm.
13.10 解析:
如图,大树高AB=12
米,小树高CD=6
米.
过点C作CE⊥AB于点E,连接AC,则EB=6
米,EC=8
米,AE=AB-EB=12-6=6(米).在Rt△AEC中,AC==10(米).故小鸟至少飞行10
米.
14.612
解析:
由勾股定理,得AC===12(m),
则地毯的长度为12+5=17(m),
则地毯的面积为17×2=34(m2),
所以铺完这个楼道至少需要34×18=612(元).
故答案为612.
15.解:∵AD∥BE,
∴∠ABE=∠DAB=60°.
∵∠CBF=30°,
∴∠ABC=180°-∠ABE-∠CBF=180°-60°-30°=90°.
在Rt△ABC中,AB=100
km,BC=100
km,
∴AC===200(km),
∴A,C两点之间的距离为200
km.
16.解:(1)在Rt△AOB中,AB=25米,OB=7米,由勾股定理,得OA===24(米).
答:梯子的顶端距地面24米.
(2)在Rt△A'OB'中,A'B'=25米,OA'=24-4=20(米),
由勾股定理,得OB'===15(米),
所以BB'=OB'-OB=15-7=8(米).
答:梯子的底端在水平方向滑动了8米.
(3)17米.
知识点1 已知直角三角形的两边求第三边
1.如果梯子的底端离一幢楼5米,那么13米长的梯子可以达到该楼的高度是
( )
A.12米
B.13米
C.14米
D.15米
2.如图是某校的长方形操场,一学生从A角走到C角,至少要走
( )
A.140米
B.120米
C.100米
D.90米
3.由于受台风的影响,一棵树在离地面6
m处折断(如图),树顶落在离树干底部8
m处,则这棵树在折断前的高度是
( )
A.8
m
B.10
m
C.16
m
D.18
m
4.王英在池塘边观看荷花时,她把一株竖直的荷花(如图)拉到岸边,花柄正好与岸边成60°夹角,测得AB长60
cm,则荷花处的水深OA为 cm.?
5.如图,某人划船横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B25
m,结果他沿直线在水中实际划了65
m,求该河流的宽度.
6.如图,修公路时遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,过点C作直线AB的垂线l,过点B作一直线(在山的旁边经过),与l相交于点D,经测量∠ABD=135°,BD=800米,则应在直线l上距离点D多远的C处开挖?(≈1.414,结果精确到1米)
知识点2 已知直角三角形的一边和两边之间的关系求第三边
7.小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面后还多1
m,当他把绳子的下端拉开4
m后,发现下端刚好接触地面,则旗杆的高为
( )
A.7
m
B.7.5
m
C.8
m
D.9
m
8.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何.”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长.若设AC=x,则可列方程为
.?
9.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙上,梯子底端到左墙脚的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙上,顶端距离地面2米,那么小巷的宽度为
( )
A.0.7米
B.1.5米
C.2.2米
D.2.4米
10.如图,将一根长16
cm的筷子置于底面直径为5
cm,高为12
cm的圆柱形水杯中,设筷子露在杯子外面的长度为h
cm,则h的取值范围是
( )
A.4≤h≤11
B.4≤h≤5
C.3≤h≤4
D.5≤h≤12
11.如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(1,2),C(5,2),B(5,4),则AB的长为 .?
12.如图是一个外轮廓为长方形的机器零件的平面示意图,由图中的尺寸(单位:mm)得两圆孔中心A和B的距离为 mm.?
13.如图,有两棵树,一棵高12米,另一棵高6米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行 米.?
14.如图,某会展中心在会展期间准备在高5
m,长13
m,宽2
m的楼道上铺地毯,已知地毯每平方米18元,请你帮忙计算一下,铺完这个楼道至少需要 元.?
15.如图所示,在一次夏令营活动中,小明坐车从营地点A出发,沿北偏东60°的方向走了100
km到达点B,然后再沿北偏西30°的方向走了100
km到达目的地点C,求A,C两点之间的距离.
16.如图,一架梯子AB长25米,将其斜靠在一面墙上.
(1)若梯子底端到墙脚的距离OB=7米,则这架梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端向下滑动了4米,那么梯子的底端在水平方向滑动了多少米?
(3)在(1)(2)的条件下,发现梯子在滑动过程中,滑动距离AA'和BB'可以相等,请你直接写出这个滑动距离.
答案
1.A
2.C 解析:
连接AC.因为两点之间线段最短,所以AC的长即为从A到C的最短距离.根据长方形的对边相等,得BC=AD=80米,再根据勾股定理,得AC==100(米).
3.C 解析:
如图,AB===10(m),所以AC+AB=6+10=16(m),所以这棵树在折断前的高度是16
m.故选C.
4.60 解析:
在Rt△ABO中,∠OAB=90°,∠ABO=60°,AB=60
cm,∴∠AOB=30°,
∴OB=2AB=120
cm,
∴OA===60(cm).
故答案为60.
5.解:由题意知△ABC为直角三角形且∠ABC=90°.由勾股定理可得
AB===60(m),
所以该河流的宽度为60
m.
6.解:∵CD⊥AC,
∴∠ACD=90°.
∵∠ABD=135°,
∴∠DBC=45°,
∴∠BDC=45°,
∴BC=CD.
在Rt△DCB中,CD2+BC2=BD2,
即2CD2=8002,
∴CD=400≈566(米).
答:应在直线l上距离点D约566米的C处开挖.
7.B 解析:
如图所示,设旗杆的高AB=x
m,则AC=(x+1)m.
在Rt△ABC中,AC2=AB2+BC2,即(x+1)2=x2+42,解得x=7.5.
8.x2+32=(10-x)2 解析:
∵AC=x,AC+AB=10,∴AB=10-x.
∵在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,即x2+32=(10-x)2.
9.C 解析:
如图,在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,
∴AB2=0.72+2.42=6.25.
在Rt△A'BD中,∵∠A'DB=90°,A'D=2米,BD2+A'D2=A'B2,
∴BD2+22=6.25,∴BD2=2.25,
∴BD==1.5(米),∴CD=BC+BD=0.7+1.5=2.2(米).故选C.
10.C 解析:
当筷子与杯底垂直时h最大,h最大为16-12=4.
当筷子与杯底及杯身构成直角三角形时h最小,
此时,杯内筷子的长度最大为=13(cm),
故h最小为16-13=3.
故h的取值范围是3≤h≤4.
故选C.
11.2 解析:
∵△ABC各顶点的坐标分别为A(1,2),C(5,2),B(5,4),
∴AC⊥BC,AC=5-1=4,BC=4-2=2.
根据勾股定理,得AB===2.
12.150 解析:
由已知可得AC=90
mm,BC=120
mm,根据勾股定理,得AB=150
mm.
13.10 解析:
如图,大树高AB=12
米,小树高CD=6
米.
过点C作CE⊥AB于点E,连接AC,则EB=6
米,EC=8
米,AE=AB-EB=12-6=6(米).在Rt△AEC中,AC==10(米).故小鸟至少飞行10
米.
14.612
解析:
由勾股定理,得AC===12(m),
则地毯的长度为12+5=17(m),
则地毯的面积为17×2=34(m2),
所以铺完这个楼道至少需要34×18=612(元).
故答案为612.
15.解:∵AD∥BE,
∴∠ABE=∠DAB=60°.
∵∠CBF=30°,
∴∠ABC=180°-∠ABE-∠CBF=180°-60°-30°=90°.
在Rt△ABC中,AB=100
km,BC=100
km,
∴AC===200(km),
∴A,C两点之间的距离为200
km.
16.解:(1)在Rt△AOB中,AB=25米,OB=7米,由勾股定理,得OA===24(米).
答:梯子的顶端距地面24米.
(2)在Rt△A'OB'中,A'B'=25米,OA'=24-4=20(米),
由勾股定理,得OB'===15(米),
所以BB'=OB'-OB=15-7=8(米).
答:梯子的底端在水平方向滑动了8米.
(3)17米.
