人教版八年级数学下册课时作业:17.1 第3课时 勾股定理作图与计算(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学下册课时作业:17.1 第3课时 勾股定理作图与计算(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 373.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 00:00:00 | ||
图片预览


文档简介
第3课时 勾股定理作图与计算
知识点
1 勾股定理与实数
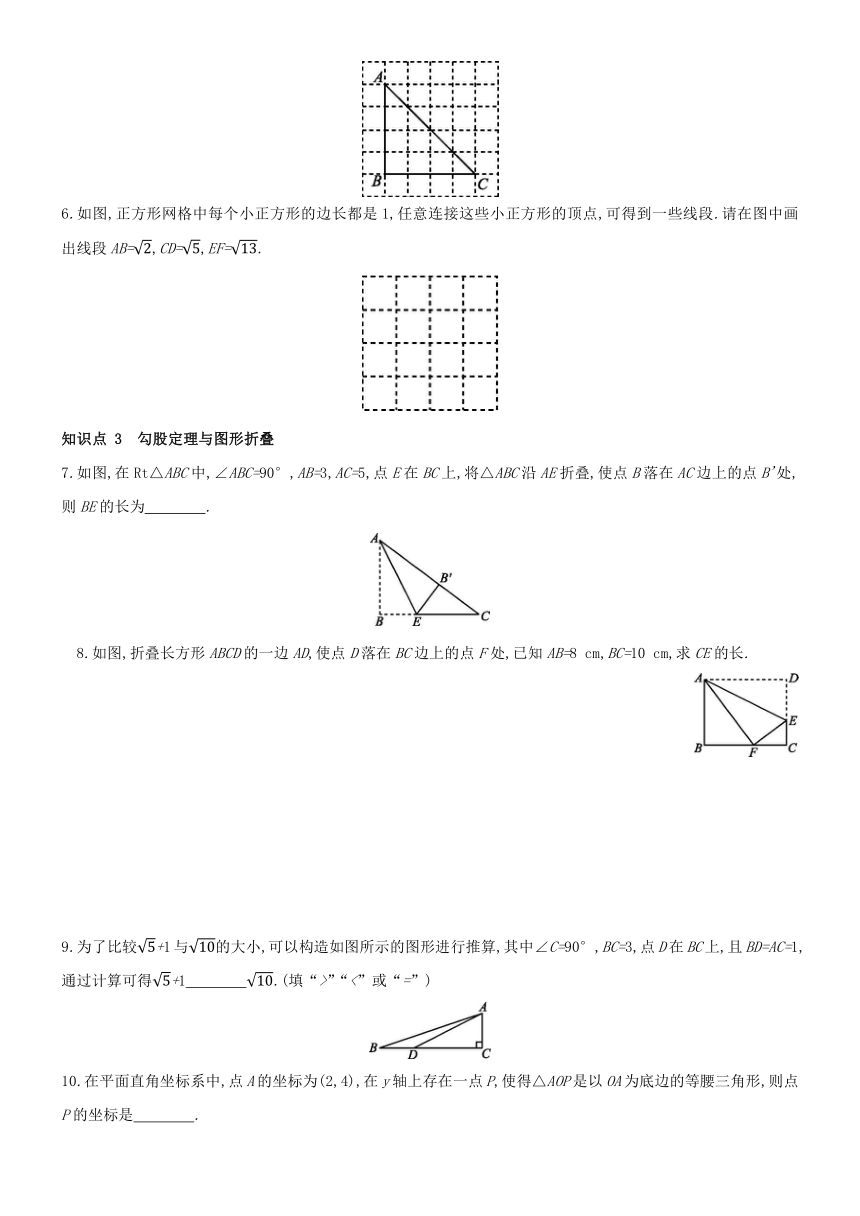
1.小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:如图,首先画出数轴,设原点为点O,在数轴上距原点2个单位长度的位置确定一点A,然后过点A作AB⊥OA,且AB=3.以点O为圆心,OB长为半径作弧,与数轴右侧的交点记为点P,则点P表示的实数在
( )
A.1和2之间
B.2和3之间
C.3和4之间
D.4和5之间
2.如图所示,在正方形ODBC中,OC=2,OA=OB,则数轴上点A表示的数是 .?
知识点
2 勾股定理与网格
3.如图,点A,B,C在正方形网格的格点上,每个小正方形的边长均为1,则网格上的△ABC的三边中,长度为无理数的边有
( )
A.0条
B.1条
C.2条
D.3条
4.如图,网格中每个小正方形的边长都为1,则△ABC的周长为
( )
A.16
B.12+4
C.7+7
D.5+11
5.如图,在6×6的正方形网格(每个小正方形的边长均为1
cm)中,网格线的交点称为格点,△ABC的顶点都在格点处,则AC边上的高为 cm.?
6.如图,正方形网格中每个小正方形的边长都是1,任意连接这些小正方形的顶点,可得到一些线段.请在图中画出线段AB=,CD=,EF=.
知识点
3 勾股定理与图形折叠
7.如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B'处,则BE的长为 .?
8.如图,折叠长方形ABCD的一边AD,使点D落在BC边上的点F处,已知AB=8
cm,BC=10
cm,求CE的长.
9.为了比较+1与的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=3,点D在BC上,且BD=AC=1,通过计算可得+1 ?.(填“>”“<”或“=”)
10.在平面直角坐标系中,点A的坐标为(2,4),在y轴上存在一点P,使得△AOP是以OA为底边的等腰三角形,则点P的坐标是 .?
11.在平面直角坐标系中,分别描出点A(-3,0),B(2,0),C(1,3),再用线段将这三点顺次连接起来,得到△ABC,求△ABC的周长与面积.
12.如图是4张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长都是1,请在方格纸中分别画出符合下列要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:
(1)画一个三边长分别为3,,的三角形;
(2)画一个一条直角边长为4,面积为6的直角三角形;
(3)画一个底边长为4,面积为8的等腰三角形;
(4)画一个面积为5的等腰直角三角形.
13.图①是第七届国际数学教育大会的会徽,会徽的主体图案是由图②中的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1.
细心观察图形,认真分析下列各式,然后解答问题:
()2+1=2,S1=;()2+1=3,S2=;()2+1=4,S3=,….
(1)请用含有n(n是正整数)的等式表示上述变化规律,并计算出OA10的长;
(2)求出+++…+的值.
答案
1.C 解析:
由勾股定理得OB==.∵9<13<16,∴3<<4,∴点P表示的实数在3和4之间.
2.-2 解析:
∵四边形ODBC是正方形,∴BC=OC=2,∠BCO=90°.根据勾股定理,得OB=2,∴点A表示的数是-2.
3.C 解析:
由勾股定理得AC==5,是有理数,不是无理数;
BC==,是无理数;
AB==,是无理数,
即网格上的△ABC的三边中,长度为无理数的边有2条.故选C.
4.B 解析:
根据勾股定理可知AB==5,BC==4,则△ABC的周长为AB+BC+AC=5+4+7=12+4.
5.2 解析:
在Rt△ABC中,AB=4
cm,BC=4
cm,
由勾股定理知,AC===4(cm).
设AC边上的高为h
cm,则AB·BC=AC·h,
∴h===2.
故答案是2.
6.解:如图:
7. 解析:
BC==4.
由折叠的性质,得BE=B'E,AB=AB'.
设BE=x,则B'E=x,CE=4-x,B'C=AC-AB'=AC-AB=2.
在Rt△B'EC中,B'E2+B'C2=CE2,
即x2+22=(4-x)2,
解得x=.
8.解:由题意,知BC=AD=AF=10
cm,DE=EF.
在Rt△ABF中,BF===6(cm),
∴CF=BC-BF=4
cm.
设CE=x
cm,则DE=EF=(8-x)cm.
在Rt△FEC中,由勾股定理,
得CF2+CE2=EF2,即42+x2=(8-x)2,
解得x=3,即CE=3
cm.
9.> 解析:
∵∠C=90°,BC=3,BD=AC=1,∴CD=2,AB==,
∴AD==,
∴AD+BD=+1.
又∵△ABD中,AD+BD>AB,
∴+1>.
10.0,
11.解:如图:
利用勾股定理,得AC==5,BC==,AB=2-(-3)=5,
∴△ABC的周长为AC+BC+AB=5++5=10+,△ABC的面积为×5×3=.
12.解:(1)如图①所示.
(2)如图②所示.
(3)如图③所示.
(4)如图④所示.
13.解:(1)根据勾股定理,得OA2=,OA3=,OA4=2,…,OA10=,…,OAn=.
S1=,S2=,S3=,…,S10=,…,Sn=.
(2)+++…+=2+2+2+…+2==.
知识点
1 勾股定理与实数
1.小明学了利用勾股定理在数轴上找一个无理数的准确位置后,又进一步进行练习:如图,首先画出数轴,设原点为点O,在数轴上距原点2个单位长度的位置确定一点A,然后过点A作AB⊥OA,且AB=3.以点O为圆心,OB长为半径作弧,与数轴右侧的交点记为点P,则点P表示的实数在
( )
A.1和2之间
B.2和3之间
C.3和4之间
D.4和5之间
2.如图所示,在正方形ODBC中,OC=2,OA=OB,则数轴上点A表示的数是 .?
知识点
2 勾股定理与网格
3.如图,点A,B,C在正方形网格的格点上,每个小正方形的边长均为1,则网格上的△ABC的三边中,长度为无理数的边有
( )
A.0条
B.1条
C.2条
D.3条
4.如图,网格中每个小正方形的边长都为1,则△ABC的周长为
( )
A.16
B.12+4
C.7+7
D.5+11
5.如图,在6×6的正方形网格(每个小正方形的边长均为1
cm)中,网格线的交点称为格点,△ABC的顶点都在格点处,则AC边上的高为 cm.?
6.如图,正方形网格中每个小正方形的边长都是1,任意连接这些小正方形的顶点,可得到一些线段.请在图中画出线段AB=,CD=,EF=.
知识点
3 勾股定理与图形折叠
7.如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B'处,则BE的长为 .?
8.如图,折叠长方形ABCD的一边AD,使点D落在BC边上的点F处,已知AB=8
cm,BC=10
cm,求CE的长.
9.为了比较+1与的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=3,点D在BC上,且BD=AC=1,通过计算可得+1 ?.(填“>”“<”或“=”)
10.在平面直角坐标系中,点A的坐标为(2,4),在y轴上存在一点P,使得△AOP是以OA为底边的等腰三角形,则点P的坐标是 .?
11.在平面直角坐标系中,分别描出点A(-3,0),B(2,0),C(1,3),再用线段将这三点顺次连接起来,得到△ABC,求△ABC的周长与面积.
12.如图是4张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长都是1,请在方格纸中分别画出符合下列要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:
(1)画一个三边长分别为3,,的三角形;
(2)画一个一条直角边长为4,面积为6的直角三角形;
(3)画一个底边长为4,面积为8的等腰三角形;
(4)画一个面积为5的等腰直角三角形.
13.图①是第七届国际数学教育大会的会徽,会徽的主体图案是由图②中的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1.
细心观察图形,认真分析下列各式,然后解答问题:
()2+1=2,S1=;()2+1=3,S2=;()2+1=4,S3=,….
(1)请用含有n(n是正整数)的等式表示上述变化规律,并计算出OA10的长;
(2)求出+++…+的值.
答案
1.C 解析:
由勾股定理得OB==.∵9<13<16,∴3<<4,∴点P表示的实数在3和4之间.
2.-2 解析:
∵四边形ODBC是正方形,∴BC=OC=2,∠BCO=90°.根据勾股定理,得OB=2,∴点A表示的数是-2.
3.C 解析:
由勾股定理得AC==5,是有理数,不是无理数;
BC==,是无理数;
AB==,是无理数,
即网格上的△ABC的三边中,长度为无理数的边有2条.故选C.
4.B 解析:
根据勾股定理可知AB==5,BC==4,则△ABC的周长为AB+BC+AC=5+4+7=12+4.
5.2 解析:
在Rt△ABC中,AB=4
cm,BC=4
cm,
由勾股定理知,AC===4(cm).
设AC边上的高为h
cm,则AB·BC=AC·h,
∴h===2.
故答案是2.
6.解:如图:
7. 解析:
BC==4.
由折叠的性质,得BE=B'E,AB=AB'.
设BE=x,则B'E=x,CE=4-x,B'C=AC-AB'=AC-AB=2.
在Rt△B'EC中,B'E2+B'C2=CE2,
即x2+22=(4-x)2,
解得x=.
8.解:由题意,知BC=AD=AF=10
cm,DE=EF.
在Rt△ABF中,BF===6(cm),
∴CF=BC-BF=4
cm.
设CE=x
cm,则DE=EF=(8-x)cm.
在Rt△FEC中,由勾股定理,
得CF2+CE2=EF2,即42+x2=(8-x)2,
解得x=3,即CE=3
cm.
9.> 解析:
∵∠C=90°,BC=3,BD=AC=1,∴CD=2,AB==,
∴AD==,
∴AD+BD=+1.
又∵△ABD中,AD+BD>AB,
∴+1>.
10.0,
11.解:如图:
利用勾股定理,得AC==5,BC==,AB=2-(-3)=5,
∴△ABC的周长为AC+BC+AB=5++5=10+,△ABC的面积为×5×3=.
12.解:(1)如图①所示.
(2)如图②所示.
(3)如图③所示.
(4)如图④所示.
13.解:(1)根据勾股定理,得OA2=,OA3=,OA4=2,…,OA10=,…,OAn=.
S1=,S2=,S3=,…,S10=,…,Sn=.
(2)+++…+=2+2+2+…+2==.
