人教版八年级数学下册课时作业:17.1 第1课时 勾股定理及验证(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学下册课时作业:17.1 第1课时 勾股定理及验证(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 165.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 00:00:00 | ||
图片预览


文档简介
17.1 第1课时 勾股定理及验证
知识点
1 勾股定理的认识及验证
1.已知a,b,c分别是∠A,∠B,∠C的对边,则下列说法中正确的是
( )
A.若a,b,c是△ABC的三边长,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边长,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边长,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边长,∠C=90°,则a2+b2=c2
2.如图,已知两正方形的面积分别是25和169,则字母B所代表的正方形的面积是( )
A.12
B.13
C.144
D.194
3.历史上对勾股定理的一种证明方法采用的图形如图,用四个直角边长分别为a,b,斜边长为c的直角三角形拼成一个大正方形,求图形中央的小正方形的面积.不难得到:
(1)方法一:小正方形的面积为
;?
(2)方法二:小正方形的面积为
;?
(3)由方法一、二,可以得到a,b,c的关系为 .?
知识点
2 利用勾股定理进行计算
4.在直角三角形中,若勾为3,股为4,则弦为
( )
A.5
B.6
C.7
D.8
5.在Rt△ABC中,斜边BC=3,则AB2+AC2的值为
( )
A.18
B.9
C.6
D.无法计算
6.
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)若a=5,b=12,则c= ;?
(2)若a=8,b=15,则c= ;?
(3)若c=25,b=20,则a= ;?
(4)若∠A=30°,a=,则b= ,c= ;?
(5)若∠A=45°,c=6,则a= ,b= ;?
(6)若a∶b=1∶2,c=2,则a= ,b= .?
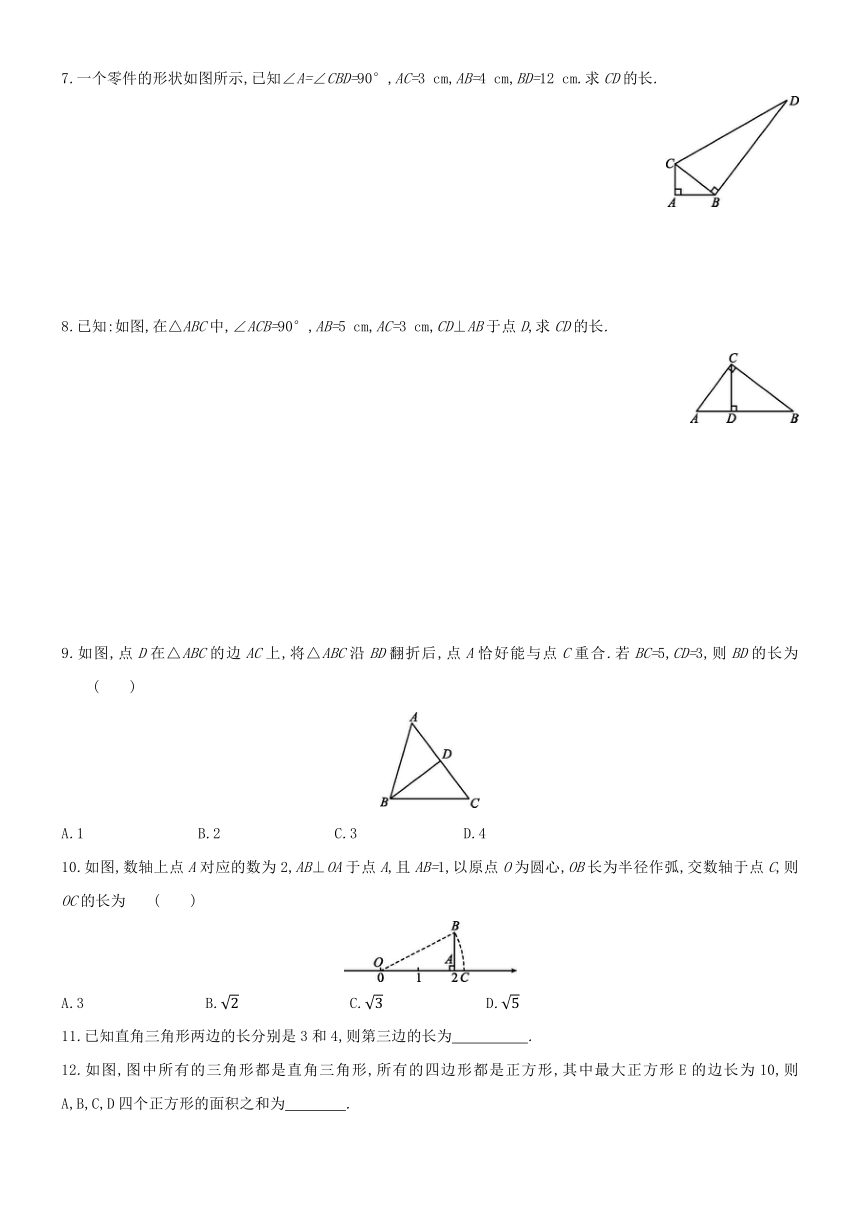
7.一个零件的形状如图所示,已知∠A=∠CBD=90°,AC=3
cm,AB=4
cm,BD=12
cm.求CD的长.
8.已知:如图,在△ABC中,∠ACB=90°,AB=5
cm,AC=3
cm,CD⊥AB于点D,求CD的长.
9.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好能与点C重合.若BC=5,CD=3,则BD的长为
( )
A.1
B.2
C.3
D.4
10.如图,数轴上点A对应的数为2,AB⊥OA于点A,且AB=1,以原点O为圆心,OB长为半径作弧,交数轴于点C,则OC的长为
( )
A.3
B.
C.
D.
11.已知直角三角形两边的长分别是3和4,则第三边的长为 .?
12.如图,图中所有的三角形都是直角三角形,所有的四边形都是正方形,其中最大正方形E的边长为10,则A,B,C,D四个正方形的面积之和为 .?
13.如图,在四边形ABCD中,∠B=∠D=90°,AB=BC=2,CD=1,求AD的长.
14.如图,在四边形BCDE中,∠C=∠BED=90°,∠B=60°,延长CD,BE,两线相交于点A,已知CD=2,DE=1,求Rt△ABC的面积.
15.如图,在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.
(1)若a∶b=5∶12,c=26,求△ABC的周长;
(2)若∠A=30°,b=2,求斜边AB上的高.
16.据图回答问题:
(1)请你根据图①中的直角三角形叙述勾股定理(用符号语言叙述);
(2)以图①中的直角三角形为基础,可以构造出以a,b为底,以a+b为高的直角梯形,如图②,利用图②证明勾股定理;
(3)运用勾股定理解决以下问题:如图③,在△ABC中,AB=2,AC=3,∠B=45°,则BC= .?
答案
1.D 解析:
对于选项A,因为只有在直角三角形的前提下才能使用勾股定理,所以A项不正确.对于选项B,因为不知道哪一条边是斜边,所以B项不正确.对于选项C,因为∠A=90°,所以a是斜边长,故应有b2+c2=a2,所以C项不正确.只有选项D符合勾股定理的内容.故选D.
2.C
3.(1)c2-4×ab (2)(b-a)2
(3)a2+b2=c2
4.A
5.B
6.(1)13 (2)17 (3)15 (4)3 2
(5)3 3 (6)2 4
7.解:在Rt△ABC中,根据勾股定理,得
BC2=AB2+AC2=42+32=25.
在Rt△CBD中,根据勾股定理,得CD2=BC2+BD2=25+122=169,
所以CD==13,
即CD的长为13
cm.
8.解:∵∠ACB=90°,AB=5
cm,AC=3
cm,
∴BC===4(cm).
∵CD⊥AB,
∴S△ABC=AC·BC=AB·CD,
即×3×4=×5·CD,
解得CD=
cm.
9.D 解析:
由翻折可得∠BDC=90°,根据勾股定理可得BD===4.
10.D 解析:
∵AB⊥OA于点A,∴∠OAB=90°.在Rt△OAB中,由勾股定理得OB===,∴OC=OB=.故选D.
11.5或 解析:
若3,4为两直角边长,则第三边是斜边,其长为5;若长为4的边是斜边,则第三边是直角边,其长为.故第三边长为5或.
12.100
13.解:连接AC,如图.
∵∠B=90°,
∴△ABC为直角三角形,
∴AC2=AB2+BC2.
∵AB=BC=2,
∴AC2=8.
∵∠D=90°,
∴△ADC为直角三角形.
∵CD=1,
∴AD2=AC2-CD2=7,
∴AD=.
14.解:∵∠C=90°,∠B=60°,
∴∠A=30°,
∴AD=2DE=2,AB=2BC,
∴AC=AD+CD=4.
设BC=x,则AB=2x.
由勾股定理得AB2-BC2=AC2,
即(2x)2-x2=16,
解得x=(负值已舍去),即BC=,
则Rt△ABC的面积为BC·AC=.
15.解:(1)∵a∶b=5∶12,
∴设a=5x,则b=12x.
∵在Rt△ABC中,∠C=90°,∴a2+b2=c2,
即(5x)2+(12x)2=262,解得x=2(负值已舍去),
∴a=10,b=24,
∴△ABC的周长为a+b+c=10+24+26=60.
(2)在Rt△ABC中,
∵∠A=30°,∠C=90°,
∴c=2a,
∴a2+b2=c2=4a2.
∵b=2,∴a=2,c=4.
过点C作CD⊥AB于点D.
∵S△ABC=AB·CD=AC·BC,
∴CD===,
即斜边AB上的高为.
16.解:(1)如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
(2)证明:∵Rt△ABE≌Rt△ECD,
∴∠AEB=∠EDC.
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠DEC=90°,
∴∠AED=90°.
∵梯形ABCD的面积=Rt△ABE的面积+Rt△DEC的面积+Rt△AED的面积,
∴(a+b)(a+b)=ab+ab+c2,
整理,得a2+b2=c2.
(3)如图,过点A作AD⊥BC于点D.
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
∵在Rt△ABD中,∠B=45°,∴AD=BD.
∵AB=2,∴AD2+BD2=22,
∴AD=BD=.
在Rt△ACD中,CD2=AC2-AD2,
∴CD===4,
∴BC=CD+BD=4+.
故答案为4+.
知识点
1 勾股定理的认识及验证
1.已知a,b,c分别是∠A,∠B,∠C的对边,则下列说法中正确的是
( )
A.若a,b,c是△ABC的三边长,则a2+b2=c2
B.若a,b,c是Rt△ABC的三边长,则a2+b2=c2
C.若a,b,c是Rt△ABC的三边长,∠A=90°,则a2+b2=c2
D.若a,b,c是Rt△ABC的三边长,∠C=90°,则a2+b2=c2
2.如图,已知两正方形的面积分别是25和169,则字母B所代表的正方形的面积是( )
A.12
B.13
C.144
D.194
3.历史上对勾股定理的一种证明方法采用的图形如图,用四个直角边长分别为a,b,斜边长为c的直角三角形拼成一个大正方形,求图形中央的小正方形的面积.不难得到:
(1)方法一:小正方形的面积为
;?
(2)方法二:小正方形的面积为
;?
(3)由方法一、二,可以得到a,b,c的关系为 .?
知识点
2 利用勾股定理进行计算
4.在直角三角形中,若勾为3,股为4,则弦为
( )
A.5
B.6
C.7
D.8
5.在Rt△ABC中,斜边BC=3,则AB2+AC2的值为
( )
A.18
B.9
C.6
D.无法计算
6.
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)若a=5,b=12,则c= ;?
(2)若a=8,b=15,则c= ;?
(3)若c=25,b=20,则a= ;?
(4)若∠A=30°,a=,则b= ,c= ;?
(5)若∠A=45°,c=6,则a= ,b= ;?
(6)若a∶b=1∶2,c=2,则a= ,b= .?
7.一个零件的形状如图所示,已知∠A=∠CBD=90°,AC=3
cm,AB=4
cm,BD=12
cm.求CD的长.
8.已知:如图,在△ABC中,∠ACB=90°,AB=5
cm,AC=3
cm,CD⊥AB于点D,求CD的长.
9.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好能与点C重合.若BC=5,CD=3,则BD的长为
( )
A.1
B.2
C.3
D.4
10.如图,数轴上点A对应的数为2,AB⊥OA于点A,且AB=1,以原点O为圆心,OB长为半径作弧,交数轴于点C,则OC的长为
( )
A.3
B.
C.
D.
11.已知直角三角形两边的长分别是3和4,则第三边的长为 .?
12.如图,图中所有的三角形都是直角三角形,所有的四边形都是正方形,其中最大正方形E的边长为10,则A,B,C,D四个正方形的面积之和为 .?
13.如图,在四边形ABCD中,∠B=∠D=90°,AB=BC=2,CD=1,求AD的长.
14.如图,在四边形BCDE中,∠C=∠BED=90°,∠B=60°,延长CD,BE,两线相交于点A,已知CD=2,DE=1,求Rt△ABC的面积.
15.如图,在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b.
(1)若a∶b=5∶12,c=26,求△ABC的周长;
(2)若∠A=30°,b=2,求斜边AB上的高.
16.据图回答问题:
(1)请你根据图①中的直角三角形叙述勾股定理(用符号语言叙述);
(2)以图①中的直角三角形为基础,可以构造出以a,b为底,以a+b为高的直角梯形,如图②,利用图②证明勾股定理;
(3)运用勾股定理解决以下问题:如图③,在△ABC中,AB=2,AC=3,∠B=45°,则BC= .?
答案
1.D 解析:
对于选项A,因为只有在直角三角形的前提下才能使用勾股定理,所以A项不正确.对于选项B,因为不知道哪一条边是斜边,所以B项不正确.对于选项C,因为∠A=90°,所以a是斜边长,故应有b2+c2=a2,所以C项不正确.只有选项D符合勾股定理的内容.故选D.
2.C
3.(1)c2-4×ab (2)(b-a)2
(3)a2+b2=c2
4.A
5.B
6.(1)13 (2)17 (3)15 (4)3 2
(5)3 3 (6)2 4
7.解:在Rt△ABC中,根据勾股定理,得
BC2=AB2+AC2=42+32=25.
在Rt△CBD中,根据勾股定理,得CD2=BC2+BD2=25+122=169,
所以CD==13,
即CD的长为13
cm.
8.解:∵∠ACB=90°,AB=5
cm,AC=3
cm,
∴BC===4(cm).
∵CD⊥AB,
∴S△ABC=AC·BC=AB·CD,
即×3×4=×5·CD,
解得CD=
cm.
9.D 解析:
由翻折可得∠BDC=90°,根据勾股定理可得BD===4.
10.D 解析:
∵AB⊥OA于点A,∴∠OAB=90°.在Rt△OAB中,由勾股定理得OB===,∴OC=OB=.故选D.
11.5或 解析:
若3,4为两直角边长,则第三边是斜边,其长为5;若长为4的边是斜边,则第三边是直角边,其长为.故第三边长为5或.
12.100
13.解:连接AC,如图.
∵∠B=90°,
∴△ABC为直角三角形,
∴AC2=AB2+BC2.
∵AB=BC=2,
∴AC2=8.
∵∠D=90°,
∴△ADC为直角三角形.
∵CD=1,
∴AD2=AC2-CD2=7,
∴AD=.
14.解:∵∠C=90°,∠B=60°,
∴∠A=30°,
∴AD=2DE=2,AB=2BC,
∴AC=AD+CD=4.
设BC=x,则AB=2x.
由勾股定理得AB2-BC2=AC2,
即(2x)2-x2=16,
解得x=(负值已舍去),即BC=,
则Rt△ABC的面积为BC·AC=.
15.解:(1)∵a∶b=5∶12,
∴设a=5x,则b=12x.
∵在Rt△ABC中,∠C=90°,∴a2+b2=c2,
即(5x)2+(12x)2=262,解得x=2(负值已舍去),
∴a=10,b=24,
∴△ABC的周长为a+b+c=10+24+26=60.
(2)在Rt△ABC中,
∵∠A=30°,∠C=90°,
∴c=2a,
∴a2+b2=c2=4a2.
∵b=2,∴a=2,c=4.
过点C作CD⊥AB于点D.
∵S△ABC=AB·CD=AC·BC,
∴CD===,
即斜边AB上的高为.
16.解:(1)如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
(2)证明:∵Rt△ABE≌Rt△ECD,
∴∠AEB=∠EDC.
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠DEC=90°,
∴∠AED=90°.
∵梯形ABCD的面积=Rt△ABE的面积+Rt△DEC的面积+Rt△AED的面积,
∴(a+b)(a+b)=ab+ab+c2,
整理,得a2+b2=c2.
(3)如图,过点A作AD⊥BC于点D.
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
∵在Rt△ABD中,∠B=45°,∴AD=BD.
∵AB=2,∴AD2+BD2=22,
∴AD=BD=.
在Rt△ACD中,CD2=AC2-AD2,
∴CD===4,
∴BC=CD+BD=4+.
故答案为4+.
