人教版八年级数学下册课时作业:17.2 第2课时 勾股定理及其逆定理的综合应用(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学下册课时作业:17.2 第2课时 勾股定理及其逆定理的综合应用(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 217.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 00:00:00 | ||
图片预览


文档简介
第2课时 勾股定理及其逆定理的综合应用
知识点
1 勾股定理的逆定理的应用
1.有五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,其中正确的是( )
2.一位工人师傅测量一个等腰三角形工件的腰、底及底边上的高,并按顺序记录下数据,量完后,不小心与记录的其他几组数据混淆了,则下列数据中是这个等腰三角形工件的数据的是( )
A.13,10,10
B.13,10,12
C.13,12,12
D.13,10,11
3.一根电线杆高12
m,为了安全起见,在电线杆顶部到与电线杆底部水平距离5
m处加一根拉线,拉线工人发现所用线长为13.2米(不计捆缚部分),则电线杆与地面 .(填“垂直”或“不垂直”)?
4.如图,正方形网格中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上.
(1)分别求出AB,BC,AC的长;
(2)试判断△ABC的形状,并说明理由.
知识点
2 勾股定理及其逆定理的综合应用
5.如图,每个小正方形的边长均为1,A,B,C均为小正方形的顶点,则∠ABC的度数为( )
A.90°
B.60°
C.45°
D.30°
6.如图,在△ABC中,D为BC上一点,且BD=3,CD=AB=5,AD=4,则AC= .?
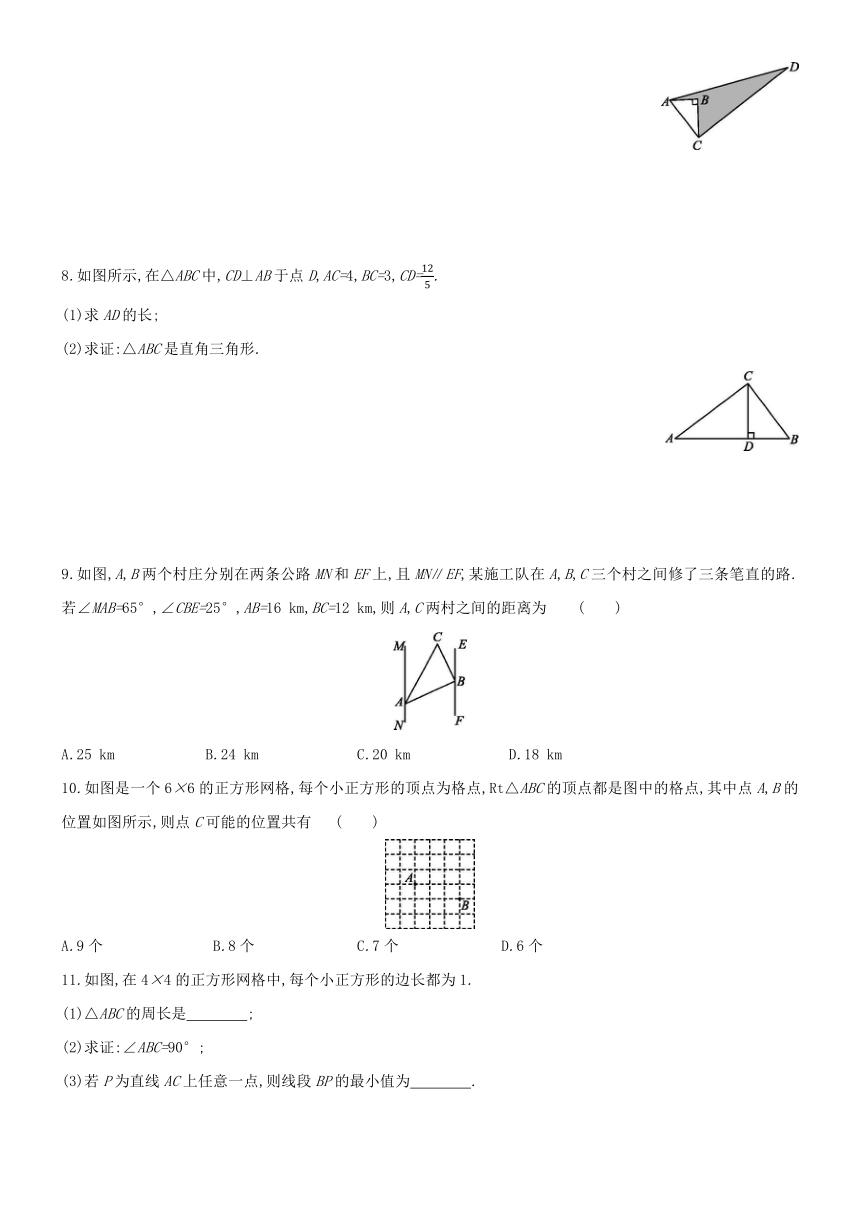
7.如图,在△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13,求阴影部分的面积.
8.如图所示,在△ABC中,CD⊥AB于点D,AC=4,BC=3,CD=.
(1)求AD的长;
(2)求证:△ABC是直角三角形.
9.如图,A,B两个村庄分别在两条公路MN和EF上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=16
km,BC=12
km,则A,C两村之间的距离为
( )
A.25
km
B.24
km
C.20
km
D.18
km
10.如图是一个6×6的正方形网格,每个小正方形的顶点为格点,Rt△ABC的顶点都是图中的格点,其中点A,B的位置如图所示,则点C可能的位置共有
( )
A.9个
B.8个
C.7个
D.6个
11.如图,在4×4的正方形网格中,每个小正方形的边长都为1.
(1)△ABC的周长是 ;?
(2)求证:∠ABC=90°;
(3)若P为直线AC上任意一点,则线段BP的最小值为 .?
12.如图,在△ABC中,AB=3,AC=5,BC边上的中线DA=2,延长AD到点E,使DE=DA,连接CE.
(1)求证:△DEC≌△DAB;
(2)求证:CE⊥AE;
(3)求BC边的长.
13.张老师在一次“探究性学习”课中,设计了如下数表:
n
2
3
4
5
…
a
22-1
32-1
42-1
52-1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a= ,b= ,c= .?
(2)猜想:以a,b,c为三边长的三角形是不是直角三角形?为什么?
答案
1.C 解析:
A项,72+242=252,152+242≠202,故不正确.B项,72+242=252,152+202≠242,故不正确.C项,72+242=252,152+202=252,故正确.D项,72+202≠252,242+152≠252,故不正确.
2.B
3.不垂直
4.解:(1)AB==,BC==2,AC==5.
(2)△ABC是直角三角形.理由如下:
∵AB2+BC2=()2+(2)2=25,AC2=52=25,
∴AB2+BC2=AC2,
∴△ABC是直角三角形.
5.C
6. 解析:
∵BD=3,AB=5,AD=4,
∴BD2+AD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°,
∴∠ADC=90°,
∴△ACD是直角三角形.
又∵AD=4,CD=5,
∴AC==.
7.解:在Rt△ABC中,∵∠B=90°,AB=3,BC=4,
∴AC==5.
又∵CD=12,AD=13,
∴AC2+CD2=52+122=169,AD2=132=169,
∴AD2=AC2+CD2,
∴∠ACD=90°,
∴S阴影=S△ACD-S△ABC=AC·CD-AB·BC=×5×12-×3×4=24.
8.解:(1)∵CD⊥AB,∴∠ADC=90°,
∴AD===.
(2)证明:∵CD⊥AB,∴∠CDB=90°,
∴BD===.
又∵AD=,∴AB=AD+BD=5.
∵32+42=52,∴BC2+AC2=AB2,
∴△ABC是直角三角形.
9.C 解析:
∵MN∥EF,∠MAB=65°,
∴∠ABF=65°.
∵∠CBE=25°,
∴∠ABC=180°-65°-25°=90°,
∴△ABC是直角三角形,
∴AC===20(km).
10.A 解析:
如图所示,共9个点.
11.解:(1)3+5
(2)证明:由勾股定理,得AB==2,
BC==,AC==5,
∴AB2+BC2=+()2=25=AC2,
∴∠ABC=90°.
(3)易知当BP⊥AC时,BP的长最小,
此时S△ABC=BC·AB=AC·BP,
∴BP==2,即BP的最小值是2.
12.解:(1)证明:∵DA是BC边上的中线,
∴DC=DB.
在△DEC和△DAB中,
∴△DEC≌△DAB.
(2)证明:由(1)知△DEC≌△DAB,
∴CE=AB=3.
∵DA=2,DE=DA,∴AE=4.
在△AEC中,
∵AE2+CE2=42+32=25,AC2=52=25,
∴AE2+CE2=AC2,
∴∠E=90°,即CE⊥AE.
(3)在Rt△DEC中,DC==,故BC=2DC=2.
13.解:(1)n2-1 2n n2+1
(2)以a,b,c为三边长的三角形是直角三角形.
理由:∵a2+b2=(n2-1)2+(2n)2=n4+2n2+1,
c2=(n2+1)2=n4+2n2+1,
∴a2+b2=c2,
∴以a,b,c为三边长的三角形是直角三角形.
知识点
1 勾股定理的逆定理的应用
1.有五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,其中正确的是( )
2.一位工人师傅测量一个等腰三角形工件的腰、底及底边上的高,并按顺序记录下数据,量完后,不小心与记录的其他几组数据混淆了,则下列数据中是这个等腰三角形工件的数据的是( )
A.13,10,10
B.13,10,12
C.13,12,12
D.13,10,11
3.一根电线杆高12
m,为了安全起见,在电线杆顶部到与电线杆底部水平距离5
m处加一根拉线,拉线工人发现所用线长为13.2米(不计捆缚部分),则电线杆与地面 .(填“垂直”或“不垂直”)?
4.如图,正方形网格中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上.
(1)分别求出AB,BC,AC的长;
(2)试判断△ABC的形状,并说明理由.
知识点
2 勾股定理及其逆定理的综合应用
5.如图,每个小正方形的边长均为1,A,B,C均为小正方形的顶点,则∠ABC的度数为( )
A.90°
B.60°
C.45°
D.30°
6.如图,在△ABC中,D为BC上一点,且BD=3,CD=AB=5,AD=4,则AC= .?
7.如图,在△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13,求阴影部分的面积.
8.如图所示,在△ABC中,CD⊥AB于点D,AC=4,BC=3,CD=.
(1)求AD的长;
(2)求证:△ABC是直角三角形.
9.如图,A,B两个村庄分别在两条公路MN和EF上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=16
km,BC=12
km,则A,C两村之间的距离为
( )
A.25
km
B.24
km
C.20
km
D.18
km
10.如图是一个6×6的正方形网格,每个小正方形的顶点为格点,Rt△ABC的顶点都是图中的格点,其中点A,B的位置如图所示,则点C可能的位置共有
( )
A.9个
B.8个
C.7个
D.6个
11.如图,在4×4的正方形网格中,每个小正方形的边长都为1.
(1)△ABC的周长是 ;?
(2)求证:∠ABC=90°;
(3)若P为直线AC上任意一点,则线段BP的最小值为 .?
12.如图,在△ABC中,AB=3,AC=5,BC边上的中线DA=2,延长AD到点E,使DE=DA,连接CE.
(1)求证:△DEC≌△DAB;
(2)求证:CE⊥AE;
(3)求BC边的长.
13.张老师在一次“探究性学习”课中,设计了如下数表:
n
2
3
4
5
…
a
22-1
32-1
42-1
52-1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a= ,b= ,c= .?
(2)猜想:以a,b,c为三边长的三角形是不是直角三角形?为什么?
答案
1.C 解析:
A项,72+242=252,152+242≠202,故不正确.B项,72+242=252,152+202≠242,故不正确.C项,72+242=252,152+202=252,故正确.D项,72+202≠252,242+152≠252,故不正确.
2.B
3.不垂直
4.解:(1)AB==,BC==2,AC==5.
(2)△ABC是直角三角形.理由如下:
∵AB2+BC2=()2+(2)2=25,AC2=52=25,
∴AB2+BC2=AC2,
∴△ABC是直角三角形.
5.C
6. 解析:
∵BD=3,AB=5,AD=4,
∴BD2+AD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°,
∴∠ADC=90°,
∴△ACD是直角三角形.
又∵AD=4,CD=5,
∴AC==.
7.解:在Rt△ABC中,∵∠B=90°,AB=3,BC=4,
∴AC==5.
又∵CD=12,AD=13,
∴AC2+CD2=52+122=169,AD2=132=169,
∴AD2=AC2+CD2,
∴∠ACD=90°,
∴S阴影=S△ACD-S△ABC=AC·CD-AB·BC=×5×12-×3×4=24.
8.解:(1)∵CD⊥AB,∴∠ADC=90°,
∴AD===.
(2)证明:∵CD⊥AB,∴∠CDB=90°,
∴BD===.
又∵AD=,∴AB=AD+BD=5.
∵32+42=52,∴BC2+AC2=AB2,
∴△ABC是直角三角形.
9.C 解析:
∵MN∥EF,∠MAB=65°,
∴∠ABF=65°.
∵∠CBE=25°,
∴∠ABC=180°-65°-25°=90°,
∴△ABC是直角三角形,
∴AC===20(km).
10.A 解析:
如图所示,共9个点.
11.解:(1)3+5
(2)证明:由勾股定理,得AB==2,
BC==,AC==5,
∴AB2+BC2=+()2=25=AC2,
∴∠ABC=90°.
(3)易知当BP⊥AC时,BP的长最小,
此时S△ABC=BC·AB=AC·BP,
∴BP==2,即BP的最小值是2.
12.解:(1)证明:∵DA是BC边上的中线,
∴DC=DB.
在△DEC和△DAB中,
∴△DEC≌△DAB.
(2)证明:由(1)知△DEC≌△DAB,
∴CE=AB=3.
∵DA=2,DE=DA,∴AE=4.
在△AEC中,
∵AE2+CE2=42+32=25,AC2=52=25,
∴AE2+CE2=AC2,
∴∠E=90°,即CE⊥AE.
(3)在Rt△DEC中,DC==,故BC=2DC=2.
13.解:(1)n2-1 2n n2+1
(2)以a,b,c为三边长的三角形是直角三角形.
理由:∵a2+b2=(n2-1)2+(2n)2=n4+2n2+1,
c2=(n2+1)2=n4+2n2+1,
∴a2+b2=c2,
∴以a,b,c为三边长的三角形是直角三角形.
