人教版 九年级数学下册 第27章 相似 突破训练(Word版 含答案)
文档属性
| 名称 | 人教版 九年级数学下册 第27章 相似 突破训练(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 449.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 00:00:00 | ||
图片预览



文档简介
人教版 九年级数学下册 第27章 相似 突破训练
一、选择题
1. (2019?雅安)若,且,则的值是
A.4 B.2
C.20 D.14
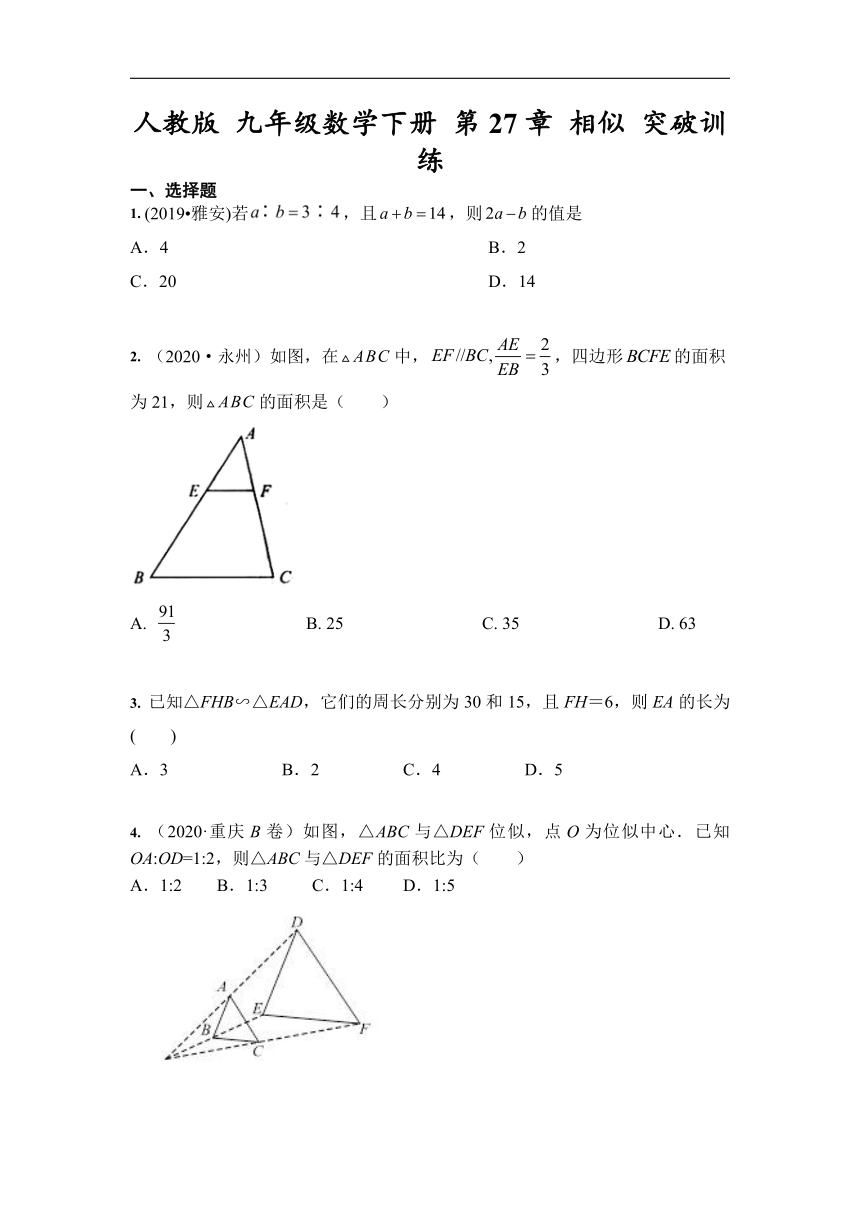
2. (2020·永州)如图,在中,,四边形的面积为21,则的面积是( )
A. B. 25 C. 35 D. 63
3. 已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( )
A.3 B.2 C.4 D.5
4. (2020·重庆B卷)如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
5. (2020·重庆A卷)如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),C(3,1),以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,则线段DF的长度为( )
A. B. C. D.
6. (2020·哈尔滨)如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )
A. B. C. D.
7. (2020·嘉兴) 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点C坐标为( )
A.(﹣1,﹣1) B.() C.() D.(﹣2,﹣1)
8. 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( )
A. 1 B. 2 C. 3 D. 4
二、填空题
9. (2020·南通)如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上,设△ABC的周长为C1,△DEF的周长为C2,则的值等于 ▲ .
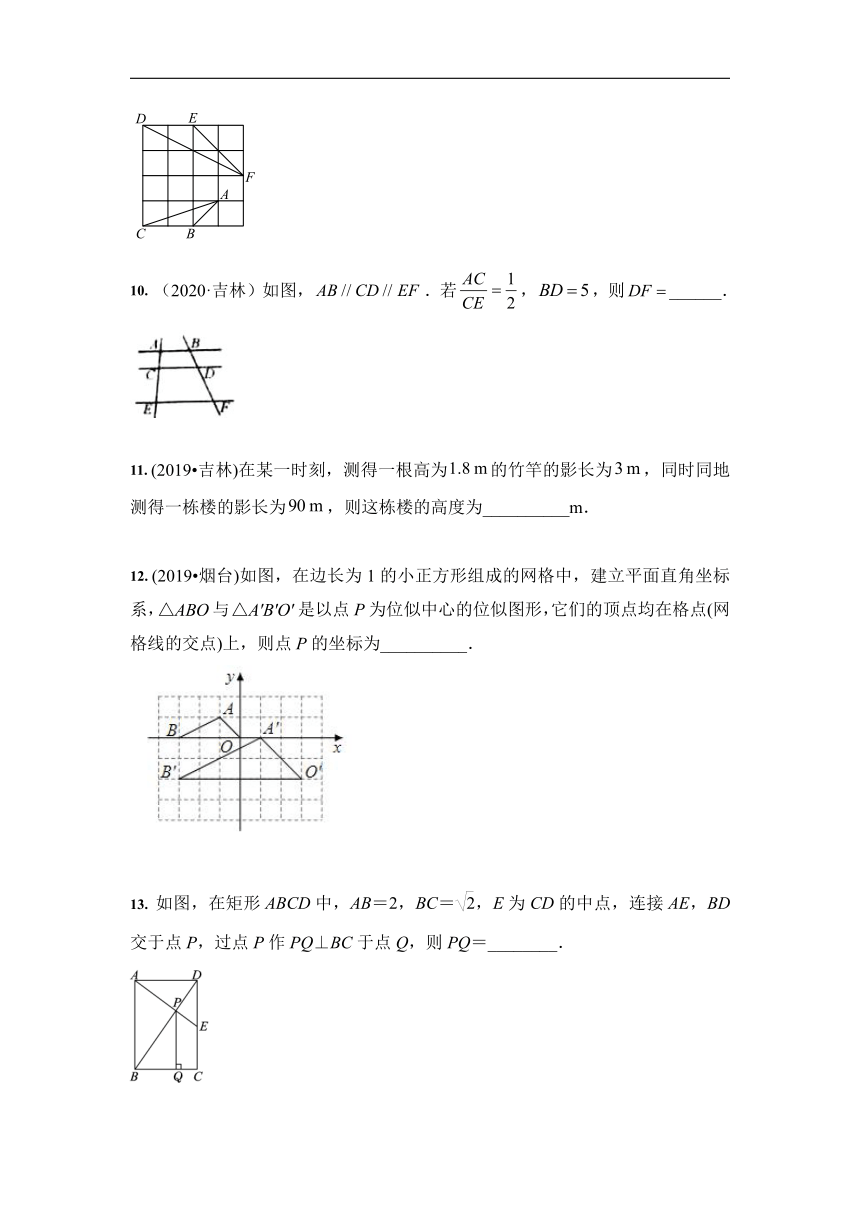
10. (2020·吉林)如图,.若,,则______.
11. (2019?吉林)在某一时刻,测得一根高为的竹竿的影长为,同时同地测得一栋楼的影长为,则这栋楼的高度为__________m.
12. (2019?烟台)如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,与是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为__________.
13. 如图,在矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE,BD交于点P,过点P作PQ⊥BC于点Q,则PQ=________.
14. (2020·绥化)在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(2,4),则其对应点A1的坐标是______.
三、解答题
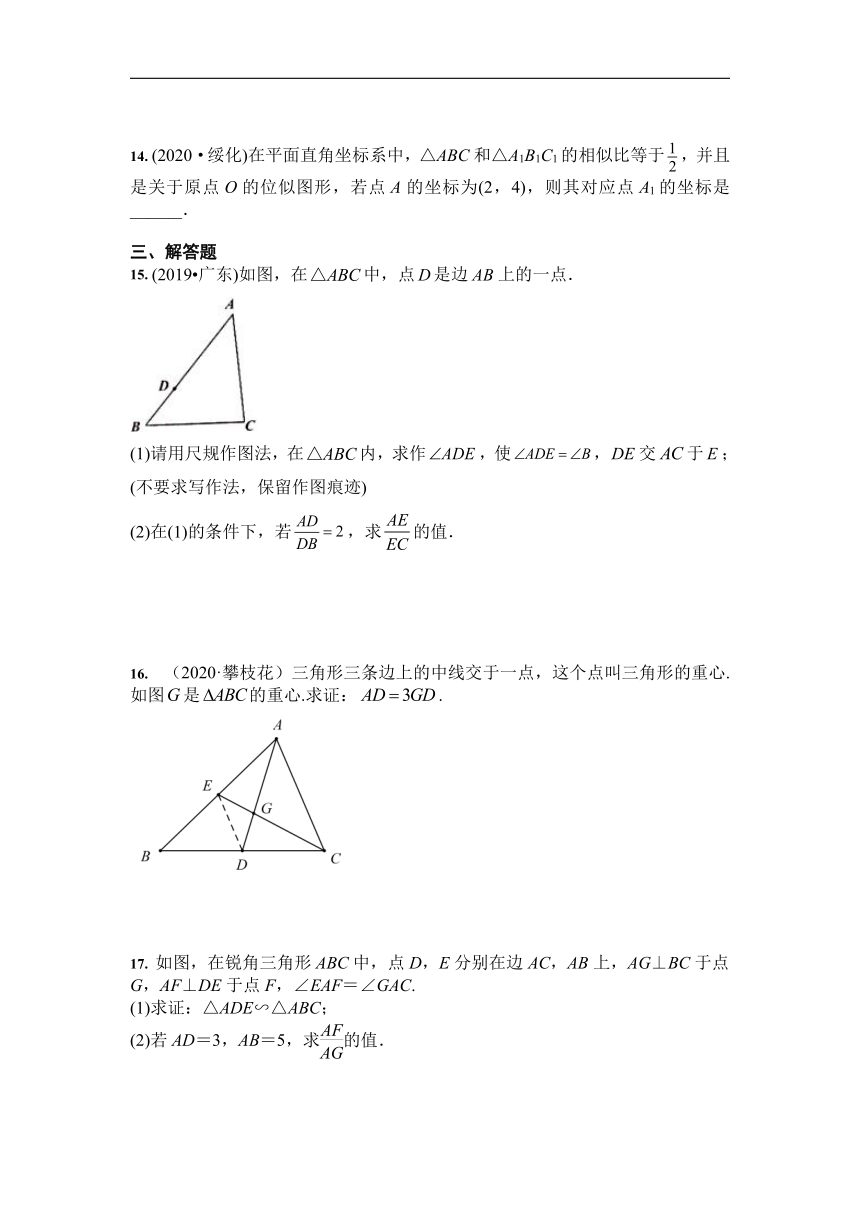
15. (2019?广东)如图,在中,点是边上的一点.
(1)请用尺规作图法,在内,求作,使,交于;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,若,求的值.
16. (2020·攀枝花)三角形三条边上的中线交于一点,这个点叫三角形的重心.如图是的重心.求证:.
17. 如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求的值.
18. 如图,已知AB是⊙O的直径,C是⊙O上的一点,D是AB上的一点,DE⊥AB于点D,DE交BC于点F,且EF=EC.
(1)求证:EC是⊙O的切线;
(2)若BD=4,BC=8,⊙O的半径OB=5,求EC的长.
人教版 九年级数学下册 第27章 相似 突破训练-答案
一、选择题
1. 【答案】A
【解析】由a∶b=3∶4知,所以.
所以由得到:,
解得.所以.
所以.故选A.
2. 【答案】B
【详解】解:∵
∴
∴
∵
∴
∴
∴
∵
∴
∴
故选:B.
3. 【答案】A
4. 【答案】C
【解析】本题考查了相似三角形的性质, ∵△ABC与△DEF位似,且,∴,因此本题选C.
5. 【答案】D
【解析】∵A(1,2),B(1,1),C(3,1),∴AB=1,BC=2,AC=.∵△DEF与△ABC成位似图形,且相似比为2,∴DF=2AB=2.
6. 【答案】C【解析】本题考查了平行线分线段成比例和由平行判定相似,∵EF∥BC,∴,∵EF∥BC,∴,∴因此本题选C.
7. 【答案】B
【解析】本题考查了在坐标系中,位似图形点的坐标.在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(–kx,–ky).由A(4,3),位似比k=,可得C()因此本题选B.
8. 【答案】A 【解析】∵AD是∠BAC的平分线,AC⊥BC,AE⊥DE, ∴DC=DE,AE=AC.又∵DE是AB的垂直平分线,∴BE=AE,即AB=2AE=2AC, ∴∠B=30°.设DE=x,则BD=3-x.在Rt△BDE中,=,解得x=1,∴DE的长为1.
二、填空题
9. 【答案】
【解析】由图形易证△ABC与△DEF相似,且相似比为,所以周长比为.故答案为:.
10. 【答案】10
【解析】∵,∴,
又∵,,∴,∴,故答案为:10.
11. 【答案】54
【解析】设这栋楼的高度为h m,
∵在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时测得一栋楼的影长为60 m,
∴,解得h=54(m).故答案为:54.
12. 【答案】
【解析】如图,连接并延长,并延长,与的交点即为位似中心P点,
由图可知、B、P在一条直线上,则P点横坐标为–3,
由图可得和的位似比为,,
所以,解得PB=2,
所以P点纵坐标为2,即P点坐标为.故答案为:.
13. 【答案】 [解析] ∵四边形ABCD是矩形,
∴AB∥CD,AB=CD.
∵E为CD的中点,∴DE=CD=AB=1.
∵AB∥CD,∴△ABP∽△EDP,∴=,∴=,∴=.
∵PQ⊥BC,∴PQ∥CD,
∴△BPQ∽△BDC,∴==.
∵CD=2,∴PQ=.
14. 【答案】(-4,-8)或(4,8)
【解析】∵△ABC和△A1B1C1的相似比等于,∴△A1B1C1和△ABC的相似比等于2.因此将点A(2,4)的横、纵坐标乘以±2即得点A1的坐标,∴点A1的坐标是(-4,-8)或(4,8).
三、解答题
15. 【答案】
(1)如图所示:
(2)∵,
∴.
∴.
16. 【答案】
证明:连接DE,
∵点G是△ABC的重心,
∴点E和点D分别是AB和BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC且DE=AC,
∴△DEG∽△ACG,
∴,
∴
∴AD=3DG,
即AD=3GD.
17. 【答案】
【思维教练】(1)要证△ADE∽△ABC,现已知∠EAD=∠CAB,故只需找另一组对角相等或夹角的两边对应成比例.由题干条件易知∠EAF=∠GAC,∠AFE=∠AGC,故△AEF∽△ACG,∠AEF=∠C,由两角对应相等即可得证;(2)由(1)中的结论,利用相似三角形的性质求解即可.
(1)证明:在△ABC中,∵AG⊥BC于点G,AF⊥DE于点F,
∴∠AFE=∠AGC=90°,
在△AEF和△ACG中,
∵∠AFE=∠AGC,∠EAF=∠GAC,
∴△AEF∽△ACG,∴∠AEF=∠C.(2分)
在△ADE和△ABC中,
∵∠AED=∠C,∠EAD=∠CAB,
∴△ADE∽△ABC;(4分)
(2)解:由(1)知△ADE∽△ABC,
∴==,(6分)
又∵△AEF∽△ACG,∴==.(8分)
18. 【答案】
解:(1)证明:如图,连接OC.∵OC=OB,
∴∠OBC=∠OCB.
∵DE⊥AB,
∴∠OBC+∠DFB=90°.
∵EF=EC,∴∠ECF=∠EFC=∠DFB,
∴∠OCB+∠ECF=90°,∴OC⊥CE.
又∵OC是⊙O的半径,
∴EC是⊙O的切线.
(2)∵AB是⊙O的直径,∴∠ACB=90°.
∵OB=5,∴AB=10,∴AC==6.
∵∠ACB=90°,DE⊥AB,∴∠ACB=∠FDB.
又∵∠ABC=∠FBD,∴△ABC∽△FBD,
∴=,∴=,
∴BF=5,∴CF=BC-BF=3.
∵∠ACO+∠OCB=90°,∠OCB+∠FCE=90°,
∴∠ACO=∠FCE.
∵OA=OC,∴∠ACO=∠CAO.
∵∠FCE=∠EFC,
∴∠ACO=∠FCE=∠CAO=∠EFC,
∴△OAC∽△ECF,∴=,
∴EC===.
一、选择题
1. (2019?雅安)若,且,则的值是
A.4 B.2
C.20 D.14
2. (2020·永州)如图,在中,,四边形的面积为21,则的面积是( )
A. B. 25 C. 35 D. 63
3. 已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( )
A.3 B.2 C.4 D.5
4. (2020·重庆B卷)如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
5. (2020·重庆A卷)如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),C(3,1),以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,则线段DF的长度为( )
A. B. C. D.
6. (2020·哈尔滨)如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )
A. B. C. D.
7. (2020·嘉兴) 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点C坐标为( )
A.(﹣1,﹣1) B.() C.() D.(﹣2,﹣1)
8. 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( )
A. 1 B. 2 C. 3 D. 4
二、填空题
9. (2020·南通)如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上,设△ABC的周长为C1,△DEF的周长为C2,则的值等于 ▲ .
10. (2020·吉林)如图,.若,,则______.
11. (2019?吉林)在某一时刻,测得一根高为的竹竿的影长为,同时同地测得一栋楼的影长为,则这栋楼的高度为__________m.
12. (2019?烟台)如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,与是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为__________.
13. 如图,在矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE,BD交于点P,过点P作PQ⊥BC于点Q,则PQ=________.
14. (2020·绥化)在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(2,4),则其对应点A1的坐标是______.
三、解答题
15. (2019?广东)如图,在中,点是边上的一点.
(1)请用尺规作图法,在内,求作,使,交于;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,若,求的值.
16. (2020·攀枝花)三角形三条边上的中线交于一点,这个点叫三角形的重心.如图是的重心.求证:.
17. 如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求的值.
18. 如图,已知AB是⊙O的直径,C是⊙O上的一点,D是AB上的一点,DE⊥AB于点D,DE交BC于点F,且EF=EC.
(1)求证:EC是⊙O的切线;
(2)若BD=4,BC=8,⊙O的半径OB=5,求EC的长.
人教版 九年级数学下册 第27章 相似 突破训练-答案
一、选择题
1. 【答案】A
【解析】由a∶b=3∶4知,所以.
所以由得到:,
解得.所以.
所以.故选A.
2. 【答案】B
【详解】解:∵
∴
∴
∵
∴
∴
∴
∵
∴
∴
故选:B.
3. 【答案】A
4. 【答案】C
【解析】本题考查了相似三角形的性质, ∵△ABC与△DEF位似,且,∴,因此本题选C.
5. 【答案】D
【解析】∵A(1,2),B(1,1),C(3,1),∴AB=1,BC=2,AC=.∵△DEF与△ABC成位似图形,且相似比为2,∴DF=2AB=2.
6. 【答案】C【解析】本题考查了平行线分线段成比例和由平行判定相似,∵EF∥BC,∴,∵EF∥BC,∴,∴因此本题选C.
7. 【答案】B
【解析】本题考查了在坐标系中,位似图形点的坐标.在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(–kx,–ky).由A(4,3),位似比k=,可得C()因此本题选B.
8. 【答案】A 【解析】∵AD是∠BAC的平分线,AC⊥BC,AE⊥DE, ∴DC=DE,AE=AC.又∵DE是AB的垂直平分线,∴BE=AE,即AB=2AE=2AC, ∴∠B=30°.设DE=x,则BD=3-x.在Rt△BDE中,=,解得x=1,∴DE的长为1.
二、填空题
9. 【答案】
【解析】由图形易证△ABC与△DEF相似,且相似比为,所以周长比为.故答案为:.
10. 【答案】10
【解析】∵,∴,
又∵,,∴,∴,故答案为:10.
11. 【答案】54
【解析】设这栋楼的高度为h m,
∵在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时测得一栋楼的影长为60 m,
∴,解得h=54(m).故答案为:54.
12. 【答案】
【解析】如图,连接并延长,并延长,与的交点即为位似中心P点,
由图可知、B、P在一条直线上,则P点横坐标为–3,
由图可得和的位似比为,,
所以,解得PB=2,
所以P点纵坐标为2,即P点坐标为.故答案为:.
13. 【答案】 [解析] ∵四边形ABCD是矩形,
∴AB∥CD,AB=CD.
∵E为CD的中点,∴DE=CD=AB=1.
∵AB∥CD,∴△ABP∽△EDP,∴=,∴=,∴=.
∵PQ⊥BC,∴PQ∥CD,
∴△BPQ∽△BDC,∴==.
∵CD=2,∴PQ=.
14. 【答案】(-4,-8)或(4,8)
【解析】∵△ABC和△A1B1C1的相似比等于,∴△A1B1C1和△ABC的相似比等于2.因此将点A(2,4)的横、纵坐标乘以±2即得点A1的坐标,∴点A1的坐标是(-4,-8)或(4,8).
三、解答题
15. 【答案】
(1)如图所示:
(2)∵,
∴.
∴.
16. 【答案】
证明:连接DE,
∵点G是△ABC的重心,
∴点E和点D分别是AB和BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC且DE=AC,
∴△DEG∽△ACG,
∴,
∴
∴AD=3DG,
即AD=3GD.
17. 【答案】
【思维教练】(1)要证△ADE∽△ABC,现已知∠EAD=∠CAB,故只需找另一组对角相等或夹角的两边对应成比例.由题干条件易知∠EAF=∠GAC,∠AFE=∠AGC,故△AEF∽△ACG,∠AEF=∠C,由两角对应相等即可得证;(2)由(1)中的结论,利用相似三角形的性质求解即可.
(1)证明:在△ABC中,∵AG⊥BC于点G,AF⊥DE于点F,
∴∠AFE=∠AGC=90°,
在△AEF和△ACG中,
∵∠AFE=∠AGC,∠EAF=∠GAC,
∴△AEF∽△ACG,∴∠AEF=∠C.(2分)
在△ADE和△ABC中,
∵∠AED=∠C,∠EAD=∠CAB,
∴△ADE∽△ABC;(4分)
(2)解:由(1)知△ADE∽△ABC,
∴==,(6分)
又∵△AEF∽△ACG,∴==.(8分)
18. 【答案】
解:(1)证明:如图,连接OC.∵OC=OB,
∴∠OBC=∠OCB.
∵DE⊥AB,
∴∠OBC+∠DFB=90°.
∵EF=EC,∴∠ECF=∠EFC=∠DFB,
∴∠OCB+∠ECF=90°,∴OC⊥CE.
又∵OC是⊙O的半径,
∴EC是⊙O的切线.
(2)∵AB是⊙O的直径,∴∠ACB=90°.
∵OB=5,∴AB=10,∴AC==6.
∵∠ACB=90°,DE⊥AB,∴∠ACB=∠FDB.
又∵∠ABC=∠FBD,∴△ABC∽△FBD,
∴=,∴=,
∴BF=5,∴CF=BC-BF=3.
∵∠ACO+∠OCB=90°,∠OCB+∠FCE=90°,
∴∠ACO=∠FCE.
∵OA=OC,∴∠ACO=∠CAO.
∵∠FCE=∠EFC,
∴∠ACO=∠FCE=∠CAO=∠EFC,
∴△OAC∽△ECF,∴=,
∴EC===.
