鲁教版(五四制)数学八年级上册第三章-数据的分析 复习检测(word版含答案)
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册第三章-数据的分析 复习检测(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 50.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 20:34:10 | ||
图片预览

文档简介
鲁教版数学八年级上册第三章-数据的分析
复习检测
一、选择题
一组数据0、、3、2、1的极差是
A.
4
B.
3
C.
2
D.
1
下列命题为真命题的是
A.
若,则
B.
等角的余角相等
C.
同旁内角相等,两直线平行
D.
,,则A组数据更稳定
数据1,2,3,4,5,的平均数是
A.
2
B.
3
C.
4
D.
5
一组数据2,4,3,5,2的中位数是
A.
5
B.
C.
3
D.
甲、乙、丙、丁四位同学五次数学测验成绩统计如表所示,如果从这四位同学中,选出一位同学参加数学竞赛.那么应选谁去.
甲
乙
丙
丁
平均分
85
90
90
85
方差
50
42
50
42
A.
甲
B.
乙
C.
丙
D.
丁
甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均数都是环,方差分别是,,,,则射箭成绩最稳定的是
A.
甲
B.
乙
C.
丙
D.
丁
今年3月12日,某学校开展植树活动,某植树小组20名同学的年龄情况如下表:
?年龄岁
?12
?13
?14
?15
?16
?人数
?1
?4
?3
?5
?7
则这20名同学年龄的众数和中位数分别是
A.
15,14
B.
15,15
C.
16,14
D.
16,15
10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是
A.
B.
C.
D.
为评估一种农作物的种植效果,选了8块地作试验田,这8块地的亩产量单位:分别为,,,,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是
A.
,,,的平均数
B.
,,,的方差
C.
,,,的中位数
D.
,,,的众数
某公司全体职工的月工资如下:
月工资元
18000
12000
8000
6000
4000
2500
2000
1500
1200
人数
总经理
副总经理
3
4
10
20
22
12
6
该公司月工资数据的众数为2000,中位数为2250,平均数为3115,极差为16800,公司的普通员工最关注的数据是
A.
中位数和众数
B.
平均数和众数
C.
平均数和中位数
D.
平均数和极差
在一次数学测试中,小明成绩120分,超过班级半数同学的成绩,分析得出这个结论所用的统计量是
A.
中位数
B.
众数
C.
平均数
D.
方差
在庆祝新中国成立70周年的校园歌唱比赛中,11名参赛同学的成绩各不相同,按照成绩取前5名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这11名同学成绩的
A.
平均数
B.
中位数
C.
众数
D.
方差
为了比较甲乙两足球队的身高谁更整齐,分别量出每人身高,发现两队的平均身高一样,甲、乙两队的方差分别是、,则下列说法正确的是
A.
甲、乙两队身高一样整齐
B.
甲队身高更整齐
C.
乙队身高更整齐
D.
无法确定甲、乙两队身高谁更整齐
已知数据1,2,3,3,4,5,则下列关于这组数据的说法,错误的是
A.
平均数是3
B.
中位数和众数都是3
C.
方差为10
D.
标准差是
为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高单位:的平均数与方差为:???则麦苗又高又整齐的是??
A.
甲
B.
乙
C.
丙
D.
丁
二、填空题
数据2,3,x,5,7的平均数是4,这组数据的众数是____________.
一组数据2,3,5,x,7,4,6,9的众数是4,则这组数据的中位数是____________.
在某次七年级期末测试中,甲乙两个班的数学平均成绩都是89分,且方差分别为,,则成绩比较稳定的是______班.
某公司要招聘职员,竟聘者需通过计算机、语言表达和写作能力测试,李丽的三项成绩百分制依次是70分,90分,80分,其中计算机成绩占,语言表达成绩占,写作能力成绩占,则李丽最终的成绩是______分.
甲、乙两人各进行10次射击比赛,平均成绩均为9环,方差分别是:,,则射击成绩较稳定的是______选填“甲”或“乙”.
某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数单位:分及方差,如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是______.
甲
乙
丙
丁
7
8
8
7
1
三、计算题
某商场统计了今年月A,B两种品牌冰箱的销售情况单位:台
A品牌:15,16,17,13,14
B品牌:10,14,15,20,16
分别求出A,B两种品牌冰箱数据的平均数和方差;
根据计算结果,比较该商场月这两种品牌冰箱月销售量的稳定性.
某校同学组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表分制:
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
甲队成绩的中位数是_______分,乙队成绩的众数是_____分;
计算乙队的平均成绩和方差;
已知甲队成绩的方差是分,则成绩较为整齐的是_____队.
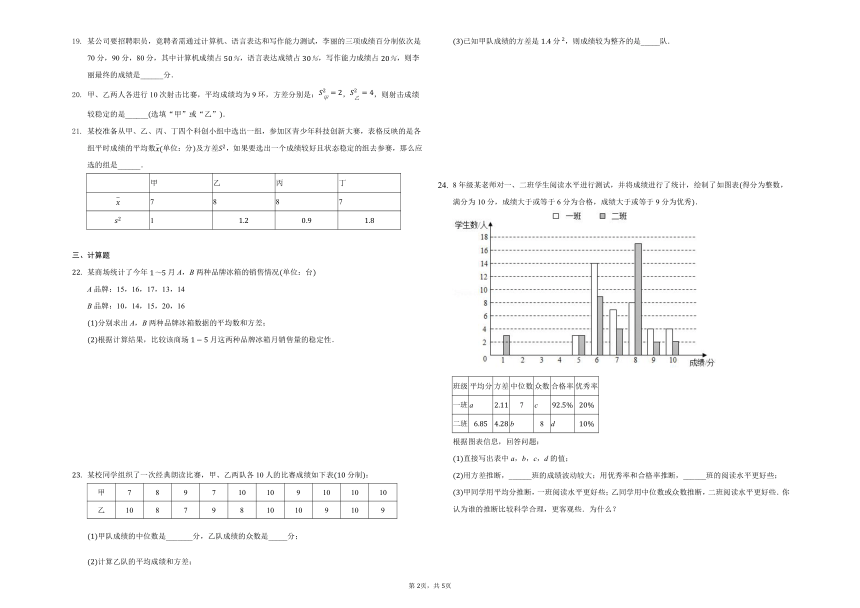
8年级某老师对一、二班学生阅读水平进行测试,并将成绩进行了统计,绘制了如图表得分为整数,满分为10分,成绩大于或等于6分为合格,成绩大于或等于9分为优秀.
班级
平均分
方差
中位数
众数
合格率
优秀率
一班
a
7
c
二班
b
8
d
根据图表信息,回答问题:
直接写出表中a,b,c,d的值;
用方差推断,______班的成绩波动较大;用优秀率和合格率推断,______班的阅读水平更好些;
甲同学用平均分推断,一班阅读水平更好些;乙同学用中位数或众数推断,二班阅读水平更好些.你认为谁的推断比较科学合理,更客观些.为什么?
某校初三体育考试选择项目中,选择篮球项目和排球项目的学生比较多.为了解学生掌握篮球技巧和排球技巧的水平情况,进行了抽样调查,过程如下,请补充完整.
收集数据??从选择篮球和排球的学生中各随机抽取16人,进行了体育测试,测试成绩十分制如下:
排球????10????????????10?????8??????9????????????9
?????????????
7?????10????4?????????10???
???????10
篮球??????9?
?????10?
?10???8
?????????
?6???10???
?????6
整理、描述数据???按如下分数段整理、描述这两组样本数据:
10
排球
1
1
2
7
5
篮球
说明:成绩分及以上为优秀,6分及以上为合格,6分以下为不合格.
分析数据???两组样本数据的平均数、中位数、众数如下表所示:
项目
平均数
中位数
众数
排球
10
篮球
得出结论
如果全校有160人选择篮球项目,达到优秀的人数约为______人;
初二年级的小明和小军看到上面数据后,小明说:排球项目整体水平较高.小军说:篮球项目整体水平较高.
你同意______?的看法,理由为______至少从两个不同的角度说明推断的合理性
答案
1.【答案】A
2.【答案】B
3.【答案】A
4.【答案】C
5.【答案】B
6.【答案】D
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】A
11.【答案】A
12.【答案】B
13.【答案】B
14.【答案】C
15.【答案】D
16.【答案】3
17.【答案】
18.【答案】甲
19.【答案】78
20.【答案】甲
21.【答案】丙
22.【答案】解:品牌冰箱数据的平均数为:台
B品牌冰箱数据的平均数为:台
,
,
该商场月A品牌冰箱月销售量更为稳定.
23.【答案】;10;
乙队的平均成绩是:,
则方差是:;
乙.
【解析】解:把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是分,
则中位数是分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:,10;
见答案;
甲队成绩的方差是,乙队成绩的方差是1,
成绩较为整齐的是乙队;
故答案为:乙.
24.【答案】(1),8,6,.
(2)二班?
一班
乙同学的推断比较科学合理,也更客观.
理由:虽然二班的平均分比一班低,但从条形图可以看出,二班有3名学生的成绩为1分,
在该组数据中属于极端值,平均分受极端值的影响较大;而中位数或众数不易受极端值得影响,
所以乙同学的推断更科学合理.
【解析】解:由图知:一班5分的3人,6分的14人,7分的7人,8分的8人,9分的4人,10分的4人;
二班1分的3人,5分的3人,6分的9人,7分的4人,8分的17人,9分的2人,10分的2人.
一班的平均分
;
二班共有学生40人,按分数从小到大排列后第20人是8分,第21人是8分,
所以.
一班14人得6分,故众数.
二班的合格率.
故a、b、c、d的值分别为:,8,6,.
因为,,,
故用方差推断二班的成绩波动较大;用优秀率和合格率推断,一班的成绩更好些;
故答案为:二、一.
乙同学的推断比较科学合理,也更客观.
理由:虽然二班的平均分比一班低,但从条形图可以看出,二班有3名学生的成绩为1分,
在该组数据中属于极端值,平均分受极端值的影响较大;而中位数或众数不易受极端值得影响,
所以乙同学的推断更科学合理.
25.【答案】?
小明?
;平均数接近,而排球成绩的中位数和众数都较高
【解析】
解:补全表格成绩:
人数
项目
10
排球
1
1
2
7
5
篮球
0
2
1
10
3
达到优秀的人数约为人;
故答案为:130;
同意小明的看法,理由为:平均数接近,而排球成绩的中位数和众数都较高.答案不唯一,理由需支持判断结论
故答案为:小明,平均数接近,而排球成绩的中位数和众数都较高.
第4页,共5页
第5页,共5页
复习检测
一、选择题
一组数据0、、3、2、1的极差是
A.
4
B.
3
C.
2
D.
1
下列命题为真命题的是
A.
若,则
B.
等角的余角相等
C.
同旁内角相等,两直线平行
D.
,,则A组数据更稳定
数据1,2,3,4,5,的平均数是
A.
2
B.
3
C.
4
D.
5
一组数据2,4,3,5,2的中位数是
A.
5
B.
C.
3
D.
甲、乙、丙、丁四位同学五次数学测验成绩统计如表所示,如果从这四位同学中,选出一位同学参加数学竞赛.那么应选谁去.
甲
乙
丙
丁
平均分
85
90
90
85
方差
50
42
50
42
A.
甲
B.
乙
C.
丙
D.
丁
甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均数都是环,方差分别是,,,,则射箭成绩最稳定的是
A.
甲
B.
乙
C.
丙
D.
丁
今年3月12日,某学校开展植树活动,某植树小组20名同学的年龄情况如下表:
?年龄岁
?12
?13
?14
?15
?16
?人数
?1
?4
?3
?5
?7
则这20名同学年龄的众数和中位数分别是
A.
15,14
B.
15,15
C.
16,14
D.
16,15
10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是
A.
B.
C.
D.
为评估一种农作物的种植效果,选了8块地作试验田,这8块地的亩产量单位:分别为,,,,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是
A.
,,,的平均数
B.
,,,的方差
C.
,,,的中位数
D.
,,,的众数
某公司全体职工的月工资如下:
月工资元
18000
12000
8000
6000
4000
2500
2000
1500
1200
人数
总经理
副总经理
3
4
10
20
22
12
6
该公司月工资数据的众数为2000,中位数为2250,平均数为3115,极差为16800,公司的普通员工最关注的数据是
A.
中位数和众数
B.
平均数和众数
C.
平均数和中位数
D.
平均数和极差
在一次数学测试中,小明成绩120分,超过班级半数同学的成绩,分析得出这个结论所用的统计量是
A.
中位数
B.
众数
C.
平均数
D.
方差
在庆祝新中国成立70周年的校园歌唱比赛中,11名参赛同学的成绩各不相同,按照成绩取前5名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这11名同学成绩的
A.
平均数
B.
中位数
C.
众数
D.
方差
为了比较甲乙两足球队的身高谁更整齐,分别量出每人身高,发现两队的平均身高一样,甲、乙两队的方差分别是、,则下列说法正确的是
A.
甲、乙两队身高一样整齐
B.
甲队身高更整齐
C.
乙队身高更整齐
D.
无法确定甲、乙两队身高谁更整齐
已知数据1,2,3,3,4,5,则下列关于这组数据的说法,错误的是
A.
平均数是3
B.
中位数和众数都是3
C.
方差为10
D.
标准差是
为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高单位:的平均数与方差为:???则麦苗又高又整齐的是??
A.
甲
B.
乙
C.
丙
D.
丁
二、填空题
数据2,3,x,5,7的平均数是4,这组数据的众数是____________.
一组数据2,3,5,x,7,4,6,9的众数是4,则这组数据的中位数是____________.
在某次七年级期末测试中,甲乙两个班的数学平均成绩都是89分,且方差分别为,,则成绩比较稳定的是______班.
某公司要招聘职员,竟聘者需通过计算机、语言表达和写作能力测试,李丽的三项成绩百分制依次是70分,90分,80分,其中计算机成绩占,语言表达成绩占,写作能力成绩占,则李丽最终的成绩是______分.
甲、乙两人各进行10次射击比赛,平均成绩均为9环,方差分别是:,,则射击成绩较稳定的是______选填“甲”或“乙”.
某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,表格反映的是各组平时成绩的平均数单位:分及方差,如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是______.
甲
乙
丙
丁
7
8
8
7
1
三、计算题
某商场统计了今年月A,B两种品牌冰箱的销售情况单位:台
A品牌:15,16,17,13,14
B品牌:10,14,15,20,16
分别求出A,B两种品牌冰箱数据的平均数和方差;
根据计算结果,比较该商场月这两种品牌冰箱月销售量的稳定性.
某校同学组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表分制:
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
甲队成绩的中位数是_______分,乙队成绩的众数是_____分;
计算乙队的平均成绩和方差;
已知甲队成绩的方差是分,则成绩较为整齐的是_____队.
8年级某老师对一、二班学生阅读水平进行测试,并将成绩进行了统计,绘制了如图表得分为整数,满分为10分,成绩大于或等于6分为合格,成绩大于或等于9分为优秀.
班级
平均分
方差
中位数
众数
合格率
优秀率
一班
a
7
c
二班
b
8
d
根据图表信息,回答问题:
直接写出表中a,b,c,d的值;
用方差推断,______班的成绩波动较大;用优秀率和合格率推断,______班的阅读水平更好些;
甲同学用平均分推断,一班阅读水平更好些;乙同学用中位数或众数推断,二班阅读水平更好些.你认为谁的推断比较科学合理,更客观些.为什么?
某校初三体育考试选择项目中,选择篮球项目和排球项目的学生比较多.为了解学生掌握篮球技巧和排球技巧的水平情况,进行了抽样调查,过程如下,请补充完整.
收集数据??从选择篮球和排球的学生中各随机抽取16人,进行了体育测试,测试成绩十分制如下:
排球????10????????????10?????8??????9????????????9
?????????????
7?????10????4?????????10???
???????10
篮球??????9?
?????10?
?10???8
?????????
?6???10???
?????6
整理、描述数据???按如下分数段整理、描述这两组样本数据:
10
排球
1
1
2
7
5
篮球
说明:成绩分及以上为优秀,6分及以上为合格,6分以下为不合格.
分析数据???两组样本数据的平均数、中位数、众数如下表所示:
项目
平均数
中位数
众数
排球
10
篮球
得出结论
如果全校有160人选择篮球项目,达到优秀的人数约为______人;
初二年级的小明和小军看到上面数据后,小明说:排球项目整体水平较高.小军说:篮球项目整体水平较高.
你同意______?的看法,理由为______至少从两个不同的角度说明推断的合理性
答案
1.【答案】A
2.【答案】B
3.【答案】A
4.【答案】C
5.【答案】B
6.【答案】D
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】A
11.【答案】A
12.【答案】B
13.【答案】B
14.【答案】C
15.【答案】D
16.【答案】3
17.【答案】
18.【答案】甲
19.【答案】78
20.【答案】甲
21.【答案】丙
22.【答案】解:品牌冰箱数据的平均数为:台
B品牌冰箱数据的平均数为:台
,
,
该商场月A品牌冰箱月销售量更为稳定.
23.【答案】;10;
乙队的平均成绩是:,
则方差是:;
乙.
【解析】解:把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是分,
则中位数是分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:,10;
见答案;
甲队成绩的方差是,乙队成绩的方差是1,
成绩较为整齐的是乙队;
故答案为:乙.
24.【答案】(1),8,6,.
(2)二班?
一班
乙同学的推断比较科学合理,也更客观.
理由:虽然二班的平均分比一班低,但从条形图可以看出,二班有3名学生的成绩为1分,
在该组数据中属于极端值,平均分受极端值的影响较大;而中位数或众数不易受极端值得影响,
所以乙同学的推断更科学合理.
【解析】解:由图知:一班5分的3人,6分的14人,7分的7人,8分的8人,9分的4人,10分的4人;
二班1分的3人,5分的3人,6分的9人,7分的4人,8分的17人,9分的2人,10分的2人.
一班的平均分
;
二班共有学生40人,按分数从小到大排列后第20人是8分,第21人是8分,
所以.
一班14人得6分,故众数.
二班的合格率.
故a、b、c、d的值分别为:,8,6,.
因为,,,
故用方差推断二班的成绩波动较大;用优秀率和合格率推断,一班的成绩更好些;
故答案为:二、一.
乙同学的推断比较科学合理,也更客观.
理由:虽然二班的平均分比一班低,但从条形图可以看出,二班有3名学生的成绩为1分,
在该组数据中属于极端值,平均分受极端值的影响较大;而中位数或众数不易受极端值得影响,
所以乙同学的推断更科学合理.
25.【答案】?
小明?
;平均数接近,而排球成绩的中位数和众数都较高
【解析】
解:补全表格成绩:
人数
项目
10
排球
1
1
2
7
5
篮球
0
2
1
10
3
达到优秀的人数约为人;
故答案为:130;
同意小明的看法,理由为:平均数接近,而排球成绩的中位数和众数都较高.答案不唯一,理由需支持判断结论
故答案为:小明,平均数接近,而排球成绩的中位数和众数都较高.
第4页,共5页
第5页,共5页
