2.4 用尺规作角 一课一练(含解析)
文档属性
| 名称 | 2.4 用尺规作角 一课一练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 18:09:23 | ||
图片预览



文档简介
初中数学北师大版七年级下学期 第二章 2.4 用尺规作角
一、单选题
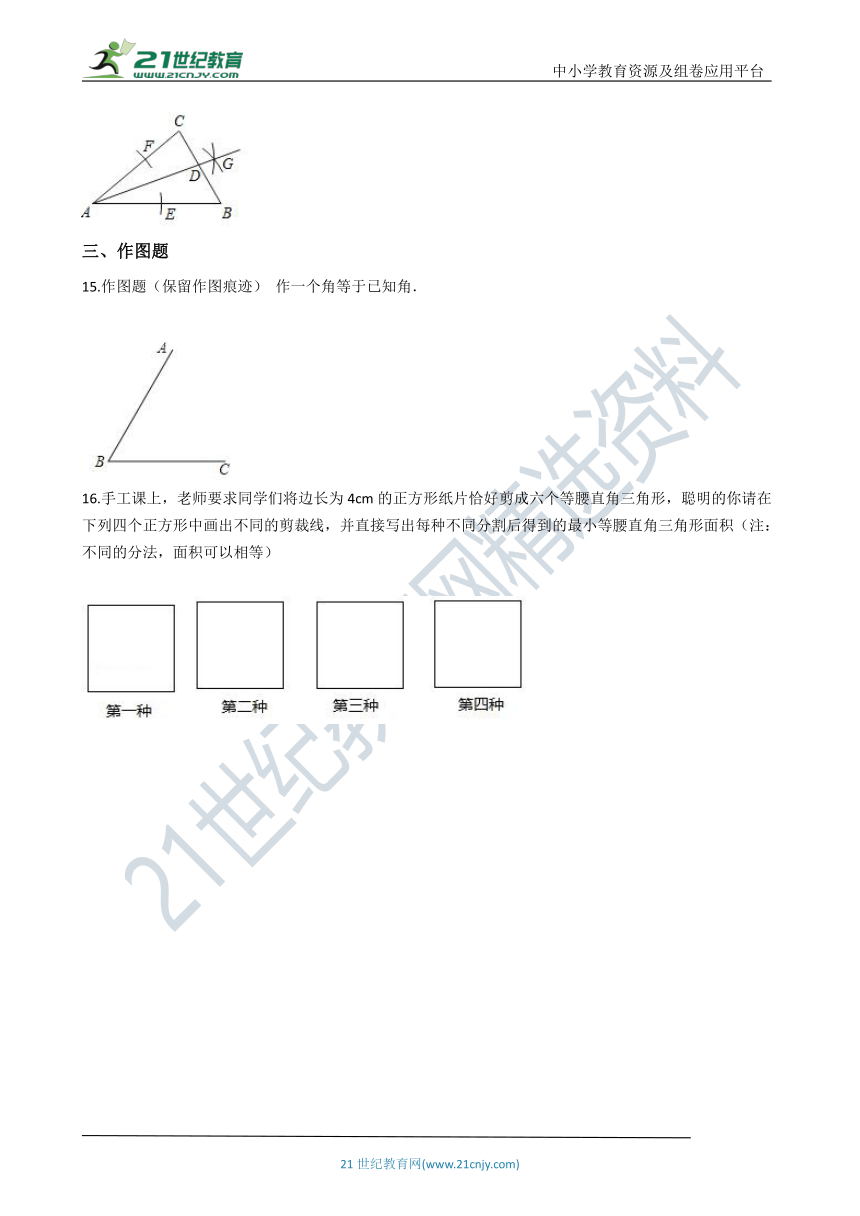
1.如图,用尺规作出∠OBF=∠AOB,所画痕迹是(??????? )
A.?以点B为圆心,OD为半径的弧????????????????????????????B.?以点C为圆心,DC为半径的弧
C.?以点E为圆心,OD为半径的弧????????????????????????????D.?以点E为圆心,DC为半径的弧
2.已知三边作三角形,用到的基本作图是( ? )
A.?作一个角等于已知角???????????????????????????????????????????B.?平分一个已知角
C.?在射线上截取一线段等于已知线段??????????????????????D.?作一条直线的垂线
3.如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG是( ??)
A.?以点C为圆心,OD为半径的弧????????????????????????????B.?以点C为圆心,DM为半径的弧
C.?以点E为圆心,OD为半径的弧????????????????????????????D.?以点E为圆心,DM为半径的弧
4.在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
A.?40°??????????????????????????????????????B.?50°????????????????????????????????????????C.?60°??????????????????????????????????????D.?70°
5.在△ABC中,AB=AC,∠A=80°,进行如下操作 ①以点B为圆心,以小于AB长为半径作弧,分别交BA、BC于点E,F;②分别以E,F为圆心,以大于 EF长为半径作弧,两弧交于点M;③作射线BM交AC于点D,则∠BDC的度数为(?? )
A.?100°?????????????????????????????????????B.?65°?????????????????????????????????????C.?75°?????????????????????????????????????D.?105°
6.已知点C在∠AOB的OB边上,用尺规过点C作CN∥OA,作图痕迹如图所示.下列对弧FG的描述,正确的是(??? )
A.?以点C为圆心,OD的长为半径的弧?????????????????????B.?以点C为圆心,OM的长为半径的弧
C.?以点E为圆心,DM的长为半径的弧?????????????????????D.?以点E为圆心,CE的长为半径的弧
7.如图,点 在 的边 上,用尺规作出了 ,作图痕迹中,弧 是(??? )
A.?以点 为圆心, 为半径的弧?????????????????????B.?以点 为圆心, 为半径的弧
C.?以点 为圆心, 为半径的弧?????????????????????D.?以点 为圆心, 为半径的弧
8.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是(?? )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
9.如图,在△ABC中,∠C=90°,∠B=32°,以A为圆心,任意长为半径画弧分别交AB , AC于点M和N , 再分别以M , N为圆心,大于 MN的长为半径画弧,两弧交于点P , 连接AP并延长交BC于点D , 则下列说法:
①AD是∠BAC的平分线;
②CD是△ADC的高;
③点D在AB的垂直平分线上;
④∠ADC=61°.
其中正确的有( )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题
10.下列语句是有关几何作图的叙述.
①以O为圆心作弧;②延长射线AB到点C;③作∠AOB,使∠AOB=∠1;④作直线AB,使AB=a;⑤过三角形ABC的顶点C作它的对边AB的平行线.其中正确的有________.(填序号即可)
11.在同一平面内.过直线上一点作已知直线的垂线,能作________条.
12.如图,AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F,为圆心,大于 长为半径作圆弧,两弧交于点G,作射线BG交CD于点H。若∠D=116°,则∠DHB的大小为________。
13.所谓尺规作图中的尺规是指:________.
14.如图,在△ABC中,∠ACB=80°,∠ABC=60°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于 EF的长为半径画弧,两弧相交于点G;③作射线AG交BC于点D . 则∠ADB的度数为________°
三、作图题
15.作图题(保留作图痕迹) 作一个角等于已知角.
16.手工课上,老师要求同学们将边长为4cm的正方形纸片恰好剪成六个等腰直角三角形,聪明的你请在下列四个正方形中画出不同的剪裁线,并直接写出每种不同分割后得到的最小等腰直角三角形面积(注:不同的分法,面积可以相等)
答案解析部分
一、单选题
1.【答案】 D
解:作∠OBF=∠AOB的作法,由图可知,
①以点O为圆心,以任意长为半径画圆,分别交射线OA、OB分别为点C,D;
②以点B为圆心,以OC为半径画圆,分别交射线BO、MB分别为点E,F;
③以点E为圆心,以CD为半径画圆,交于点N,连接BN即可得出∠OBF,则∠OBF=∠AOB.
故选D.
2.【答案】 C
解:根据三边做三角形用到的基本作图是:作一条线段等于已知线段.
故选C.
3.【答案】 D
解:根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧
故答案为::D
4.【答案】 A
解:∵根据作图过程和痕迹发现MN垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=35°,
∵CD=BC,
∴∠CDB=∠CBD=2∠A=70°,
∴∠C=40°,
故选A.
5.【答案】 D
解:∵AB=AC,∠A=80°,? ∴∠ABC=∠C=50°,?? 由题意可得:BD平分∠ABC,?? 则∠ABD=∠CBD=25°,?? ∴∠BDC的度数为:∠A+∠ABD=105°.?? 故答案为:D
6.【答案】 C
解:根据题意,所作出的是∠BCN=∠AOB,
根据作一个角等于已知角的作法,弧FG是以点E为圆心,DM为半径的弧.
故答案为:C.
7.【答案】 D
解:根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧.
故答案为:D.
8.【答案】 D
解:①根据作图的过程可知,AD是∠BAC的平分线.故①符合题意.
②如图,∵在△ABC中,∠C=90°,∠B=30°,∴∠CAB=60°.
又∵AD是∠BAC的平分线,∴∠1=∠2=∠CAB=30°,
∴∠3=90°﹣∠2=60°,即∠ADC=60°.故②符合题意.
③∵∠1=∠B=30°,∴AD=B
D.∴点D在AB的中垂线上.故③符合题意.
④∵如图,在直角△ACD中,∠2=30°,∴CD= AD.
∴BC=CD+BD= AD+AD= AD,S△DAC= AC?CD= AC?AD.
∴S△ABC= AC?BC= AC?A D= AC?AD.
∴S△DAC:S△ABC 。故④符合题意.
综上所述,正确的结论是:①②③④,,共有4个。
故答案为:D.
9.【答案】 C
解:根据作法可得AD是∠BAC的平分线,故①正确;
∵∠C=90°,
∴CD是△ADC的高,故②正确;
∵∠C=90°,∠B=32°,
∴∠CAB=58°,
∵AD是∠BAC的平分线,
∴∠CAD=∠DAB=29°,
∴AD≠BD ,
∴点D不在AB的垂直平分线上,故③错误;
∵∠CAD=29°,∠C=90°,
∴∠CDA=61°,故④正确;
共有3个正确,
选C.
二、填空题
10.【答案】 ③⑤
解:①以O为圆心作弧可以画出无数条弧,因为半径不固定,所以叙述错误;
②射线AB是由A向B向无限延伸,所以叙述错误;
③根据作一个角等于已知角的作法,可以作一个角∠AOB,使∠AOB等于已知∠1,所以叙述正确;
④直线可以向两方无限延伸,所以叙述错误;
⑤根据平行公理:过直线外一点有且只有一条直线与已知直线平行,可以过三角形ABC的顶点C作它的对边AB的平行线,所以叙述正确.
所以正确的有③⑤.
故答案为:③⑤.
11.【答案】 1
过已知直线上的一点有且只有一条直线垂直于已知直线
12.【答案】 32°
解:∵AB∥CD,
∴∠D+∠ABD=180°,∠DHB=∠ABH
又∵∠D=116°,
∴∠ABD=64°,
由作法知,BH是∠ABD的平分线,
∴∠DHB= ∠ABD=32°
13.【答案】 没有刻度的直尺和圆规
解:由尺规作图的概念可知:尺规作图中的尺规指的是没有刻度的直尺和圆规.
14.【答案】 100
解:根据已知条件中的作图步骤知,AG是∠CAB的平分线,
∵∠ACB=80°,∠ABC=60°,
∴∠CAB=40°,
∴∠BAD=20°;
在△ADC中,∠B=60°,∠CAD=20°,
∴∠ADB=100°
三、作图题
15.【答案】 解: 如图所示:∠DEF即为所求
16.【答案】 解:根据分析,可得
.
(1)第一种情况下,分割后得到的最小等腰直角三角形是△AEH、△BEF、△CFG、△DHG,
每个最小的等腰直角三角形的面积是:
(4÷2)×(4÷2)÷2
=2×2÷2
=2(cm2)
(2)第二种情况下,分割后得到的最小等腰直角三角形是△AEO、△BEO、△BFO、△CFO,
每个最小的等腰直角三角形的面积是:
(4÷2)×(4÷2)÷2
=2×2÷2
=2(cm2)
(3)第三种情况下,分割后得到的最小等腰直角三角形是△AHO、△DHO、△BFO、△CFO,
每个最小的等腰直角三角形的面积是:
(4÷2)×(4÷2)÷2
=2×2÷2
=2(cm2)
(4)第四种情况下,分割后得到的最小等腰直角三角形是△AEI、△OEI,
每个最小的等腰直角三角形的面积是:
(4÷2)×(4÷2)÷2÷2
=2×2÷2÷2
=1(cm2).
一、单选题
1.如图,用尺规作出∠OBF=∠AOB,所画痕迹是(??????? )
A.?以点B为圆心,OD为半径的弧????????????????????????????B.?以点C为圆心,DC为半径的弧
C.?以点E为圆心,OD为半径的弧????????????????????????????D.?以点E为圆心,DC为半径的弧
2.已知三边作三角形,用到的基本作图是( ? )
A.?作一个角等于已知角???????????????????????????????????????????B.?平分一个已知角
C.?在射线上截取一线段等于已知线段??????????????????????D.?作一条直线的垂线
3.如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC,作图痕迹中,弧FG是( ??)
A.?以点C为圆心,OD为半径的弧????????????????????????????B.?以点C为圆心,DM为半径的弧
C.?以点E为圆心,OD为半径的弧????????????????????????????D.?以点E为圆心,DM为半径的弧
4.在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
A.?40°??????????????????????????????????????B.?50°????????????????????????????????????????C.?60°??????????????????????????????????????D.?70°
5.在△ABC中,AB=AC,∠A=80°,进行如下操作 ①以点B为圆心,以小于AB长为半径作弧,分别交BA、BC于点E,F;②分别以E,F为圆心,以大于 EF长为半径作弧,两弧交于点M;③作射线BM交AC于点D,则∠BDC的度数为(?? )
A.?100°?????????????????????????????????????B.?65°?????????????????????????????????????C.?75°?????????????????????????????????????D.?105°
6.已知点C在∠AOB的OB边上,用尺规过点C作CN∥OA,作图痕迹如图所示.下列对弧FG的描述,正确的是(??? )
A.?以点C为圆心,OD的长为半径的弧?????????????????????B.?以点C为圆心,OM的长为半径的弧
C.?以点E为圆心,DM的长为半径的弧?????????????????????D.?以点E为圆心,CE的长为半径的弧
7.如图,点 在 的边 上,用尺规作出了 ,作图痕迹中,弧 是(??? )
A.?以点 为圆心, 为半径的弧?????????????????????B.?以点 为圆心, 为半径的弧
C.?以点 为圆心, 为半径的弧?????????????????????D.?以点 为圆心, 为半径的弧
8.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是(?? )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
9.如图,在△ABC中,∠C=90°,∠B=32°,以A为圆心,任意长为半径画弧分别交AB , AC于点M和N , 再分别以M , N为圆心,大于 MN的长为半径画弧,两弧交于点P , 连接AP并延长交BC于点D , 则下列说法:
①AD是∠BAC的平分线;
②CD是△ADC的高;
③点D在AB的垂直平分线上;
④∠ADC=61°.
其中正确的有( )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题
10.下列语句是有关几何作图的叙述.
①以O为圆心作弧;②延长射线AB到点C;③作∠AOB,使∠AOB=∠1;④作直线AB,使AB=a;⑤过三角形ABC的顶点C作它的对边AB的平行线.其中正确的有________.(填序号即可)
11.在同一平面内.过直线上一点作已知直线的垂线,能作________条.
12.如图,AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F,为圆心,大于 长为半径作圆弧,两弧交于点G,作射线BG交CD于点H。若∠D=116°,则∠DHB的大小为________。
13.所谓尺规作图中的尺规是指:________.
14.如图,在△ABC中,∠ACB=80°,∠ABC=60°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于 EF的长为半径画弧,两弧相交于点G;③作射线AG交BC于点D . 则∠ADB的度数为________°
三、作图题
15.作图题(保留作图痕迹) 作一个角等于已知角.
16.手工课上,老师要求同学们将边长为4cm的正方形纸片恰好剪成六个等腰直角三角形,聪明的你请在下列四个正方形中画出不同的剪裁线,并直接写出每种不同分割后得到的最小等腰直角三角形面积(注:不同的分法,面积可以相等)
答案解析部分
一、单选题
1.【答案】 D
解:作∠OBF=∠AOB的作法,由图可知,
①以点O为圆心,以任意长为半径画圆,分别交射线OA、OB分别为点C,D;
②以点B为圆心,以OC为半径画圆,分别交射线BO、MB分别为点E,F;
③以点E为圆心,以CD为半径画圆,交于点N,连接BN即可得出∠OBF,则∠OBF=∠AOB.
故选D.
2.【答案】 C
解:根据三边做三角形用到的基本作图是:作一条线段等于已知线段.
故选C.
3.【答案】 D
解:根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧
故答案为::D
4.【答案】 A
解:∵根据作图过程和痕迹发现MN垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=35°,
∵CD=BC,
∴∠CDB=∠CBD=2∠A=70°,
∴∠C=40°,
故选A.
5.【答案】 D
解:∵AB=AC,∠A=80°,? ∴∠ABC=∠C=50°,?? 由题意可得:BD平分∠ABC,?? 则∠ABD=∠CBD=25°,?? ∴∠BDC的度数为:∠A+∠ABD=105°.?? 故答案为:D
6.【答案】 C
解:根据题意,所作出的是∠BCN=∠AOB,
根据作一个角等于已知角的作法,弧FG是以点E为圆心,DM为半径的弧.
故答案为:C.
7.【答案】 D
解:根据作一个角等于已知角可得弧FG是以点E为圆心,DM为半径的弧.
故答案为:D.
8.【答案】 D
解:①根据作图的过程可知,AD是∠BAC的平分线.故①符合题意.
②如图,∵在△ABC中,∠C=90°,∠B=30°,∴∠CAB=60°.
又∵AD是∠BAC的平分线,∴∠1=∠2=∠CAB=30°,
∴∠3=90°﹣∠2=60°,即∠ADC=60°.故②符合题意.
③∵∠1=∠B=30°,∴AD=B
D.∴点D在AB的中垂线上.故③符合题意.
④∵如图,在直角△ACD中,∠2=30°,∴CD= AD.
∴BC=CD+BD= AD+AD= AD,S△DAC= AC?CD= AC?AD.
∴S△ABC= AC?BC= AC?A D= AC?AD.
∴S△DAC:S△ABC 。故④符合题意.
综上所述,正确的结论是:①②③④,,共有4个。
故答案为:D.
9.【答案】 C
解:根据作法可得AD是∠BAC的平分线,故①正确;
∵∠C=90°,
∴CD是△ADC的高,故②正确;
∵∠C=90°,∠B=32°,
∴∠CAB=58°,
∵AD是∠BAC的平分线,
∴∠CAD=∠DAB=29°,
∴AD≠BD ,
∴点D不在AB的垂直平分线上,故③错误;
∵∠CAD=29°,∠C=90°,
∴∠CDA=61°,故④正确;
共有3个正确,
选C.
二、填空题
10.【答案】 ③⑤
解:①以O为圆心作弧可以画出无数条弧,因为半径不固定,所以叙述错误;
②射线AB是由A向B向无限延伸,所以叙述错误;
③根据作一个角等于已知角的作法,可以作一个角∠AOB,使∠AOB等于已知∠1,所以叙述正确;
④直线可以向两方无限延伸,所以叙述错误;
⑤根据平行公理:过直线外一点有且只有一条直线与已知直线平行,可以过三角形ABC的顶点C作它的对边AB的平行线,所以叙述正确.
所以正确的有③⑤.
故答案为:③⑤.
11.【答案】 1
过已知直线上的一点有且只有一条直线垂直于已知直线
12.【答案】 32°
解:∵AB∥CD,
∴∠D+∠ABD=180°,∠DHB=∠ABH
又∵∠D=116°,
∴∠ABD=64°,
由作法知,BH是∠ABD的平分线,
∴∠DHB= ∠ABD=32°
13.【答案】 没有刻度的直尺和圆规
解:由尺规作图的概念可知:尺规作图中的尺规指的是没有刻度的直尺和圆规.
14.【答案】 100
解:根据已知条件中的作图步骤知,AG是∠CAB的平分线,
∵∠ACB=80°,∠ABC=60°,
∴∠CAB=40°,
∴∠BAD=20°;
在△ADC中,∠B=60°,∠CAD=20°,
∴∠ADB=100°
三、作图题
15.【答案】 解: 如图所示:∠DEF即为所求
16.【答案】 解:根据分析,可得
.
(1)第一种情况下,分割后得到的最小等腰直角三角形是△AEH、△BEF、△CFG、△DHG,
每个最小的等腰直角三角形的面积是:
(4÷2)×(4÷2)÷2
=2×2÷2
=2(cm2)
(2)第二种情况下,分割后得到的最小等腰直角三角形是△AEO、△BEO、△BFO、△CFO,
每个最小的等腰直角三角形的面积是:
(4÷2)×(4÷2)÷2
=2×2÷2
=2(cm2)
(3)第三种情况下,分割后得到的最小等腰直角三角形是△AHO、△DHO、△BFO、△CFO,
每个最小的等腰直角三角形的面积是:
(4÷2)×(4÷2)÷2
=2×2÷2
=2(cm2)
(4)第四种情况下,分割后得到的最小等腰直角三角形是△AEI、△OEI,
每个最小的等腰直角三角形的面积是:
(4÷2)×(4÷2)÷2÷2
=2×2÷2÷2
=1(cm2).
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
