人教版数学九年级下册 第28章 28.2解直角三角形及其应用同步测试试题(word解析版)
文档属性
| 名称 | 人教版数学九年级下册 第28章 28.2解直角三角形及其应用同步测试试题(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 467.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 00:00:00 | ||
图片预览


文档简介
解直角三角形及其应用同步测试试题(一)
一.选择题
1.如图,在△ABC中,∠BAC=120°,AC=6,AB=4,则BC的长是( )
A.6
B.2
C.2
D.9
2.如图,在△ABC中,∠ACB=90°,D是AB的中点,若CD=5,AC=8,则tanA=( )
A.
B.
C.
D.
3.如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为( )
A.10tan36°
B.10cos36°
C.10sin36°
D.
4.在Rt△ABC中,∠C=90°,cosA=,∠B的平分线BD交AC于点D,若AD=16,则BC长为( )
A.6
B.8
C.8
D.12
5.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距200m,则图书馆A到公路的距离AB为( )
A.100m
B.100m
C.100m
D.
m
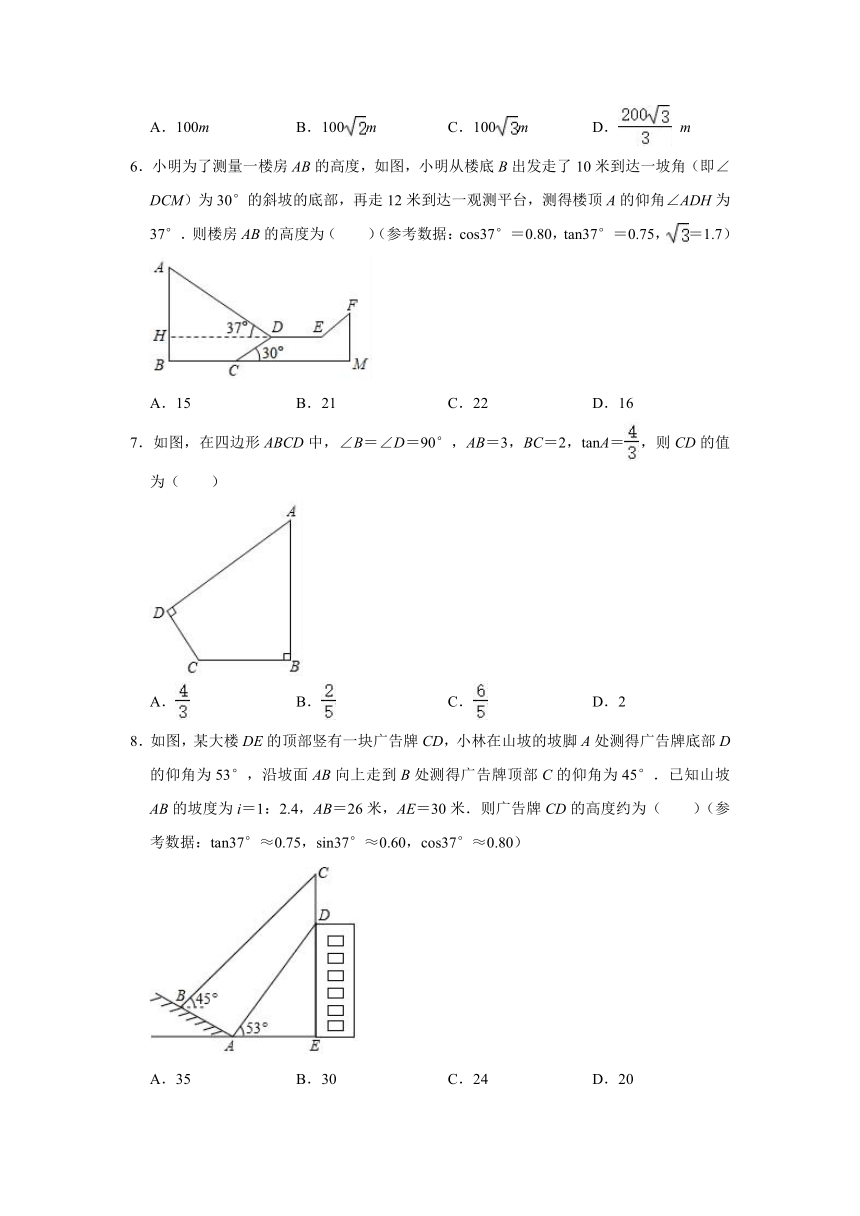
6.小明为了测量一楼房AB的高度,如图,小明从楼底B出发走了10米到达一坡角(即∠DCM)为30°的斜坡的底部,再走12米到达一观测平台,测得楼顶A的仰角∠ADH为37°.则楼房AB的高度为( )(参考数据:cos37°=0.80,tan37°=0.75,=1.7)
A.15
B.21
C.22
D.16
7.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为( )
A.
B.
C.
D.2
8.如图,某大楼DE的顶部竖有一块广告牌CD,小林在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°.已知山坡AB的坡度为i=1:2.4,AB=26米,AE=30米.则广告牌CD的高度约为( )(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
A.35
B.30
C.24
D.20
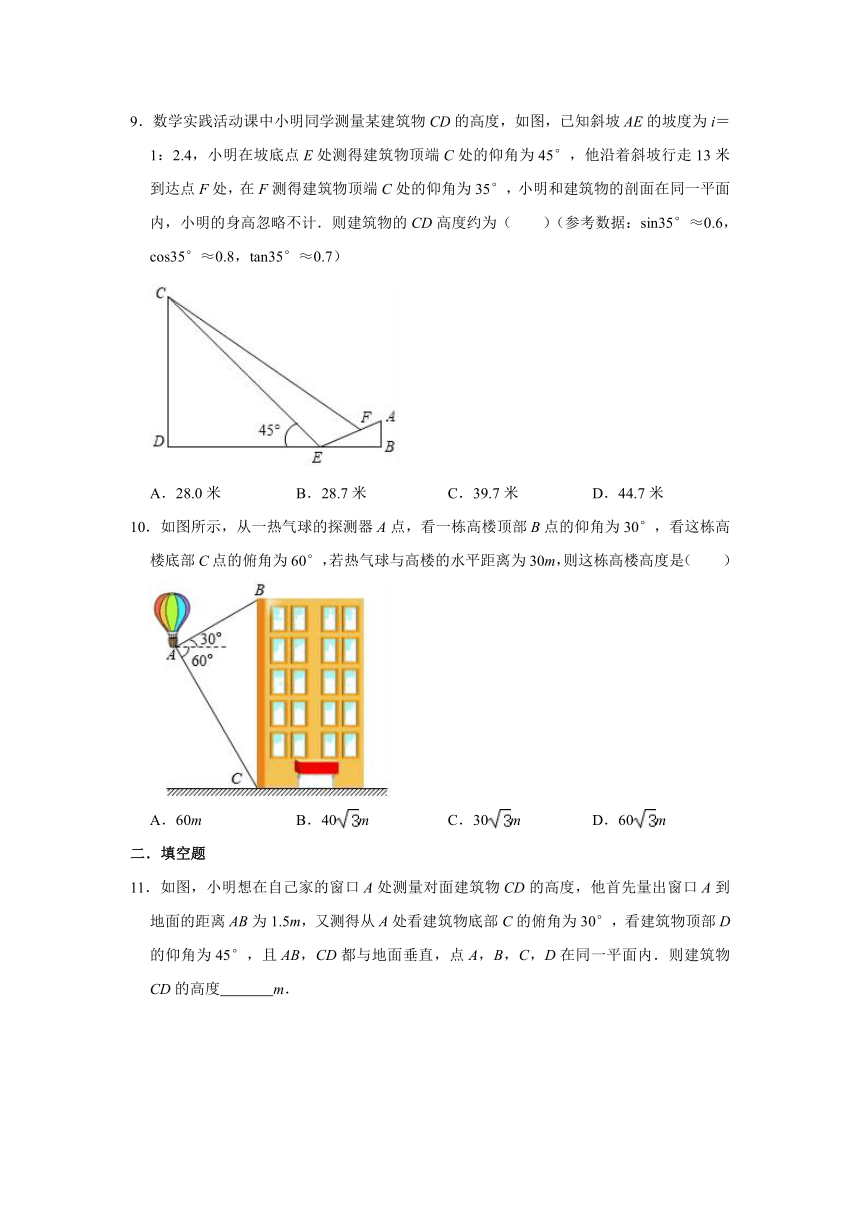
9.数学实践活动课中小明同学测量某建筑物CD的高度,如图,已知斜坡AE的坡度为i=1:2.4,小明在坡底点E处测得建筑物顶端C处的仰角为45°,他沿着斜坡行走13米到达点F处,在F测得建筑物顶端C处的仰角为35°,小明和建筑物的剖面在同一平面内,小明的身高忽略不计.则建筑物的CD高度约为( )(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)
A.28.0米
B.28.7米
C.39.7米
D.44.7米
10.如图所示,从一热气球的探测器A点,看一栋高楼顶部B点的仰角为30°,看这栋高楼底部C点的俯角为60°,若热气球与高楼的水平距离为30m,则这栋高楼高度是( )
A.60m
B.40m
C.30m
D.60m
二.填空题
11.如图,小明想在自己家的窗口A处测量对面建筑物CD的高度,他首先量出窗口A到地面的距离AB为1.5m,又测得从A处看建筑物底部C的俯角为30°,看建筑物顶部D的仰角为45°,且AB,CD都与地面垂直,点A,B,C,D在同一平面内.则建筑物CD的高度
m.
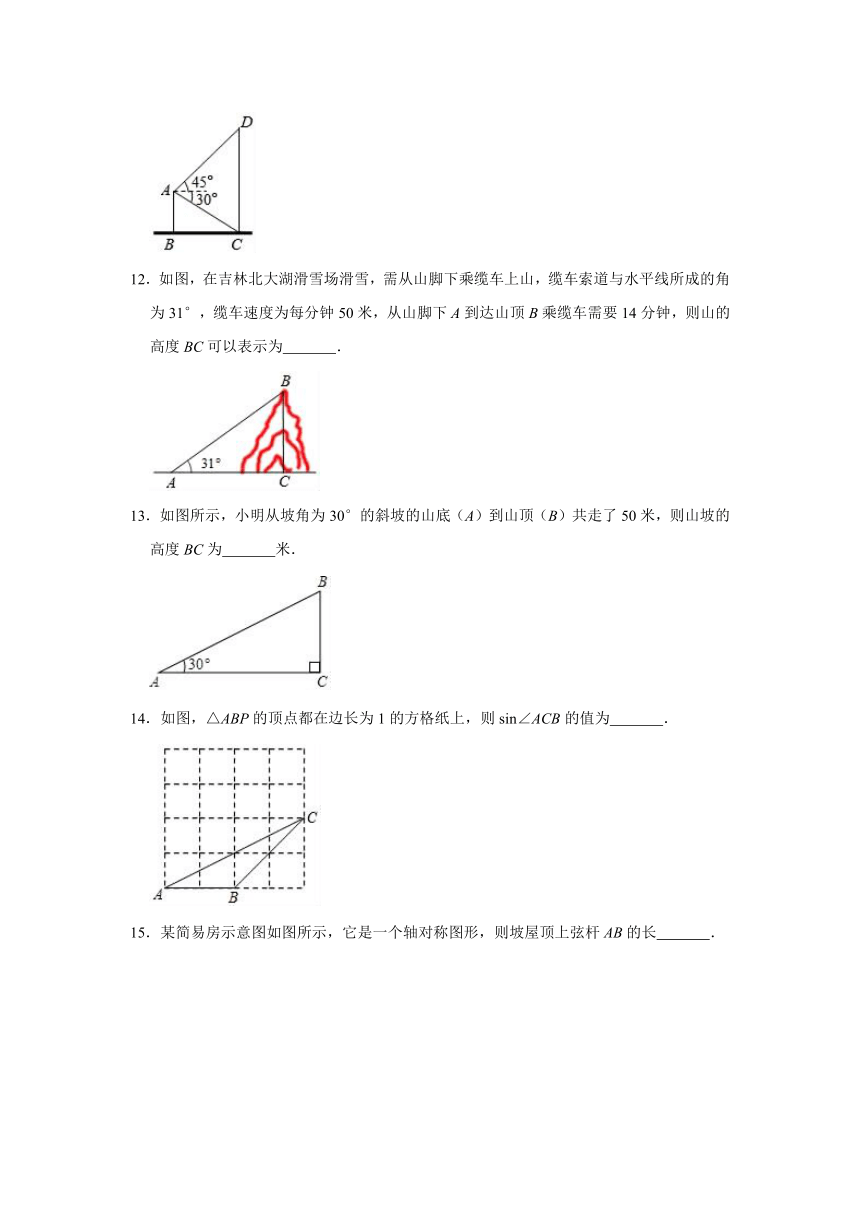
12.如图,在吉林北大湖滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为31°,缆车速度为每分钟50米,从山脚下A到达山顶B乘缆车需要14分钟,则山的高度BC可以表示为
.
13.如图所示,小明从坡角为30°的斜坡的山底(A)到山顶(B)共走了50米,则山坡的高度BC为
米.
14.如图,△ABP的顶点都在边长为1的方格纸上,则sin∠ACB的值为
.
15.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长
.
三.解答题
16.某游乐场一转角滑梯如图所示,滑梯立柱AB、CD均垂直于地面,点E在线段BD上,在C点测得A的仰角为30°、点E的俯角也为30°,测得B、E间距离为9米,立柱AB高30米.
(1)∠CED的度数是
(直接写出);
(2)求立柱CD的高.(结果保留根号)
17.如图,飞机A在地面目标B的正上方1000米处,飞行员测得另一地面目标C的俯角为30°,求B,C之间的距离(精确到0.1米).
(参考数据:sin30°=,cos30°=,tan30°=,=1.7321,sin60°=,cos60°=,tan60°=)
18.“建设美丽的新农村”正在如火如荼建设当中,其中某村的标志性雕塑如图,某中学九年级数学兴趣小组想测量雕塑AB的高度,小敏在雕塑前C、D两点处用测角仪测得顶端A的仰角分别为45°和30°,测角仪高EC=FD=1m,EF=4m,求该雕塑的高度.(结果保留根号)
19.某数学兴趣小组要测量实验大楼部分楼体的高度(如图1所示,CD部分),在起点A处测得大楼部分楼体CD的顶端C点的仰角为45°,底端D点的仰角为30°,在同一剖面沿水平地面向前走16米到达B处,测得顶端C的仰角为63.4°(如图2所示),求大楼部分楼体CD的高度约为多少米?(精确到1米)(参考数据:sin63.4°≈0.89,cos63.4°≈0.45,tan63.4°≈2.00,≈1.41,≈1.73)
参考答案与试题解析
一.选择题
1.【解答】解:过点C作CD⊥AB,交BA的延长线于点D,
∵∠BAC=120°,
∴∠DAC=180°﹣120°=60°,
∴∠ACD=30°,
∴AD=AC=3,
∴BD=AB+AD=7,
由勾股定理得,CD==3,
在Rt△BCD中,BC==2,
故选:B.
2.【解答】解:∵∠ACB=90°,D是AB的中点,CD=5,
∴AB=2CD=10,
∵AC=8,AB=10,
∴BC==6,
∴tanA===.
故选:C.
3.【解答】解:在Rt△ABC中,sinB=,
∴AC=ABsinB=10sin36°,
故选:C.
4.【解答】解:如图,
∵cosA=,
∴∠A=30°,
∵∠C=90°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠ABD=∠A=∠CBD=30°,
∴DB=DA=16,
∴BC=BDcos30°=16×=8,
故选:C.
5.【解答】解:由题意得,∠AOB=90°﹣60°=30°,
∴AB=OA=100(m),
故选:A.
6.【解答】解:作DN⊥BM于N,如图:
则HB=DN,DH=BN,
∵∠DCN=30°,CD=12米,
∴HB=DN=CD=6米,
CN=DN=6米,
∴DH=BN=BC+CN=10+6(米),
在Rt△ADH中,tan∠ADH==tan37°=0.75,
∴AH=0.75DH=0.75×(10+6)=15.15米,
∴AB=AH+HB=15.15+6≈21(米),
即楼房AB的高度约为21米.
故选:B.
7.【解答】解:延长AD、BC,两线交于O,
∵在Rt△ABO中,∠B=90°,tanA==,AB=3,
∴OB=4,
∵BC=2,
∴OC=OB﹣BC=4﹣2=2,
在Rt△ABO中,∠B=90°,AB=3,OB=4,由勾股定理得:AO=5,
∵∠ADC=90°,
∴∠ODC=90°=∠B,
∵∠O=∠O,
∴△ODC∽△OBA,
∴=,
∴=,
解得:DC=,
故选:C.
8.【解答】解:过B作BG⊥DE于G,BH⊥AE于H,如图:
则BG=AH+AE,GE=BH,
在Rt△ABF中,i=tan∠BAH=1:2.4=,
∴AH=2.4BH,
∴AB==2.6BH=26,
∴BH=10,AH=24,
∴BG=AH+AE=24+30=54,
在Rt△BGC中,∠CBG=45°,
∴CG=BG=54.
在Rt△ADE中,∠DAE=53°,
∴∠ADE=90°=53°=37°,
∵tan∠ADE==tan37°≈0.75,
∴DE=AE=40.
∴CD=CG+GE﹣DE=54+10﹣40=24(米);
即广告牌CD的高度约为24米;
故选:C.
9.【解答】解:过点F作FG⊥BD于G,FH⊥CD于H,如图所示:
则∠CFH=35°,四边形DGFH是矩形,
∴HF=DG,DH=FG,
∵斜坡AE的坡度为i=1:2.4,
∴设FG=x米,则EG=2.4x米,
在Rt△FGE中,由勾股定理得:EF2=FG2+EG2,
即:132=x2+(2.4x)2,
解得:x=5,
∴FG=5,EG=12,
∵∠CED=45°,
∴△CDE是等腰直角三角形,
∴CD=DE,
设CD=y米,则CH=(y﹣5)米,HF=(y+12)米,
Rt△CHF中,tan∠CFH=,
即tan35°=,则y﹣5=tan35°×(y+12),即y﹣5=0.7×(y+12),
解得:y≈44.7,
即建筑物的CD高度约为44.7米;
故选:D.
10.【解答】解:过A作AD⊥BC,垂足为D
在Rt△ABD中,∵∠BAD=30°,AD=30m,
∴BD=ADtan30°=30×=10(m),
在Rt△ACD中,∵∠CAD=60°,AD=30m,
∴CD=ADtan60°=30×=30(m),
∴BC=BD+CD=10+30=40(m),
即这栋高楼高度是40m.
故选:B.
二.填空题(共5小题)
11.【解答】解:如图,作AE⊥CD于E,则四边形ABCE为矩形,
∴CE=AB=1.5m,AE=BC,
在Rt△ACE中,tan∠CAE=,
∴AE===(m),
在Rt△ADE中,∵∠DAE=45°,
∴△ADE为等腰直角三角形,
∴DE=AE=m,
又∵CE=AB=1.5m,
∴CD=CE+DE=1.5+=(m),
答:建筑物CD的高度为m.
故答案为:.
12.【解答】解:由题意得,AB=50×14=700(米),
在Rt△ABC中,∠BAC=31°,sin∠BAC=,
∴BC=ABsin∠BAC=700sin31°(米),
故答案为:700sin31°米.
13.【解答】解:在Rt△ABC中,∠ACB=90°,∠A=30°,
∴BC=AB=×50=25(米),
故答案为:25.
14.【解答】解:过点B作BD⊥AC,垂足为D.
由题图知:AB=2,BC==2,
AC==2.
∵S△ABC=AB×CE=AC×BD,
∴×2×2=×2×BD,
∴BD=.
在Rt△BCD中,
sin∠ACB==
=.
故答案为:.
15.【解答】解:过A点作AD⊥BC于点D,
∵BC=3+0.3×2=3.6(m),AB=AC,
∴BD==1.8m,
∴=(m).
故答案为:.
三.解答题(共4小题)
16.【解答】解:(1)作CH⊥AB于H,如图所示:
由题意得:∠HCE=30°,CH∥BD,
∴∠CED=∠HCE=30°;
故答案为:30°;
(2)∵CH⊥AB,CD⊥BD,AB⊥BD,
∴四边形HBDC为矩形,
∴BD=CH,BH=CD,
由题意得,∠ACH=30°,∠CED=30°,
设CD=x
米,则AH=(30﹣x)米,
在Rt△AHC中,HC==(30﹣x),
则BD=CH=(30﹣x),
∴ED=(30﹣x)﹣9,
在Rt△CDE中,∠CED=30°,
∴ED=CD=x,
∴(30﹣x)﹣9=x,
解得,x=15﹣,
即立柱CD的高为(15﹣)米.
17.【解答】解:如图所示:
∵AD∥BC,
∴∠C=∠DAC=30°,
∵AB⊥BC,
∴∠ABC=90°,
∴BC=AB=1000≈1732.1(米),
即B,C之间的距离约为1732.1米.
18.【解答】解:如图,由题意可知PB=EC=1,
在Rt△APF与Rt△APE中,∠AFP=30°,∠AEP=45°,
设AP=x,则PE=x,,,
解得,
∴.
即该雕塑的高度为.
19.【解答】解:设楼高CE为x米,
∵在Rt△AEC中,∠CAE=45°,
∴AE=CE=x,
∵AB=16,
∴BE=x﹣16,
在Rt△CEB中,CE=BEtan63.4°≈2(x﹣16),
∴2(x﹣16)=x,
解得:x=32(米),
在Rt△DAE中,DE=AEtan30°=32×=,
∴CD=CE﹣DE=32﹣≈14(米),
答:大楼部分楼体CD的高度约为14米.
一.选择题
1.如图,在△ABC中,∠BAC=120°,AC=6,AB=4,则BC的长是( )
A.6
B.2
C.2
D.9
2.如图,在△ABC中,∠ACB=90°,D是AB的中点,若CD=5,AC=8,则tanA=( )
A.
B.
C.
D.
3.如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为( )
A.10tan36°
B.10cos36°
C.10sin36°
D.
4.在Rt△ABC中,∠C=90°,cosA=,∠B的平分线BD交AC于点D,若AD=16,则BC长为( )
A.6
B.8
C.8
D.12
5.如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东60°方向,且与他相距200m,则图书馆A到公路的距离AB为( )
A.100m
B.100m
C.100m
D.
m
6.小明为了测量一楼房AB的高度,如图,小明从楼底B出发走了10米到达一坡角(即∠DCM)为30°的斜坡的底部,再走12米到达一观测平台,测得楼顶A的仰角∠ADH为37°.则楼房AB的高度为( )(参考数据:cos37°=0.80,tan37°=0.75,=1.7)
A.15
B.21
C.22
D.16
7.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为( )
A.
B.
C.
D.2
8.如图,某大楼DE的顶部竖有一块广告牌CD,小林在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°.已知山坡AB的坡度为i=1:2.4,AB=26米,AE=30米.则广告牌CD的高度约为( )(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
A.35
B.30
C.24
D.20
9.数学实践活动课中小明同学测量某建筑物CD的高度,如图,已知斜坡AE的坡度为i=1:2.4,小明在坡底点E处测得建筑物顶端C处的仰角为45°,他沿着斜坡行走13米到达点F处,在F测得建筑物顶端C处的仰角为35°,小明和建筑物的剖面在同一平面内,小明的身高忽略不计.则建筑物的CD高度约为( )(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)
A.28.0米
B.28.7米
C.39.7米
D.44.7米
10.如图所示,从一热气球的探测器A点,看一栋高楼顶部B点的仰角为30°,看这栋高楼底部C点的俯角为60°,若热气球与高楼的水平距离为30m,则这栋高楼高度是( )
A.60m
B.40m
C.30m
D.60m
二.填空题
11.如图,小明想在自己家的窗口A处测量对面建筑物CD的高度,他首先量出窗口A到地面的距离AB为1.5m,又测得从A处看建筑物底部C的俯角为30°,看建筑物顶部D的仰角为45°,且AB,CD都与地面垂直,点A,B,C,D在同一平面内.则建筑物CD的高度
m.
12.如图,在吉林北大湖滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为31°,缆车速度为每分钟50米,从山脚下A到达山顶B乘缆车需要14分钟,则山的高度BC可以表示为
.
13.如图所示,小明从坡角为30°的斜坡的山底(A)到山顶(B)共走了50米,则山坡的高度BC为
米.
14.如图,△ABP的顶点都在边长为1的方格纸上,则sin∠ACB的值为
.
15.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长
.
三.解答题
16.某游乐场一转角滑梯如图所示,滑梯立柱AB、CD均垂直于地面,点E在线段BD上,在C点测得A的仰角为30°、点E的俯角也为30°,测得B、E间距离为9米,立柱AB高30米.
(1)∠CED的度数是
(直接写出);
(2)求立柱CD的高.(结果保留根号)
17.如图,飞机A在地面目标B的正上方1000米处,飞行员测得另一地面目标C的俯角为30°,求B,C之间的距离(精确到0.1米).
(参考数据:sin30°=,cos30°=,tan30°=,=1.7321,sin60°=,cos60°=,tan60°=)
18.“建设美丽的新农村”正在如火如荼建设当中,其中某村的标志性雕塑如图,某中学九年级数学兴趣小组想测量雕塑AB的高度,小敏在雕塑前C、D两点处用测角仪测得顶端A的仰角分别为45°和30°,测角仪高EC=FD=1m,EF=4m,求该雕塑的高度.(结果保留根号)
19.某数学兴趣小组要测量实验大楼部分楼体的高度(如图1所示,CD部分),在起点A处测得大楼部分楼体CD的顶端C点的仰角为45°,底端D点的仰角为30°,在同一剖面沿水平地面向前走16米到达B处,测得顶端C的仰角为63.4°(如图2所示),求大楼部分楼体CD的高度约为多少米?(精确到1米)(参考数据:sin63.4°≈0.89,cos63.4°≈0.45,tan63.4°≈2.00,≈1.41,≈1.73)
参考答案与试题解析
一.选择题
1.【解答】解:过点C作CD⊥AB,交BA的延长线于点D,
∵∠BAC=120°,
∴∠DAC=180°﹣120°=60°,
∴∠ACD=30°,
∴AD=AC=3,
∴BD=AB+AD=7,
由勾股定理得,CD==3,
在Rt△BCD中,BC==2,
故选:B.
2.【解答】解:∵∠ACB=90°,D是AB的中点,CD=5,
∴AB=2CD=10,
∵AC=8,AB=10,
∴BC==6,
∴tanA===.
故选:C.
3.【解答】解:在Rt△ABC中,sinB=,
∴AC=ABsinB=10sin36°,
故选:C.
4.【解答】解:如图,
∵cosA=,
∴∠A=30°,
∵∠C=90°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠ABD=∠A=∠CBD=30°,
∴DB=DA=16,
∴BC=BDcos30°=16×=8,
故选:C.
5.【解答】解:由题意得,∠AOB=90°﹣60°=30°,
∴AB=OA=100(m),
故选:A.
6.【解答】解:作DN⊥BM于N,如图:
则HB=DN,DH=BN,
∵∠DCN=30°,CD=12米,
∴HB=DN=CD=6米,
CN=DN=6米,
∴DH=BN=BC+CN=10+6(米),
在Rt△ADH中,tan∠ADH==tan37°=0.75,
∴AH=0.75DH=0.75×(10+6)=15.15米,
∴AB=AH+HB=15.15+6≈21(米),
即楼房AB的高度约为21米.
故选:B.
7.【解答】解:延长AD、BC,两线交于O,
∵在Rt△ABO中,∠B=90°,tanA==,AB=3,
∴OB=4,
∵BC=2,
∴OC=OB﹣BC=4﹣2=2,
在Rt△ABO中,∠B=90°,AB=3,OB=4,由勾股定理得:AO=5,
∵∠ADC=90°,
∴∠ODC=90°=∠B,
∵∠O=∠O,
∴△ODC∽△OBA,
∴=,
∴=,
解得:DC=,
故选:C.
8.【解答】解:过B作BG⊥DE于G,BH⊥AE于H,如图:
则BG=AH+AE,GE=BH,
在Rt△ABF中,i=tan∠BAH=1:2.4=,
∴AH=2.4BH,
∴AB==2.6BH=26,
∴BH=10,AH=24,
∴BG=AH+AE=24+30=54,
在Rt△BGC中,∠CBG=45°,
∴CG=BG=54.
在Rt△ADE中,∠DAE=53°,
∴∠ADE=90°=53°=37°,
∵tan∠ADE==tan37°≈0.75,
∴DE=AE=40.
∴CD=CG+GE﹣DE=54+10﹣40=24(米);
即广告牌CD的高度约为24米;
故选:C.
9.【解答】解:过点F作FG⊥BD于G,FH⊥CD于H,如图所示:
则∠CFH=35°,四边形DGFH是矩形,
∴HF=DG,DH=FG,
∵斜坡AE的坡度为i=1:2.4,
∴设FG=x米,则EG=2.4x米,
在Rt△FGE中,由勾股定理得:EF2=FG2+EG2,
即:132=x2+(2.4x)2,
解得:x=5,
∴FG=5,EG=12,
∵∠CED=45°,
∴△CDE是等腰直角三角形,
∴CD=DE,
设CD=y米,则CH=(y﹣5)米,HF=(y+12)米,
Rt△CHF中,tan∠CFH=,
即tan35°=,则y﹣5=tan35°×(y+12),即y﹣5=0.7×(y+12),
解得:y≈44.7,
即建筑物的CD高度约为44.7米;
故选:D.
10.【解答】解:过A作AD⊥BC,垂足为D
在Rt△ABD中,∵∠BAD=30°,AD=30m,
∴BD=ADtan30°=30×=10(m),
在Rt△ACD中,∵∠CAD=60°,AD=30m,
∴CD=ADtan60°=30×=30(m),
∴BC=BD+CD=10+30=40(m),
即这栋高楼高度是40m.
故选:B.
二.填空题(共5小题)
11.【解答】解:如图,作AE⊥CD于E,则四边形ABCE为矩形,
∴CE=AB=1.5m,AE=BC,
在Rt△ACE中,tan∠CAE=,
∴AE===(m),
在Rt△ADE中,∵∠DAE=45°,
∴△ADE为等腰直角三角形,
∴DE=AE=m,
又∵CE=AB=1.5m,
∴CD=CE+DE=1.5+=(m),
答:建筑物CD的高度为m.
故答案为:.
12.【解答】解:由题意得,AB=50×14=700(米),
在Rt△ABC中,∠BAC=31°,sin∠BAC=,
∴BC=ABsin∠BAC=700sin31°(米),
故答案为:700sin31°米.
13.【解答】解:在Rt△ABC中,∠ACB=90°,∠A=30°,
∴BC=AB=×50=25(米),
故答案为:25.
14.【解答】解:过点B作BD⊥AC,垂足为D.
由题图知:AB=2,BC==2,
AC==2.
∵S△ABC=AB×CE=AC×BD,
∴×2×2=×2×BD,
∴BD=.
在Rt△BCD中,
sin∠ACB==
=.
故答案为:.
15.【解答】解:过A点作AD⊥BC于点D,
∵BC=3+0.3×2=3.6(m),AB=AC,
∴BD==1.8m,
∴=(m).
故答案为:.
三.解答题(共4小题)
16.【解答】解:(1)作CH⊥AB于H,如图所示:
由题意得:∠HCE=30°,CH∥BD,
∴∠CED=∠HCE=30°;
故答案为:30°;
(2)∵CH⊥AB,CD⊥BD,AB⊥BD,
∴四边形HBDC为矩形,
∴BD=CH,BH=CD,
由题意得,∠ACH=30°,∠CED=30°,
设CD=x
米,则AH=(30﹣x)米,
在Rt△AHC中,HC==(30﹣x),
则BD=CH=(30﹣x),
∴ED=(30﹣x)﹣9,
在Rt△CDE中,∠CED=30°,
∴ED=CD=x,
∴(30﹣x)﹣9=x,
解得,x=15﹣,
即立柱CD的高为(15﹣)米.
17.【解答】解:如图所示:
∵AD∥BC,
∴∠C=∠DAC=30°,
∵AB⊥BC,
∴∠ABC=90°,
∴BC=AB=1000≈1732.1(米),
即B,C之间的距离约为1732.1米.
18.【解答】解:如图,由题意可知PB=EC=1,
在Rt△APF与Rt△APE中,∠AFP=30°,∠AEP=45°,
设AP=x,则PE=x,,,
解得,
∴.
即该雕塑的高度为.
19.【解答】解:设楼高CE为x米,
∵在Rt△AEC中,∠CAE=45°,
∴AE=CE=x,
∵AB=16,
∴BE=x﹣16,
在Rt△CEB中,CE=BEtan63.4°≈2(x﹣16),
∴2(x﹣16)=x,
解得:x=32(米),
在Rt△DAE中,DE=AEtan30°=32×=,
∴CD=CE﹣DE=32﹣≈14(米),
答:大楼部分楼体CD的高度约为14米.
