苏科版九年级下册数学 7.6用锐角三角函数解决问题 同步测试(word含解析)
文档属性
| 名称 | 苏科版九年级下册数学 7.6用锐角三角函数解决问题 同步测试(word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 298.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 00:00:00 | ||
图片预览



文档简介
7.6用锐角三角函数解决问题
同步测试
一.选择题
1.如图,某商场一楼与二楼之间的电梯示意图.∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
A.m
B.4m
C.4m
D.8m
2.某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( )
A.20米
B.10米
C.10米
D.20米
3.如图是墙壁上在l1,l2两条平行线间边长为a的正方形瓷砖,该瓷砖与平行线的较大夹角为a,则两条平行线间的距离为( )
A.asinα
B.asinα+acosα
C.2acosα
D.asinα﹣acosα
4.重庆是一座著名的旅游城市,有着非常多的旅游景点,其中南山的大金鹰就是一个有名的人文景观.某周末,小李到大金鹰游玩,他从大金鹰底部的中心点A处水平向前走15米到点C,再沿坡度为1:0.75的斜坡CD走一段距离到达点D,在点D处观察测得大金鹰顶端点B的仰角为45°,再往前沿水平方向走45米到达点E,然后观察测得点B的仰角为22°,则大金鹰的高度AB约为( )(点A、B、C、D、E在同一平面内,参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
A.22米
B.41米
C.50米
D.62米
5.周末时,小明和妈妈在小区对面的山上玩儿,回家走到E点时,在E点处测得楼顶A的仰角为53°,沿着坡度i=1:2.4的山坡向下走了13米达到C处,再往前走了42米达到了B处,则小明家所住楼房的高度约为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.72
B.77
C.40.5
D.45.5
6.秀秀和山山在水平的地面上放风筝,某一时刻两人的风筝正好都停在对方的正上方,即此时AC⊥AB,DB⊥AB,两人之间的距离AB为120米,若两人的风筝线与水平线的夹角分别为a和β,则两人放出的风筝线AD与BC的长度和为(忽略两人的身高与手臂长度)( )米.
A.120tanα+120tanβ
B.+
C.120cosα+120cosβ
D.+
7.如图,一个坡角为15°的看台横截面上看旗杆CD,在这横截面上进行测量得到以下数据:在点A和点B处测得旗杆顶端的仰角分别为60°和30°,点A离地面高度为1米,且测得点A到点B的距离为8米,则旗杆的高度为( )
A.25米
B.24米
C.23米
D.26米
8.如图,某通信公司在一个坡度为2:1的山腰上建了一座垂直于水平面的5G信号通信塔AB,在距山脚C处水平距离24m的点D处测得通信塔底B处的仰角是30°,通信塔顶A处的仰角是45°.则通信塔的高度AB为( )(结果保留整数,参考数据:≈1.4,≈1.7)
A.17m
B.16m
C.14m
D.12m
9.如图,小明在C处看到西北方向上有一凉亭A,北偏东α°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=m米,则A、B两点相距( )
A.m(cosα+sinα)米
B.m(cosα﹣sinα)米
C.米
D.米
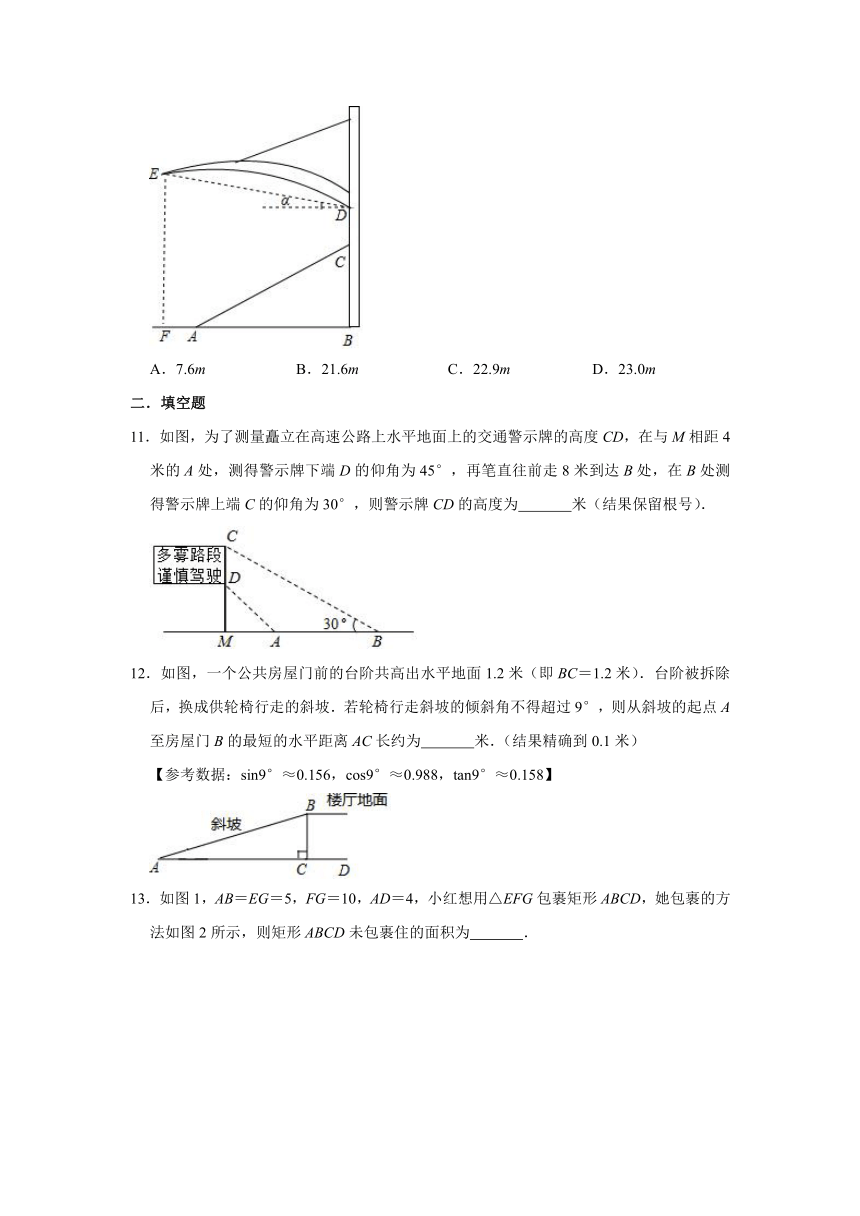
10.某体育看台侧面的示意图如图所示,观众区AC的坡度i为1:2.4,顶端C离水平地面AB的高度为10m,从顶棚的D处看E处的仰角α=18°30',竖直的立杆上C、D两点间的距离为4m,E处到观众区底端A处的水平距离AF为3m.顶棚的E处离地面的高度EF约为( )(sin18°30'≈0.32,tan18°30'≈0.33,结果精确到0.1m)
A.7.6m
B.21.6m
C.22.9m
D.23.0m
二.填空题
11.如图,为了测量矗立在高速公路上水平地面上的交通警示牌的高度CD,在与M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,则警示牌CD的高度为
米(结果保留根号).
12.如图,一个公共房屋门前的台阶共高出水平地面1.2米(即BC=1.2米).台阶被拆除后,换成供轮椅行走的斜坡.若轮椅行走斜坡的倾斜角不得超过9°,则从斜坡的起点A至房屋门B的最短的水平距离AC长约为
米.(结果精确到0.1米)
【参考数据:sin9°≈0.156,cos9°≈0.988,tan9°≈0.158】
13.如图1,AB=EG=5,FG=10,AD=4,小红想用△EFG包裹矩形ABCD,她包裹的方法如图2所示,则矩形ABCD未包裹住的面积为
.
14.如图,是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=88cm,宽AB=51cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距GC=15cm(点D,C,G,K在同一直线上).小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退
cm.(sin80°≈0.98,cos80°≈0.17,≈1.41,结果精确到个位)
15.如图,小丽的房间内有一张长200cm,高50cm的床靠墙摆放,在上方安装空调,空调下沿EF与墙垂直,出风口F离墙20cm,空调开启后,挡风板FG与EF夹角成136°,风沿FG方向吹出,为了让空调风不直接吹到床上,空调安装的高度(EC的长)至少为
cm.(精确到个位)(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
三.解答题
16.如图,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杄顶端E的俯角α是45°,旗杄底端D到大楼前梯坎底边的距离DC是10米,梯坎坡长BC是10米,梯坎坡度iBC=1:,求大楼AB的高.
17.如图是长沙九龙仓国际金融中心,位于长沙市黄兴路与解放路交汇处的东北角,投资160亿元人民币,总建筑面积达98万平方米,其主楼BC是目前湖南省第一高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,其高度为332米,在楼DE底端D点测得A的仰角为71.5°,在高楼DE的顶端E点测得B的仰角为37°,B,E之间的距离为200米.
(1)求九龙仓国际金融中心主楼BC的高度(精确到1米);
(2)求发射塔AB的高度(精确到1米);
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin71.5°≈0.95,cos71.5°≈0.32,tan71.5°≈3.00)
18.2018年,被“抖音”抖成“网红城市”大部分在西部地区,其中西安位居第二,该市青龙寺空海纪念碑游客明显高于去年同期.
如图,小丽和小明决定用所学知识测量纪念碑AB的高度,按照以下方式合作并记录所得数据:小丽从寺庙古塔的底端D点出发,沿直线步行5.6米到达E点,再沿坡度i=1:2.4的斜坡EF行走2.6米到达F点,最后沿直线步行12米到达纪念碑底部B点,小明从古塔DG的底端上行到离D点25.8米的顶端G点,从G点观察到纪念碑顶端A点的俯角为21°,若A、B、C、D、E、F、G在同一平面内,且B、F和C、E、D分别在同一水平线上,试求出纪念碑AB的高度.(精确到0.1米,参考数据:sin21°≈0.358,cos21°≈0.934,tan21°≈0.384)
参考答案
一.选择题
1.解:作CE⊥AB交AB
的延长线于E,
∵∠ABC=150°,
∴∠CBE=30°,
∴CE=BC=4m.
故选:C.
2.解:∵∠BDC=∠A+∠ABD,∠A=30°,∠BDC=60°,
∴∠ABD=60°﹣30°=30°,
∴∠A=∠ABD,
∴BD=AD=20米,
∴BC=BD?sin60°=10(米),
故选:C.
3.解:如图,过B作EF⊥l1于点E,EF与l2交于点F,则EF⊥l2,
∵四边形ABCD是正方形,
∴AB=BC=a,∠ABC=90°,
∴∠ABE+∠CBF=∠ABE+∠BAE=90°,
∴∠BAE=∠CBF,
∵∠AEB=∠BFC=90°,
∴△ABE≌△CFB(AAS),
∴BE=CF,
在Rt△BCF中,BF=a?sinα,CF=a?cosα,
∴BE=a?cosα,
∴EF=BE+BF=asinα+acosα,
即两条平行线间的距离为asinα+acosα,
故选:B.
4.解:延长ED交AB于F,则DF⊥AB,过D作DH⊥AC于H,
∵斜坡CD的坡度为1:0.75,
∴设DH=4x,CH=3x,
∴DF=AH=15+3x,AF=DH=4x,
在Rt△ABD中,∵∠BDF=45°,
∴BF=DF=15+3x,
∴EF=45+15+3x,
在Rt△BEF中,∵∠BEF=22°,
∴tan22°===0.40,
∴x=5,
∴AB=AF+BF=4x+15+3x=50(m),
故选:C.
5.解:过点E作EF⊥BC的延长线于点F,作EH⊥AB于点H,
在Rt△CEF中,∵i=EF:CF=,CE=13米,
∴EF=5米,CF=12米,
∴BH=EF=5米,HE=BF=BC+CF=42+12=54(米),
在Rt△AHE中,∵∠HAE=90°﹣53°=37°,
∴AH===72(米),
∴AB=AH+HB=72+5=77(米).
故选:B.
6.解:在Rt△ABD中,AD==(米);
在Rt△ABC中,BC==(米);
故两人放出的风筝线AD与BC的长度和为(+)米.
故选:D.
7.解:过A作AE⊥CD于E,AF⊥BC于点F,
∵∠BAC=180°﹣15°﹣60°=105°,∠ABC=45°
∴∠ACB=30°,
∵AB=8,
∴AF=BF=AB=8,
∴AC=2AF=16,
∵∠AEC=90°,∠ACE=30°,
∴CE=AC=24,
∵DE=1,
∴CD=24+1=25(米),
答:旗杆的高度为25米,
故选:A.
8.解:延长AB交DC延长线于点E,则AE⊥DC,
由题意知∠BDC=30°,∠ADE=45°,CD=24,
∵BC的坡度为2:1,
∴设CE=x、则BE=2x、DE=24+x,
在Rt△BDE中,tan∠BDE=,即,
解得:x=10,
∴DE=24+x=34,BE=2x=20,
在Rt△ADE中,AE=DE?tan∠ADE≈34×1=34,
则AB=AE﹣BE=34﹣20=14,
答:通信塔AB的大约高度约为14米.
故选:C.
9.解:过点C作CD⊥AB于D,如图所示:
由题意得:∠ACD=45°,∠DCB=α,
在Rt△BCD中,BC=m,
∴DB=BCsinα°=m?sinα(米),CD=BCcosα=m?cosα(米),
在Rt△ACD中,AD=CD=m?cosα(米),
∴AB=AD+DB=m(cosα+sinα)(米).
故选:A.
10.解:作CM⊥EF于M,DN⊥EF于N,
则四边形MFBC、MCDN为矩形,
∵观众区AC的坡度i为1:2.4,顶端C离水平地面AB的高度为10m,
∴AB=2.4BC=24(m),
∴MF=BC=10,MN=CD=4,DN=MC=BF=24+3=27,
在Rt△END中,tan∠EDN=,
则EN=DN?tan∠EDN=27×0.33≈8.91,
∴EF=EN+MN+MF=8.91+4+10≈22.9(m),
故选:C.
二.填空题
11.解:在Rt△ADM中,
∵AM=4,∠MAD=45°,
∴DM=AM=4,
∵AB=8,
∴MB=AM+AB=12,
在Rt△BCM中,∵∠MBC=30°,
∴MC=MBtan30°=4,
∴DC=MC﹣DM=(4﹣4)(米)
答:警示牌的高度CD为(4﹣4)米,
故答案为:(4﹣4).
12.解:在Rt△ABC中,∠A=9°,BC=1.2,
∴AC==≈7.6(米).
答:从斜坡的起点A至房屋门B的最短的水平距离AC长约为7.6米.
故答案为:7.6.
13.解:如图2,将矩形ABCD和Rt△ECF以AD为轴翻折,
∵Rt△GBE∽Rt△GB′C′,
∴=,即=,
解得:GB′=8,
∴S△B′C′G=?B′C′?B′G=×4×8=16,
故答案是:16.
14.解:过点F作FN⊥DK于N,过点E作EM⊥FN于M,过点E作EP⊥AB于点P,延长OB交MN于H,如图所示:
则四边形EPHM与四边形BCNH都为矩形,
∴PH=EM,
∵EF+FG=166cm,FG=100cm,
∴EF=66cm,
∵∠FGK=80°,
∴∠GFK=10°,
∵∠EFG=125°,
∴∠EFM=180°﹣125°﹣10°=45°,
∴△EFM是等腰直角三角形,
∴EM=EF=×66≈46.53,
∵AB=51,O为AB中点,
∴AO=BO=25.5,
∵PH=EM≈46.53,
∵GN=100?cos80°≈17,CG=15,
∴OH=25.5+15+17=57.5,OP=OH﹣PH=57.5﹣46.53≈11,
∴他应向前约11cm,
故答案为:11.
15.解:如图,连接FA,过F作FO⊥AD于点O,
则FO=ED,AO=200﹣20=180(cm),∠AFO=136°﹣90°=46°.
∵在Rt△FAO中,tan46°=,
∴FO==≈173(cm),
∴CE=CD+DE=50+173=223(cm).
故答案为:223.
三.解答题
16.解:如图,过点E作EF⊥AB于点F,作BG⊥CD于点G,
∵ED⊥CD,
∴四边形DEFG是矩形,
∴EF=DG,ED=FG,
根据题意可知:∠AEF=α=45°,
∴AF=EF,
∵坡度,
∴BG:CG=3:4,
设BG=3x,CG=4x,则BC=5x,
∴5x=10,
解得x=2,
∴CG=8,BG=6,
∴EF=DG=CG+CD=8+10=18,
∴AF=EF=18,
∵FG=ED=15,
∴FB=FG﹣BG=15﹣6=9,
∴AB=AF+FB=18+9=27(米).
答:大楼AB的高为27米.
17.解:(1)过点E作EF⊥AC于点F,
则四边形EFCD为矩形,
∴DE=CF=332米,
∵∠BEF=37°,BE=200米,
∴BF=BE?sin37°=200×0.60=120米,
∴BC=BF+CF=120+332=452米,
答:九龙仓国际金融中心主楼BC的高度为452米;
(2)∵BE=200米,∠BEF=37°,
∴EF=BE?cos37°=200×0.80=160米,
∴DC=160米,
在Rt△ADC中,
∵tan∠ADC=,
∴AC=160×3.00=480,
∴AB=AC﹣BC=480﹣452=28米,
故发射塔AB的高度为28米.
18.解:作GH⊥BA于H,FM⊥CD于M.则四边形BCMF,四边形CDGH是矩形.
在Rt△FEM中,FM:EM=1:2.4,EF=2.6米,
∴FM=BC=1米,EM=2.4米,CM=BF=12米,
∴CD=CM+EM+DE=12+2.4+5.6=20米,
∴GH=CD=20米,
在Rt△AGH中,AH=GH?tan21°=20×0.384≈7.68米,
∵CH=DG=25.8米,
∴AB=CH﹣BC﹣AH=25.8﹣1﹣7.68=17.12≈17.1(米),
同步测试
一.选择题
1.如图,某商场一楼与二楼之间的电梯示意图.∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
A.m
B.4m
C.4m
D.8m
2.某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( )
A.20米
B.10米
C.10米
D.20米
3.如图是墙壁上在l1,l2两条平行线间边长为a的正方形瓷砖,该瓷砖与平行线的较大夹角为a,则两条平行线间的距离为( )
A.asinα
B.asinα+acosα
C.2acosα
D.asinα﹣acosα
4.重庆是一座著名的旅游城市,有着非常多的旅游景点,其中南山的大金鹰就是一个有名的人文景观.某周末,小李到大金鹰游玩,他从大金鹰底部的中心点A处水平向前走15米到点C,再沿坡度为1:0.75的斜坡CD走一段距离到达点D,在点D处观察测得大金鹰顶端点B的仰角为45°,再往前沿水平方向走45米到达点E,然后观察测得点B的仰角为22°,则大金鹰的高度AB约为( )(点A、B、C、D、E在同一平面内,参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
A.22米
B.41米
C.50米
D.62米
5.周末时,小明和妈妈在小区对面的山上玩儿,回家走到E点时,在E点处测得楼顶A的仰角为53°,沿着坡度i=1:2.4的山坡向下走了13米达到C处,再往前走了42米达到了B处,则小明家所住楼房的高度约为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.72
B.77
C.40.5
D.45.5
6.秀秀和山山在水平的地面上放风筝,某一时刻两人的风筝正好都停在对方的正上方,即此时AC⊥AB,DB⊥AB,两人之间的距离AB为120米,若两人的风筝线与水平线的夹角分别为a和β,则两人放出的风筝线AD与BC的长度和为(忽略两人的身高与手臂长度)( )米.
A.120tanα+120tanβ
B.+
C.120cosα+120cosβ
D.+
7.如图,一个坡角为15°的看台横截面上看旗杆CD,在这横截面上进行测量得到以下数据:在点A和点B处测得旗杆顶端的仰角分别为60°和30°,点A离地面高度为1米,且测得点A到点B的距离为8米,则旗杆的高度为( )
A.25米
B.24米
C.23米
D.26米
8.如图,某通信公司在一个坡度为2:1的山腰上建了一座垂直于水平面的5G信号通信塔AB,在距山脚C处水平距离24m的点D处测得通信塔底B处的仰角是30°,通信塔顶A处的仰角是45°.则通信塔的高度AB为( )(结果保留整数,参考数据:≈1.4,≈1.7)
A.17m
B.16m
C.14m
D.12m
9.如图,小明在C处看到西北方向上有一凉亭A,北偏东α°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=m米,则A、B两点相距( )
A.m(cosα+sinα)米
B.m(cosα﹣sinα)米
C.米
D.米
10.某体育看台侧面的示意图如图所示,观众区AC的坡度i为1:2.4,顶端C离水平地面AB的高度为10m,从顶棚的D处看E处的仰角α=18°30',竖直的立杆上C、D两点间的距离为4m,E处到观众区底端A处的水平距离AF为3m.顶棚的E处离地面的高度EF约为( )(sin18°30'≈0.32,tan18°30'≈0.33,结果精确到0.1m)
A.7.6m
B.21.6m
C.22.9m
D.23.0m
二.填空题
11.如图,为了测量矗立在高速公路上水平地面上的交通警示牌的高度CD,在与M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,则警示牌CD的高度为
米(结果保留根号).
12.如图,一个公共房屋门前的台阶共高出水平地面1.2米(即BC=1.2米).台阶被拆除后,换成供轮椅行走的斜坡.若轮椅行走斜坡的倾斜角不得超过9°,则从斜坡的起点A至房屋门B的最短的水平距离AC长约为
米.(结果精确到0.1米)
【参考数据:sin9°≈0.156,cos9°≈0.988,tan9°≈0.158】
13.如图1,AB=EG=5,FG=10,AD=4,小红想用△EFG包裹矩形ABCD,她包裹的方法如图2所示,则矩形ABCD未包裹住的面积为
.
14.如图,是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=88cm,宽AB=51cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距GC=15cm(点D,C,G,K在同一直线上).小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退
cm.(sin80°≈0.98,cos80°≈0.17,≈1.41,结果精确到个位)
15.如图,小丽的房间内有一张长200cm,高50cm的床靠墙摆放,在上方安装空调,空调下沿EF与墙垂直,出风口F离墙20cm,空调开启后,挡风板FG与EF夹角成136°,风沿FG方向吹出,为了让空调风不直接吹到床上,空调安装的高度(EC的长)至少为
cm.(精确到个位)(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
三.解答题
16.如图,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杄顶端E的俯角α是45°,旗杄底端D到大楼前梯坎底边的距离DC是10米,梯坎坡长BC是10米,梯坎坡度iBC=1:,求大楼AB的高.
17.如图是长沙九龙仓国际金融中心,位于长沙市黄兴路与解放路交汇处的东北角,投资160亿元人民币,总建筑面积达98万平方米,其主楼BC是目前湖南省第一高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,其高度为332米,在楼DE底端D点测得A的仰角为71.5°,在高楼DE的顶端E点测得B的仰角为37°,B,E之间的距离为200米.
(1)求九龙仓国际金融中心主楼BC的高度(精确到1米);
(2)求发射塔AB的高度(精确到1米);
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin71.5°≈0.95,cos71.5°≈0.32,tan71.5°≈3.00)
18.2018年,被“抖音”抖成“网红城市”大部分在西部地区,其中西安位居第二,该市青龙寺空海纪念碑游客明显高于去年同期.
如图,小丽和小明决定用所学知识测量纪念碑AB的高度,按照以下方式合作并记录所得数据:小丽从寺庙古塔的底端D点出发,沿直线步行5.6米到达E点,再沿坡度i=1:2.4的斜坡EF行走2.6米到达F点,最后沿直线步行12米到达纪念碑底部B点,小明从古塔DG的底端上行到离D点25.8米的顶端G点,从G点观察到纪念碑顶端A点的俯角为21°,若A、B、C、D、E、F、G在同一平面内,且B、F和C、E、D分别在同一水平线上,试求出纪念碑AB的高度.(精确到0.1米,参考数据:sin21°≈0.358,cos21°≈0.934,tan21°≈0.384)
参考答案
一.选择题
1.解:作CE⊥AB交AB
的延长线于E,
∵∠ABC=150°,
∴∠CBE=30°,
∴CE=BC=4m.
故选:C.
2.解:∵∠BDC=∠A+∠ABD,∠A=30°,∠BDC=60°,
∴∠ABD=60°﹣30°=30°,
∴∠A=∠ABD,
∴BD=AD=20米,
∴BC=BD?sin60°=10(米),
故选:C.
3.解:如图,过B作EF⊥l1于点E,EF与l2交于点F,则EF⊥l2,
∵四边形ABCD是正方形,
∴AB=BC=a,∠ABC=90°,
∴∠ABE+∠CBF=∠ABE+∠BAE=90°,
∴∠BAE=∠CBF,
∵∠AEB=∠BFC=90°,
∴△ABE≌△CFB(AAS),
∴BE=CF,
在Rt△BCF中,BF=a?sinα,CF=a?cosα,
∴BE=a?cosα,
∴EF=BE+BF=asinα+acosα,
即两条平行线间的距离为asinα+acosα,
故选:B.
4.解:延长ED交AB于F,则DF⊥AB,过D作DH⊥AC于H,
∵斜坡CD的坡度为1:0.75,
∴设DH=4x,CH=3x,
∴DF=AH=15+3x,AF=DH=4x,
在Rt△ABD中,∵∠BDF=45°,
∴BF=DF=15+3x,
∴EF=45+15+3x,
在Rt△BEF中,∵∠BEF=22°,
∴tan22°===0.40,
∴x=5,
∴AB=AF+BF=4x+15+3x=50(m),
故选:C.
5.解:过点E作EF⊥BC的延长线于点F,作EH⊥AB于点H,
在Rt△CEF中,∵i=EF:CF=,CE=13米,
∴EF=5米,CF=12米,
∴BH=EF=5米,HE=BF=BC+CF=42+12=54(米),
在Rt△AHE中,∵∠HAE=90°﹣53°=37°,
∴AH===72(米),
∴AB=AH+HB=72+5=77(米).
故选:B.
6.解:在Rt△ABD中,AD==(米);
在Rt△ABC中,BC==(米);
故两人放出的风筝线AD与BC的长度和为(+)米.
故选:D.
7.解:过A作AE⊥CD于E,AF⊥BC于点F,
∵∠BAC=180°﹣15°﹣60°=105°,∠ABC=45°
∴∠ACB=30°,
∵AB=8,
∴AF=BF=AB=8,
∴AC=2AF=16,
∵∠AEC=90°,∠ACE=30°,
∴CE=AC=24,
∵DE=1,
∴CD=24+1=25(米),
答:旗杆的高度为25米,
故选:A.
8.解:延长AB交DC延长线于点E,则AE⊥DC,
由题意知∠BDC=30°,∠ADE=45°,CD=24,
∵BC的坡度为2:1,
∴设CE=x、则BE=2x、DE=24+x,
在Rt△BDE中,tan∠BDE=,即,
解得:x=10,
∴DE=24+x=34,BE=2x=20,
在Rt△ADE中,AE=DE?tan∠ADE≈34×1=34,
则AB=AE﹣BE=34﹣20=14,
答:通信塔AB的大约高度约为14米.
故选:C.
9.解:过点C作CD⊥AB于D,如图所示:
由题意得:∠ACD=45°,∠DCB=α,
在Rt△BCD中,BC=m,
∴DB=BCsinα°=m?sinα(米),CD=BCcosα=m?cosα(米),
在Rt△ACD中,AD=CD=m?cosα(米),
∴AB=AD+DB=m(cosα+sinα)(米).
故选:A.
10.解:作CM⊥EF于M,DN⊥EF于N,
则四边形MFBC、MCDN为矩形,
∵观众区AC的坡度i为1:2.4,顶端C离水平地面AB的高度为10m,
∴AB=2.4BC=24(m),
∴MF=BC=10,MN=CD=4,DN=MC=BF=24+3=27,
在Rt△END中,tan∠EDN=,
则EN=DN?tan∠EDN=27×0.33≈8.91,
∴EF=EN+MN+MF=8.91+4+10≈22.9(m),
故选:C.
二.填空题
11.解:在Rt△ADM中,
∵AM=4,∠MAD=45°,
∴DM=AM=4,
∵AB=8,
∴MB=AM+AB=12,
在Rt△BCM中,∵∠MBC=30°,
∴MC=MBtan30°=4,
∴DC=MC﹣DM=(4﹣4)(米)
答:警示牌的高度CD为(4﹣4)米,
故答案为:(4﹣4).
12.解:在Rt△ABC中,∠A=9°,BC=1.2,
∴AC==≈7.6(米).
答:从斜坡的起点A至房屋门B的最短的水平距离AC长约为7.6米.
故答案为:7.6.
13.解:如图2,将矩形ABCD和Rt△ECF以AD为轴翻折,
∵Rt△GBE∽Rt△GB′C′,
∴=,即=,
解得:GB′=8,
∴S△B′C′G=?B′C′?B′G=×4×8=16,
故答案是:16.
14.解:过点F作FN⊥DK于N,过点E作EM⊥FN于M,过点E作EP⊥AB于点P,延长OB交MN于H,如图所示:
则四边形EPHM与四边形BCNH都为矩形,
∴PH=EM,
∵EF+FG=166cm,FG=100cm,
∴EF=66cm,
∵∠FGK=80°,
∴∠GFK=10°,
∵∠EFG=125°,
∴∠EFM=180°﹣125°﹣10°=45°,
∴△EFM是等腰直角三角形,
∴EM=EF=×66≈46.53,
∵AB=51,O为AB中点,
∴AO=BO=25.5,
∵PH=EM≈46.53,
∵GN=100?cos80°≈17,CG=15,
∴OH=25.5+15+17=57.5,OP=OH﹣PH=57.5﹣46.53≈11,
∴他应向前约11cm,
故答案为:11.
15.解:如图,连接FA,过F作FO⊥AD于点O,
则FO=ED,AO=200﹣20=180(cm),∠AFO=136°﹣90°=46°.
∵在Rt△FAO中,tan46°=,
∴FO==≈173(cm),
∴CE=CD+DE=50+173=223(cm).
故答案为:223.
三.解答题
16.解:如图,过点E作EF⊥AB于点F,作BG⊥CD于点G,
∵ED⊥CD,
∴四边形DEFG是矩形,
∴EF=DG,ED=FG,
根据题意可知:∠AEF=α=45°,
∴AF=EF,
∵坡度,
∴BG:CG=3:4,
设BG=3x,CG=4x,则BC=5x,
∴5x=10,
解得x=2,
∴CG=8,BG=6,
∴EF=DG=CG+CD=8+10=18,
∴AF=EF=18,
∵FG=ED=15,
∴FB=FG﹣BG=15﹣6=9,
∴AB=AF+FB=18+9=27(米).
答:大楼AB的高为27米.
17.解:(1)过点E作EF⊥AC于点F,
则四边形EFCD为矩形,
∴DE=CF=332米,
∵∠BEF=37°,BE=200米,
∴BF=BE?sin37°=200×0.60=120米,
∴BC=BF+CF=120+332=452米,
答:九龙仓国际金融中心主楼BC的高度为452米;
(2)∵BE=200米,∠BEF=37°,
∴EF=BE?cos37°=200×0.80=160米,
∴DC=160米,
在Rt△ADC中,
∵tan∠ADC=,
∴AC=160×3.00=480,
∴AB=AC﹣BC=480﹣452=28米,
故发射塔AB的高度为28米.
18.解:作GH⊥BA于H,FM⊥CD于M.则四边形BCMF,四边形CDGH是矩形.
在Rt△FEM中,FM:EM=1:2.4,EF=2.6米,
∴FM=BC=1米,EM=2.4米,CM=BF=12米,
∴CD=CM+EM+DE=12+2.4+5.6=20米,
∴GH=CD=20米,
在Rt△AGH中,AH=GH?tan21°=20×0.384≈7.68米,
∵CH=DG=25.8米,
∴AB=CH﹣BC﹣AH=25.8﹣1﹣7.68=17.12≈17.1(米),
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
