新人教版数学七年级上 4.3.2余角与补角(第三课时)
文档属性
| 名称 | 新人教版数学七年级上 4.3.2余角与补角(第三课时) |

|
|
| 格式 | rar | ||
| 文件大小 | 510.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-13 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
4.3.2余角与补角
一、余角和补角的概念
互为余角:如果两个角的和等于90°(直角),就说这两个角互为余角,其中一个角是另一个角的余角。
互为补角:如果两个角的和等于180°(平角),就说这两个角互为补角,其中一个角是另一个角的补角。
(1)定义中的“互为”一词如何理解?
(2)互补、互余的两角是否一定有公共顶点或公共边?
(3)∠1和∠2互补,除用符号语言表示为∠1+∠2= 180°外,用符号语言还可以表示为 ∠1= 180°- ∠2或∠2= 180°- ∠1
二、提问答疑,理解定义
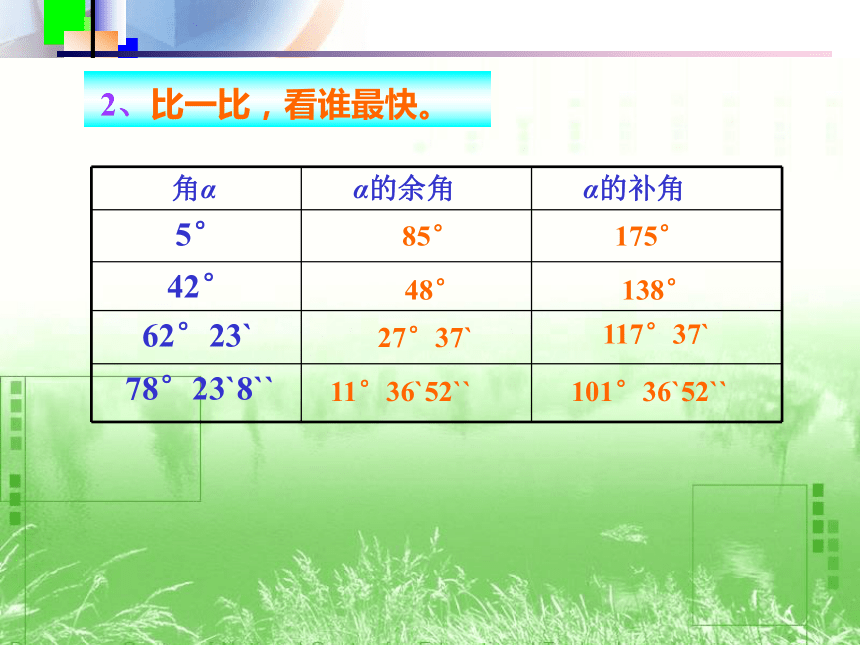
角α α的余角 α的补角
5°
42°
62°23`
78°23`8``
48°
85°
175°
138°
27°37`
117°37`
11°36`52``
101°36`52``
2、比一比,看谁最快。
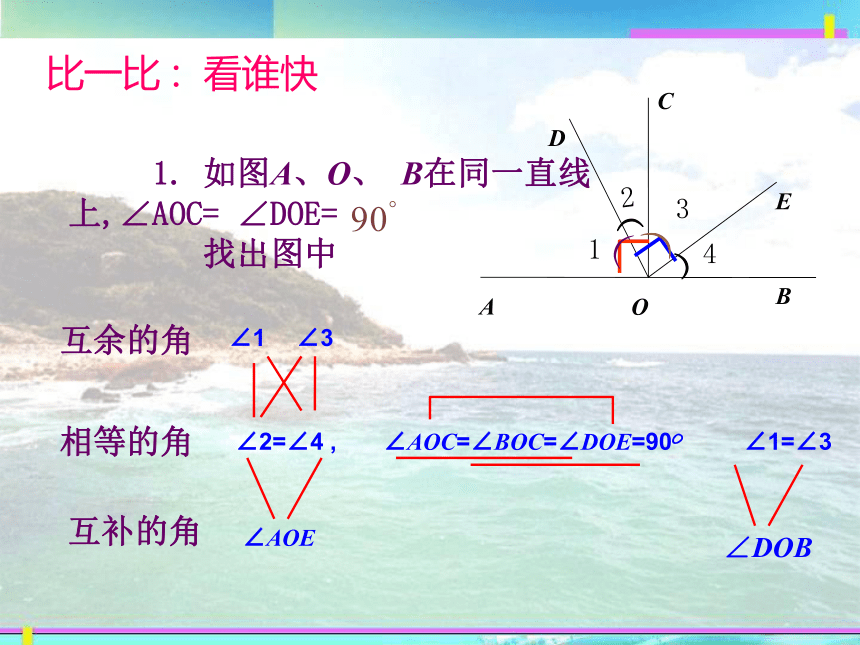
比一比 : 看谁快
互补的角
1. 如图A、O、 B在同一直线上,∠AOC= ∠DOE=
找出图中
∠2=∠4 , ∠AOC=∠BOC=∠DOE=900 ∠1=∠3
互余的角
相等的角
∠1
∠3
∠AOE
∠DOB
C
A
O
B
D
E
)
)
(
)
4
3
1
2
请注意:用代数方法解决几何问题是常 用的一种策略
试一试:看谁会
2. 如图A、O、 B在同一直线上, ∠AOC= ∠DOE=90°
若∠1= 2∠3,求:∠2的度数
解:设∠3 =x,则∠1=2x
∵∠1+∠DOE+∠3=1800
答: ∠2的度数为30度
A
O
C
B
D
E
)
)
(
3
1
2
∴∠2=∠3
(同角的余角相等)
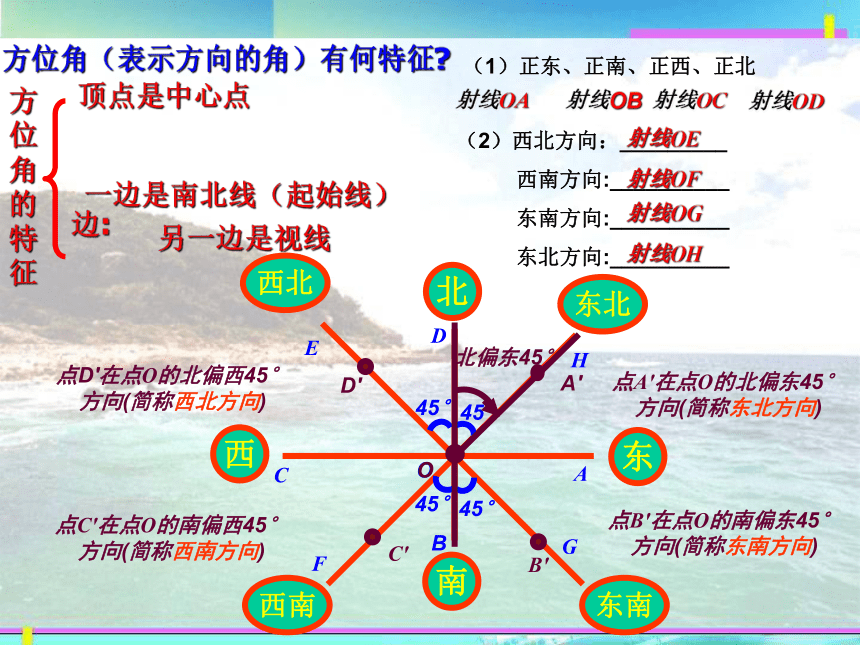
(1)正东、正南、正西、正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
射线OB
射线OC
射线OD
射线OE
射线OF
射线OG
射线OH
东
南
西
北
西北
西南
东南
东北
O
A
B
C
D
E
F
H
G
45°
45°
45°
45°
A′
方位角(表示方向的角)有何特征
方位角的特征
顶点是中心点
边:
另一边是视线
一边是南北线(起始线)
北偏东45°
O
点A′在点O的北偏东45°方向(简称东北方向)
B′
C′
D′
点B′在点O的南偏东45°方向(简称东南方向)
点C′在点O的南偏西45°方向(简称西南方向)
点D′在点O的北偏西45°方向(简称西北方向)
●
B
40°
东
南
西
北
40°
A
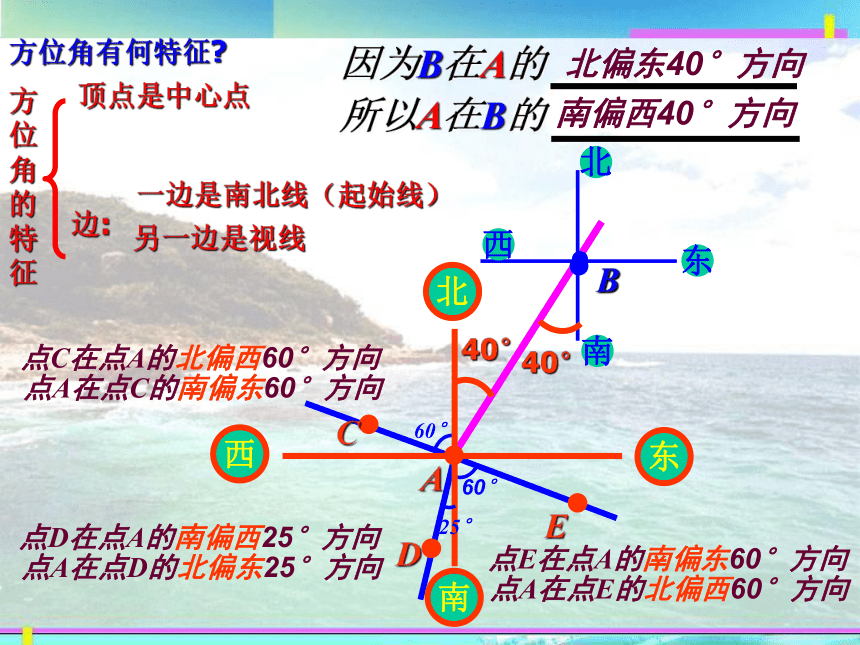
因为B在A的
所以A在B的
B
南偏西40°方向
北偏东40°方向
E
60°
C
60°
点C在点A的北偏西60°方向
点A在点C的南偏东60°方向
点D在点A的南偏西25°方向
点A在点D的北偏东25°方向
点E在点A的南偏东60°方向
点A在点E的北偏西60°方向
东
南
西
北
方位角有何特征
方位角的特征
边:
另一边是视线
顶点是中心点
一边是南北线(起始线)
D
25°
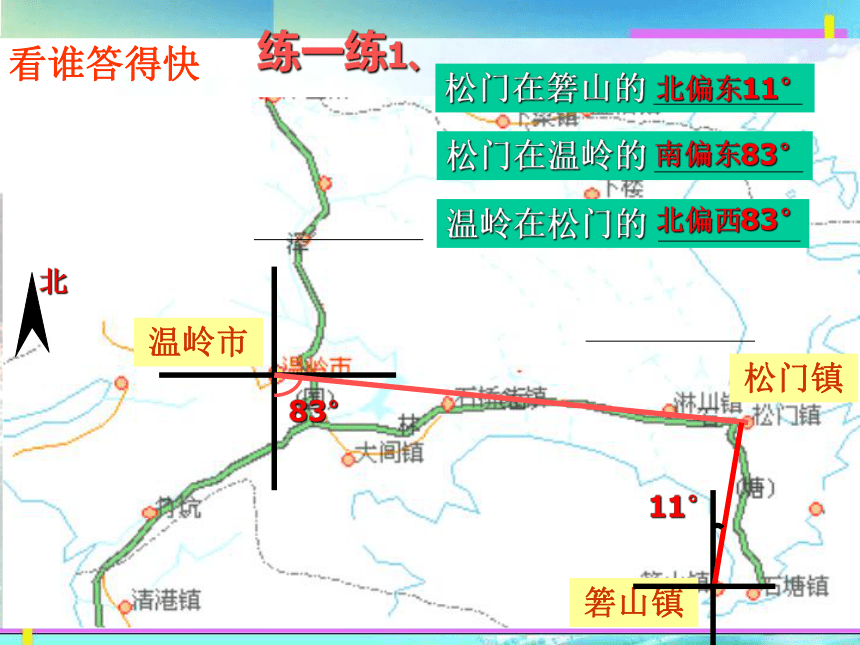
练一练1、
松门在箬山的
松门在温岭的
温岭在松门的
北
83°
11°
南偏东83°
北偏西83°
北偏东11°
松门镇
箬山镇
温岭市
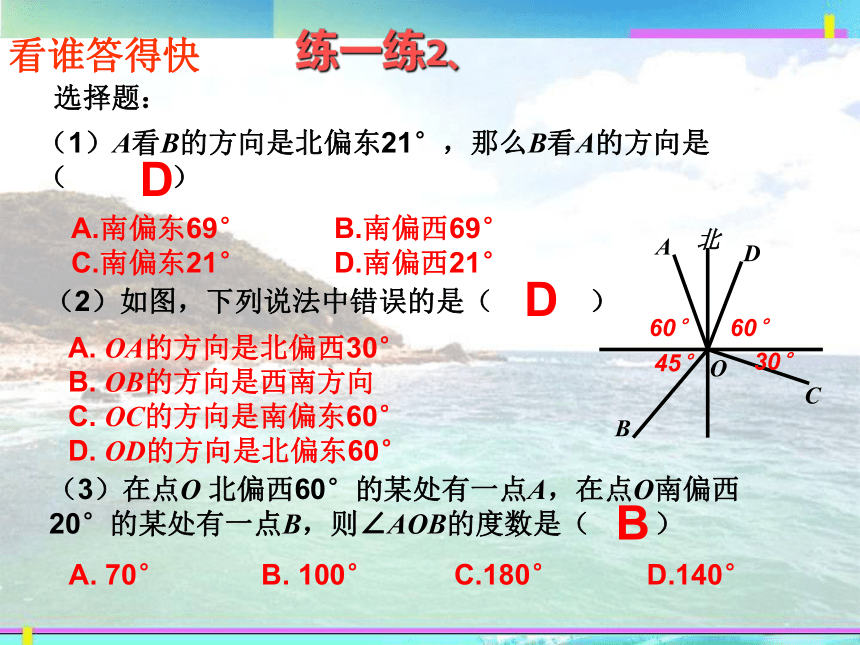
看谁答得快
(1)A看B的方向是北偏东21°,那么B看A的方向是( )
A.南偏东69° B.南偏西69° C.南偏东21° D.南偏西21°
(2)如图,下列说法中错误的是( )
A. OA的方向是北偏西30° B. OB的方向是西南方向 C. OC的方向是南偏东60° D. OD的方向是北偏东60°
北
A
B
C
D
45°
60°
60°
30°
O
(3)在点O 北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是( )
A. 70° B. 100° C.180° D.140°
D
D
B
选择题:
练一练2、
看谁答得快
(1)电视塔在学校的东北方向,那么学校在电视塔的 ______ 方向.
(2)已知点O在点A的南偏东65 °方向,那么点A应在点O的 ( )
A.南偏东65 °方向; B. 北偏东65 °方向;
C.北偏西65 °方向; D.北偏西25 °方向;
(3)如图,邮局和商店分别在学校的北偏西方向,邮局又在商店的北偏东方向.那么,图中A点应该是________,B点应该是_______,C点应该是______.
.A
.B
.C
西南
C
邮局
商店
学校
北
南
西
东
练一练3、
看谁答得快
杨利伟乘坐“神州”五号遨游太空时,我国当时派出远望一号至四号船队,跟踪检测,其中远望一、二号停在太平洋洋面上,某一时刻,分别测得杨利伟在北偏东60°和北偏东30°的方向,你能在下图中画出当时杨利伟所处的位置吗?
●
●
远望一号
远望二号
另一时刻,杨利伟在“神州五号”上测得“远望一号”“远望二号”在他的南偏西70°和南偏西20°的方向,你能在下图中画出此时杨利伟所处的位置吗?
你知道他是谁
看谁画得快
A
西
东
北
南
西
东
北
南
西
东
北
南
70°
20°
B
南偏西70°
南偏西20°
南偏西70°
南偏西20°
北
南
西
东
灯塔A在灯塔B的南偏西60 ° ,A、B两灯塔
相距20海里.现有一艘轮船C在灯塔B的正北
方向、 灯塔A的北偏东30 °方向.试画图确定 轮船
的位置(每10海里用1厘米长的线段表示)
解:
.B
A.
.C
∴如图的点C就是轮船 的 位置.
20海里
30°
60°
看谁画得快
北
南
西
东
例1:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
O
●
● A
60°
答:射线OA的方向就是南偏东60°,即灯塔A所在的方向。
● B
● D
射线OB的方向就是北偏东40°,即客轮B所在的方向。
C ●
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向。
射线OD的方向就是南偏西45°,即海岛D所在的方向。
45°
看谁画得快
北
南
西
东
(1)教师宿舍在校门口的北偏西15°的方向,试画出教师宿舍方向的射线.
北
●
●
●
●
●
●
●
校门
教学楼
办公楼
综合楼
操场
餐厅
学生宿舍
学校平面示意图
练一练4、
在
(2)教学楼在校门口的
方向.
看谁画得快
南偏西60°
北
南
西
东
(3)学校、公园和商店在平面图上的标点分别是A、B、C
三点.若公园在学校的南偏西42 ° ,商店在学校的
北偏东50 ° ,请画出图形,并求∠BAC.
.B
C.
42 °
50 °
解:∠BAC=
42°+90 °+40 °=172 °
A.
练一练4、
看谁画得快
例2.应用题
一艘渔船从O 点沿北偏东30°的方向以8千米/时的速度行驶3小时到达A 处后,接到风浪警报,欲立即调头以16千米/时的速度向正西方向行驶,争取1.5小时到达小岛B 处.A、B两处的距离是多少?B处在O点北偏西多少度?O、B两点的距离是多少?
看谁算得快
北
南
西
东
A
B
8×3=24
30°
30°
16×1.5=24
解:OA=8×3=24(千米)
AB=16×1.5=24(千米)
量得B处在O点北偏西30°
量得O、B两点的距离是24千米。
O
小明从点A出发向北偏西50°方向走了3米,到达点B,小强从点A出发向南偏西40°方向走了4米,试画图确定出A、B、C三点的位置(用1厘米表示3米)。 (1)从图上量出B点到C点的实际距离, (2)通过计算,猜想AB2、AC2 、BC2之间有什么关系
东
南
西
北
50°
40°
练一练5、
看谁量得快
3
4
5
A
B
C
解:(1)量得BC=5厘米,表示实际距离5米。
(2)AB 2 = 3 2 = 9,AC 2 = 4 2 = 16
BC 2 = 5 2 = 25
∵AB 2 + BC 2 =9+16=25
∵AB 2 + BC 2 = BC 2
● 本节课你学到了哪些知识?
● 通过这节课的学习后,你有什么感受
畅所欲言
●你还有什么疑问吗
2、课外作业:测一下你在教室的座位在你们班长座位的哪个方向?
1、作业本(2)第28页
下课了!
游戏:折一折 算一算
1、 如图1,把三角形的一角折叠得到折痕EF,
已知:∠EFB= ,求: ∠EFC的度数
(
(
F
E
D
C
B
A
如图1
A
(
F
B
D
E
(C)
(
G
如图2
2、如图2所示折叠,已知∠EFG= ,求: ∠BFE的度数
4.3.2余角与补角
一、余角和补角的概念
互为余角:如果两个角的和等于90°(直角),就说这两个角互为余角,其中一个角是另一个角的余角。
互为补角:如果两个角的和等于180°(平角),就说这两个角互为补角,其中一个角是另一个角的补角。
(1)定义中的“互为”一词如何理解?
(2)互补、互余的两角是否一定有公共顶点或公共边?
(3)∠1和∠2互补,除用符号语言表示为∠1+∠2= 180°外,用符号语言还可以表示为 ∠1= 180°- ∠2或∠2= 180°- ∠1
二、提问答疑,理解定义
角α α的余角 α的补角
5°
42°
62°23`
78°23`8``
48°
85°
175°
138°
27°37`
117°37`
11°36`52``
101°36`52``
2、比一比,看谁最快。
比一比 : 看谁快
互补的角
1. 如图A、O、 B在同一直线上,∠AOC= ∠DOE=
找出图中
∠2=∠4 , ∠AOC=∠BOC=∠DOE=900 ∠1=∠3
互余的角
相等的角
∠1
∠3
∠AOE
∠DOB
C
A
O
B
D
E
)
)
(
)
4
3
1
2
请注意:用代数方法解决几何问题是常 用的一种策略
试一试:看谁会
2. 如图A、O、 B在同一直线上, ∠AOC= ∠DOE=90°
若∠1= 2∠3,求:∠2的度数
解:设∠3 =x,则∠1=2x
∵∠1+∠DOE+∠3=1800
答: ∠2的度数为30度
A
O
C
B
D
E
)
)
(
3
1
2
∴∠2=∠3
(同角的余角相等)
(1)正东、正南、正西、正北
(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OA
射线OB
射线OC
射线OD
射线OE
射线OF
射线OG
射线OH
东
南
西
北
西北
西南
东南
东北
O
A
B
C
D
E
F
H
G
45°
45°
45°
45°
A′
方位角(表示方向的角)有何特征
方位角的特征
顶点是中心点
边:
另一边是视线
一边是南北线(起始线)
北偏东45°
O
点A′在点O的北偏东45°方向(简称东北方向)
B′
C′
D′
点B′在点O的南偏东45°方向(简称东南方向)
点C′在点O的南偏西45°方向(简称西南方向)
点D′在点O的北偏西45°方向(简称西北方向)
●
B
40°
东
南
西
北
40°
A
因为B在A的
所以A在B的
B
南偏西40°方向
北偏东40°方向
E
60°
C
60°
点C在点A的北偏西60°方向
点A在点C的南偏东60°方向
点D在点A的南偏西25°方向
点A在点D的北偏东25°方向
点E在点A的南偏东60°方向
点A在点E的北偏西60°方向
东
南
西
北
方位角有何特征
方位角的特征
边:
另一边是视线
顶点是中心点
一边是南北线(起始线)
D
25°
练一练1、
松门在箬山的
松门在温岭的
温岭在松门的
北
83°
11°
南偏东83°
北偏西83°
北偏东11°
松门镇
箬山镇
温岭市
看谁答得快
(1)A看B的方向是北偏东21°,那么B看A的方向是( )
A.南偏东69° B.南偏西69° C.南偏东21° D.南偏西21°
(2)如图,下列说法中错误的是( )
A. OA的方向是北偏西30° B. OB的方向是西南方向 C. OC的方向是南偏东60° D. OD的方向是北偏东60°
北
A
B
C
D
45°
60°
60°
30°
O
(3)在点O 北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是( )
A. 70° B. 100° C.180° D.140°
D
D
B
选择题:
练一练2、
看谁答得快
(1)电视塔在学校的东北方向,那么学校在电视塔的 ______ 方向.
(2)已知点O在点A的南偏东65 °方向,那么点A应在点O的 ( )
A.南偏东65 °方向; B. 北偏东65 °方向;
C.北偏西65 °方向; D.北偏西25 °方向;
(3)如图,邮局和商店分别在学校的北偏西方向,邮局又在商店的北偏东方向.那么,图中A点应该是________,B点应该是_______,C点应该是______.
.A
.B
.C
西南
C
邮局
商店
学校
北
南
西
东
练一练3、
看谁答得快
杨利伟乘坐“神州”五号遨游太空时,我国当时派出远望一号至四号船队,跟踪检测,其中远望一、二号停在太平洋洋面上,某一时刻,分别测得杨利伟在北偏东60°和北偏东30°的方向,你能在下图中画出当时杨利伟所处的位置吗?
●
●
远望一号
远望二号
另一时刻,杨利伟在“神州五号”上测得“远望一号”“远望二号”在他的南偏西70°和南偏西20°的方向,你能在下图中画出此时杨利伟所处的位置吗?
你知道他是谁
看谁画得快
A
西
东
北
南
西
东
北
南
西
东
北
南
70°
20°
B
南偏西70°
南偏西20°
南偏西70°
南偏西20°
北
南
西
东
灯塔A在灯塔B的南偏西60 ° ,A、B两灯塔
相距20海里.现有一艘轮船C在灯塔B的正北
方向、 灯塔A的北偏东30 °方向.试画图确定 轮船
的位置(每10海里用1厘米长的线段表示)
解:
.B
A.
.C
∴如图的点C就是轮船 的 位置.
20海里
30°
60°
看谁画得快
北
南
西
东
例1:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
O
●
● A
60°
答:射线OA的方向就是南偏东60°,即灯塔A所在的方向。
● B
● D
射线OB的方向就是北偏东40°,即客轮B所在的方向。
C ●
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向。
射线OD的方向就是南偏西45°,即海岛D所在的方向。
45°
看谁画得快
北
南
西
东
(1)教师宿舍在校门口的北偏西15°的方向,试画出教师宿舍方向的射线.
北
●
●
●
●
●
●
●
校门
教学楼
办公楼
综合楼
操场
餐厅
学生宿舍
学校平面示意图
练一练4、
在
(2)教学楼在校门口的
方向.
看谁画得快
南偏西60°
北
南
西
东
(3)学校、公园和商店在平面图上的标点分别是A、B、C
三点.若公园在学校的南偏西42 ° ,商店在学校的
北偏东50 ° ,请画出图形,并求∠BAC.
.B
C.
42 °
50 °
解:∠BAC=
42°+90 °+40 °=172 °
A.
练一练4、
看谁画得快
例2.应用题
一艘渔船从O 点沿北偏东30°的方向以8千米/时的速度行驶3小时到达A 处后,接到风浪警报,欲立即调头以16千米/时的速度向正西方向行驶,争取1.5小时到达小岛B 处.A、B两处的距离是多少?B处在O点北偏西多少度?O、B两点的距离是多少?
看谁算得快
北
南
西
东
A
B
8×3=24
30°
30°
16×1.5=24
解:OA=8×3=24(千米)
AB=16×1.5=24(千米)
量得B处在O点北偏西30°
量得O、B两点的距离是24千米。
O
小明从点A出发向北偏西50°方向走了3米,到达点B,小强从点A出发向南偏西40°方向走了4米,试画图确定出A、B、C三点的位置(用1厘米表示3米)。 (1)从图上量出B点到C点的实际距离, (2)通过计算,猜想AB2、AC2 、BC2之间有什么关系
东
南
西
北
50°
40°
练一练5、
看谁量得快
3
4
5
A
B
C
解:(1)量得BC=5厘米,表示实际距离5米。
(2)AB 2 = 3 2 = 9,AC 2 = 4 2 = 16
BC 2 = 5 2 = 25
∵AB 2 + BC 2 =9+16=25
∵AB 2 + BC 2 = BC 2
● 本节课你学到了哪些知识?
● 通过这节课的学习后,你有什么感受
畅所欲言
●你还有什么疑问吗
2、课外作业:测一下你在教室的座位在你们班长座位的哪个方向?
1、作业本(2)第28页
下课了!
游戏:折一折 算一算
1、 如图1,把三角形的一角折叠得到折痕EF,
已知:∠EFB= ,求: ∠EFC的度数
(
(
F
E
D
C
B
A
如图1
A
(
F
B
D
E
(C)
(
G
如图2
2、如图2所示折叠,已知∠EFG= ,求: ∠BFE的度数
