广东省平远县高级中学校2021届高三上学期第五次月考(1月)数学试题 Word版含答案
文档属性
| 名称 | 广东省平远县高级中学校2021届高三上学期第五次月考(1月)数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 765.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 18:06:03 | ||
图片预览



文档简介
____________________________________________________________________________________________
平远县高级中学校2021届高三上学期第五次月考
数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。考试时间120分钟,满分150分。考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效。交卷时只交答题卡。
第一部分选择题(共60分)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.
1.已知集合,若,则()
A.-1 B.0 C.1 D.2
2.在复平面内,复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.己知向量,,著,则( )
A.10 B.2 C. D.
4.下列判断正确的是( )
A.若命题为真命题,命题为假命题,则命题“”为真命题
B.命题“”的否定是“”
C.“”是“”的充分不必要条件
D.命题“若,则”的否命题为“若,则”
5.已知,则的大小关系是( )
A. B. C. D.
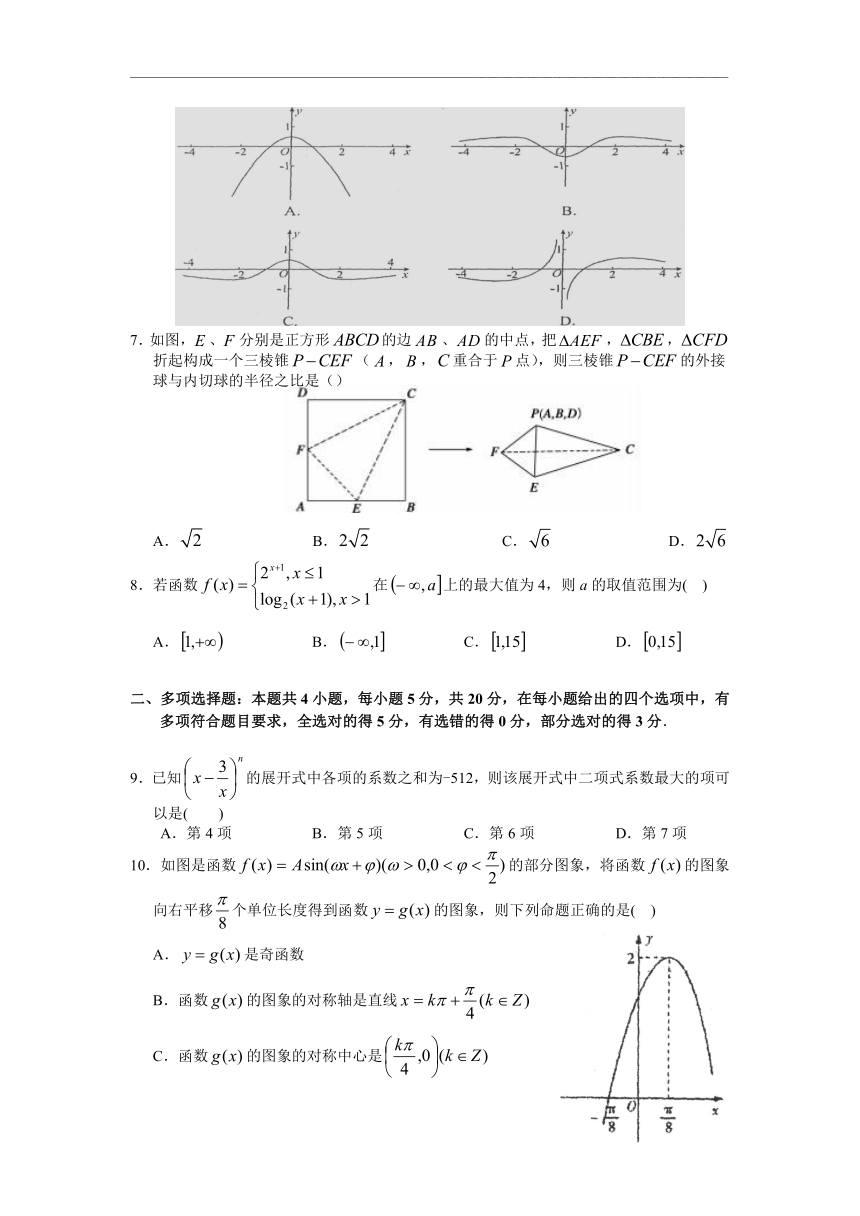
6.函数的大致图象为( )
7.如图,、分别是正方形的边、的中点,把,,折起构成一个三棱锥(,,重合于点),则三棱锥的外接球与内切球的半径之比是()
A. B. C. D.
8.若函数在上的最大值为4,则a的取值范围为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目要求,全选对的得5分,有选错的得0分,部分选对的得3分.
9.已知的展开式中各项的系数之和为-512,则该展开式中二项式系数最大的项可以是( )
A.第4项 B.第5项 C.第6项 D.第7项
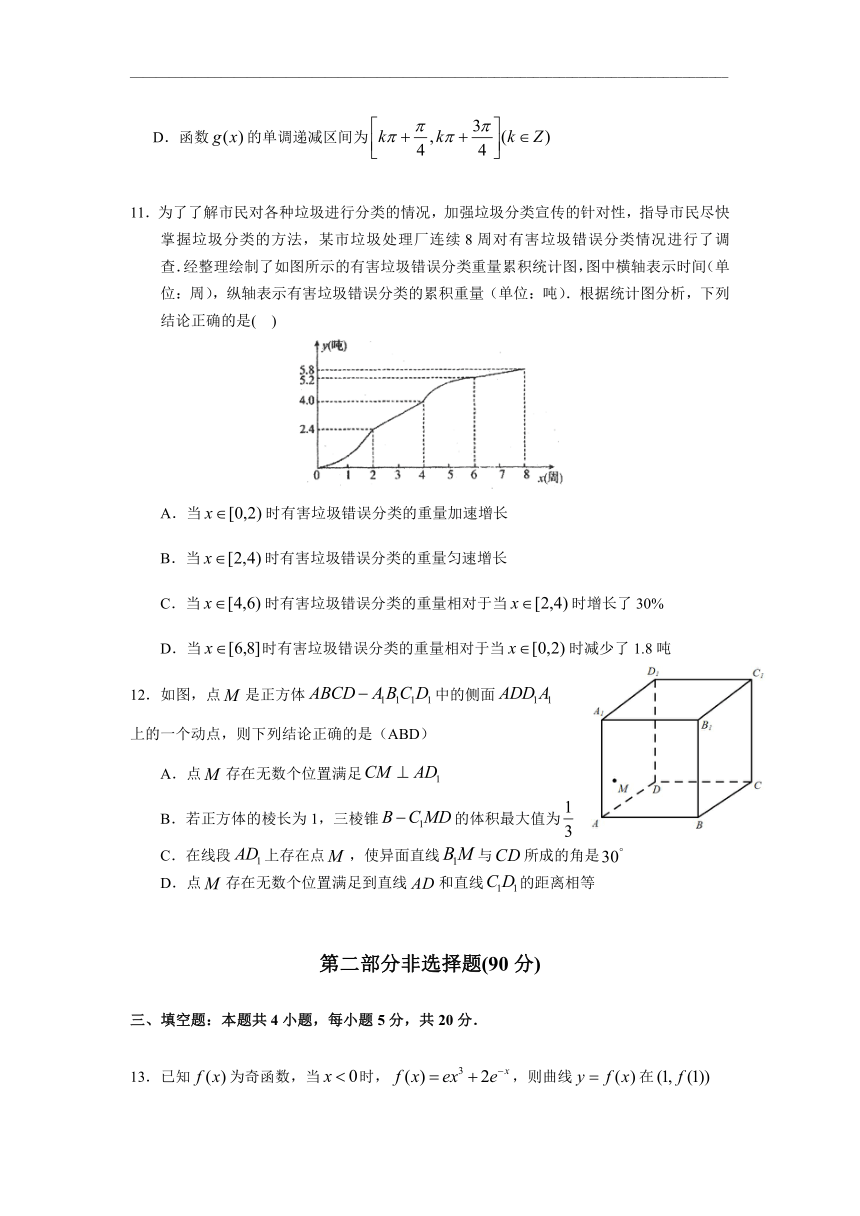
10.如图是函数的部分图象,将函数的图象向右平移个单位长度得到函数的图象,则下列命题正确的是( )
A.是奇函数
B.函数的图象的对称轴是直线
C.函数的图象的对称中心是
D.函数的单调递减区间为
11.为了了解市民对各种垃圾进行分类的情况,加强垃圾分类宣传的针对性,指导市民尽快掌握垃圾分类的方法,某市垃圾处理厂连续8周对有害垃圾错误分类情况进行了调查.经整理绘制了如图所示的有害垃圾错误分类重量累积统计图,图中横轴表示时间(单位:周),纵轴表示有害垃圾错误分类的累积重量(单位:吨).根据统计图分析,下列结论正确的是( )
A.当时有害垃圾错误分类的重量加速增长
B.当时有害垃圾错误分类的重量匀速增长
C.当时有害垃圾错误分类的重量相对于当时增长了30%
D.当时有害垃圾错误分类的重量相对于当时减少了1.8吨
12.如图,点是正方体中的侧面
上的一个动点,则下列结论正确的是(ABD)
A.点存在无数个位置满足
B.若正方体的棱长为1,三棱锥的体积最大值为
C.在线段上存在点,使异面直线与所成的角是
D.点存在无数个位置满足到直线和直线的距离相等
第二部分非选择题(90分)
三、填空题:本题共4小题,每小题5分,共20分.
13.已知为奇函数,当时,,则曲线在
处的切线方程是.
14.已知,则,.(本题第一空2分,第二空3分)
15.回文联是我国对联中的一种.用回文形式写成的对联,既可顺读,也可倒读,不仅意思不变,而且颇具趣味.相传,清代北京城里有一家饭馆叫“天然居”,曾有一副有名的回文联:“客上天然居,居然天上客;人过大佛寺,寺佛大过人.”在数学中也有这样一类顺读与倒读都是同一个数的自然数,称之为:“回文数”.如44,585, 2662 等,那么用数字1,2,3, 4,5,6可以组成4位“回文数”的个数为_______.
16.已知双曲线,过其右焦点作渐近线的垂线,垂足为,交轴于点,交另一条渐近线于点,并且点位于点,之间.已知为原点,且,则双曲线的离心率为_________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
在①,②,③这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求出的面积;若问题中的三角形不存在,说明理由.
问题:是否存在三角形,它的内角、、的对边分别为、、,且,
,.
注:如果选择多个条件分别解答,按第一个解答计分.
18.(本小题满分12分)
已知递增等差数列满足,,数列满足.
(1)求的前n项和;
(2)若,求数列的通项公式.
19.(本小题满分12分)
如图,已知圆O的直径AB长为2,上半圆圆弧上有一点C,∠COB=60°,点P是弧AC上的动点,点D是下半圆弧的中点,现以AB为折线,将下半圆所在的平面折成直二面角,连接PO、PD、CD.
(1)当AB//平面PCD时,求PC的长;
(2)当三棱锥P-COD体积最大时,求二
面角D -PC-O的余弦值.
20.(本小题满分12分)
在平面直角坐标系xOy中,已知F(2,0),M(-2,3),动点P满足
(1)求动点P的轨迹C的方程;
(2)过点D(l,0)作直线AB交C于A,B两点,若△AFD的面积是△BFD的面积的2倍,
求︱AB︱.
21.(12分)已知a是常数,函数.
(1)讨论函数在区间上的单调性;
(2)若,证明:.
22.(12分)2019年3月5日,国务院总理李克强作出的政府工作报告中,提到要“惩戒学术不端,力戒学术不端,力戒浮躁之风”,教育部2014年印发的《学术论文抽检办法》通知中规定:每篇抽检的学术论文送3位同行专家进行评议,3位专家中有2位以上(含3位)专家评议意见为“不合格”的学术论文,将认定对“存在问题学术论文”.有且只有l位专家评议意见为“不合格”的学术论文,将再送另外2位同行专家(不同于前3位专家)进行复评,2位复评专家中有l位以上(含l位)专家评议意见为“不合格”的学术论文,将认定为“存在问题学术论文”.设每篇学术论文被每位专家评议为“不合格”的概率均为,且各篇学术论文是否被评议为“不合格”相互独立.
(1)若,求抽检一篇学术论文,被认定为“存在问题学术论文”的概率;
(2)现拟定每篇抽检论文不需要复评的评审费用为900元,需要复评的总评审费用I500元;若某次评审抽检论文总数为 3000篇,求该次评审费用期望的最大值及对应P的值.
平远县高级中学校2021届高三上学期第五次月考
数学参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A D D B A C D C BC AD ABD ABD
二、填空题
13. 14.3, 15.36 16.
解析:
1.A【解析】由题意的①或②,由②得,当时,,不符合,舍去;当时,符合题意.由①得舍去.
2.D【详解】,对应点为,在第四象限.
3.D【详解】因为向量,,所以,
因为,所以,解得,所以.
4.B【解析】对于选项A:若命题p为真命题,命题q为假命题,则命题“”为假命题.
对于选项B:命题“若”的否定是“真命题.
对于选项C:“”是“”的必要不充分条件,假命题.
对于选项D:命题“若则”的否命题为“若则”假命题.
5.A【解析】则的大小关系是
6.C【解析】因为,所以为偶函数,排除D;
因为,所以排除B;因为,
而,所以排除A,故选C.
8.C【详解】可知在单调递增,在单调递增,且,,画出函数图象,
观察图象可知,要使在上的最大值为4,需满足.
9.BC【解析】令,得,解得,即
所以该展开式中二项式系数最大的项是第5项或第6项.故选BC.
10.AD【详解】由图可知:,,即,解得,又当时,.解得,所以,将函数的图象向右平移个单位长度得到函数,则函数是奇函数,对称轴是直线,对称中心是,单调递减区间为.
11.ABD【详解】本题考查统计图的应用,由统计图可知,第2周增长数量比第1周增长数量明显要多,所是加速增长,所以选项A正确;
当时图象是线段,所以是匀速增长,所以选项B正确;
当时增长数量比当时增长数量要少,所以是减少,所以选项C错误;
当时共增长2.4吨,当时共增长0.6吨,所以减少了1.8吨,所以选项D正确.
12.ABD【解析】A.连接,,,,
由正方体的性质可得,,,
则面,当点上时,有,
故点M存在无数个位置满足,故A正确;
B.由己知,
当点M与点重合时,点M到面的距离最大,
则三棱锥的体积最大值为,故B正确;
C.连接,因为,则为异面直线与所成的角
设正方体棱长为1,,则,
点到线的距离为,
,解得,
所以在线段上不存在点M,使异面直线与所成的角是30°,故C错误;
D.连接,过M作,交AD于N,由面,面,得,则为点M到直线的距离,为点到直线AD的距离,由己知,则点M在以为焦点,以AD为准线的抛物线上,故这样的点M有无数个,故D正确.
13.【详解】为奇函数,当时,,
可得,,,
根据奇函数性质可得:
,可得
故:
∴曲线在处的切线方程是:整理可得:
14.3,【解析】因为,所以,解得,所以.
17、解:解法一:由
结合正弦定理可得:………………………………1分
因为,所以……………………………………………2分
因为
所以…………………………………………3分
因为,所以……………………………………………4分
因为,所以,所以……………………………5分
由余弦定理得,所以……………6分
选择条件①的解析:根据,结合正弦定理得…………7分
联立方程组,解得:……………………………8分
所以的面积………………………………………10分
选择条件②的解析:
联立方程组,化简得:…………………………7分
解得 ………………………………………………8分
(注:没有解出a,b,则需说明存在,否则扣1分)
所以的面积 ……………………………10分
选择条件③的解析:由得…………9分
与矛盾,所以问题中的三角形不存在 ……………………………10分
18、解:(1)设数列公差为,由,………2分
解得:或(舍去),所以,,……5分
………………6分
(2),
…………………12分
19.解:(1)∵AB//平面PCD,AB平面OCP,平面OCP∩平面PCD= PC,
∴由线面平行的性质定理得AB // PC.…………………2分
又∠COB=60°,可得∠OCP=60°,而
OC= OP,△OCP为正角形,所以PC=1.……5分
(2) ∵二面角为直二面角,DO⊥AB,
所以DO⊥平面COP,而VP- COD= VD- COP,
∴当CO⊥OP时,三棱锥P-COD体积最大.……7分
因为OP,OD,OC两两垂直,
所以OP,OD,OC分别为x,y,z轴建空间直角坐标系,……8分
P(1,0,0),D(0,1,0),C(0,0,1),=(-1,0,1),=(1,-1,0)
令平面DPC的法向量为
,取(1,1,1)……10分
又取平面PCO的法向量为(0,1,0)
设二面角D-PC-O的平面角为a,,
故二面角D-PC-O的余弦值为.……12分
20.解:(1)设,则,由得.化简得即动点P的轨迹C的方程为(4分)
21.解:(1),………1分
①当时,,,
所以在(0,1)上递减,在递增.…………2分
②当时,,或,
所以在上递减,在,上递增.…………3分
③当时,,在区间上递增,……………4分
④当时,,或,
所以在上递减,在(0,1),上递增.…………5分
综上所述,①当时,在(0,1)上递减,在递增.
②当时,在上递减,在,上递增,
③当时,在区间上递增.
④当时,在上递减,在(0,1),上递增.………6分
(2)要证,只需证…………7分
,故只需证,即证,………8分
令,则,………10分
故在(0,1)上递增,所以,故.……12分
22.解:(1)因为一篇学术论文初评被认定为“存在问题学术论文”的概率为
,…………1分
一篇学术论文复评被认定为“存在问题学术论文”的概率为
,…………2分
所以一篇学术论文被认定为“存在问题学术论文”的概率为
…………4分
时,
所以抽检一篇的学术论文被认定为“存在问题学术论文”的概率为.………5分
(2)设每篇学术论文的评审费为X元,则X的可能取值为900,1500.………6分
,,……… 7分
.…8分
令,,
.…………9分
当时,,在上单调递增;
当时,,在上单调递减.…………10分
所以的最大值为. ……………11分
所以最高费用为(万元).对应.…12分
平远县高级中学校2021届高三上学期第五次月考
数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。考试时间120分钟,满分150分。考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效。交卷时只交答题卡。
第一部分选择题(共60分)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.
1.已知集合,若,则()
A.-1 B.0 C.1 D.2
2.在复平面内,复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.己知向量,,著,则( )
A.10 B.2 C. D.
4.下列判断正确的是( )
A.若命题为真命题,命题为假命题,则命题“”为真命题
B.命题“”的否定是“”
C.“”是“”的充分不必要条件
D.命题“若,则”的否命题为“若,则”
5.已知,则的大小关系是( )
A. B. C. D.
6.函数的大致图象为( )
7.如图,、分别是正方形的边、的中点,把,,折起构成一个三棱锥(,,重合于点),则三棱锥的外接球与内切球的半径之比是()
A. B. C. D.
8.若函数在上的最大值为4,则a的取值范围为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目要求,全选对的得5分,有选错的得0分,部分选对的得3分.
9.已知的展开式中各项的系数之和为-512,则该展开式中二项式系数最大的项可以是( )
A.第4项 B.第5项 C.第6项 D.第7项
10.如图是函数的部分图象,将函数的图象向右平移个单位长度得到函数的图象,则下列命题正确的是( )
A.是奇函数
B.函数的图象的对称轴是直线
C.函数的图象的对称中心是
D.函数的单调递减区间为
11.为了了解市民对各种垃圾进行分类的情况,加强垃圾分类宣传的针对性,指导市民尽快掌握垃圾分类的方法,某市垃圾处理厂连续8周对有害垃圾错误分类情况进行了调查.经整理绘制了如图所示的有害垃圾错误分类重量累积统计图,图中横轴表示时间(单位:周),纵轴表示有害垃圾错误分类的累积重量(单位:吨).根据统计图分析,下列结论正确的是( )
A.当时有害垃圾错误分类的重量加速增长
B.当时有害垃圾错误分类的重量匀速增长
C.当时有害垃圾错误分类的重量相对于当时增长了30%
D.当时有害垃圾错误分类的重量相对于当时减少了1.8吨
12.如图,点是正方体中的侧面
上的一个动点,则下列结论正确的是(ABD)
A.点存在无数个位置满足
B.若正方体的棱长为1,三棱锥的体积最大值为
C.在线段上存在点,使异面直线与所成的角是
D.点存在无数个位置满足到直线和直线的距离相等
第二部分非选择题(90分)
三、填空题:本题共4小题,每小题5分,共20分.
13.已知为奇函数,当时,,则曲线在
处的切线方程是.
14.已知,则,.(本题第一空2分,第二空3分)
15.回文联是我国对联中的一种.用回文形式写成的对联,既可顺读,也可倒读,不仅意思不变,而且颇具趣味.相传,清代北京城里有一家饭馆叫“天然居”,曾有一副有名的回文联:“客上天然居,居然天上客;人过大佛寺,寺佛大过人.”在数学中也有这样一类顺读与倒读都是同一个数的自然数,称之为:“回文数”.如44,585, 2662 等,那么用数字1,2,3, 4,5,6可以组成4位“回文数”的个数为_______.
16.已知双曲线,过其右焦点作渐近线的垂线,垂足为,交轴于点,交另一条渐近线于点,并且点位于点,之间.已知为原点,且,则双曲线的离心率为_________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
在①,②,③这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求出的面积;若问题中的三角形不存在,说明理由.
问题:是否存在三角形,它的内角、、的对边分别为、、,且,
,.
注:如果选择多个条件分别解答,按第一个解答计分.
18.(本小题满分12分)
已知递增等差数列满足,,数列满足.
(1)求的前n项和;
(2)若,求数列的通项公式.
19.(本小题满分12分)
如图,已知圆O的直径AB长为2,上半圆圆弧上有一点C,∠COB=60°,点P是弧AC上的动点,点D是下半圆弧的中点,现以AB为折线,将下半圆所在的平面折成直二面角,连接PO、PD、CD.
(1)当AB//平面PCD时,求PC的长;
(2)当三棱锥P-COD体积最大时,求二
面角D -PC-O的余弦值.
20.(本小题满分12分)
在平面直角坐标系xOy中,已知F(2,0),M(-2,3),动点P满足
(1)求动点P的轨迹C的方程;
(2)过点D(l,0)作直线AB交C于A,B两点,若△AFD的面积是△BFD的面积的2倍,
求︱AB︱.
21.(12分)已知a是常数,函数.
(1)讨论函数在区间上的单调性;
(2)若,证明:.
22.(12分)2019年3月5日,国务院总理李克强作出的政府工作报告中,提到要“惩戒学术不端,力戒学术不端,力戒浮躁之风”,教育部2014年印发的《学术论文抽检办法》通知中规定:每篇抽检的学术论文送3位同行专家进行评议,3位专家中有2位以上(含3位)专家评议意见为“不合格”的学术论文,将认定对“存在问题学术论文”.有且只有l位专家评议意见为“不合格”的学术论文,将再送另外2位同行专家(不同于前3位专家)进行复评,2位复评专家中有l位以上(含l位)专家评议意见为“不合格”的学术论文,将认定为“存在问题学术论文”.设每篇学术论文被每位专家评议为“不合格”的概率均为,且各篇学术论文是否被评议为“不合格”相互独立.
(1)若,求抽检一篇学术论文,被认定为“存在问题学术论文”的概率;
(2)现拟定每篇抽检论文不需要复评的评审费用为900元,需要复评的总评审费用I500元;若某次评审抽检论文总数为 3000篇,求该次评审费用期望的最大值及对应P的值.
平远县高级中学校2021届高三上学期第五次月考
数学参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A D D B A C D C BC AD ABD ABD
二、填空题
13. 14.3, 15.36 16.
解析:
1.A【解析】由题意的①或②,由②得,当时,,不符合,舍去;当时,符合题意.由①得舍去.
2.D【详解】,对应点为,在第四象限.
3.D【详解】因为向量,,所以,
因为,所以,解得,所以.
4.B【解析】对于选项A:若命题p为真命题,命题q为假命题,则命题“”为假命题.
对于选项B:命题“若”的否定是“真命题.
对于选项C:“”是“”的必要不充分条件,假命题.
对于选项D:命题“若则”的否命题为“若则”假命题.
5.A【解析】则的大小关系是
6.C【解析】因为,所以为偶函数,排除D;
因为,所以排除B;因为,
而,所以排除A,故选C.
8.C【详解】可知在单调递增,在单调递增,且,,画出函数图象,
观察图象可知,要使在上的最大值为4,需满足.
9.BC【解析】令,得,解得,即
所以该展开式中二项式系数最大的项是第5项或第6项.故选BC.
10.AD【详解】由图可知:,,即,解得,又当时,.解得,所以,将函数的图象向右平移个单位长度得到函数,则函数是奇函数,对称轴是直线,对称中心是,单调递减区间为.
11.ABD【详解】本题考查统计图的应用,由统计图可知,第2周增长数量比第1周增长数量明显要多,所是加速增长,所以选项A正确;
当时图象是线段,所以是匀速增长,所以选项B正确;
当时增长数量比当时增长数量要少,所以是减少,所以选项C错误;
当时共增长2.4吨,当时共增长0.6吨,所以减少了1.8吨,所以选项D正确.
12.ABD【解析】A.连接,,,,
由正方体的性质可得,,,
则面,当点上时,有,
故点M存在无数个位置满足,故A正确;
B.由己知,
当点M与点重合时,点M到面的距离最大,
则三棱锥的体积最大值为,故B正确;
C.连接,因为,则为异面直线与所成的角
设正方体棱长为1,,则,
点到线的距离为,
,解得,
所以在线段上不存在点M,使异面直线与所成的角是30°,故C错误;
D.连接,过M作,交AD于N,由面,面,得,则为点M到直线的距离,为点到直线AD的距离,由己知,则点M在以为焦点,以AD为准线的抛物线上,故这样的点M有无数个,故D正确.
13.【详解】为奇函数,当时,,
可得,,,
根据奇函数性质可得:
,可得
故:
∴曲线在处的切线方程是:整理可得:
14.3,【解析】因为,所以,解得,所以.
17、解:解法一:由
结合正弦定理可得:………………………………1分
因为,所以……………………………………………2分
因为
所以…………………………………………3分
因为,所以……………………………………………4分
因为,所以,所以……………………………5分
由余弦定理得,所以……………6分
选择条件①的解析:根据,结合正弦定理得…………7分
联立方程组,解得:……………………………8分
所以的面积………………………………………10分
选择条件②的解析:
联立方程组,化简得:…………………………7分
解得 ………………………………………………8分
(注:没有解出a,b,则需说明存在,否则扣1分)
所以的面积 ……………………………10分
选择条件③的解析:由得…………9分
与矛盾,所以问题中的三角形不存在 ……………………………10分
18、解:(1)设数列公差为,由,………2分
解得:或(舍去),所以,,……5分
………………6分
(2),
…………………12分
19.解:(1)∵AB//平面PCD,AB平面OCP,平面OCP∩平面PCD= PC,
∴由线面平行的性质定理得AB // PC.…………………2分
又∠COB=60°,可得∠OCP=60°,而
OC= OP,△OCP为正角形,所以PC=1.……5分
(2) ∵二面角为直二面角,DO⊥AB,
所以DO⊥平面COP,而VP- COD= VD- COP,
∴当CO⊥OP时,三棱锥P-COD体积最大.……7分
因为OP,OD,OC两两垂直,
所以OP,OD,OC分别为x,y,z轴建空间直角坐标系,……8分
P(1,0,0),D(0,1,0),C(0,0,1),=(-1,0,1),=(1,-1,0)
令平面DPC的法向量为
,取(1,1,1)……10分
又取平面PCO的法向量为(0,1,0)
设二面角D-PC-O的平面角为a,,
故二面角D-PC-O的余弦值为.……12分
20.解:(1)设,则,由得.化简得即动点P的轨迹C的方程为(4分)
21.解:(1),………1分
①当时,,,
所以在(0,1)上递减,在递增.…………2分
②当时,,或,
所以在上递减,在,上递增.…………3分
③当时,,在区间上递增,……………4分
④当时,,或,
所以在上递减,在(0,1),上递增.…………5分
综上所述,①当时,在(0,1)上递减,在递增.
②当时,在上递减,在,上递增,
③当时,在区间上递增.
④当时,在上递减,在(0,1),上递增.………6分
(2)要证,只需证…………7分
,故只需证,即证,………8分
令,则,………10分
故在(0,1)上递增,所以,故.……12分
22.解:(1)因为一篇学术论文初评被认定为“存在问题学术论文”的概率为
,…………1分
一篇学术论文复评被认定为“存在问题学术论文”的概率为
,…………2分
所以一篇学术论文被认定为“存在问题学术论文”的概率为
…………4分
时,
所以抽检一篇的学术论文被认定为“存在问题学术论文”的概率为.………5分
(2)设每篇学术论文的评审费为X元,则X的可能取值为900,1500.………6分
,,……… 7分
.…8分
令,,
.…………9分
当时,,在上单调递增;
当时,,在上单调递减.…………10分
所以的最大值为. ……………11分
所以最高费用为(万元).对应.…12分
同课章节目录
