北师大版八年级数学下册课时达标训练:6.2.1利用边判定平行四边形(Word版含答案)
文档属性
| 名称 | 北师大版八年级数学下册课时达标训练:6.2.1利用边判定平行四边形(Word版含答案) | 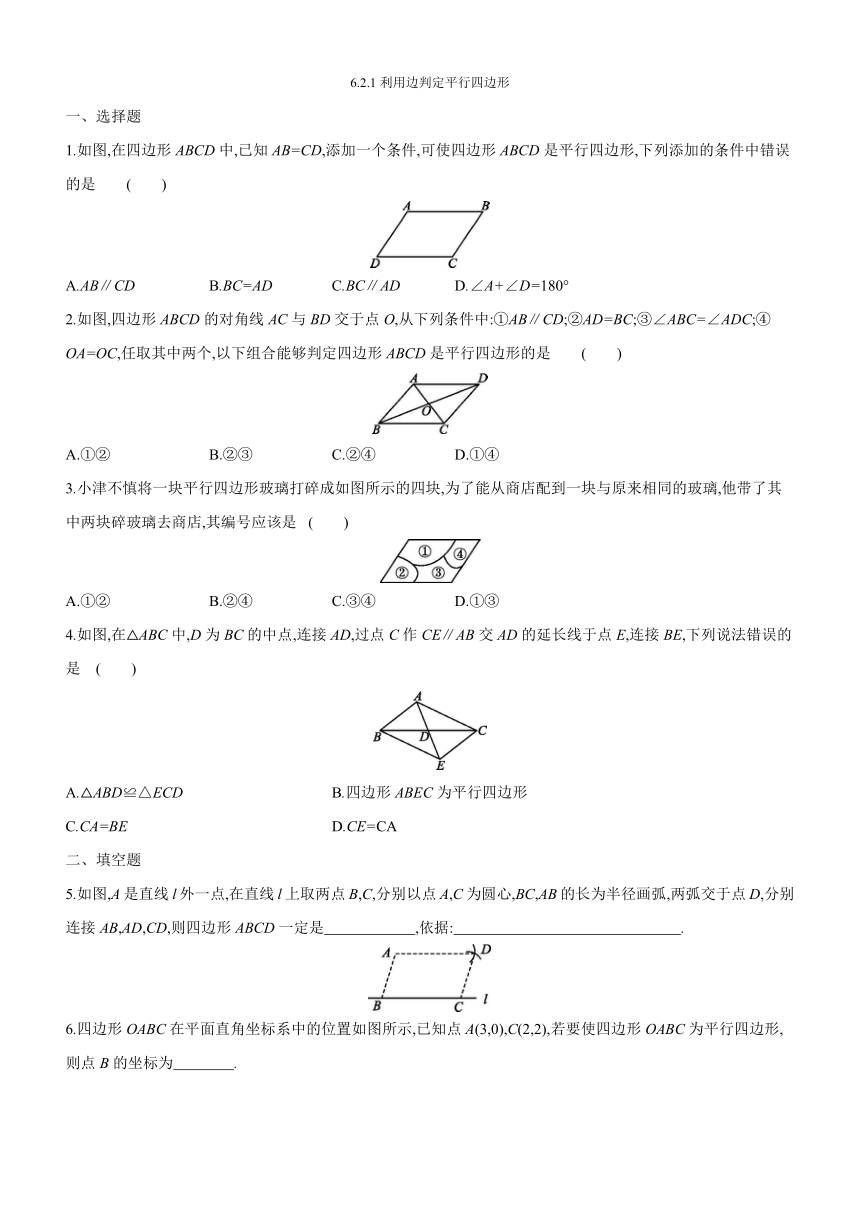 | |
| 格式 | zip | ||
| 文件大小 | 139.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 19:56:34 | ||
图片预览



文档简介
6.2.1利用边判定平行四边形
一、选择题
1.如图,在四边形ABCD中,已知AB=CD,添加一个条件,可使四边形ABCD是平行四边形,下列添加的条件中错误的是
( )
A.AB∥CD
B.BC=AD
C.BC∥AD
D.∠A+∠D=180°
2.如图,四边形ABCD的对角线AC与BD交于点O,从下列条件中:①AB∥CD;②AD=BC;③∠ABC=∠ADC;④OA=OC,任取其中两个,以下组合能够判定四边形ABCD是平行四边形的是
( )
A.①②
B.②③
C.②④
D.①④
3.小津不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能从商店配到一块与原来相同的玻璃,他带了其中两块碎玻璃去商店,其编号应该是
( )
A.①②
B.②④
C.③④
D.①③
4.如图,在△ABC中,D为BC的中点,连接AD,过点C作CE∥AB交AD的延长线于点E,连接BE,下列说法错误的是
( )
A.△ABD≌△ECD
B.四边形ABEC为平行四边形
C.CA=BE
D.CE=CA
二、填空题
5.如图,A是直线l外一点,在直线l上取两点B,C,分别以点A,C为圆心,BC,AB的长为半径画弧,两弧交于点D,分别连接AB,AD,CD,则四边形ABCD一定是 ,依据: .
6.四边形OABC在平面直角坐标系中的位置如图所示,已知点A(3,0),C(2,2),若要使四边形OABC为平行四边形,则点B的坐标为 .?
7.如图,已知AB=CD,AD=BC,E,F是DB上的两点,且AE∥CF.若∠AEB=115°,
∠ADB=35°,则∠BCF= °.?
8.如图,在四边形ABCD中,AD∥BC且AD=9
cm,BC=6
cm,点P,Q分别从点A,C同时出发,点P以1
cm/s的速度由点A向点D运动,点Q以2
cm/s的速度由点C向点B运动.当其中一点到达终点时,另一点也随之停止运动,则经过 s后直线PQ将四边形ABCD截出一个平行四边形.?
三、解答题
9.如图,在四边形ABCD中,AD∥BC,延长BC到点E,使CE=BC,连接AE交CD于点F,F是CD的中点.
求证:(1)△ADF≌△ECF;
(2)四边形ABCD是平行四边形.
10.如图,已知△ABC是等边三角形,E为AC上一点,连接BE.将AC绕点E旋转,使点C落在BC上的点D处,点A落在BC上方的点F处,连接AF.求证:四边形ABDF是平行四边形.
11.如图,AB=CD,E,F分别为AB,CD上的点,连接BC,分别与AF,ED相交于点G,H,∠B=∠C,BH=CG.求证:四边形AFDE是平行四边形.
12.如图所示,在?ABCD中,如果M,N,P,Q分别为AB,BC,CD,DA上的点,且AM=BN=CP=DQ,那么四边形MNPQ是平行四边形吗?试说明理由.
13.如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位长度的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位长度的速度运动,在线段QC上取点E,使得QE=2,连接PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长.
(2)是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,请求出t的值;若不存在,请说明理由.
答案
1.[答案]
C
2.[答案]
D
3.解析:
D 只有①③两块角的两边互相平行,且中间部分相连,角的两边的延长线的交点就是平行四边形的顶点,
∴带①③两块碎玻璃,就可以确定平行四边形的大小.故选D.
4.[答案]
D
5.[答案]
平行四边形 两组对边分别相等的四边形是平行四边形
6.[答案]
(5,2)
解析:
∵四边形OABC是平行四边形,
∴OA=BC,OA∥BC.
∵A(3,0),C(2,2),
∴BC=OA=3,∴B(5,2).
故答案为(5,2).
7.[答案]
80
解析:
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AD∥BC,∴∠CBF=∠ADE.
∵AE∥CF,∴∠CFB=∠AED.
又∵BC=DA,∴△BCF≌△DAE,
∴∠BCF=∠DAE.
∵∠AEB=115°,∠ADB=35°,∠AEB=∠DAE+∠ADB,
∴∠DAE=∠AEB-∠ADB=115°-35°=80°,
∴∠BCF=80°.
8.[答案]
2或3
解析:
设点P,Q运动的时间为t
s.依题意得CQ=2t
cm,BQ=(6-2t)cm,AP=t
cm,PD=(9-t)cm.
①当BQ=AP时,四边形APQB是平行四边形,则6-2t=t,
解得t=2;
②当CQ=PD时,四边形CQPD是平行四边形,则2t=9-t,
解得t=3.
所以经过2
s或3
s后,直线PQ将四边形ABCD截出一个平行四边形.
9.证明:(1)∵AD∥BC,∴∠DAF=∠E.
∵F是CD的中点,∴DF=CF.
又∵∠AFD=∠EFC,
∴△ADF≌△ECF(AAS).
(2)∵△ADF≌△ECF,∴AD=EC.
∵CE=BC,∴AD=BC.
又∵AD∥BC,∴四边形ABCD是平行四边形.
10.证明:∵△ABC是等边三角形,
∴AC=AB,∠ACB=∠ABC=60°.
∵将AC绕点E旋转,点C落在BC上的点D处,点A落在BC上方的点F处,
∴ED=CE,AC=FD,
∴△EDC是等边三角形,AB=FD,
∴∠EDC=60°,
∴∠EDC=∠ABC,
∴AB∥FD.
又∵AB=FD,
∴四边形ABDF是平行四边形.
11.证明:∵BH=CG,
∴BH+HG=CG+HG,即BG=CH.
又∵∠B=∠C,AB=DC,
∴△ABG≌△DCH(SAS),
∴∠AGB=∠DHC,∴AF∥DE.
∵∠B=∠C,∴AB∥CD,
∴四边形AFDE是平行四边形.
12.解:四边形MNPQ是平行四边形.
理由:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠A=∠C,∠B=∠D.
∵AM=BN=CP=DQ,
∴AQ=CN,BM=DP,
∴△AMQ≌△CPN,△BMN≌△DPQ,
∴MQ=PN,MN=PQ,
∴四边形MNPQ是平行四边形.
13.解:(1)过点A作AM⊥BC于点M,设PE交AC于点N.
∵∠BAC=90°,∠B=45°,
∴∠C=45°=∠B,∴AB=AC,
∴∠BAM=∠CAM=45°,
∴BM=CM=AM=BC=5.
∵AD∥BC,
∴∠PAN=∠C=45°.
∵PE⊥BC,
∴PE=AM=5,PE⊥AD,
∴△APN和△CEN都是等腰直角三角形,
∴PN=AP=t,CE=NE=5-t.
∵CE=CQ-QE=2t-2,
∴5-t=2t-2,
解得t=,
∴BQ=BC-CQ=10-2×=.
(2)存在.
若以A,B,E,P为顶点的四边形为平行四边形,则AP=BE,
∴t=10-2t+2或t=2t-2-10,
解得t=4或t=12.
∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t的值为4或12.
一、选择题
1.如图,在四边形ABCD中,已知AB=CD,添加一个条件,可使四边形ABCD是平行四边形,下列添加的条件中错误的是
( )
A.AB∥CD
B.BC=AD
C.BC∥AD
D.∠A+∠D=180°
2.如图,四边形ABCD的对角线AC与BD交于点O,从下列条件中:①AB∥CD;②AD=BC;③∠ABC=∠ADC;④OA=OC,任取其中两个,以下组合能够判定四边形ABCD是平行四边形的是
( )
A.①②
B.②③
C.②④
D.①④
3.小津不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能从商店配到一块与原来相同的玻璃,他带了其中两块碎玻璃去商店,其编号应该是
( )
A.①②
B.②④
C.③④
D.①③
4.如图,在△ABC中,D为BC的中点,连接AD,过点C作CE∥AB交AD的延长线于点E,连接BE,下列说法错误的是
( )
A.△ABD≌△ECD
B.四边形ABEC为平行四边形
C.CA=BE
D.CE=CA
二、填空题
5.如图,A是直线l外一点,在直线l上取两点B,C,分别以点A,C为圆心,BC,AB的长为半径画弧,两弧交于点D,分别连接AB,AD,CD,则四边形ABCD一定是 ,依据: .
6.四边形OABC在平面直角坐标系中的位置如图所示,已知点A(3,0),C(2,2),若要使四边形OABC为平行四边形,则点B的坐标为 .?
7.如图,已知AB=CD,AD=BC,E,F是DB上的两点,且AE∥CF.若∠AEB=115°,
∠ADB=35°,则∠BCF= °.?
8.如图,在四边形ABCD中,AD∥BC且AD=9
cm,BC=6
cm,点P,Q分别从点A,C同时出发,点P以1
cm/s的速度由点A向点D运动,点Q以2
cm/s的速度由点C向点B运动.当其中一点到达终点时,另一点也随之停止运动,则经过 s后直线PQ将四边形ABCD截出一个平行四边形.?
三、解答题
9.如图,在四边形ABCD中,AD∥BC,延长BC到点E,使CE=BC,连接AE交CD于点F,F是CD的中点.
求证:(1)△ADF≌△ECF;
(2)四边形ABCD是平行四边形.
10.如图,已知△ABC是等边三角形,E为AC上一点,连接BE.将AC绕点E旋转,使点C落在BC上的点D处,点A落在BC上方的点F处,连接AF.求证:四边形ABDF是平行四边形.
11.如图,AB=CD,E,F分别为AB,CD上的点,连接BC,分别与AF,ED相交于点G,H,∠B=∠C,BH=CG.求证:四边形AFDE是平行四边形.
12.如图所示,在?ABCD中,如果M,N,P,Q分别为AB,BC,CD,DA上的点,且AM=BN=CP=DQ,那么四边形MNPQ是平行四边形吗?试说明理由.
13.如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位长度的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位长度的速度运动,在线段QC上取点E,使得QE=2,连接PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长.
(2)是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,请求出t的值;若不存在,请说明理由.
答案
1.[答案]
C
2.[答案]
D
3.解析:
D 只有①③两块角的两边互相平行,且中间部分相连,角的两边的延长线的交点就是平行四边形的顶点,
∴带①③两块碎玻璃,就可以确定平行四边形的大小.故选D.
4.[答案]
D
5.[答案]
平行四边形 两组对边分别相等的四边形是平行四边形
6.[答案]
(5,2)
解析:
∵四边形OABC是平行四边形,
∴OA=BC,OA∥BC.
∵A(3,0),C(2,2),
∴BC=OA=3,∴B(5,2).
故答案为(5,2).
7.[答案]
80
解析:
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AD∥BC,∴∠CBF=∠ADE.
∵AE∥CF,∴∠CFB=∠AED.
又∵BC=DA,∴△BCF≌△DAE,
∴∠BCF=∠DAE.
∵∠AEB=115°,∠ADB=35°,∠AEB=∠DAE+∠ADB,
∴∠DAE=∠AEB-∠ADB=115°-35°=80°,
∴∠BCF=80°.
8.[答案]
2或3
解析:
设点P,Q运动的时间为t
s.依题意得CQ=2t
cm,BQ=(6-2t)cm,AP=t
cm,PD=(9-t)cm.
①当BQ=AP时,四边形APQB是平行四边形,则6-2t=t,
解得t=2;
②当CQ=PD时,四边形CQPD是平行四边形,则2t=9-t,
解得t=3.
所以经过2
s或3
s后,直线PQ将四边形ABCD截出一个平行四边形.
9.证明:(1)∵AD∥BC,∴∠DAF=∠E.
∵F是CD的中点,∴DF=CF.
又∵∠AFD=∠EFC,
∴△ADF≌△ECF(AAS).
(2)∵△ADF≌△ECF,∴AD=EC.
∵CE=BC,∴AD=BC.
又∵AD∥BC,∴四边形ABCD是平行四边形.
10.证明:∵△ABC是等边三角形,
∴AC=AB,∠ACB=∠ABC=60°.
∵将AC绕点E旋转,点C落在BC上的点D处,点A落在BC上方的点F处,
∴ED=CE,AC=FD,
∴△EDC是等边三角形,AB=FD,
∴∠EDC=60°,
∴∠EDC=∠ABC,
∴AB∥FD.
又∵AB=FD,
∴四边形ABDF是平行四边形.
11.证明:∵BH=CG,
∴BH+HG=CG+HG,即BG=CH.
又∵∠B=∠C,AB=DC,
∴△ABG≌△DCH(SAS),
∴∠AGB=∠DHC,∴AF∥DE.
∵∠B=∠C,∴AB∥CD,
∴四边形AFDE是平行四边形.
12.解:四边形MNPQ是平行四边形.
理由:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠A=∠C,∠B=∠D.
∵AM=BN=CP=DQ,
∴AQ=CN,BM=DP,
∴△AMQ≌△CPN,△BMN≌△DPQ,
∴MQ=PN,MN=PQ,
∴四边形MNPQ是平行四边形.
13.解:(1)过点A作AM⊥BC于点M,设PE交AC于点N.
∵∠BAC=90°,∠B=45°,
∴∠C=45°=∠B,∴AB=AC,
∴∠BAM=∠CAM=45°,
∴BM=CM=AM=BC=5.
∵AD∥BC,
∴∠PAN=∠C=45°.
∵PE⊥BC,
∴PE=AM=5,PE⊥AD,
∴△APN和△CEN都是等腰直角三角形,
∴PN=AP=t,CE=NE=5-t.
∵CE=CQ-QE=2t-2,
∴5-t=2t-2,
解得t=,
∴BQ=BC-CQ=10-2×=.
(2)存在.
若以A,B,E,P为顶点的四边形为平行四边形,则AP=BE,
∴t=10-2t+2或t=2t-2-10,
解得t=4或t=12.
∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t的值为4或12.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
