北师大版八年级数学下册课时达标训练:1.4.1角平分线(Word版含解析)
文档属性
| 名称 | 北师大版八年级数学下册课时达标训练:1.4.1角平分线(Word版含解析) | 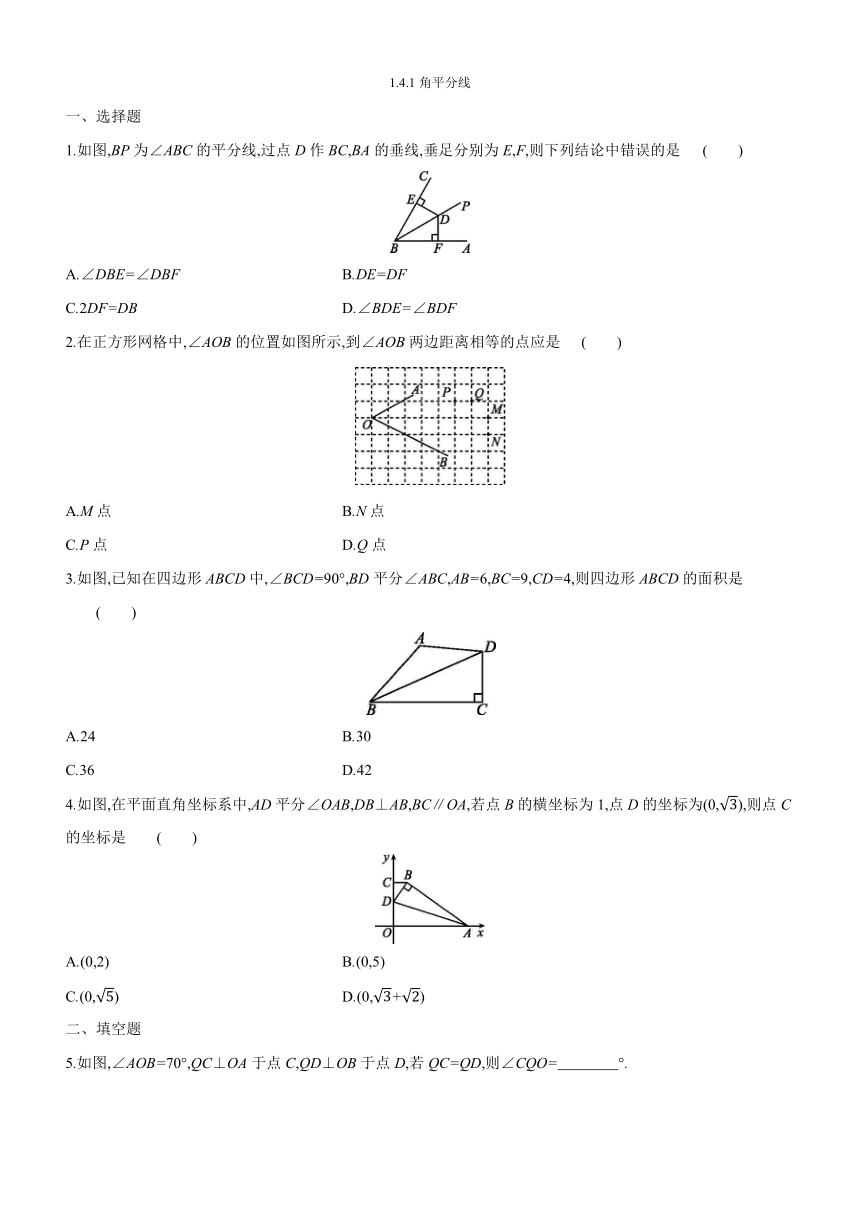 | |
| 格式 | zip | ||
| 文件大小 | 244.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 20:03:35 | ||
图片预览




文档简介
1.4.1角平分线
一、选择题
1.如图,BP为∠ABC的平分线,过点D作BC,BA的垂线,垂足分别为E,F,则下列结论中错误的是
( )
A.∠DBE=∠DBF
B.DE=DF
C.2DF=DB
D.∠BDE=∠BDF
2.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是
( )
A.M点
B.N点
C.P点
D.Q点
3.如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是
( )
A.24
B.30
C.36
D.42
4.如图,在平面直角坐标系中,AD平分∠OAB,DB⊥AB,BC∥OA,若点B的横坐标为1,点D的坐标为(0,),则点C的坐标是
( )
A.(0,2)
B.(0,5)
C.(0,)
D.(0,+)
二、填空题
5.如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠CQO= °.?
6.已知:如图,AB∥CD,AP,CP分别平分∠BAC和∠ACD,PE⊥AC于点E,且PE=3
cm,则AB与CD之间的距离为 cm.?
7.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB.若EC=1,则EF= .?
8.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为48和26,则△EDF的面积为 .?
三、解答题
9.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,CD=3.
(1)求DE的长;
(2)若AC=6,BC=8,求△ADB的面积.
10.已知:如图,P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,F,G分别是OA,OB上的点,且PF=PG,DF=EG.
求证:OC是∠AOB的平分线.
11.如图,某地有两个村庄M,N,和两条相交叉的公路OA,OB,现计划在∠AOB内部修建一个物资仓库,希望仓库到两个村庄的距离相等,到两条公路的距离也相等,请你确定该仓库的位置.
12.如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O,E,F分别在BD,BC,AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
13.感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图③,在四边形ABDC中,∠B=45°,∠C=135°,DB=DC=a,则AB-AC= (用含a的代数式表示)?
答案
1.[答案]
C
2.解析:
A 从图上可以看出点M在∠AOB的平分线上,其他三点均不在∠AOB的平分线上,
所以点M到∠AOB两边的距离相等.故选A.
3.解析:
B 如图,过点D作DH⊥BA交BA的延长线于点H.∵BD平分∠ABC,∠BCD=90°,∴DH=CD=4,∴四边形ABCD的面积=S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.故选B.
4.解析:
D ∵AD平分∠OAB,DB⊥AB,DO⊥OA,∴DB=DO=.
∵点B的横坐标为1,∴BC=1.∵OA⊥y轴,BC∥OA,∴BC⊥y轴,即∠BCD=90°,
∴CD==,
∴OC=OD+CD=+,∴点C的坐标是(0,+).故选D.
5.[答案]
55
解析:
∵QC⊥OA于点C,QD⊥OB于点D,QC=QD,∴OQ是∠AOB的平分线.
∵∠AOB=70°,
∴∠AOQ=∠AOB=×70°=35°,
∴∠CQO=90°-∠AOQ=90°-35°=55°.
故答案为55.
6.[答案]
6
解析:
过点P作PM⊥AB于点M,并反向延长交CD于点N.
∵AB∥CD,∴PN⊥CD.∵AP平分∠BAC,PE⊥AC,PM⊥AB,PE=3
cm,∴PM=PE=3
cm.
同理PN=PE=3
cm,∴MN=PM+PN=6
cm,∴AB与CD之间的距离是6
cm.
7.[答案]
2
解析:
如图,过点E作EG⊥OA于点G.根据角平分线的性质定理得到EG的长,再根据平行线的性质得到∠OEF=∠COE=15°,然后利用三角形的外角和内角的关系求出∠EFG=30°,利用在直角三角形中,30°角所对的直角边等于斜边的一半解题.
8.[答案]
11
解析:
如图,过点D作DH⊥AC于点H.
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,∴DF=DH.在Rt△FDE和Rt△HDG中,∵DF=
DH,DE=DG,∴Rt△FDE≌Rt△HDG(HL).同理,Rt△FDA≌Rt△HDA(HL).设△EDF的面积为x,由题意,得48-x=26+x,解得x=11,即△EDF的面积为11.故答案为11.
9.解:(1)∵在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,CD=3,∴DE=CD=3.
(2)∵在Rt△ABC中,∠C=90°,AC=6,BC=8,CD=3,∴BD=BC-CD=5,
∴S△ADB=BD·AC=×5×6=15.
10.证明:∵PD⊥OA于点D,PE⊥OB于点E,
∴∠PDF=∠PEG=90°.
在Rt△PFD和Rt△PGE中,
∵PF=PG,DF=EG,
∴Rt△PFD≌Rt△PGE(HL),
∴PD=PE.
∵P是OC上一点,PD⊥OA,PE⊥OB,
∴OC是∠AOB的平分线.
11.解:如图,点P即为该仓库的位置.
12.解:(1)证明:如图,过点O作OM⊥AB于点M.
∵四边形OECF是正方形,
∴OE=EC=CF=OF,OE⊥BC,OF⊥AC.
∵BD平分∠ABC,
∴OM=OE,
∴OM=OF.
又∵OM⊥AB,OF⊥AC,
∴点O在∠BAC的平分线上.
(2)方法一:∵在Rt△ABC中,∠C=90°,AC=5,BC=12,∴由勾股定理得AB=13.
易证BE=BM,AM=AF.
又∵BE=BC-CE,AF=AC-CF,CE=CF=OE,
∴BE=12-OE,AF=5-OE.
∵BM+AM=AB,∴BE+AF=13,
即12-OE+5-OE=13,
解得OE=2,即OE的长为2.
方法二:利用面积法.连接OC.
∵在Rt△ABC中,∠C=90°,AC=5,BC=12,
∴由勾股定理得AB=13.
∵S△ABC=AC·BC,S△ABC=BC·OE+AC·OF+AB·OM,
∴AC·BC=BC·OE+AC·OF+AB·OM,
即×5×12=×12OE+×5OF+×13OM.
由(1)得,OM=OE=OF,
∴OE=2.
13.解:探究:证明:如图①,过点D作DE⊥AB于点E,DF⊥AC,交AC的延长线于点F.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD.
在△DEB和△DFC中,
∵∠DEB=∠F=90°,∠B=∠FCD,DE=DF,
∴△DEB≌△DFC,∴DB=DC.
应用:如图②,连接AD,过点D作DE⊥AB于点E,DF⊥AC,交AC的延长线于点F.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD.
在△DEB和△DFC中,
∵∠DEB=∠F=90°,∠B=∠FCD,DB=DC,
∴△DEB≌△DFC,∴DE=DF,BE=CF.
在Rt△ADF和Rt△ADE中,
∵AD=AD,DF=DE,
∴Rt△ADF≌Rt△ADE,
∴AF=AE,
∴AB-AC=(AE+BE)-(AF-CF)=2BE.
在Rt△DEB中,
∵∠DEB=90°,∠B=∠EDB=45°,BD=a,
∴BE=a,∴AB-AC=a.
故答案为a.
一、选择题
1.如图,BP为∠ABC的平分线,过点D作BC,BA的垂线,垂足分别为E,F,则下列结论中错误的是
( )
A.∠DBE=∠DBF
B.DE=DF
C.2DF=DB
D.∠BDE=∠BDF
2.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是
( )
A.M点
B.N点
C.P点
D.Q点
3.如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是
( )
A.24
B.30
C.36
D.42
4.如图,在平面直角坐标系中,AD平分∠OAB,DB⊥AB,BC∥OA,若点B的横坐标为1,点D的坐标为(0,),则点C的坐标是
( )
A.(0,2)
B.(0,5)
C.(0,)
D.(0,+)
二、填空题
5.如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠CQO= °.?
6.已知:如图,AB∥CD,AP,CP分别平分∠BAC和∠ACD,PE⊥AC于点E,且PE=3
cm,则AB与CD之间的距离为 cm.?
7.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB.若EC=1,则EF= .?
8.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为48和26,则△EDF的面积为 .?
三、解答题
9.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,CD=3.
(1)求DE的长;
(2)若AC=6,BC=8,求△ADB的面积.
10.已知:如图,P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,F,G分别是OA,OB上的点,且PF=PG,DF=EG.
求证:OC是∠AOB的平分线.
11.如图,某地有两个村庄M,N,和两条相交叉的公路OA,OB,现计划在∠AOB内部修建一个物资仓库,希望仓库到两个村庄的距离相等,到两条公路的距离也相等,请你确定该仓库的位置.
12.如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O,E,F分别在BD,BC,AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
13.感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图③,在四边形ABDC中,∠B=45°,∠C=135°,DB=DC=a,则AB-AC= (用含a的代数式表示)?
答案
1.[答案]
C
2.解析:
A 从图上可以看出点M在∠AOB的平分线上,其他三点均不在∠AOB的平分线上,
所以点M到∠AOB两边的距离相等.故选A.
3.解析:
B 如图,过点D作DH⊥BA交BA的延长线于点H.∵BD平分∠ABC,∠BCD=90°,∴DH=CD=4,∴四边形ABCD的面积=S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.故选B.
4.解析:
D ∵AD平分∠OAB,DB⊥AB,DO⊥OA,∴DB=DO=.
∵点B的横坐标为1,∴BC=1.∵OA⊥y轴,BC∥OA,∴BC⊥y轴,即∠BCD=90°,
∴CD==,
∴OC=OD+CD=+,∴点C的坐标是(0,+).故选D.
5.[答案]
55
解析:
∵QC⊥OA于点C,QD⊥OB于点D,QC=QD,∴OQ是∠AOB的平分线.
∵∠AOB=70°,
∴∠AOQ=∠AOB=×70°=35°,
∴∠CQO=90°-∠AOQ=90°-35°=55°.
故答案为55.
6.[答案]
6
解析:
过点P作PM⊥AB于点M,并反向延长交CD于点N.
∵AB∥CD,∴PN⊥CD.∵AP平分∠BAC,PE⊥AC,PM⊥AB,PE=3
cm,∴PM=PE=3
cm.
同理PN=PE=3
cm,∴MN=PM+PN=6
cm,∴AB与CD之间的距离是6
cm.
7.[答案]
2
解析:
如图,过点E作EG⊥OA于点G.根据角平分线的性质定理得到EG的长,再根据平行线的性质得到∠OEF=∠COE=15°,然后利用三角形的外角和内角的关系求出∠EFG=30°,利用在直角三角形中,30°角所对的直角边等于斜边的一半解题.
8.[答案]
11
解析:
如图,过点D作DH⊥AC于点H.
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,∴DF=DH.在Rt△FDE和Rt△HDG中,∵DF=
DH,DE=DG,∴Rt△FDE≌Rt△HDG(HL).同理,Rt△FDA≌Rt△HDA(HL).设△EDF的面积为x,由题意,得48-x=26+x,解得x=11,即△EDF的面积为11.故答案为11.
9.解:(1)∵在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,CD=3,∴DE=CD=3.
(2)∵在Rt△ABC中,∠C=90°,AC=6,BC=8,CD=3,∴BD=BC-CD=5,
∴S△ADB=BD·AC=×5×6=15.
10.证明:∵PD⊥OA于点D,PE⊥OB于点E,
∴∠PDF=∠PEG=90°.
在Rt△PFD和Rt△PGE中,
∵PF=PG,DF=EG,
∴Rt△PFD≌Rt△PGE(HL),
∴PD=PE.
∵P是OC上一点,PD⊥OA,PE⊥OB,
∴OC是∠AOB的平分线.
11.解:如图,点P即为该仓库的位置.
12.解:(1)证明:如图,过点O作OM⊥AB于点M.
∵四边形OECF是正方形,
∴OE=EC=CF=OF,OE⊥BC,OF⊥AC.
∵BD平分∠ABC,
∴OM=OE,
∴OM=OF.
又∵OM⊥AB,OF⊥AC,
∴点O在∠BAC的平分线上.
(2)方法一:∵在Rt△ABC中,∠C=90°,AC=5,BC=12,∴由勾股定理得AB=13.
易证BE=BM,AM=AF.
又∵BE=BC-CE,AF=AC-CF,CE=CF=OE,
∴BE=12-OE,AF=5-OE.
∵BM+AM=AB,∴BE+AF=13,
即12-OE+5-OE=13,
解得OE=2,即OE的长为2.
方法二:利用面积法.连接OC.
∵在Rt△ABC中,∠C=90°,AC=5,BC=12,
∴由勾股定理得AB=13.
∵S△ABC=AC·BC,S△ABC=BC·OE+AC·OF+AB·OM,
∴AC·BC=BC·OE+AC·OF+AB·OM,
即×5×12=×12OE+×5OF+×13OM.
由(1)得,OM=OE=OF,
∴OE=2.
13.解:探究:证明:如图①,过点D作DE⊥AB于点E,DF⊥AC,交AC的延长线于点F.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD.
在△DEB和△DFC中,
∵∠DEB=∠F=90°,∠B=∠FCD,DE=DF,
∴△DEB≌△DFC,∴DB=DC.
应用:如图②,连接AD,过点D作DE⊥AB于点E,DF⊥AC,交AC的延长线于点F.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD.
在△DEB和△DFC中,
∵∠DEB=∠F=90°,∠B=∠FCD,DB=DC,
∴△DEB≌△DFC,∴DE=DF,BE=CF.
在Rt△ADF和Rt△ADE中,
∵AD=AD,DF=DE,
∴Rt△ADF≌Rt△ADE,
∴AF=AE,
∴AB-AC=(AE+BE)-(AF-CF)=2BE.
在Rt△DEB中,
∵∠DEB=90°,∠B=∠EDB=45°,BD=a,
∴BE=a,∴AB-AC=a.
故答案为a.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
