人教版七年级数学下册 5.1.1 相交线 (1)(共23张)
文档属性
| 名称 | 人教版七年级数学下册 5.1.1 相交线 (1)(共23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
5.1
相交线
一、点与直线有哪几种位置关系:
·
·
A
P
m
2
、点
P在直线m上(直线m经过点P)
1
、点A在直线m外(直线m不经过点A)
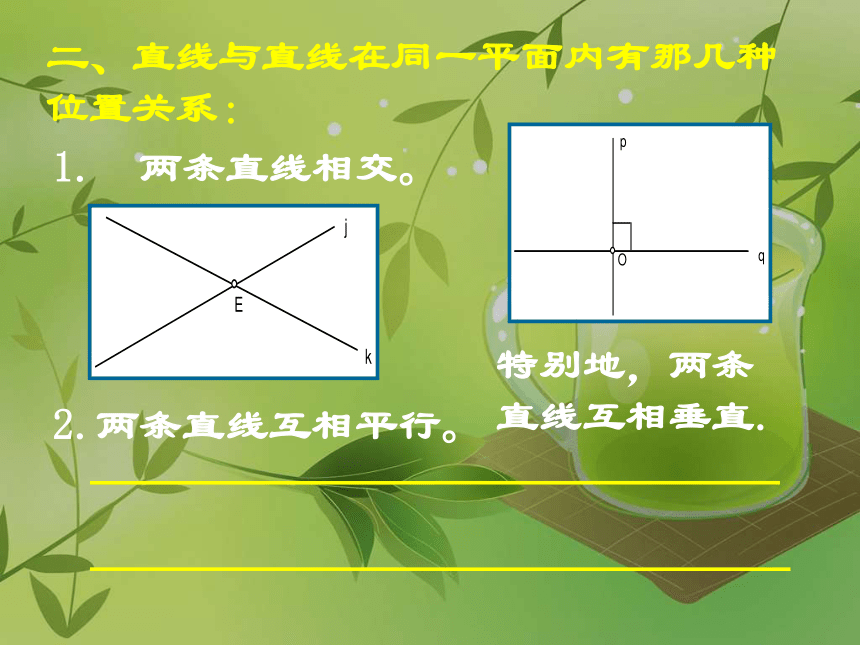
二、直线与直线在同一平面内有那几种位置关系:
1.
两条直线相交。
2.两条直线互相平行。
特别地,两条直线互相垂直.
相交线和平行线是我们日常生活和生产中经常见到的,研究它们对今后的学习、工作和生活都很有用。
我们先来研究相交线。
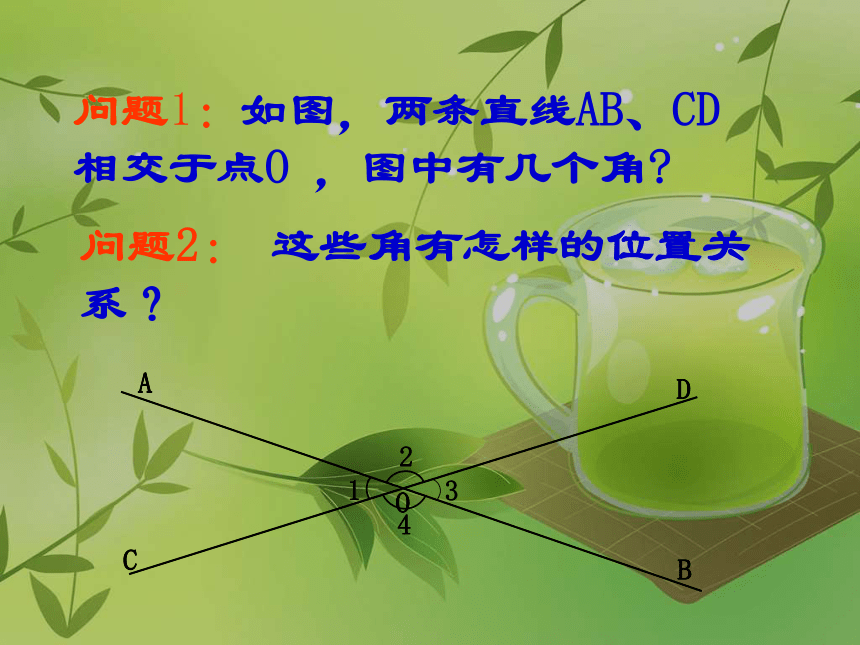
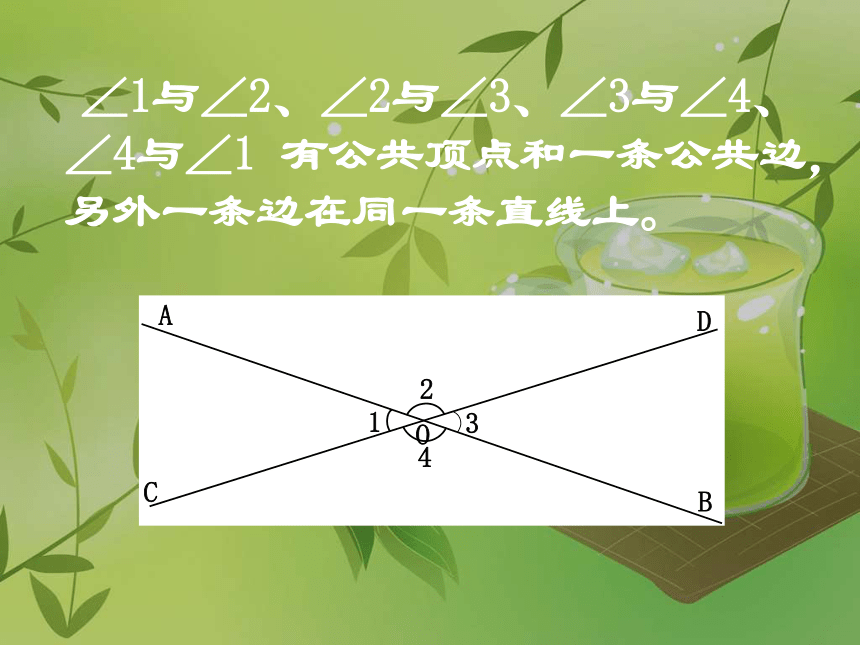
问题1:如图,两条直线AB、CD相交于点O
,图中有几个角?
问题2:
这些角有怎样的位置关系?
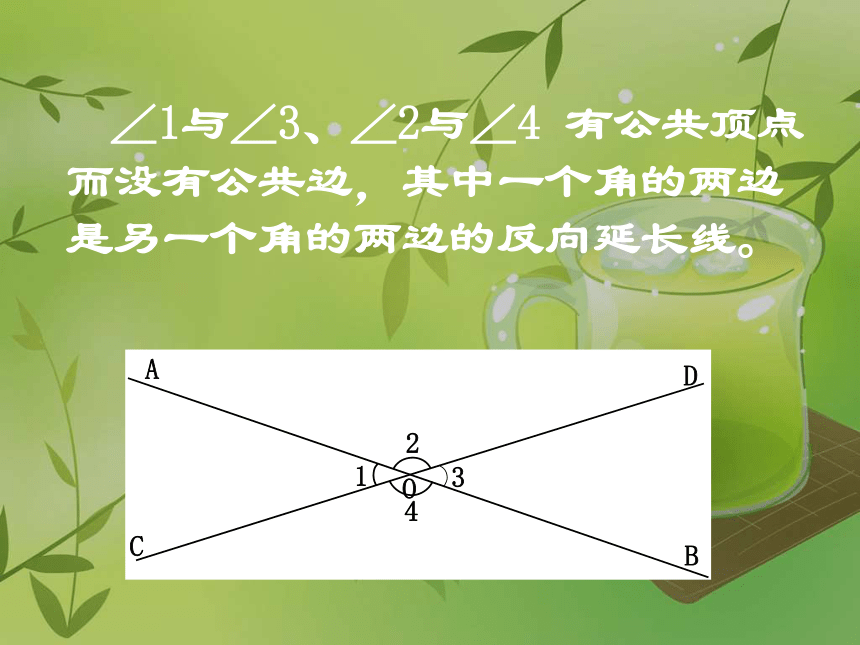
∠1与∠3、∠2与∠4
有公共顶点而没有公共边,其中一个角的两边是另一个角的两边的反向延长线。
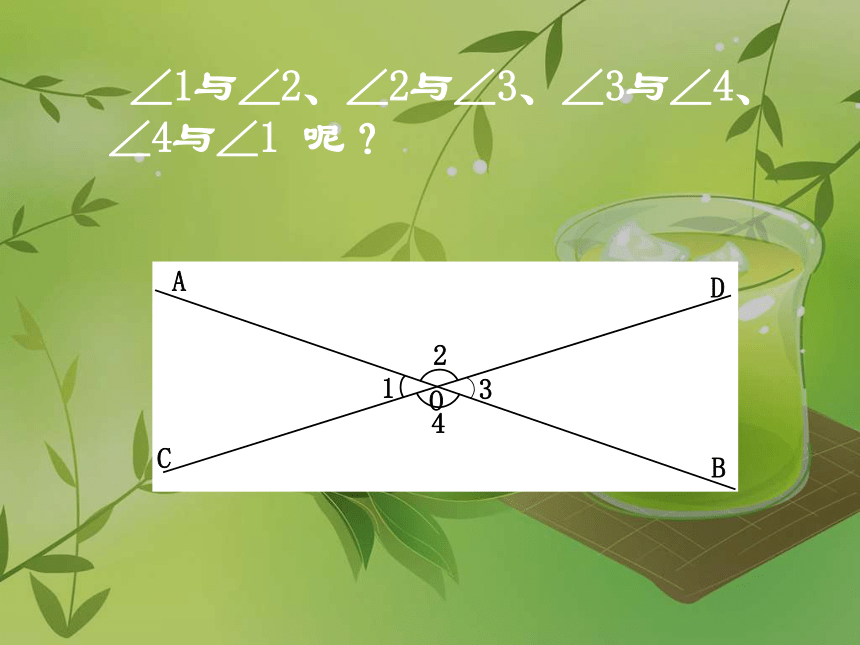
∠1与∠2、∠2与∠3、∠3与∠4、∠4与∠1
呢?
∠1与∠2、∠2与∠3、∠3与∠4、∠4与∠1
有公共顶点和一条公共边,另外一条边在同一条直线上。
1、
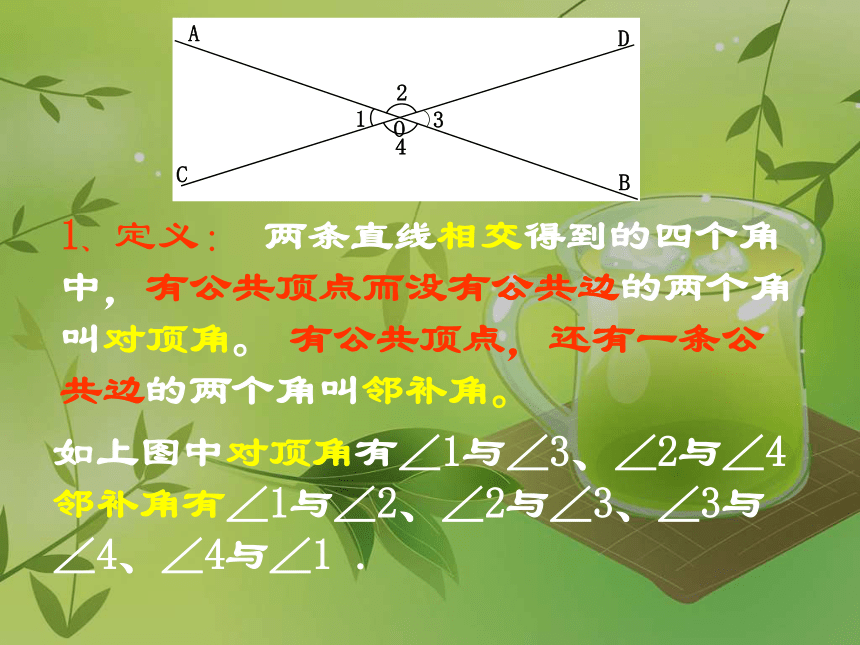
定义:
两条直线相交得到的四个角中,有公共顶点而没有公共边的两个角叫对顶角。
有公共顶点,还有一条公共边的两个角叫邻补角。
如上图中对顶角有∠1与∠3、∠2与∠4
邻补角有∠1与∠2、∠2与∠3、∠3与∠4、∠4与∠1
.
问题:
如图,O是直线AB上一点,则图中共有几个角?是邻补角吗?是对顶角吗?为什么?
C
A
B
O
邻补角也可以看成是一条直线与端点在这条直线上的一条射线组成的两个角。
1
练习1、下列各图中∠1、∠2是对顶角吗?为什么?
2
1
2
1
2
)
(
(
(
)
)
1
练习2、下列各图中∠1、∠2是邻补角吗?为什么?
2
1
2
1
2
)
(
(
(
)
(
练习3、下列各图中,有邻补角吗?有对顶角吗?如果有,请把它们指出来。
无对顶角,有两对邻补角:∠AOC与∠BOC
、
∠AOD与∠BOD
无对顶角,有两对邻补角:∠AOC与∠BOC
∠APD与∠BPD
A
A
B
B
C
C
D
D
O
O
P
(1)
(2)
3、如图,已知直线AE、BD相交于点C.
(1)图中哪些角是对顶角?
A
C
D
E
B
答:邻补角有四对:
∠ACB与∠ACD、∠ACB与∠BCE、
∠DCE与∠ACD、∠DCE与∠BCE.
答:对顶角有两对:
∠ACB与∠DCE、∠ACD与∠BCE.
(2)哪些角是邻补角?
问题3:邻补角一定互为补角。对顶角又有什么样的数量关系呢?
D
C
B
A
3
2
1
我们可以做下面的推理:
∵∠1与∠2互补,
∠2与∠3互补(邻补角定义),
∴∠1=∠3(同角的补角相等).
同理,∠2=∠4
.
2、对顶角性质:对顶角相等。
1、
对顶角相等。反过来,
相等的
两个角一定是对顶角吗?
2
3
4
2、邻补角互补。反过来,互补的角一定是邻补角吗?
例1:
已知直线AD与BE相交于点O,
∠COE
与
∠DOE
互余,
∠COE=62°,求∠AOB
的度数。
例2:直线AB,CD相交于点O,OE平分
∠BOD且∠AOC=∠BOC-30°
,
求∠AOE
例3:点O在直线AB上,且∠AOC=∠BOD
那么三点C,O,D在一直线上
吗?为什么?
A
B
C
D
O
E
(1)
A
B
C
D
O
E
(2)
无对顶角,有三对邻补角:
∠AOE与∠BOE
∠AOC与∠BOC
∠AOD与∠BOD
无对顶角,有三对邻补角:
∠AOC与∠
BOC
∠AOD与∠
BOD
∠AOE与∠BOE
2、下列说法是否正确?为什么?
(1)有公共顶点的两个角是对顶角。
答:不正确。如图,∠AOB与∠COD有
公共顶点O,但它们不是对顶角。
A
O
C
D
B
(2)有公共顶点而没有公共边的两个角是对顶角。
答:不正确。如上图,∠AOB与∠COD有公共顶点O,而且
没有公共边,但它们不是对顶角。
(3)相邻的两个角是邻补角。
答:不正确。如图,∠AOB
与∠BOC
有
公共顶点和一条公共边,是相邻的两
个角,但不互补,所以不是邻补角。
A
C
B
O
(4)
两条直线相交得到的四个角中,同一个角的两个邻角都是它的邻补角,是一对对顶角。
答:正确。如图,直线AB、CD相交于点O,
∠AOD的两个邻角是∠AOC和∠DOB,都是∠AOD的邻补角,是一对对顶角。其它角的邻角也如此。
O
D
C
B
A
3.如图,AB、CD、EF是经过点O的三条直线,说出:∠AOC,∠FOB,∠DOF,∠AOD,∠EOB
的对顶角分别是
,∠AOF
的邻补角是
、
A
B
C
E
F
D
O
∠BOD,∠AOE,∠COE,∠BOC,∠AOF
∠BOF
和∠AOE
小结
今天,我们学习了两直线相交这种位置关系的有关知识,要弄清对顶角和邻补角这两个重要概念以及“对顶角相等”这一重要性质,因为它们在我们今后的学习中经常用到;要学会从复杂的图形中分解出基本的图形,从而正确识别对顶角、邻补角,逐步训练和提高自己的识图能力和计算推理能力。
5.1
相交线
一、点与直线有哪几种位置关系:
·
·
A
P
m
2
、点
P在直线m上(直线m经过点P)
1
、点A在直线m外(直线m不经过点A)
二、直线与直线在同一平面内有那几种位置关系:
1.
两条直线相交。
2.两条直线互相平行。
特别地,两条直线互相垂直.
相交线和平行线是我们日常生活和生产中经常见到的,研究它们对今后的学习、工作和生活都很有用。
我们先来研究相交线。
问题1:如图,两条直线AB、CD相交于点O
,图中有几个角?
问题2:
这些角有怎样的位置关系?
∠1与∠3、∠2与∠4
有公共顶点而没有公共边,其中一个角的两边是另一个角的两边的反向延长线。
∠1与∠2、∠2与∠3、∠3与∠4、∠4与∠1
呢?
∠1与∠2、∠2与∠3、∠3与∠4、∠4与∠1
有公共顶点和一条公共边,另外一条边在同一条直线上。
1、
定义:
两条直线相交得到的四个角中,有公共顶点而没有公共边的两个角叫对顶角。
有公共顶点,还有一条公共边的两个角叫邻补角。
如上图中对顶角有∠1与∠3、∠2与∠4
邻补角有∠1与∠2、∠2与∠3、∠3与∠4、∠4与∠1
.
问题:
如图,O是直线AB上一点,则图中共有几个角?是邻补角吗?是对顶角吗?为什么?
C
A
B
O
邻补角也可以看成是一条直线与端点在这条直线上的一条射线组成的两个角。
1
练习1、下列各图中∠1、∠2是对顶角吗?为什么?
2
1
2
1
2
)
(
(
(
)
)
1
练习2、下列各图中∠1、∠2是邻补角吗?为什么?
2
1
2
1
2
)
(
(
(
)
(
练习3、下列各图中,有邻补角吗?有对顶角吗?如果有,请把它们指出来。
无对顶角,有两对邻补角:∠AOC与∠BOC
、
∠AOD与∠BOD
无对顶角,有两对邻补角:∠AOC与∠BOC
∠APD与∠BPD
A
A
B
B
C
C
D
D
O
O
P
(1)
(2)
3、如图,已知直线AE、BD相交于点C.
(1)图中哪些角是对顶角?
A
C
D
E
B
答:邻补角有四对:
∠ACB与∠ACD、∠ACB与∠BCE、
∠DCE与∠ACD、∠DCE与∠BCE.
答:对顶角有两对:
∠ACB与∠DCE、∠ACD与∠BCE.
(2)哪些角是邻补角?
问题3:邻补角一定互为补角。对顶角又有什么样的数量关系呢?
D
C
B
A
3
2
1
我们可以做下面的推理:
∵∠1与∠2互补,
∠2与∠3互补(邻补角定义),
∴∠1=∠3(同角的补角相等).
同理,∠2=∠4
.
2、对顶角性质:对顶角相等。
1、
对顶角相等。反过来,
相等的
两个角一定是对顶角吗?
2
3
4
2、邻补角互补。反过来,互补的角一定是邻补角吗?
例1:
已知直线AD与BE相交于点O,
∠COE
与
∠DOE
互余,
∠COE=62°,求∠AOB
的度数。
例2:直线AB,CD相交于点O,OE平分
∠BOD且∠AOC=∠BOC-30°
,
求∠AOE
例3:点O在直线AB上,且∠AOC=∠BOD
那么三点C,O,D在一直线上
吗?为什么?
A
B
C
D
O
E
(1)
A
B
C
D
O
E
(2)
无对顶角,有三对邻补角:
∠AOE与∠BOE
∠AOC与∠BOC
∠AOD与∠BOD
无对顶角,有三对邻补角:
∠AOC与∠
BOC
∠AOD与∠
BOD
∠AOE与∠BOE
2、下列说法是否正确?为什么?
(1)有公共顶点的两个角是对顶角。
答:不正确。如图,∠AOB与∠COD有
公共顶点O,但它们不是对顶角。
A
O
C
D
B
(2)有公共顶点而没有公共边的两个角是对顶角。
答:不正确。如上图,∠AOB与∠COD有公共顶点O,而且
没有公共边,但它们不是对顶角。
(3)相邻的两个角是邻补角。
答:不正确。如图,∠AOB
与∠BOC
有
公共顶点和一条公共边,是相邻的两
个角,但不互补,所以不是邻补角。
A
C
B
O
(4)
两条直线相交得到的四个角中,同一个角的两个邻角都是它的邻补角,是一对对顶角。
答:正确。如图,直线AB、CD相交于点O,
∠AOD的两个邻角是∠AOC和∠DOB,都是∠AOD的邻补角,是一对对顶角。其它角的邻角也如此。
O
D
C
B
A
3.如图,AB、CD、EF是经过点O的三条直线,说出:∠AOC,∠FOB,∠DOF,∠AOD,∠EOB
的对顶角分别是
,∠AOF
的邻补角是
、
A
B
C
E
F
D
O
∠BOD,∠AOE,∠COE,∠BOC,∠AOF
∠BOF
和∠AOE
小结
今天,我们学习了两直线相交这种位置关系的有关知识,要弄清对顶角和邻补角这两个重要概念以及“对顶角相等”这一重要性质,因为它们在我们今后的学习中经常用到;要学会从复杂的图形中分解出基本的图形,从而正确识别对顶角、邻补角,逐步训练和提高自己的识图能力和计算推理能力。
