人教版八年级数学下册课时作业:20.1.1 第1课时 平均数(Word版含解析)
文档属性
| 名称 | 人教版八年级数学下册课时作业:20.1.1 第1课时 平均数(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 232.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 00:00:00 | ||
图片预览


文档简介
20.1.1 第1课时 平均数
知识点1 算术平均数
1.7名学生的体重(单位:
kg)分别是40,42,43,45,47,47,58,则这组数据的平均数是( )
A.44
B.45
C.46
D.47
2.某中学举行校园歌手大赛,7位评委给选手小明的评分如下表:
评委
1
2
3
4
5
6
7
得分(分)
9.8
9.5
9.7
9.8
9.4
9.5
9.4
比赛的计分方法如下:去掉一个最高分,去掉一个最低分,其余分数的平均值作为该选手的最后得分,则小明的最后得分为
( )
A.9.56分
B.9.57分
C.9.58分
D.9.59分
3.睡眠是评价人类健康水平的一项重要指标,充足的睡眠是青少年健康成长的必要条件之一.小强同学通过问卷调查的方式了解到本班三名同学某天的睡眠时间分别为7.8小时,8.6小时,8.8小时,则这三名同学该天的平均睡眠时间是 小时.?
4.一名同学进行五次投实心球的练习,每次投出的成绩如下表:
投实心球次序
1
2
3
4
5
成绩(m)
10.5
10.2
10.3
10.6
10.4
求该同学这五次投实心球的平均成绩.
知识点2 加权平均数
5.在某公司的面试中,李明的得分情况为:个人形象89分,工作能力93分,交际能力83分.已知个人形象、工作能力和交际能力的权重比为3∶3∶4,则李明的最终成绩是
( )
A.88.33分
B.88分
C.87.8分
D.265分
6.为鼓励市民珍惜每一滴水,某居委会表扬了100户节约用水模范户,这100户居民6月份节约用水的情况如下表:
每户节水量(单位:t)
1
1.2
1.5
节水户数
52
30
18
则6月份这100户居民平均节约用水的吨数为
( )
A.1.20
t
B.1.15
t
C.1.05
t
D.1
t
7.为了满足顾客的需求,某商场将5千克奶糖、3千克酥心糖和2千克水果糖混合成什锦糖出售.已知奶糖的售价为每千克40元,酥心糖的售价为每千克20元,水果糖的售价为每千克15元,混合后什锦糖的售价应为每千克
( )
A.25元
B.28.5元
C.29元
D.34.5元
8.某校拟招聘一名优秀数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如下表所示,综合成绩按照笔试占60%、面试占40%进行计算,学校录取综合成绩得分最高者,求被录取教师的综合成绩.
教师
成绩
甲
乙
丙
笔试
80分
82分
78分
面试
76分
74分
78分
9.若一组数据3,4,5,x,6,7的平均数是5,则x的值是
( )
A.4
B.5
C.6
D.7
10.某企业对一工人在五个工作日里生产零件的数量进行调查,并绘制了如图所示的折线统计图,则在这五天里,该工人每天生产零件的平均数是 个.?
11.某班40名学生的某次数学测验成绩统计如下表:
成绩(分)
50
60
70
80
90
100
人数(人)
2
x
10
y
4
2
若这个班该次数学测验的平均成绩是69分,则x= ,y= .?
12.某校要招聘一名教师,现有甲、乙、丙三人通过专业知识、讲课、答辩三项测试,他们各自的成绩如下表所示(单位:分):
应聘者
专业知识
讲课
答辩
甲
70
85
80
乙
90
85
75
丙
80
90
85
按照招聘简章要求,对专业知识、讲课、答辩三项赋权5∶4∶1,请计算三名应聘者的平均成绩,从成绩看,应该录取谁?
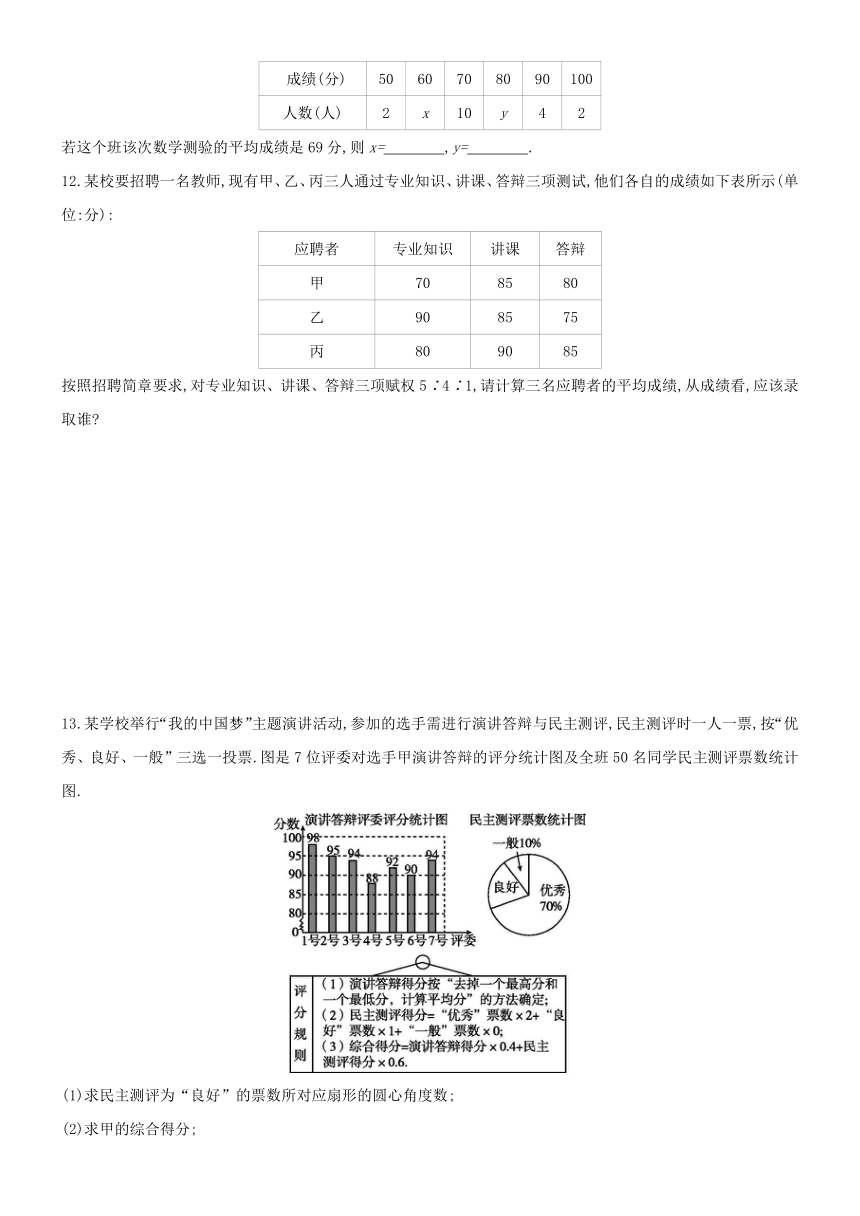
13.某学校举行“我的中国梦”主题演讲活动,参加的选手需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.图是7位评委对选手甲演讲答辩的评分统计图及全班50名同学民主测评票数统计图.
(1)求民主测评为“良好”的票数所对应扇形的圆心角度数;
(2)求甲的综合得分;
(3)在活动中,选手乙的民主测评得分为82分,若他的综合得分不低于甲的综合得分,则乙的演讲答辩得分至少为多少分?
答案
1.C 解析:
平均数为(40+42+43+45+47+47+58)÷7=322÷7=46.
2.C 解析:
去掉一个9.8分和一个9.4分,然后计算剩余五个数的平均数,所以小明的最后得分==9.58(分).故选C.
3.8.4 解析:
根据题意,得(7.8+8.6+8.8)÷3=8.4(时),
则这三名同学该天的平均睡眠时间是8.4小时.
4.解:该同学这五次投实心球的平均成绩为
=10+×(0.5+0.2+0.3+0.6+0.4)=10+0.4=10.4(m).
5.C 解析:
=87.8(分).故选C.
6.B 解析:
(52×1+30×1.2+18×1.5)÷100=1.15(t).故选B.
7.C 解析:
根据题意,得(40×5+20×3+15×2)÷(5+3+2)=29(元),即混合后什锦糖的售价应为每千克29元.故选C.
8.解:甲的综合成绩为80×60%+76×40%=78.4(分),乙的综合成绩为82×60%+74×40%=78.8(分),丙的综合成绩为78×60%+78×40%=78(分).因为78<78.4<78.8,所以被录取的教师为乙,其综合成绩为78.8分.
9.B 解析:
因为=5,所以x=5.故选B.
10.34 解析:
由图可知这组数据是36,34,31,34,35,
故=×(36+34+31+34+35)=×170=34.因此答案为34.
11.18 4 解析:
依题意得,50×2+60x+70×10+80y+90×4+100×2=69×40,
即3x+4y=70①,
x+y+2+10+4+2=40,
即x+y=22②.
联立①②,解得
故答案为18,4.
12.解:甲的平均成绩为=77(分);
乙的平均成绩为=86.5(分);
丙的平均成绩为=84.5(分).
因为乙的平均成绩最高,所以应该录取乙.
13.解:(1)民主测评为“良好”的票数所对应扇形的圆心角度数是(1-10%-70%)×360°=72°.
(2)演讲答辩得分为(95+94+92+90+94)÷5=93(分),
民主测评得分为50×70%×2+50×20%×1=80(分),
所以甲的综合得分为93×0.4+80×0.6=85.2(分).
(3)设乙的演讲答辩得分为x分.
根据题意,得82×0.6+0.4x≥85.2,解得x≥90.
答:乙的演讲答辩得分至少为90分.
知识点1 算术平均数
1.7名学生的体重(单位:
kg)分别是40,42,43,45,47,47,58,则这组数据的平均数是( )
A.44
B.45
C.46
D.47
2.某中学举行校园歌手大赛,7位评委给选手小明的评分如下表:
评委
1
2
3
4
5
6
7
得分(分)
9.8
9.5
9.7
9.8
9.4
9.5
9.4
比赛的计分方法如下:去掉一个最高分,去掉一个最低分,其余分数的平均值作为该选手的最后得分,则小明的最后得分为
( )
A.9.56分
B.9.57分
C.9.58分
D.9.59分
3.睡眠是评价人类健康水平的一项重要指标,充足的睡眠是青少年健康成长的必要条件之一.小强同学通过问卷调查的方式了解到本班三名同学某天的睡眠时间分别为7.8小时,8.6小时,8.8小时,则这三名同学该天的平均睡眠时间是 小时.?
4.一名同学进行五次投实心球的练习,每次投出的成绩如下表:
投实心球次序
1
2
3
4
5
成绩(m)
10.5
10.2
10.3
10.6
10.4
求该同学这五次投实心球的平均成绩.
知识点2 加权平均数
5.在某公司的面试中,李明的得分情况为:个人形象89分,工作能力93分,交际能力83分.已知个人形象、工作能力和交际能力的权重比为3∶3∶4,则李明的最终成绩是
( )
A.88.33分
B.88分
C.87.8分
D.265分
6.为鼓励市民珍惜每一滴水,某居委会表扬了100户节约用水模范户,这100户居民6月份节约用水的情况如下表:
每户节水量(单位:t)
1
1.2
1.5
节水户数
52
30
18
则6月份这100户居民平均节约用水的吨数为
( )
A.1.20
t
B.1.15
t
C.1.05
t
D.1
t
7.为了满足顾客的需求,某商场将5千克奶糖、3千克酥心糖和2千克水果糖混合成什锦糖出售.已知奶糖的售价为每千克40元,酥心糖的售价为每千克20元,水果糖的售价为每千克15元,混合后什锦糖的售价应为每千克
( )
A.25元
B.28.5元
C.29元
D.34.5元
8.某校拟招聘一名优秀数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如下表所示,综合成绩按照笔试占60%、面试占40%进行计算,学校录取综合成绩得分最高者,求被录取教师的综合成绩.
教师
成绩
甲
乙
丙
笔试
80分
82分
78分
面试
76分
74分
78分
9.若一组数据3,4,5,x,6,7的平均数是5,则x的值是
( )
A.4
B.5
C.6
D.7
10.某企业对一工人在五个工作日里生产零件的数量进行调查,并绘制了如图所示的折线统计图,则在这五天里,该工人每天生产零件的平均数是 个.?
11.某班40名学生的某次数学测验成绩统计如下表:
成绩(分)
50
60
70
80
90
100
人数(人)
2
x
10
y
4
2
若这个班该次数学测验的平均成绩是69分,则x= ,y= .?
12.某校要招聘一名教师,现有甲、乙、丙三人通过专业知识、讲课、答辩三项测试,他们各自的成绩如下表所示(单位:分):
应聘者
专业知识
讲课
答辩
甲
70
85
80
乙
90
85
75
丙
80
90
85
按照招聘简章要求,对专业知识、讲课、答辩三项赋权5∶4∶1,请计算三名应聘者的平均成绩,从成绩看,应该录取谁?
13.某学校举行“我的中国梦”主题演讲活动,参加的选手需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.图是7位评委对选手甲演讲答辩的评分统计图及全班50名同学民主测评票数统计图.
(1)求民主测评为“良好”的票数所对应扇形的圆心角度数;
(2)求甲的综合得分;
(3)在活动中,选手乙的民主测评得分为82分,若他的综合得分不低于甲的综合得分,则乙的演讲答辩得分至少为多少分?
答案
1.C 解析:
平均数为(40+42+43+45+47+47+58)÷7=322÷7=46.
2.C 解析:
去掉一个9.8分和一个9.4分,然后计算剩余五个数的平均数,所以小明的最后得分==9.58(分).故选C.
3.8.4 解析:
根据题意,得(7.8+8.6+8.8)÷3=8.4(时),
则这三名同学该天的平均睡眠时间是8.4小时.
4.解:该同学这五次投实心球的平均成绩为
=10+×(0.5+0.2+0.3+0.6+0.4)=10+0.4=10.4(m).
5.C 解析:
=87.8(分).故选C.
6.B 解析:
(52×1+30×1.2+18×1.5)÷100=1.15(t).故选B.
7.C 解析:
根据题意,得(40×5+20×3+15×2)÷(5+3+2)=29(元),即混合后什锦糖的售价应为每千克29元.故选C.
8.解:甲的综合成绩为80×60%+76×40%=78.4(分),乙的综合成绩为82×60%+74×40%=78.8(分),丙的综合成绩为78×60%+78×40%=78(分).因为78<78.4<78.8,所以被录取的教师为乙,其综合成绩为78.8分.
9.B 解析:
因为=5,所以x=5.故选B.
10.34 解析:
由图可知这组数据是36,34,31,34,35,
故=×(36+34+31+34+35)=×170=34.因此答案为34.
11.18 4 解析:
依题意得,50×2+60x+70×10+80y+90×4+100×2=69×40,
即3x+4y=70①,
x+y+2+10+4+2=40,
即x+y=22②.
联立①②,解得
故答案为18,4.
12.解:甲的平均成绩为=77(分);
乙的平均成绩为=86.5(分);
丙的平均成绩为=84.5(分).
因为乙的平均成绩最高,所以应该录取乙.
13.解:(1)民主测评为“良好”的票数所对应扇形的圆心角度数是(1-10%-70%)×360°=72°.
(2)演讲答辩得分为(95+94+92+90+94)÷5=93(分),
民主测评得分为50×70%×2+50×20%×1=80(分),
所以甲的综合得分为93×0.4+80×0.6=85.2(分).
(3)设乙的演讲答辩得分为x分.
根据题意,得82×0.6+0.4x≥85.2,解得x≥90.
答:乙的演讲答辩得分至少为90分.
