人教版七年级下册数学7.1.2平面直角坐标系(平面直角坐标系相关概念) (共16张)
文档属性
| 名称 | 人教版七年级下册数学7.1.2平面直角坐标系(平面直角坐标系相关概念) (共16张) |  | |
| 格式 | pptx | ||
| 文件大小 | 162.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 13:01:24 | ||
图片预览




文档简介
7.1.2平面直角坐标系
勒内笛卡尔,法国人,出生于1596年3月31日,逝世于1650年2月11日。是一名哲学家、数学家、物理学家。主要成就是几何坐标体系公式化。
笛卡尔最早引入坐标系,用代数方法研究几何图形。他对现代数学的发展做出了重要的贡献,因将几何坐标体系公式化,而被认为是解析几何之父。
1619年,笛卡尔在部队服役。一天,他因病躺在了床上,无所事事的他抬头望着天花板,一只小小的蜘蛛从墙角慢慢地爬过来,吐丝结网,忙个不停。从东爬到西,从南爬到北。要结一张网,小蜘蛛该走多少路啊。笛卡尔突发奇想,算一算蜘蛛走过的路程。他先把蜘蛛看成是一个点,这个点离墙角多远,离墙的两边多远,他思考着,计算着,病中的他睡着了。梦中的他继续在数学的广阔天地中驰骋,好像悟出了什么,又看到了什么。大梦醒来的笛卡尔茅塞顿开,一种新的思想初露端倪:在互相垂直的两条直线下,一个点可以用到这两条线的距离,也就是两个数来表示,这个点的位置就确定了。他恍然大悟:“啊!可以像蜘蛛一样用网格确定事物的位置啊!”
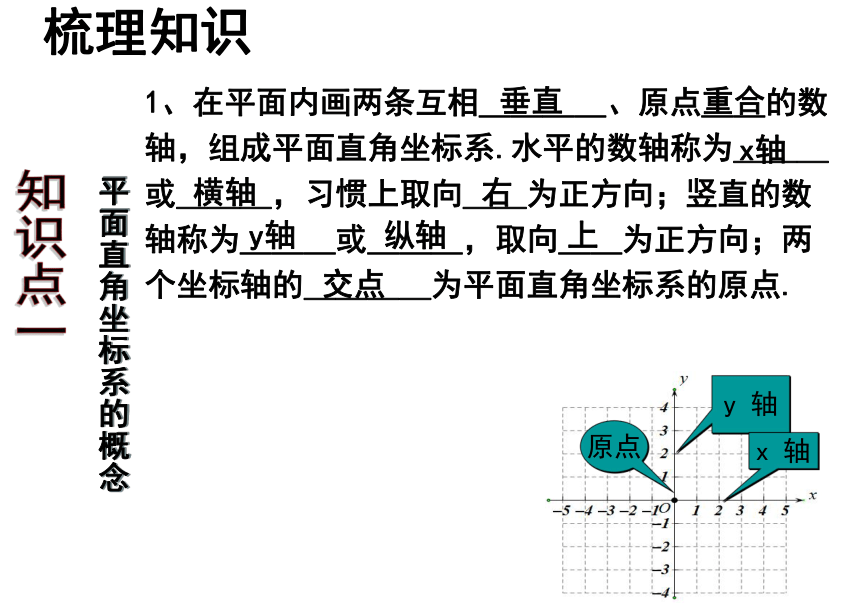
1、在平面内画两条互相____、原点__的数轴,组成平面直角坐标系.水平的数轴称为___或___,习惯上取向__为正方向;竖直的数轴称为___或___,取向__为正方向;两个坐标轴的____为平面直角坐标系的原点.
原点
y 轴
x 轴
上
纵轴
y轴
右
横轴
x轴
重合
垂直
交点
知识点一
平面直角坐标系的概念
梳理知识
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B
梳理知识
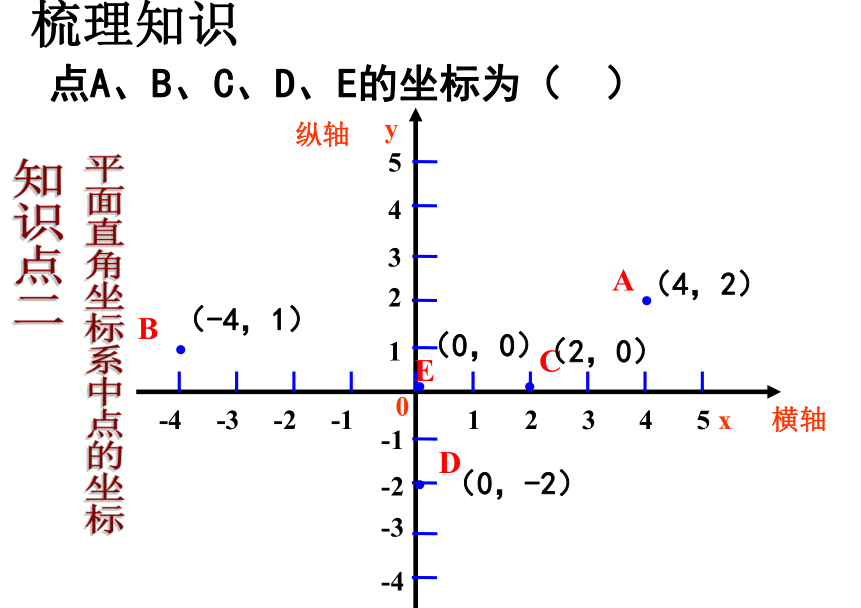
点A、B、C、D、E的坐标为( )
平面直角坐标系中点的坐标
知识点二
·
C
D
·
E
·
·
(4,2)
(-4,1)
(2,0)
(0,-2)
(0,0)
x
横轴
坐标(2,3),(3,2),(-2,1),
(-4,-3) (1,-2)
分别表示哪些点?
0
1
2
3
4
5
-4
-3
-2
-1
·
C
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
·
B
·
A
·
E
·
D
坐标平面上的点
有序数对(坐标)
一 一对应
梳理知识
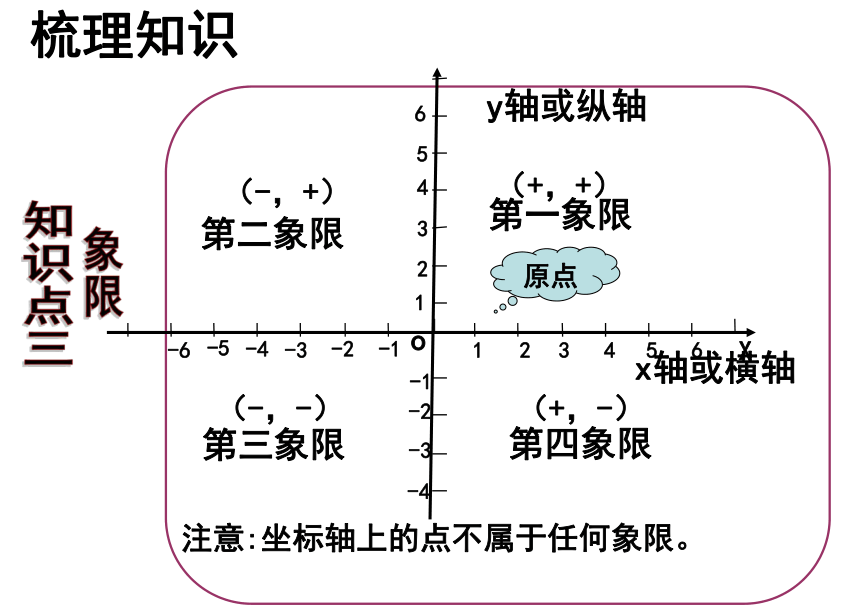
知识点三
象限
5
-2
-3
-4
-1
3
2
4
1
6
y轴或纵轴
x轴或横轴
原点
第一象限
第二象限
第三象限
第四象限
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
注意:坐标轴上的点不属于任何象限。
梳理知识
(+,+)
(-,+)
(-,-)
(+,-)
下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
梳理知识
答疑解惑
二、1、A(1,1)B(4,3)C(-3,2)
2、如图
D
E
3、四,三,y,x。
4、(5,-4)
5、a=-1
三、1、(5,4)或(5,-4)
或(-5,4)或(-5,-4)
2、a=-2,b=3
3、B
4、(1)a=3 (2)a=-0.5
5、坐标轴上
1.(2005年大连)在平面直角坐标系内,下列各点
在第四象限的是( )(A层)
A.(2,1) B.(-2,1) C.(-3,-5) D.(3,-5)
2.点P(a,1)在第一象限,那么点A(a+1,-1)在
第( )象限(B、C层)
A.第一象限B.第二象限C.第三象限D.第四象限
3.在平面直角坐标系中,点(-2,m2+1)一定在( )
(B、C层)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
理解运用
4、(a,b)在x轴上,b= _______________(A层)
5、点A在y轴上,距离原点4个单位长度,则A点的坐标是 _______________。(B、C层)
理解运用
1、已知点P(a-1,a-5)(A、B层)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
③若a=-3 ,则点P在第 象限内;
④若a=3,则点P在第 象限内.
2、若点P(x,y)的坐标满足xy﹤0,且在x轴上方,则点P在第 象限.(B、C层)
3、如果a-b<0,且ab<0,那么点(a,b)在( )(B、C层)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4、实数x,y满足(x-1)2+|y|=0,则点P(x,y)在( )
巩固提升
小组讨论
如果点A(n, 1-n),那么点A一定不在第几象限?
游戏(沙场秋点兵)
规则:以本班某个同学为坐标原点,建立全班范围的平面直角坐标系,他所在的行、列为坐标轴,规定正方向后建立坐标系,教师当教官,点到谁的坐标谁起立。
小结
同学们,其实我们每个人的人生就是一个以时间为横轴,以人生价值为纵轴的平面直角坐标系。我相信同学们一定能用自己的勤奋和智慧在这个坐标系中画出一个个光彩夺目的点,勾画出辉煌的人生。
作业
必做:1、P68-练习1、2
2、观看微课视频,阅读教材, 完成自主学习任务单上的问题。
选做:P69-4、P71-10
勒内笛卡尔,法国人,出生于1596年3月31日,逝世于1650年2月11日。是一名哲学家、数学家、物理学家。主要成就是几何坐标体系公式化。
笛卡尔最早引入坐标系,用代数方法研究几何图形。他对现代数学的发展做出了重要的贡献,因将几何坐标体系公式化,而被认为是解析几何之父。
1619年,笛卡尔在部队服役。一天,他因病躺在了床上,无所事事的他抬头望着天花板,一只小小的蜘蛛从墙角慢慢地爬过来,吐丝结网,忙个不停。从东爬到西,从南爬到北。要结一张网,小蜘蛛该走多少路啊。笛卡尔突发奇想,算一算蜘蛛走过的路程。他先把蜘蛛看成是一个点,这个点离墙角多远,离墙的两边多远,他思考着,计算着,病中的他睡着了。梦中的他继续在数学的广阔天地中驰骋,好像悟出了什么,又看到了什么。大梦醒来的笛卡尔茅塞顿开,一种新的思想初露端倪:在互相垂直的两条直线下,一个点可以用到这两条线的距离,也就是两个数来表示,这个点的位置就确定了。他恍然大悟:“啊!可以像蜘蛛一样用网格确定事物的位置啊!”
1、在平面内画两条互相____、原点__的数轴,组成平面直角坐标系.水平的数轴称为___或___,习惯上取向__为正方向;竖直的数轴称为___或___,取向__为正方向;两个坐标轴的____为平面直角坐标系的原点.
原点
y 轴
x 轴
上
纵轴
y轴
右
横轴
x轴
重合
垂直
交点
知识点一
平面直角坐标系的概念
梳理知识
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B
梳理知识
点A、B、C、D、E的坐标为( )
平面直角坐标系中点的坐标
知识点二
·
C
D
·
E
·
·
(4,2)
(-4,1)
(2,0)
(0,-2)
(0,0)
x
横轴
坐标(2,3),(3,2),(-2,1),
(-4,-3) (1,-2)
分别表示哪些点?
0
1
2
3
4
5
-4
-3
-2
-1
·
C
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
·
B
·
A
·
E
·
D
坐标平面上的点
有序数对(坐标)
一 一对应
梳理知识
知识点三
象限
5
-2
-3
-4
-1
3
2
4
1
6
y轴或纵轴
x轴或横轴
原点
第一象限
第二象限
第三象限
第四象限
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
注意:坐标轴上的点不属于任何象限。
梳理知识
(+,+)
(-,+)
(-,-)
(+,-)
下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
梳理知识
答疑解惑
二、1、A(1,1)B(4,3)C(-3,2)
2、如图
D
E
3、四,三,y,x。
4、(5,-4)
5、a=-1
三、1、(5,4)或(5,-4)
或(-5,4)或(-5,-4)
2、a=-2,b=3
3、B
4、(1)a=3 (2)a=-0.5
5、坐标轴上
1.(2005年大连)在平面直角坐标系内,下列各点
在第四象限的是( )(A层)
A.(2,1) B.(-2,1) C.(-3,-5) D.(3,-5)
2.点P(a,1)在第一象限,那么点A(a+1,-1)在
第( )象限(B、C层)
A.第一象限B.第二象限C.第三象限D.第四象限
3.在平面直角坐标系中,点(-2,m2+1)一定在( )
(B、C层)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
理解运用
4、(a,b)在x轴上,b= _______________(A层)
5、点A在y轴上,距离原点4个单位长度,则A点的坐标是 _______________。(B、C层)
理解运用
1、已知点P(a-1,a-5)(A、B层)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
③若a=-3 ,则点P在第 象限内;
④若a=3,则点P在第 象限内.
2、若点P(x,y)的坐标满足xy﹤0,且在x轴上方,则点P在第 象限.(B、C层)
3、如果a-b<0,且ab<0,那么点(a,b)在( )(B、C层)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4、实数x,y满足(x-1)2+|y|=0,则点P(x,y)在( )
巩固提升
小组讨论
如果点A(n, 1-n),那么点A一定不在第几象限?
游戏(沙场秋点兵)
规则:以本班某个同学为坐标原点,建立全班范围的平面直角坐标系,他所在的行、列为坐标轴,规定正方向后建立坐标系,教师当教官,点到谁的坐标谁起立。
小结
同学们,其实我们每个人的人生就是一个以时间为横轴,以人生价值为纵轴的平面直角坐标系。我相信同学们一定能用自己的勤奋和智慧在这个坐标系中画出一个个光彩夺目的点,勾画出辉煌的人生。
作业
必做:1、P68-练习1、2
2、观看微课视频,阅读教材, 完成自主学习任务单上的问题。
选做:P69-4、P71-10
