人教版八年级数学下册课时作业:18.2.3 正方形(Word版 含解析)
文档属性
| 名称 | 人教版八年级数学下册课时作业:18.2.3 正方形(Word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 175.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 00:00:00 | ||
图片预览


文档简介
18.2.3 正方形
知识点
1 正方形的概念及性质
1.如图,已知正方形ABCD的两条对角线相交于点O,那么图中等腰直角三角形共有( )
A.4个
B.6个
C.8个
D.10个
2.平行四边形、矩形、菱形、正方形共有的性质是
( )
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对角形互相垂直平分
3.若正方形的一条对角线的长为4,则这个正方形的面积是
( )
A.8
B.4
C.8
D.16
4.如图,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠BCP的度数是( )
A.45°
B.22.5°
C.67.5°
D.75°
5.如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF.
求证:(1)△ABE≌△BCF;
(2)AE⊥BF.
知识点
2 正方形的判定
6.下列判断中,正确的是
( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线互相垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
7.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.①②
B.②③
C.①③
D.②④
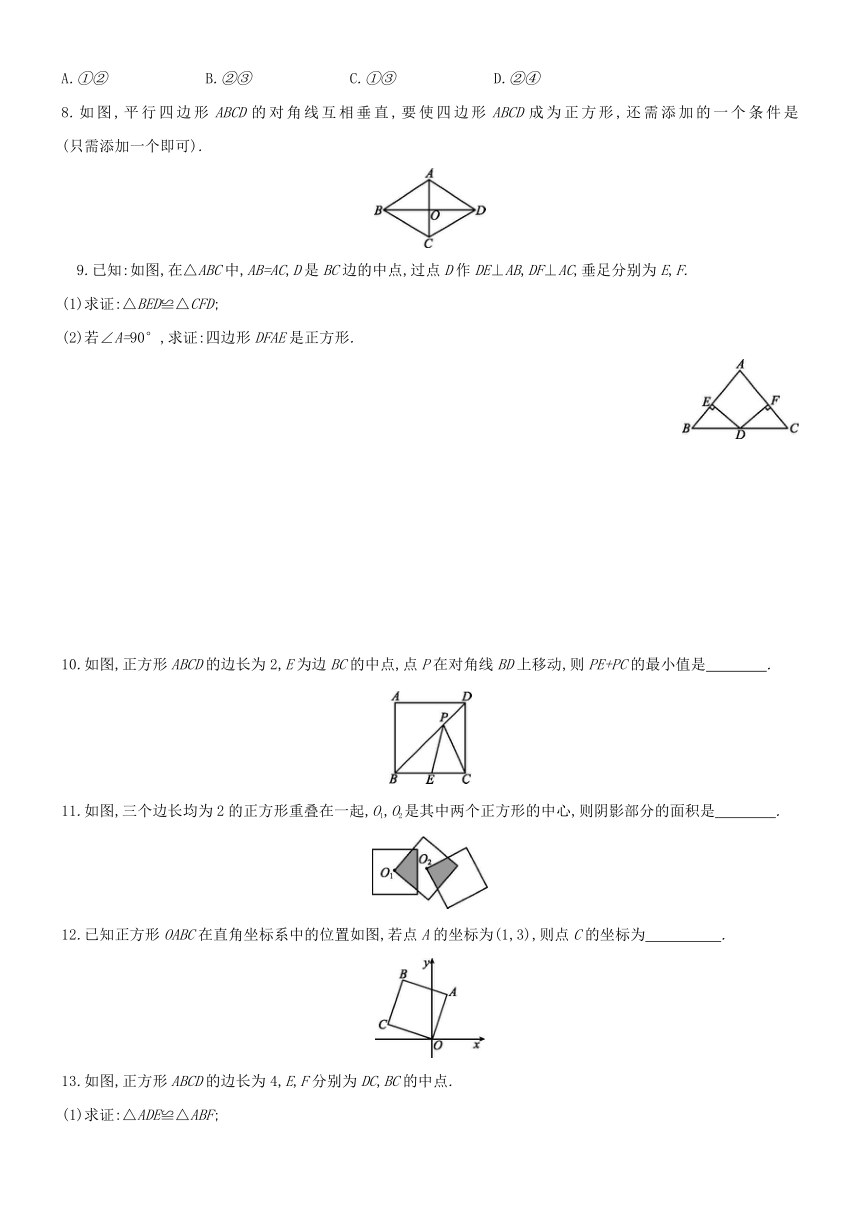
8.如图,平行四边形ABCD的对角线互相垂直,要使四边形ABCD成为正方形,还需添加的一个条件是 (只需添加一个即可).?
9.已知:如图,在△ABC中,AB=AC,D是BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
10.如图,正方形ABCD的边长为2,E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是 .?
11.如图,三个边长均为2的正方形重叠在一起,O1,O2是其中两个正方形的中心,则阴影部分的面积是 .?
12.已知正方形OABC在直角坐标系中的位置如图,若点A的坐标为(1,3),则点C的坐标为 .?
13.如图,正方形ABCD的边长为4,E,F分别为DC,BC的中点.
(1)求证:△ADE≌△ABF;
(2)求△AEF的面积.
14.如图,在四边形ABCD中,AB=CB,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
15.四边形ABCD为矩形,G是AB上的任意一点,CE⊥DG于点E.
(1)如图①,若AB=BC,AF∥CE,且交DG于点F,求证:DF-AF=EF;
(2)如图②,若AB=BC,G是AB的中点,求的值.
答案
1.C 解析:
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠BAD=90°,OA=OB=OC=OD,AC⊥BD,
∴△ABC,△ADC,△ABD,△BCD,△AOB,△BOC,△AOD,△COD都是等腰直角三角形.
故选C.
2.B 解析:
A.只有矩形、正方形的对角线相等,故本选项错误;B.平行四边形、矩形、菱形、正方形的对角线都互相平分,故本选项正确;C.只有菱形、正方形的对角线互相垂直,故本选项错误;D.只有菱形、正方形的对角线互相垂直平分,故本选项错误.故选B.
3.A 解析:
∵正方形的一条对角线长为4,
∴这个正方形的面积=×4×4=8.故选A.
4.C 解析:
∵四边形ABCD是正方形,
∴∠DBC=45°.
∵BP=BC,∴∠BCP=∠BPC=(180°-45°)=67.5°.
5.证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠C=90°.
在△ABE和△BCF中,
∴△ABE≌△BCF.
(2)如图,设AE与BF交于点O.
∵△ABE≌△BCF,
∴∠BAE=∠CBF.
∵∠ABE=90°,∴∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,
∴∠BOE=90°,即AE⊥BF.
6.D 解析:
A错误,四边相等的四边形是菱形.B错误,四角相等的四边形是矩形.C错误,对角线互相垂直的平行四边形是菱形.D正确,对角线互相垂直平分且相等的四边形是正方形.故选D.
7.B 解析:
添加①可得平行四边形ABCD是菱形,添加②可得平行四边形ABCD是矩形,添加③可得平行四边形ABCD是矩形,添加④可得平行四边形ABCD是菱形,所以选②③不能使得平行四边形ABCD是正方形.
8.∠ABC=90°(答案不唯一)
9.证明:(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC边的中点,∴BD=CD,
∴△BED≌△CFD.
(2)∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
又∵∠A=90°,∴四边形DFAE是矩形.
∵△BED≌△CFD,
∴DE=DF,∴矩形DFAE是正方形.
10.
11.2
12.(-3,1) 解析:
如图,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,则∠OAD+∠AOD=90°.
∵四边形OABC是正方形,
∴OA=CO,∠AOC=90°,
∴∠COE+∠AOD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,
∴△AOD≌△OCE(AAS),
∴OE=AD=3,CE=OD=1.
∵点C在第二象限,
∴点C的坐标为(-3,1).
故答案为(-3,1).
13.解:(1)证明:∵四边形ABCD为正方形,
∴AB=AD=DC=BC,∠D=∠B=90°.
∵E,F分别为DC,BC的中点,
∴DE=DC,BF=BC,∴DE=BF.
在△ADE和△ABF中,
∴△ADE≌△ABF(SAS).
(2)由题意知AB=AD=4,
DE=BF=CE=CF=×4=2,
∴S△AEF=S正方形ABCD-S△ABF-S△ADE-S△CEF=4×4-×4×2-×4×2-×2×2=6.
14.证明:(1)∵BD平分∠ABC,
∴∠ABD=∠CBD.
又∵AB=CB,BD=BD,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB.
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°.
又∵∠ADC=90°,
∴四边形MPND是矩形.
∵∠ADB=∠CDB,PM⊥AD,PN⊥CD,
∴PM=PN,
∴四边形MPND是正方形.
15.解:(1)证明:∵四边形ABCD是矩形,AB=BC,
∴四边形ABCD是正方形,∠ADC=90°,
∴AD=DC,∠CDE+∠ADF=90°.
∵CE⊥DG,AF∥CE,
∴∠CED=∠CEF=∠DFA=90°.
∵∠DAF+∠ADF=90°,
∴∠CDE=∠DAF,
∴△AFD≌△DEC(AAS),∴AF=DE,
∴DF-AF=DF-DE=EF.
(2)延长DG,CB相交于点H,如图.
∵四边形ABCD是矩形,AB=BC,
∴四边形ABCD是正方形,
∴AD=AB=BC.
∵G是AB的中点,
∴AG=BG,
∴=.
在△ADG和△BHG中,
∴△ADG≌△BHG(ASA),
∴AD=BH.
∵AD=BC,
∴BH=BC,
即B是CH的中点.
∵CE⊥DG,∴∠CEH=90°,
即△CEH是直角三角形,
∴BE=CH=BC,∴BE=AB,
∴==.
知识点
1 正方形的概念及性质
1.如图,已知正方形ABCD的两条对角线相交于点O,那么图中等腰直角三角形共有( )
A.4个
B.6个
C.8个
D.10个
2.平行四边形、矩形、菱形、正方形共有的性质是
( )
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对角形互相垂直平分
3.若正方形的一条对角线的长为4,则这个正方形的面积是
( )
A.8
B.4
C.8
D.16
4.如图,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠BCP的度数是( )
A.45°
B.22.5°
C.67.5°
D.75°
5.如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF.
求证:(1)△ABE≌△BCF;
(2)AE⊥BF.
知识点
2 正方形的判定
6.下列判断中,正确的是
( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线互相垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
7.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.①②
B.②③
C.①③
D.②④
8.如图,平行四边形ABCD的对角线互相垂直,要使四边形ABCD成为正方形,还需添加的一个条件是 (只需添加一个即可).?
9.已知:如图,在△ABC中,AB=AC,D是BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
10.如图,正方形ABCD的边长为2,E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是 .?
11.如图,三个边长均为2的正方形重叠在一起,O1,O2是其中两个正方形的中心,则阴影部分的面积是 .?
12.已知正方形OABC在直角坐标系中的位置如图,若点A的坐标为(1,3),则点C的坐标为 .?
13.如图,正方形ABCD的边长为4,E,F分别为DC,BC的中点.
(1)求证:△ADE≌△ABF;
(2)求△AEF的面积.
14.如图,在四边形ABCD中,AB=CB,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
15.四边形ABCD为矩形,G是AB上的任意一点,CE⊥DG于点E.
(1)如图①,若AB=BC,AF∥CE,且交DG于点F,求证:DF-AF=EF;
(2)如图②,若AB=BC,G是AB的中点,求的值.
答案
1.C 解析:
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠BAD=90°,OA=OB=OC=OD,AC⊥BD,
∴△ABC,△ADC,△ABD,△BCD,△AOB,△BOC,△AOD,△COD都是等腰直角三角形.
故选C.
2.B 解析:
A.只有矩形、正方形的对角线相等,故本选项错误;B.平行四边形、矩形、菱形、正方形的对角线都互相平分,故本选项正确;C.只有菱形、正方形的对角线互相垂直,故本选项错误;D.只有菱形、正方形的对角线互相垂直平分,故本选项错误.故选B.
3.A 解析:
∵正方形的一条对角线长为4,
∴这个正方形的面积=×4×4=8.故选A.
4.C 解析:
∵四边形ABCD是正方形,
∴∠DBC=45°.
∵BP=BC,∴∠BCP=∠BPC=(180°-45°)=67.5°.
5.证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠C=90°.
在△ABE和△BCF中,
∴△ABE≌△BCF.
(2)如图,设AE与BF交于点O.
∵△ABE≌△BCF,
∴∠BAE=∠CBF.
∵∠ABE=90°,∴∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,
∴∠BOE=90°,即AE⊥BF.
6.D 解析:
A错误,四边相等的四边形是菱形.B错误,四角相等的四边形是矩形.C错误,对角线互相垂直的平行四边形是菱形.D正确,对角线互相垂直平分且相等的四边形是正方形.故选D.
7.B 解析:
添加①可得平行四边形ABCD是菱形,添加②可得平行四边形ABCD是矩形,添加③可得平行四边形ABCD是矩形,添加④可得平行四边形ABCD是菱形,所以选②③不能使得平行四边形ABCD是正方形.
8.∠ABC=90°(答案不唯一)
9.证明:(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC边的中点,∴BD=CD,
∴△BED≌△CFD.
(2)∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
又∵∠A=90°,∴四边形DFAE是矩形.
∵△BED≌△CFD,
∴DE=DF,∴矩形DFAE是正方形.
10.
11.2
12.(-3,1) 解析:
如图,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,则∠OAD+∠AOD=90°.
∵四边形OABC是正方形,
∴OA=CO,∠AOC=90°,
∴∠COE+∠AOD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,
∴△AOD≌△OCE(AAS),
∴OE=AD=3,CE=OD=1.
∵点C在第二象限,
∴点C的坐标为(-3,1).
故答案为(-3,1).
13.解:(1)证明:∵四边形ABCD为正方形,
∴AB=AD=DC=BC,∠D=∠B=90°.
∵E,F分别为DC,BC的中点,
∴DE=DC,BF=BC,∴DE=BF.
在△ADE和△ABF中,
∴△ADE≌△ABF(SAS).
(2)由题意知AB=AD=4,
DE=BF=CE=CF=×4=2,
∴S△AEF=S正方形ABCD-S△ABF-S△ADE-S△CEF=4×4-×4×2-×4×2-×2×2=6.
14.证明:(1)∵BD平分∠ABC,
∴∠ABD=∠CBD.
又∵AB=CB,BD=BD,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB.
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°.
又∵∠ADC=90°,
∴四边形MPND是矩形.
∵∠ADB=∠CDB,PM⊥AD,PN⊥CD,
∴PM=PN,
∴四边形MPND是正方形.
15.解:(1)证明:∵四边形ABCD是矩形,AB=BC,
∴四边形ABCD是正方形,∠ADC=90°,
∴AD=DC,∠CDE+∠ADF=90°.
∵CE⊥DG,AF∥CE,
∴∠CED=∠CEF=∠DFA=90°.
∵∠DAF+∠ADF=90°,
∴∠CDE=∠DAF,
∴△AFD≌△DEC(AAS),∴AF=DE,
∴DF-AF=DF-DE=EF.
(2)延长DG,CB相交于点H,如图.
∵四边形ABCD是矩形,AB=BC,
∴四边形ABCD是正方形,
∴AD=AB=BC.
∵G是AB的中点,
∴AG=BG,
∴=.
在△ADG和△BHG中,
∴△ADG≌△BHG(ASA),
∴AD=BH.
∵AD=BC,
∴BH=BC,
即B是CH的中点.
∵CE⊥DG,∴∠CEH=90°,
即△CEH是直角三角形,
∴BE=CH=BC,∴BE=AB,
∴==.
