人教版七年级数学 下册 第九章 9.3 一元一次不等式组 课件(共45张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第九章 9.3 一元一次不等式组 课件(共45张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 20:58:16 | ||
图片预览











文档简介
(共45张PPT)
温故知新
1.什么是一元一次不等式?
2.什么是一元一次不等式的解?
3.解一元一次不等式的基本步骤?
解一元一次不等式的基本步骤
1、去分母
(不等式的性质2)
2、去括号
(乘法分配律)
3、移项
(不等式的性质1)
4、合并同类项
(整式加减性质)
5、化系数为1
(不等式性质2,3)
温故知新
同学们,你能根据上图对话片断估计出这头大象的体重范围吗?请说说你的理由!
看,这头大象好大呀,体重肯定不少于3吨!
嗨,我听管理员说,这头大象的体重不足5吨呢!
若设大象的体重为x吨,请用不等式的知识分别表示上
面两位同学所谈话的内容:
导入新课
9.3
一元一次不等式组
人教版七年级数学
下册
目标导航
1.掌握一元一次不等式组概念及解法。
2.形成正确的解不等式组的思路与方法;(重点、难点)
3.掌握在数轴上正确表示一元一次不等式组的解集的方法。
认真阅读课本中9.1.2
不等式的性质的内容,完成下面练习并体验知识点的形成过程。
自主研学
我们可以这样读书:
点信息,划精要
,圈疑问
一边读一边做标识,
一边读一边做评注,
一边读一边做概括.
目标导航一
一元一次不等式组
情境引入
我90千克
我x千克
我40千克
嗨嗨,你知道小猪大约有多重?
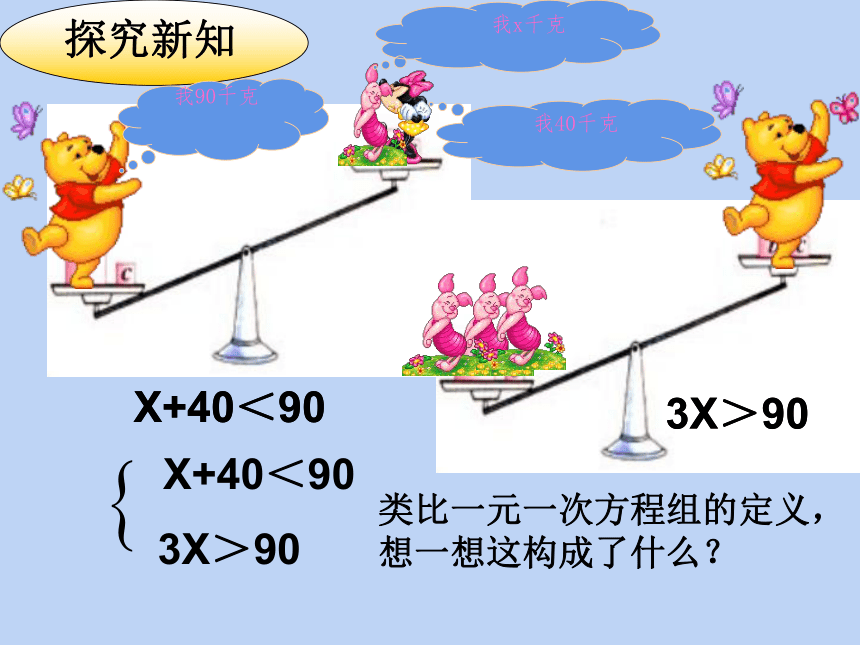
探究新知
我90千克
我x千克
我40千克
X+40<90
3X>90
X+40<90
3X>90
类比一元一次方程组的定义,想一想这构成了什么?
X+40<90
3X>90
我们用大括号把上述两个不等式联立起来,得
像
这样,关于同一未知数的两个一元一次不等式合在一起,就组成一个一元一次不等式组.
对概念的理解:
1、几个指两个或两个以上;
2、只有一个未知数;
3、由一元一次不等式组成.
各式中,哪些是一元一次不等式组?
√
×
√
×
×
√
即学即练
思考:怎样确定上面的不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
归纳:我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
目标导航二
一元一次不等式组的解法
如何解此不等式组的解集呢?
分析
类比方程组的解,怎样确定
不等式组中X的取值范围呢?
不等式组中的各不等式解集的公共部分,
就是不等式组中X的取值范围
大于向右画,小于向左画;
有等号的画实心圆点,无等号的画空心圆圈.
知识回顾
在数轴上表示不等式的解集时应注意:
②
①
动手操作:
-2
-1 0 1 2 3 4 5 6
一般地,几个一元一次不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.求一元一次不等式组解集的过程叫做解不等式组.
运用数轴,把不等式组中两个不等式的解集分别在同一数轴上表示出来,并找出其公共部分.
结论:
。
。
合作探究
2
1
3
0
不等式组的解集为
同大取大
利用数轴求下列不等式的解集。
合作探究
2
1
3
0
不等式组的解集为
同小取小
2
1
3
0
不等式组的解集为
大小,小大中间找
2
1
3
0
两个不等式的解集没有公共部分,
即:不等式组无解
大大,小小解没了
a
a
a
b
x>a
x>
b
x<a
x<b
x<a
x>
b
x>a
x<b
。
。
a
。
。
b
。
。
b
。
。
b
解集为
:
x>
b
(同大取大)
解集为
:
x<a
(同小取小)
一元一次不等式组的解集的规律图析
(若当
a<b时
)
解集为:
a<x<b
(大小相对取中间)
解集为:无解
(大小相背则无解)
解不等式②,得
x
<-3.
例1
解不等式组:
解:
解不等式①,得
x
≤
3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是
x<-3,所以这个不等式组的解集是
x<-3.
精典例题
解一元一次不等式组的一般步骤:
分别求出各个不等式的解集
在数轴上表示出各个不等式的解集
找公共部分
用不等式表示出解集
知识归纳
2x-1>x+1
x+8<4x-1
例2:解不等式组
①
②
解:
由不等式①
x>
2.
由不等式②
x>
3.
∴原不等式组的解集是
x>3
把不等式①和
②的解集在数轴上表示:
2
3
0
1
精典例题
例3
解不等式组:
解
解不等式①,得
x
<-2.
解不等式②,得
x
>3.
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
由图可以看出这两个不等式的解集没有公共部分.所以,这个不等式组无解.
0
-2
3
例4
已知不等式组
的解集为-1<x<1,
则(a+1)(b-1)的值为多少?
2x—a<1
x—2b>3
解:
由不等式组得:
x
<
x
>3+2b
因为不等式组的解集为:
-1<
x
<
1
,
所以,
=1
3+2b=
-1
解得
a=1
,
b=
-
2
所以(a+1)(b-1)=2×(-3)=-6
求不等式组解集的规律:
1.
同大取大,
2.同小取小;
3.大小小大取中间;
4.大大小小取无解。
巧记口诀
不等式组
的解集在数轴上表示为(
)
≥-2,
-5
-2
-5
-2
-5
-2
-5
-2
A.
D.
C.
B.
B
即学即练
目标导航三
一元一次不等式组应用
例5.
3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
精典例题
解:设每个小组原先每天生产x件产品,由题意,得
3×10x<500,
3×10(x+1)>500
解不等式组,得
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
列一元一次不等式组解实际问题的一般步骤:
(1)审题;
(2)设未知数,找不等量关系;
(3)根据不等关系列不等式组;
(4)解不等式组;
(5)检验并作答.
方法归纳
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例6
用若干辆载重量为
8
t
的汽车运一批货物,若每辆汽车只装
4
t
,则剩下
20
t
货物;若每辆汽车装满
8
t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x
辆汽车,则这批货物共有(4x+20
)t.依题意得
解不等式组,得5<x
<7.
精典例题
一元一次不等式组概念:
两个含相同未知数的一元一次不等式合在一起,就得到一个.
一元一次不等式组的解集
不等式组中几个不等式的解集的公共部分
同大取大;
同小取小;
交叉解集中间找;
两头去,无解了。
一元一次不等式解集寻找口诀:
{
一元一次不等式组
课堂小结
感受数学思想
1、与方程组的类比引入不等式组。
2、利用数轴直观地表示不等式组的解集。
类比思想
数形结合思想
课堂小结
1.关于x的不等式组
的解集为x>3,则a的取值范围是( )。
A、a≥-3
B、a≤-3
C、a>-3
D、a<-3
A
检测目标
2.不等式组
的解集是(
)
≥2,
≤2
A.
≥2,
D.
=2.
B.
≤2,
C.
无解,
D
检测目标
C
3.不等式组
的整数解是(
)
D.
≤1.
A.
0,
1
,
B.
0
,
C.
1,
≤1
检测目标
4.不等式组
的解集在数轴上
表示为(
)
(A)
(B)
(C)
(D)
【解析】选C.
解不等式①得x>1,解不等式
②得:x≥2,表示在数轴上为C选项.
②
①
检测目标
C
5.如图,
则其解集是(
)
-1
2.5
4
B
A.
B.
C.
D.
≤4
≤4,
检测目标
7、若不等式组
的解集是-1<x<2,则m=____, n=____.
①
②
解:
解不等式①,得,x>m-2
解不等式②,得,x
<
n
+
1
因为不等式组有解,所以
m-2
<x<
n
+
1
又因为 -1<x<2
所以,m=1
, n=1
-1
2
< x <
m-2
n
+
1
m-2=
-1 , n
+
1
=
2
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
温故知新
1.什么是一元一次不等式?
2.什么是一元一次不等式的解?
3.解一元一次不等式的基本步骤?
解一元一次不等式的基本步骤
1、去分母
(不等式的性质2)
2、去括号
(乘法分配律)
3、移项
(不等式的性质1)
4、合并同类项
(整式加减性质)
5、化系数为1
(不等式性质2,3)
温故知新
同学们,你能根据上图对话片断估计出这头大象的体重范围吗?请说说你的理由!
看,这头大象好大呀,体重肯定不少于3吨!
嗨,我听管理员说,这头大象的体重不足5吨呢!
若设大象的体重为x吨,请用不等式的知识分别表示上
面两位同学所谈话的内容:
导入新课
9.3
一元一次不等式组
人教版七年级数学
下册
目标导航
1.掌握一元一次不等式组概念及解法。
2.形成正确的解不等式组的思路与方法;(重点、难点)
3.掌握在数轴上正确表示一元一次不等式组的解集的方法。
认真阅读课本中9.1.2
不等式的性质的内容,完成下面练习并体验知识点的形成过程。
自主研学
我们可以这样读书:
点信息,划精要
,圈疑问
一边读一边做标识,
一边读一边做评注,
一边读一边做概括.
目标导航一
一元一次不等式组
情境引入
我90千克
我x千克
我40千克
嗨嗨,你知道小猪大约有多重?
探究新知
我90千克
我x千克
我40千克
X+40<90
3X>90
X+40<90
3X>90
类比一元一次方程组的定义,想一想这构成了什么?
X+40<90
3X>90
我们用大括号把上述两个不等式联立起来,得
像
这样,关于同一未知数的两个一元一次不等式合在一起,就组成一个一元一次不等式组.
对概念的理解:
1、几个指两个或两个以上;
2、只有一个未知数;
3、由一元一次不等式组成.
各式中,哪些是一元一次不等式组?
√
×
√
×
×
√
即学即练
思考:怎样确定上面的不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
归纳:我们把几个一元一次不等式解集的公共部分,叫作由它们所组成的一元一次不等式组的解集.
求不等式组的解集的过程,叫作解不等式组.
目标导航二
一元一次不等式组的解法
如何解此不等式组的解集呢?
分析
类比方程组的解,怎样确定
不等式组中X的取值范围呢?
不等式组中的各不等式解集的公共部分,
就是不等式组中X的取值范围
大于向右画,小于向左画;
有等号的画实心圆点,无等号的画空心圆圈.
知识回顾
在数轴上表示不等式的解集时应注意:
②
①
动手操作:
-2
-1 0 1 2 3 4 5 6
一般地,几个一元一次不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.求一元一次不等式组解集的过程叫做解不等式组.
运用数轴,把不等式组中两个不等式的解集分别在同一数轴上表示出来,并找出其公共部分.
结论:
。
。
合作探究
2
1
3
0
不等式组的解集为
同大取大
利用数轴求下列不等式的解集。
合作探究
2
1
3
0
不等式组的解集为
同小取小
2
1
3
0
不等式组的解集为
大小,小大中间找
2
1
3
0
两个不等式的解集没有公共部分,
即:不等式组无解
大大,小小解没了
a
a
a
b
x>a
x>
b
x<a
x<b
x<a
x>
b
x>a
x<b
。
。
a
。
。
b
。
。
b
。
。
b
解集为
:
x>
b
(同大取大)
解集为
:
x<a
(同小取小)
一元一次不等式组的解集的规律图析
(若当
a<b时
)
解集为:
a<x<b
(大小相对取中间)
解集为:无解
(大小相背则无解)
解不等式②,得
x
<-3.
例1
解不等式组:
解:
解不等式①,得
x
≤
3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是
x<-3,所以这个不等式组的解集是
x<-3.
精典例题
解一元一次不等式组的一般步骤:
分别求出各个不等式的解集
在数轴上表示出各个不等式的解集
找公共部分
用不等式表示出解集
知识归纳
2x-1>x+1
x+8<4x-1
例2:解不等式组
①
②
解:
由不等式①
x>
2.
由不等式②
x>
3.
∴原不等式组的解集是
x>3
把不等式①和
②的解集在数轴上表示:
2
3
0
1
精典例题
例3
解不等式组:
解
解不等式①,得
x
<-2.
解不等式②,得
x
>3.
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
由图可以看出这两个不等式的解集没有公共部分.所以,这个不等式组无解.
0
-2
3
例4
已知不等式组
的解集为-1<x<1,
则(a+1)(b-1)的值为多少?
2x—a<1
x—2b>3
解:
由不等式组得:
x
<
x
>3+2b
因为不等式组的解集为:
-1<
x
<
1
,
所以,
=1
3+2b=
-1
解得
a=1
,
b=
-
2
所以(a+1)(b-1)=2×(-3)=-6
求不等式组解集的规律:
1.
同大取大,
2.同小取小;
3.大小小大取中间;
4.大大小小取无解。
巧记口诀
不等式组
的解集在数轴上表示为(
)
≥-2,
-5
-2
-5
-2
-5
-2
-5
-2
A.
D.
C.
B.
B
即学即练
目标导航三
一元一次不等式组应用
例5.
3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
精典例题
解:设每个小组原先每天生产x件产品,由题意,得
3×10x<500,
3×10(x+1)>500
解不等式组,得
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
列一元一次不等式组解实际问题的一般步骤:
(1)审题;
(2)设未知数,找不等量关系;
(3)根据不等关系列不等式组;
(4)解不等式组;
(5)检验并作答.
方法归纳
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例6
用若干辆载重量为
8
t
的汽车运一批货物,若每辆汽车只装
4
t
,则剩下
20
t
货物;若每辆汽车装满
8
t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x
辆汽车,则这批货物共有(4x+20
)t.依题意得
解不等式组,得5<x
<7.
精典例题
一元一次不等式组概念:
两个含相同未知数的一元一次不等式合在一起,就得到一个.
一元一次不等式组的解集
不等式组中几个不等式的解集的公共部分
同大取大;
同小取小;
交叉解集中间找;
两头去,无解了。
一元一次不等式解集寻找口诀:
{
一元一次不等式组
课堂小结
感受数学思想
1、与方程组的类比引入不等式组。
2、利用数轴直观地表示不等式组的解集。
类比思想
数形结合思想
课堂小结
1.关于x的不等式组
的解集为x>3,则a的取值范围是( )。
A、a≥-3
B、a≤-3
C、a>-3
D、a<-3
A
检测目标
2.不等式组
的解集是(
)
≥2,
≤2
A.
≥2,
D.
=2.
B.
≤2,
C.
无解,
D
检测目标
C
3.不等式组
的整数解是(
)
D.
≤1.
A.
0,
1
,
B.
0
,
C.
1,
≤1
检测目标
4.不等式组
的解集在数轴上
表示为(
)
(A)
(B)
(C)
(D)
【解析】选C.
解不等式①得x>1,解不等式
②得:x≥2,表示在数轴上为C选项.
②
①
检测目标
C
5.如图,
则其解集是(
)
-1
2.5
4
B
A.
B.
C.
D.
≤4
≤4,
检测目标
7、若不等式组
的解集是-1<x<2,则m=____, n=____.
①
②
解:
解不等式①,得,x>m-2
解不等式②,得,x
<
n
+
1
因为不等式组有解,所以
m-2
<x<
n
+
1
又因为 -1<x<2
所以,m=1
, n=1
-1
2
< x <
m-2
n
+
1
m-2=
-1 , n
+
1
=
2
检测目标
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
