苏科新版七年级数学下册第7章平面图形的认识(二)同步检测卷(Word版 含解析)
文档属性
| 名称 | 苏科新版七年级数学下册第7章平面图形的认识(二)同步检测卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 231.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-04 22:59:22 | ||
图片预览



文档简介
苏科新版七年级数学下册第7章平面图形的认识(二)同步检测卷
满分120分
班级: 姓名: 得分:
一.选择题(共12小题,满分36分)
1.下列长度的三条线段能组成三角形的是( )
A.4,5,9 B.5,5,11 C.5,6,10 D.1,2,3
2.观察下面四幅图案中,能通过如图图案平移得到的是( )
A.B.C.D.
3.下列条件中,可能得到平行线的是( )
A.对顶角的角平分线 B.邻补角的角平分线
C.同位角的角平分线 D.同旁内角的角平分线
4.如图所示,△ABC的边AC上的高是( )
A.线段AE B.线段BA C.线段BD D.线段DA
5.如果过一个多边形的一个顶点的对角线有6条,则该多边形对角线一共有( )
A.18条 B.14条 C.20条 D.27条
6.如图,已知直线a∥b∥c,直线d与它们分别垂直且相交于A,B,C三点,若AB=2,AC=6,则平行线b、c之间的距离是( )
A.2 B.4 C.6 D.8
7.如图,给出下列四个条件:①AC=BD;②∠DAC=∠BCA;③∠ABD=∠CDB;④∠ADB=∠CBD,其中能使AD∥BC的条件为( )
A.①② B.③④ C.②④ D.①③④
8.如图,直线a∥b,将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为( )
A.20° B.30° C.40° D.50°
9.直角三角板和直尺如图放置,若∠1=30°,则∠2的度数为( )
A.60° B.50° C.40° D.30°
10.一个多边形的内角和比它的外角和的2倍少180°,这个多边形的边数是( )
A.5 B.6 C.7 D.8
11.如图,CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E,∠B=35°,∠E=25°,则∠ACD的度数为( )
A.100° B.110° C.120° D.130°
12.若AB∥CD,∠CDF=∠CDE,∠ABF=∠ABE,过E、F分别作EM∥AB,FN∥AB,则∠E:∠F=( )
A.2:1 B.3:1 C.4:3 D.3:2
二.填空题(共7小题,满分28分)
13.如图,为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的 性.
14.如图所示,图中的同位角有 对.
15.已知正n边形的每个内角为144°,则n= .
16.如图,将△ABC沿着射线BC的方向平移,得到△DEF,若EF=13,EC=7,则平移的距离为 .
17.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为 度.
18.如图,在△ABC中,BD平分∠ABC,连接CD,若∠A=∠D=40°,∠ACD=30°,则∠DCE的度数为 .
19.平移小平行四边形◇可以得到美丽的“中国结”图案,下面四个图案是由◇平移后得到的类似“中国结”的图案,按图中规律,第18个图案中,小平行四边形的个数是 个.
三.解答题(共7小题,满分56分)
20.(6分)如图,已知∠COF+∠C=180°,∠C=∠B.说明AB∥EF的理由.
21.(7分)如图,在△ABC中,AD是高,角平分线AE,BF相交于点O,∠BAC=50°,∠C=70°,求∠DAC和∠BOA的大小.
22.(7分)如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
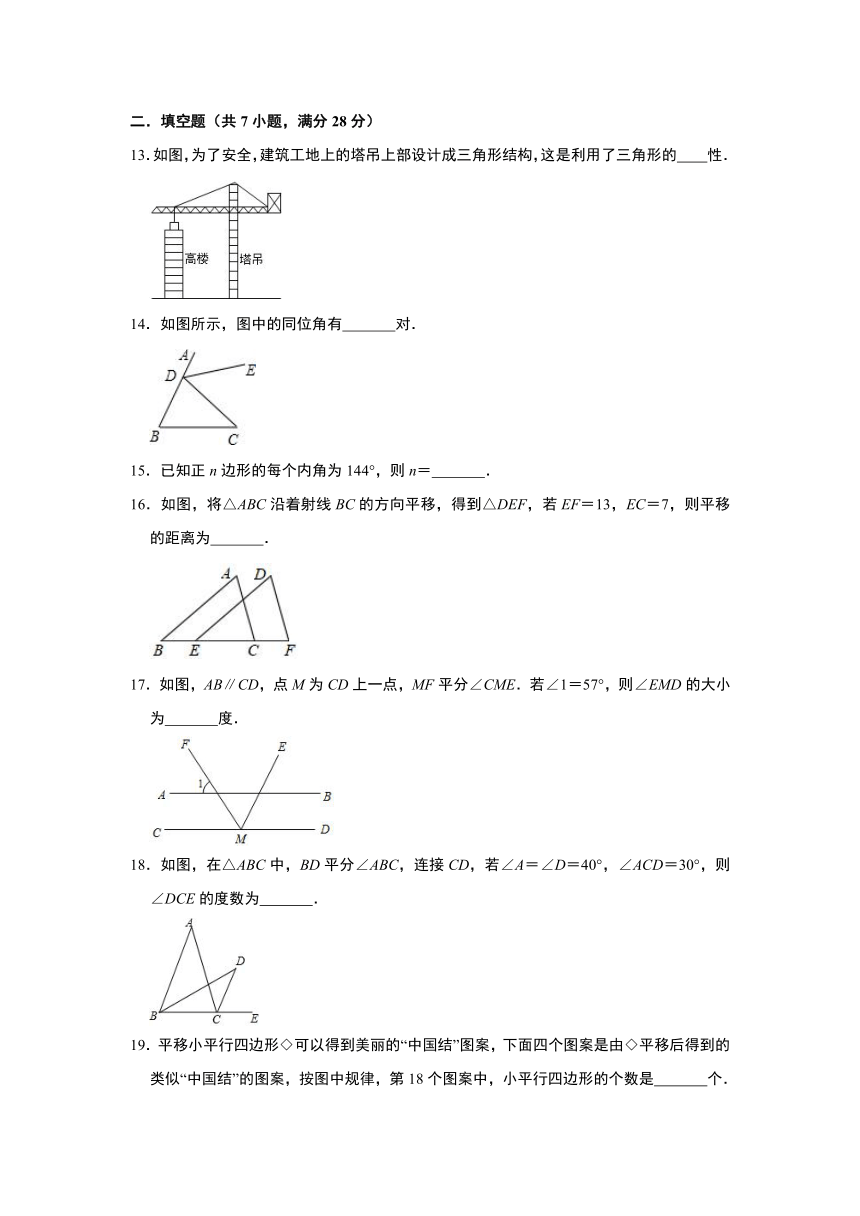
23.(8分)如图,已知AB∥CD,E是直线AB上的一点,CE平分∠ACD,射线CF⊥CE,∠1=32°,
(1)求∠ACE的度数;
(2)若∠2=58°,求证:CF∥AG.
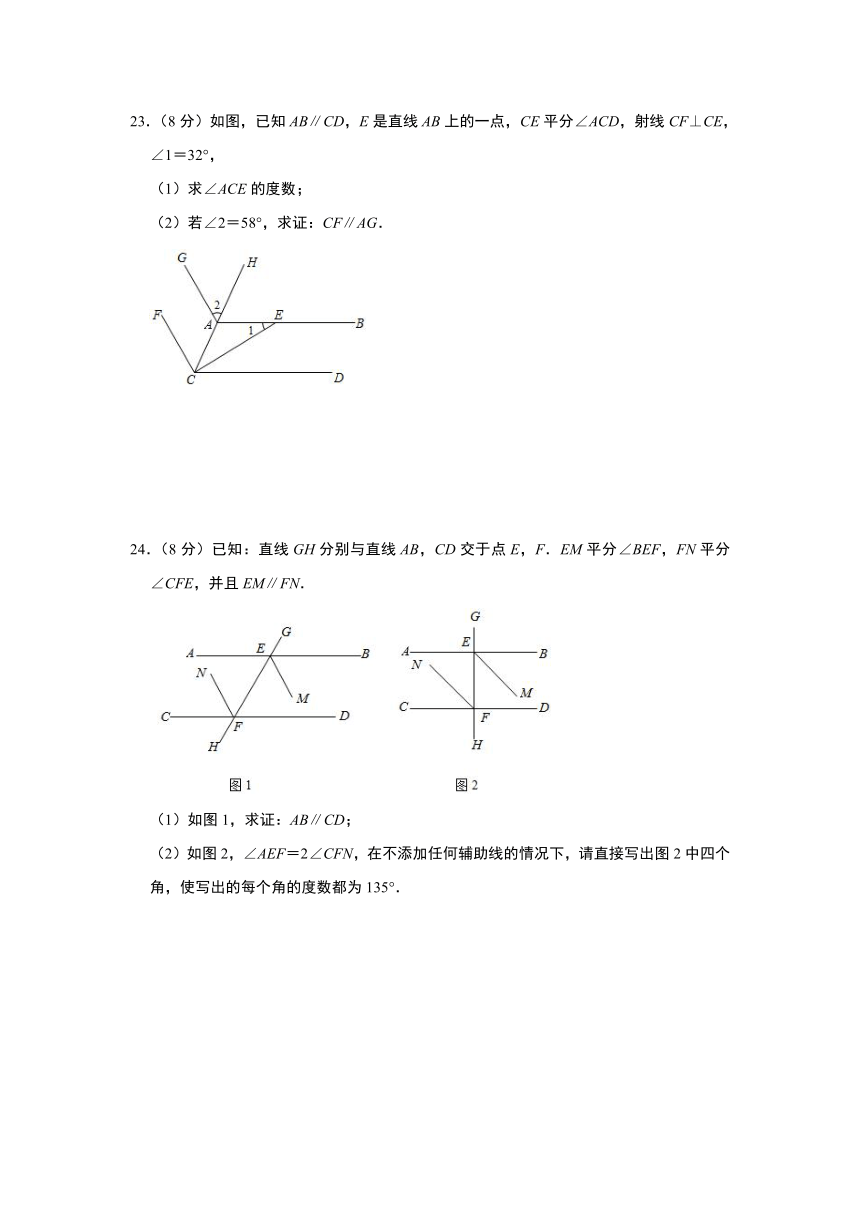
24.(8分)已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
25.(10分)(1)如图1,则∠A、∠B、∠C、∠D之间的数量关系为 .
(2)如图2,AP、CP分别平分∠BAD、∠BCD.若∠B=36°,∠D=14°,求∠P的度数;
(3)如图3,CP、AG分别平分∠BCE、∠FAD,AG反向延长线交CP于点P,请猜想∠P、∠B、∠D之间的数量关系.并说明理由.
26.(10分)如图1,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
(1)若∠MON=60°,则∠ACG= ;(直接写出答案)
(2)若∠MON=n°,求出∠ACG的度数;(用含n的代数式表示)
(3)如图2,若∠MON=80°,过点C作CF∥OA交AB于点F,求∠BGO与∠ACF的数量关系.
参考答案
一.选择题(共12小题,满分36分)
1.【解答】解:根据三角形的三边关系,
A、5+4=9,不能组成三角形,不符合题意;
B、5+5=10<11,不能够组成三角形,不符合题意;
C、5+6=11>10,能组成三角形,符合题意;
D、1+2=3,不能组成三角形,不符合题意.
故选:C.
2.【解答】解:能通过如图图案平移得到的是B.
故选:B.
3.【解答】解:A、对顶角的角平分线AC、AD共线,
故错误;
B、∵,,
∠PAM+∠MAB=180°,
∴∠CAM+∠MAE=90°,
∴邻补角的角平分线相互垂直,
故错误;
C、同位角的角平分线AC、BF互相平行,
∵AM∥BN,∴∠PAM=∠PBN;
∵AC、BF是∠PAM和∠PBN的角平分线,
∴∠1=∠PAM=∠PBN=∠2;
∴AC∥BF.故正确.
D、同旁内角的角平分线AE、BF互相垂直,
∵AM∥BN,∴∠MAB+∠PBN=180°;
∵AE、BF是∠MAB和∠PBN的角平分线,
∴∠3+∠2=∠MAB+∠PBN=90°;
∴AE⊥BF.故错误.
故选:C.
4.【解答】解:由题意可知,△ABC的边AC上的高是线段BD.
故选:C.
5.【解答】解:∵过一个多边形的一个顶点的对角线有6条,
∴多边形的边数为6+3=9,
∴这个多边形是九边形.
∴该多边形对角线一共有:=27(条).
故选:D.
6.【解答】解:∵直线a∥b∥c,直线d与它们分别垂直且相交于A,B,C三点,
∴AB长为直线a和b之间的距离,BC长为直线b和c之间的距离,AC长为直线a和c之间的距离,
又∵AB=2,AC=6,
∴BC=6﹣2=4,
即平行线b、c之间的距离是4.
故选:B.
7.【解答】解:②由∠DAC=∠BCA可得AD∥BC,
④由∠ADB=∠CBD可得AD∥BC,
故选:C.
8.【解答】解:∵直线a∥b,
∴∠1+∠BCA+∠2+∠BAC=180°,
∵∠BAC=30°,∠BCA=90°,∠1=20°,
∴∠2=40°.
故选:C.
9.【解答】解:如图,过E作EF∥AB,
则AB∥EF∥CD,
∴∠3=∠1,∠2=∠4,
∵∠3+∠4=60°,
∴∠1+∠2=60°,
∵∠1=30°,
∴∠2=30°,
故选:D.
10.【解答】解:设这个多边形为n边形,由题意得,
(n﹣2)×180°=360°×2﹣180°,
解得n=5,
即这个多边形为五边形,
故选:A.
11.【解答】解:∵∠ECD是△BCE的一个外角,
∴∠ECD=∠B+∠E=35°+25°=60°,
∵CE平分∠ACD,
∴∠ACD=2∠ECD=120°,
故选:C.
12.【解答】解:过E、F分别作EM∥AB,FN∥AB,
∵AB∥CD,
∴CD∥EM,CD∥FN,
∴∠CDE=∠DEM,∠ABE=∠BEM,∠CDF=∠DFN,∠ABF=∠BFN,
∴∠DEB=∠CDE+∠ABE,∠DFB=∠CDF+∠ABF,
∵∠CDF=∠CDE,∠ABF=∠ABE
∴∠DFB=∠CDE+∠ABE=∠DEB,
∴∠DEB:∠DFB=3:2,
故选:D.
二.填空题(共7小题,满分28分)
13.【解答】解:为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的稳定性,
故答案为:稳定.
14.【解答】解:DE、BC被AB所截,∠ADE与∠B是同位角;
DC、BC被AB所截,∠ADC与∠B是同位角.
故图中有两对同位角.
15.【解答】解:由题意得正n边形的每一个外角为180°﹣144°=36°,
n=360°÷36°=10,
故答案为10.
16.【解答】解:∵△ABC沿着射线BC的方向平移,得到△DEF,
∴BE=CF,
∵EF=13,EC=7,
∴BE+7+CF=13,
即2BE+7=13,解得BE=3,
即平移的距离为3.
故答案为3.
17.【解答】解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
18.【解答】解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠ACE=∠A+∠ABC=40°+2∠CBD,
∴∠DCE+∠ACD=∠A+2∠CBD,
∵∠DCE=∠CBD+∠D,∠A=∠D=40°,∠ACD=30°,
∴∠DCE+30°=40°+2∠CBD,即∠DCE=2∠CBD+10°①,
∠DCE=40°+∠CBD②,
由①②得∠DCE=70°,
故答案为:70°.
19.【解答】解:第一个图形有2×12=2个小平行四边形,
第二个图形有2×22=8个小平行四边形,
第三个图形有2×32=18个小平行四边形,
…
第n个图形有2n2个小平行四边形,
第18个图形有2×182=648个小平行四边形.
故答案为:648.
三.解答题(共7小题,满分56分)
20.【解答】解:∵∠COF+∠C=180°,
∴EF∥CD,
∵∠C=∠B,
∴AB∥CD,
∴AB∥EF.
21.【解答】解:∵AD是△ABC的高线,
∴∠ADC=90°,
∵∠ADC+∠C+∠CAD=180°,∠C=70°,
∴∠CAD=180°﹣90°﹣70°=20°;
∵∠ABC+∠C+∠CAB=180°,∠C=70°,∠BAC=50°,
∴∠ABC=180°﹣70°﹣50°=60°,
∵AE,BF分别平分∠BAC,∠ABC,AE,BF相交于点O,
∴∠BAO=∠BAC=25°,∠ABO=∠ABC=30°,
∵∠ABO+∠BAO+∠AOB=180°,
∴∠AOB=180°﹣25°﹣30°=125°.
22.【解答】解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
23.【解答】解:(1)∵AB∥CD,
∴∠1=∠DCE=32°,
∵CE平分∠ACD,
∴∠ACE=∠DCE=32°;
(2)∵CF⊥CE,
∴∠FCE=90°,
∴∠FCH=90°﹣32°=58°,
∵∠2=58°,
∴∠FCH=∠2,
∴CF∥AG.
24.【解答】(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
25.【解答】解:(1)∵∠AOB+∠A+∠B=∠COD+∠C+∠D=180°,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D,
故答案为∠A+∠B=∠C+∠D;
(2)∵AP、CP分别平分∠BAD、∠BCD,
∴∠BAP=∠DAP,∠BCP=∠DCP,
由(1)可得:∠BAP+∠B=∠BCP+∠P,∠DAP+∠P=∠DCP+∠D,
∴∠B﹣∠P=∠P﹣∠D,
即2∠P=∠B+∠D,
∵∠B=36°,∠D=14°,
∴∠P=25°;
(3)2∠P=∠B+∠D.
理由:∵CP、AG分别平分∠BCE、∠FAD,
∴∠ECP=∠PCB,∠FAG=∠GAD,
∵∠PAB=∠FAG,
∴∠GAD=∠PAB,
∵∠P+∠PAB=∠B+∠PCB,
∴∠P+∠GAD=∠B+∠PCB,
∵∠P+∠PAD=∠D+∠PCD,
∴∠P+(180°﹣∠GAD)=∠D+(180°﹣∠ECP),
∴2∠P=∠B+∠D.
26.【解答】解:(1)∵∠MON=60°,
∴∠BAO+∠ABO=120°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=60°,
∴∠ACG=∠CBA+∠CAB=60°,
故答案为:60°;
(2)∵∠MON=n°,
∴∠BAO+∠ABO=180°﹣n°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=90°﹣n°,
∴∠ACG=∠CBA+∠CAB=90°﹣n°;
(3)∵CF∥OA,
∴∠ACF=∠CAG,
∴∠BGO﹣∠ACF=∠BGO﹣∠CAG=∠ACG=90°﹣80°=50°.
满分120分
班级: 姓名: 得分:
一.选择题(共12小题,满分36分)
1.下列长度的三条线段能组成三角形的是( )
A.4,5,9 B.5,5,11 C.5,6,10 D.1,2,3
2.观察下面四幅图案中,能通过如图图案平移得到的是( )
A.B.C.D.
3.下列条件中,可能得到平行线的是( )
A.对顶角的角平分线 B.邻补角的角平分线
C.同位角的角平分线 D.同旁内角的角平分线
4.如图所示,△ABC的边AC上的高是( )
A.线段AE B.线段BA C.线段BD D.线段DA
5.如果过一个多边形的一个顶点的对角线有6条,则该多边形对角线一共有( )
A.18条 B.14条 C.20条 D.27条
6.如图,已知直线a∥b∥c,直线d与它们分别垂直且相交于A,B,C三点,若AB=2,AC=6,则平行线b、c之间的距离是( )
A.2 B.4 C.6 D.8
7.如图,给出下列四个条件:①AC=BD;②∠DAC=∠BCA;③∠ABD=∠CDB;④∠ADB=∠CBD,其中能使AD∥BC的条件为( )
A.①② B.③④ C.②④ D.①③④
8.如图,直线a∥b,将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为( )
A.20° B.30° C.40° D.50°
9.直角三角板和直尺如图放置,若∠1=30°,则∠2的度数为( )
A.60° B.50° C.40° D.30°
10.一个多边形的内角和比它的外角和的2倍少180°,这个多边形的边数是( )
A.5 B.6 C.7 D.8
11.如图,CE是△ABC的外角∠ACD的平分线,CE交BA的延长线于点E,∠B=35°,∠E=25°,则∠ACD的度数为( )
A.100° B.110° C.120° D.130°
12.若AB∥CD,∠CDF=∠CDE,∠ABF=∠ABE,过E、F分别作EM∥AB,FN∥AB,则∠E:∠F=( )
A.2:1 B.3:1 C.4:3 D.3:2
二.填空题(共7小题,满分28分)
13.如图,为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的 性.
14.如图所示,图中的同位角有 对.
15.已知正n边形的每个内角为144°,则n= .
16.如图,将△ABC沿着射线BC的方向平移,得到△DEF,若EF=13,EC=7,则平移的距离为 .
17.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为 度.
18.如图,在△ABC中,BD平分∠ABC,连接CD,若∠A=∠D=40°,∠ACD=30°,则∠DCE的度数为 .
19.平移小平行四边形◇可以得到美丽的“中国结”图案,下面四个图案是由◇平移后得到的类似“中国结”的图案,按图中规律,第18个图案中,小平行四边形的个数是 个.
三.解答题(共7小题,满分56分)
20.(6分)如图,已知∠COF+∠C=180°,∠C=∠B.说明AB∥EF的理由.
21.(7分)如图,在△ABC中,AD是高,角平分线AE,BF相交于点O,∠BAC=50°,∠C=70°,求∠DAC和∠BOA的大小.
22.(7分)如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
23.(8分)如图,已知AB∥CD,E是直线AB上的一点,CE平分∠ACD,射线CF⊥CE,∠1=32°,
(1)求∠ACE的度数;
(2)若∠2=58°,求证:CF∥AG.
24.(8分)已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
25.(10分)(1)如图1,则∠A、∠B、∠C、∠D之间的数量关系为 .
(2)如图2,AP、CP分别平分∠BAD、∠BCD.若∠B=36°,∠D=14°,求∠P的度数;
(3)如图3,CP、AG分别平分∠BCE、∠FAD,AG反向延长线交CP于点P,请猜想∠P、∠B、∠D之间的数量关系.并说明理由.
26.(10分)如图1,点A、B分别在射线OM、ON上运动(不与点O重合),AC、BC分别是∠BAO和∠ABO的角平分线,BC延长线交OM于点G.
(1)若∠MON=60°,则∠ACG= ;(直接写出答案)
(2)若∠MON=n°,求出∠ACG的度数;(用含n的代数式表示)
(3)如图2,若∠MON=80°,过点C作CF∥OA交AB于点F,求∠BGO与∠ACF的数量关系.
参考答案
一.选择题(共12小题,满分36分)
1.【解答】解:根据三角形的三边关系,
A、5+4=9,不能组成三角形,不符合题意;
B、5+5=10<11,不能够组成三角形,不符合题意;
C、5+6=11>10,能组成三角形,符合题意;
D、1+2=3,不能组成三角形,不符合题意.
故选:C.
2.【解答】解:能通过如图图案平移得到的是B.
故选:B.
3.【解答】解:A、对顶角的角平分线AC、AD共线,
故错误;
B、∵,,
∠PAM+∠MAB=180°,
∴∠CAM+∠MAE=90°,
∴邻补角的角平分线相互垂直,
故错误;
C、同位角的角平分线AC、BF互相平行,
∵AM∥BN,∴∠PAM=∠PBN;
∵AC、BF是∠PAM和∠PBN的角平分线,
∴∠1=∠PAM=∠PBN=∠2;
∴AC∥BF.故正确.
D、同旁内角的角平分线AE、BF互相垂直,
∵AM∥BN,∴∠MAB+∠PBN=180°;
∵AE、BF是∠MAB和∠PBN的角平分线,
∴∠3+∠2=∠MAB+∠PBN=90°;
∴AE⊥BF.故错误.
故选:C.
4.【解答】解:由题意可知,△ABC的边AC上的高是线段BD.
故选:C.
5.【解答】解:∵过一个多边形的一个顶点的对角线有6条,
∴多边形的边数为6+3=9,
∴这个多边形是九边形.
∴该多边形对角线一共有:=27(条).
故选:D.
6.【解答】解:∵直线a∥b∥c,直线d与它们分别垂直且相交于A,B,C三点,
∴AB长为直线a和b之间的距离,BC长为直线b和c之间的距离,AC长为直线a和c之间的距离,
又∵AB=2,AC=6,
∴BC=6﹣2=4,
即平行线b、c之间的距离是4.
故选:B.
7.【解答】解:②由∠DAC=∠BCA可得AD∥BC,
④由∠ADB=∠CBD可得AD∥BC,
故选:C.
8.【解答】解:∵直线a∥b,
∴∠1+∠BCA+∠2+∠BAC=180°,
∵∠BAC=30°,∠BCA=90°,∠1=20°,
∴∠2=40°.
故选:C.
9.【解答】解:如图,过E作EF∥AB,
则AB∥EF∥CD,
∴∠3=∠1,∠2=∠4,
∵∠3+∠4=60°,
∴∠1+∠2=60°,
∵∠1=30°,
∴∠2=30°,
故选:D.
10.【解答】解:设这个多边形为n边形,由题意得,
(n﹣2)×180°=360°×2﹣180°,
解得n=5,
即这个多边形为五边形,
故选:A.
11.【解答】解:∵∠ECD是△BCE的一个外角,
∴∠ECD=∠B+∠E=35°+25°=60°,
∵CE平分∠ACD,
∴∠ACD=2∠ECD=120°,
故选:C.
12.【解答】解:过E、F分别作EM∥AB,FN∥AB,
∵AB∥CD,
∴CD∥EM,CD∥FN,
∴∠CDE=∠DEM,∠ABE=∠BEM,∠CDF=∠DFN,∠ABF=∠BFN,
∴∠DEB=∠CDE+∠ABE,∠DFB=∠CDF+∠ABF,
∵∠CDF=∠CDE,∠ABF=∠ABE
∴∠DFB=∠CDE+∠ABE=∠DEB,
∴∠DEB:∠DFB=3:2,
故选:D.
二.填空题(共7小题,满分28分)
13.【解答】解:为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的稳定性,
故答案为:稳定.
14.【解答】解:DE、BC被AB所截,∠ADE与∠B是同位角;
DC、BC被AB所截,∠ADC与∠B是同位角.
故图中有两对同位角.
15.【解答】解:由题意得正n边形的每一个外角为180°﹣144°=36°,
n=360°÷36°=10,
故答案为10.
16.【解答】解:∵△ABC沿着射线BC的方向平移,得到△DEF,
∴BE=CF,
∵EF=13,EC=7,
∴BE+7+CF=13,
即2BE+7=13,解得BE=3,
即平移的距离为3.
故答案为3.
17.【解答】解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
18.【解答】解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠ACE=∠A+∠ABC=40°+2∠CBD,
∴∠DCE+∠ACD=∠A+2∠CBD,
∵∠DCE=∠CBD+∠D,∠A=∠D=40°,∠ACD=30°,
∴∠DCE+30°=40°+2∠CBD,即∠DCE=2∠CBD+10°①,
∠DCE=40°+∠CBD②,
由①②得∠DCE=70°,
故答案为:70°.
19.【解答】解:第一个图形有2×12=2个小平行四边形,
第二个图形有2×22=8个小平行四边形,
第三个图形有2×32=18个小平行四边形,
…
第n个图形有2n2个小平行四边形,
第18个图形有2×182=648个小平行四边形.
故答案为:648.
三.解答题(共7小题,满分56分)
20.【解答】解:∵∠COF+∠C=180°,
∴EF∥CD,
∵∠C=∠B,
∴AB∥CD,
∴AB∥EF.
21.【解答】解:∵AD是△ABC的高线,
∴∠ADC=90°,
∵∠ADC+∠C+∠CAD=180°,∠C=70°,
∴∠CAD=180°﹣90°﹣70°=20°;
∵∠ABC+∠C+∠CAB=180°,∠C=70°,∠BAC=50°,
∴∠ABC=180°﹣70°﹣50°=60°,
∵AE,BF分别平分∠BAC,∠ABC,AE,BF相交于点O,
∴∠BAO=∠BAC=25°,∠ABO=∠ABC=30°,
∵∠ABO+∠BAO+∠AOB=180°,
∴∠AOB=180°﹣25°﹣30°=125°.
22.【解答】解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
23.【解答】解:(1)∵AB∥CD,
∴∠1=∠DCE=32°,
∵CE平分∠ACD,
∴∠ACE=∠DCE=32°;
(2)∵CF⊥CE,
∴∠FCE=90°,
∴∠FCH=90°﹣32°=58°,
∵∠2=58°,
∴∠FCH=∠2,
∴CF∥AG.
24.【解答】(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
25.【解答】解:(1)∵∠AOB+∠A+∠B=∠COD+∠C+∠D=180°,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D,
故答案为∠A+∠B=∠C+∠D;
(2)∵AP、CP分别平分∠BAD、∠BCD,
∴∠BAP=∠DAP,∠BCP=∠DCP,
由(1)可得:∠BAP+∠B=∠BCP+∠P,∠DAP+∠P=∠DCP+∠D,
∴∠B﹣∠P=∠P﹣∠D,
即2∠P=∠B+∠D,
∵∠B=36°,∠D=14°,
∴∠P=25°;
(3)2∠P=∠B+∠D.
理由:∵CP、AG分别平分∠BCE、∠FAD,
∴∠ECP=∠PCB,∠FAG=∠GAD,
∵∠PAB=∠FAG,
∴∠GAD=∠PAB,
∵∠P+∠PAB=∠B+∠PCB,
∴∠P+∠GAD=∠B+∠PCB,
∵∠P+∠PAD=∠D+∠PCD,
∴∠P+(180°﹣∠GAD)=∠D+(180°﹣∠ECP),
∴2∠P=∠B+∠D.
26.【解答】解:(1)∵∠MON=60°,
∴∠BAO+∠ABO=120°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=60°,
∴∠ACG=∠CBA+∠CAB=60°,
故答案为:60°;
(2)∵∠MON=n°,
∴∠BAO+∠ABO=180°﹣n°,
∵AC、BC分别是∠BAO和∠ABO的角平分线,
∴∠CBA=∠ABO,∠CAB=∠BAO,
∴∠CBA+∠CAB=(∠ABO+∠BAO)=90°﹣n°,
∴∠ACG=∠CBA+∠CAB=90°﹣n°;
(3)∵CF∥OA,
∴∠ACF=∠CAG,
∴∠BGO﹣∠ACF=∠BGO﹣∠CAG=∠ACG=90°﹣80°=50°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
