2020-2021学年八年级数学人教版下册 17.1勾股定理 同步测试(word版,含答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册 17.1勾股定理 同步测试(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 252.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 10:45:23 | ||
图片预览

文档简介
17.1勾股定理
同步测试
一、单选题
1.若直角三角形中,斜边的长为17,一条直角边长为15,则另一条直角边长为(
)
A.7
B.8
C.20
D.65
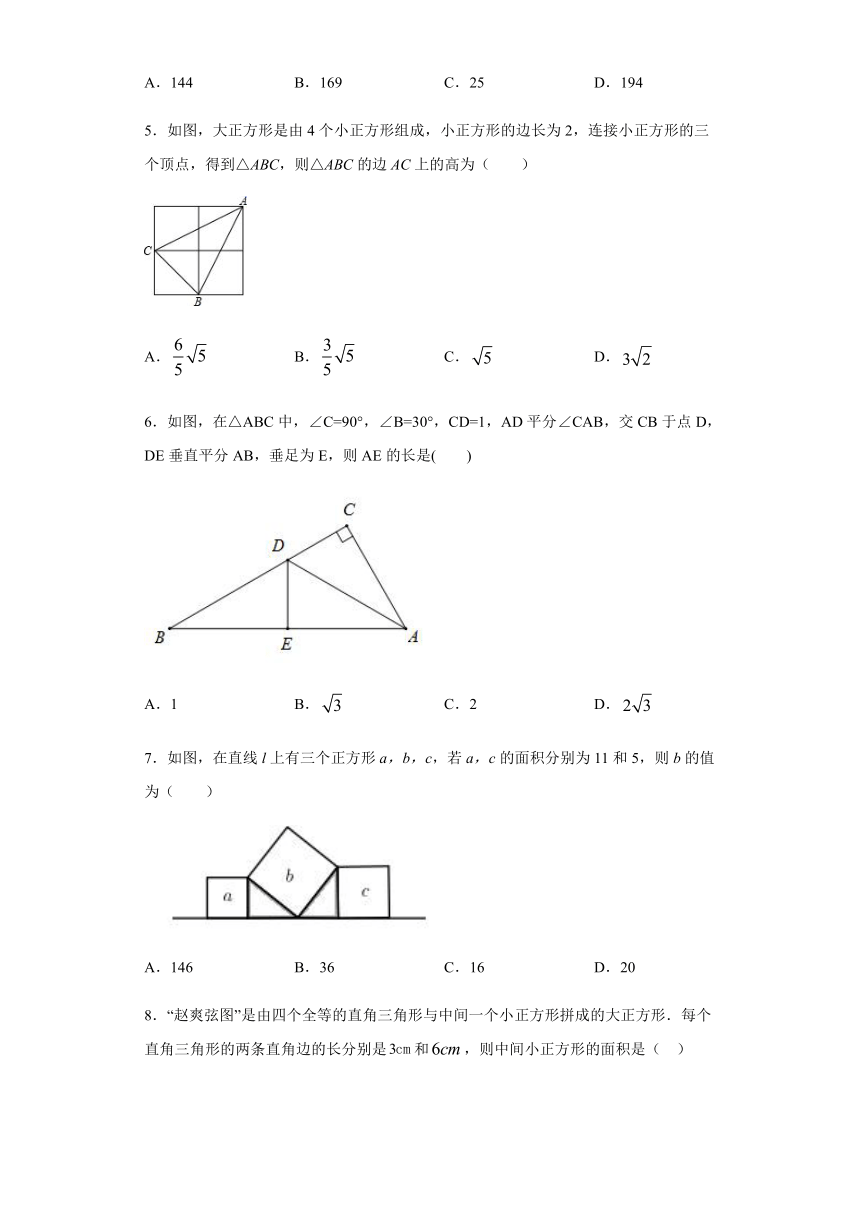
2.利用勾股定理,可以作出长为无理数的线段.如图,在数轴上找到点,使,过点作直线垂直于,在上取点,使,以原点为圆心,以长为半径作弧,弧与数轴的交点为,那么点表示的无理数是(
)
A.
B.
C.
D.
3.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB于D,则CD的长是(
)
A.5
B.7
C.
D.
4.如图,已知正方形A的面积为25,正方形C的面积为169,那么正方形B的面积是(
)
A.144
B.169
C.25
D.194
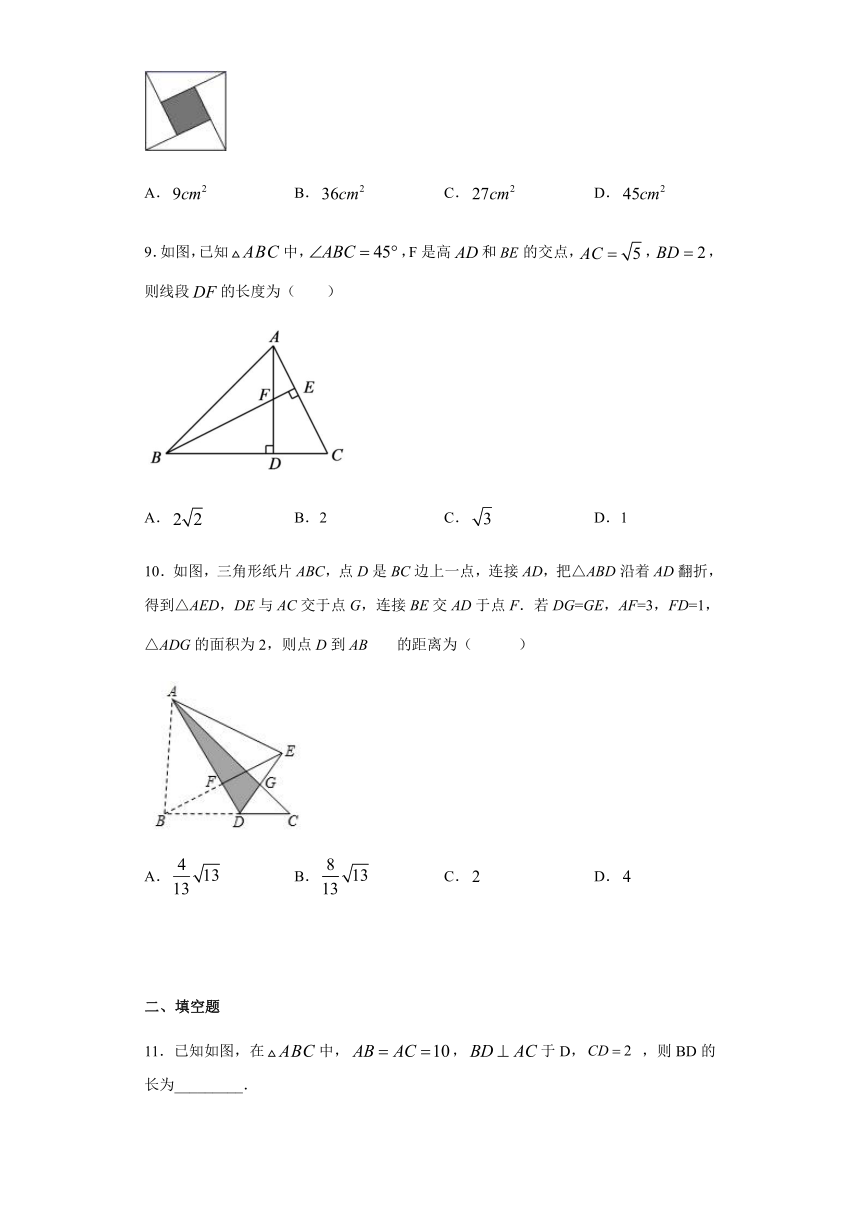
5.如图,大正方形是由4个小正方形组成,小正方形的边长为2,连接小正方形的三个顶点,得到△ABC,则△ABC的边AC上的高为( )
A.
B.
C.
D.
6.如图,在△ABC中,∠C=90°,∠B=30°,CD=1,AD平分∠CAB,交CB于点D,DE垂直平分AB,垂足为E,则AE的长是(
)
A.1
B.
C.2
D.
7.如图,在直线l上有三个正方形a,b,c,若a,c的面积分别为11和5,则b的值为(
)
A.146
B.36
C.16
D.20
8.“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的大正方形.每个直角三角形的两条直角边的长分别是和,则中间小正方形的面积是(
)
A.
B.
C.
D.
9.如图,已知中,,F是高和的交点,,,则线段的长度为(
)
A.
B.2
C.
D.1
10.如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,FD=1,△ADG的面积为2,则点D到AB的距离为( )
A.
B.
C.
D.
二、填空题
11.已知如图,在中,,于D,
,则BD的长为_________.
12.在中,斜边则的值为____________.
13.如图,要为一段高5m,长13m的楼梯铺上红地毯,至少需要红地毯______m.
14.如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是边BC的中点,AD=ED=3,则BC的长为________.
15.如图中的螺旋由一系列直角三角形组成,则线段的长度为__________.
三、解答题
16.如图,在中,
,为边上一点,且,.
(1)求的长;
(2)若,求的面积.
17.如图,方格中小正方形的边长为1,的三个顶点都在小正方形的格点上,求:
(1)的面积.
(2)点到边的距离.
18.已知:如图,,,连结交于点.
(1)求证:;
(2)若,,求边的长.
参考答案
1.B
2.B
3.C
4.A
5.A
6.B
7.C
8.A
9.D
10.B
11.6
12.10
13.17
14.
15.
16.(1);(2)45.
17.(1).(2).
18.(1)略;(2)
同步测试
一、单选题
1.若直角三角形中,斜边的长为17,一条直角边长为15,则另一条直角边长为(
)
A.7
B.8
C.20
D.65
2.利用勾股定理,可以作出长为无理数的线段.如图,在数轴上找到点,使,过点作直线垂直于,在上取点,使,以原点为圆心,以长为半径作弧,弧与数轴的交点为,那么点表示的无理数是(
)
A.
B.
C.
D.
3.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB于D,则CD的长是(
)
A.5
B.7
C.
D.
4.如图,已知正方形A的面积为25,正方形C的面积为169,那么正方形B的面积是(
)
A.144
B.169
C.25
D.194
5.如图,大正方形是由4个小正方形组成,小正方形的边长为2,连接小正方形的三个顶点,得到△ABC,则△ABC的边AC上的高为( )
A.
B.
C.
D.
6.如图,在△ABC中,∠C=90°,∠B=30°,CD=1,AD平分∠CAB,交CB于点D,DE垂直平分AB,垂足为E,则AE的长是(
)
A.1
B.
C.2
D.
7.如图,在直线l上有三个正方形a,b,c,若a,c的面积分别为11和5,则b的值为(
)
A.146
B.36
C.16
D.20
8.“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的大正方形.每个直角三角形的两条直角边的长分别是和,则中间小正方形的面积是(
)
A.
B.
C.
D.
9.如图,已知中,,F是高和的交点,,,则线段的长度为(
)
A.
B.2
C.
D.1
10.如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,FD=1,△ADG的面积为2,则点D到AB的距离为( )
A.
B.
C.
D.
二、填空题
11.已知如图,在中,,于D,
,则BD的长为_________.
12.在中,斜边则的值为____________.
13.如图,要为一段高5m,长13m的楼梯铺上红地毯,至少需要红地毯______m.
14.如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是边BC的中点,AD=ED=3,则BC的长为________.
15.如图中的螺旋由一系列直角三角形组成,则线段的长度为__________.
三、解答题
16.如图,在中,
,为边上一点,且,.
(1)求的长;
(2)若,求的面积.
17.如图,方格中小正方形的边长为1,的三个顶点都在小正方形的格点上,求:
(1)的面积.
(2)点到边的距离.
18.已知:如图,,,连结交于点.
(1)求证:;
(2)若,,求边的长.
参考答案
1.B
2.B
3.C
4.A
5.A
6.B
7.C
8.A
9.D
10.B
11.6
12.10
13.17
14.
15.
16.(1);(2)45.
17.(1).(2).
18.(1)略;(2)
