人教版数学七年级下册 5.3.1平行线的判定和性质讲义(含解析)
文档属性
| 名称 | 人教版数学七年级下册 5.3.1平行线的判定和性质讲义(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 734.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 00:00:00 | ||
图片预览



文档简介
平行线的判定和性质
知识互联网
平行的定义、性质及判定
平行公理及推论
基本模型中平行线的证明
课堂思维碰撞
题型一:平行线的定义、性质及判定
思路导航
定
义
示例剖析
平行线的概念:在同一平面内,永不相交的两条直线称为平行线.用“”表示.
,等.
平行线的性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
若,则;
若,则;
若,则.
平行线的判定:
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行.
若,则;
若,则;
若,则.
平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
简单说成:过一点有且只有一条直线与已知直线平行.
过直线外一点做,,则与重合.
平行公理推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
简单说成:平行于同一条直线的两条直线平行.
若,则.
典例精讲
题型一
例1.下列说法正确的是()
A.两条直线不平行则相交
B.在同一个平面内,没有公共点的两条射线必平行
C.在同一个平面内,若两条线段平行,它们不相交
D.在同一个平面内,若两条线段没有公共点,则它们平行
故选C
题点精练
1.在同一平面内,不重合的两条直线的位置关系是( )
A.平行
B.相交
C.平行或相交
D.平行、相交或垂直
故选C
2.下列说法正确的是( )
A.同一平面内没有公共点的两条线段平行B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
故选C
题型二
平行线画法:
①一落:把三角板的一边落在已知直线上
②二靠:紧靠三角板的另一边放直尺
③三移:沿直尺移动三角板,使得原来落在已知直线上的那一边过已知点
④四画:沿原来落在已知直线上的那一边画直线
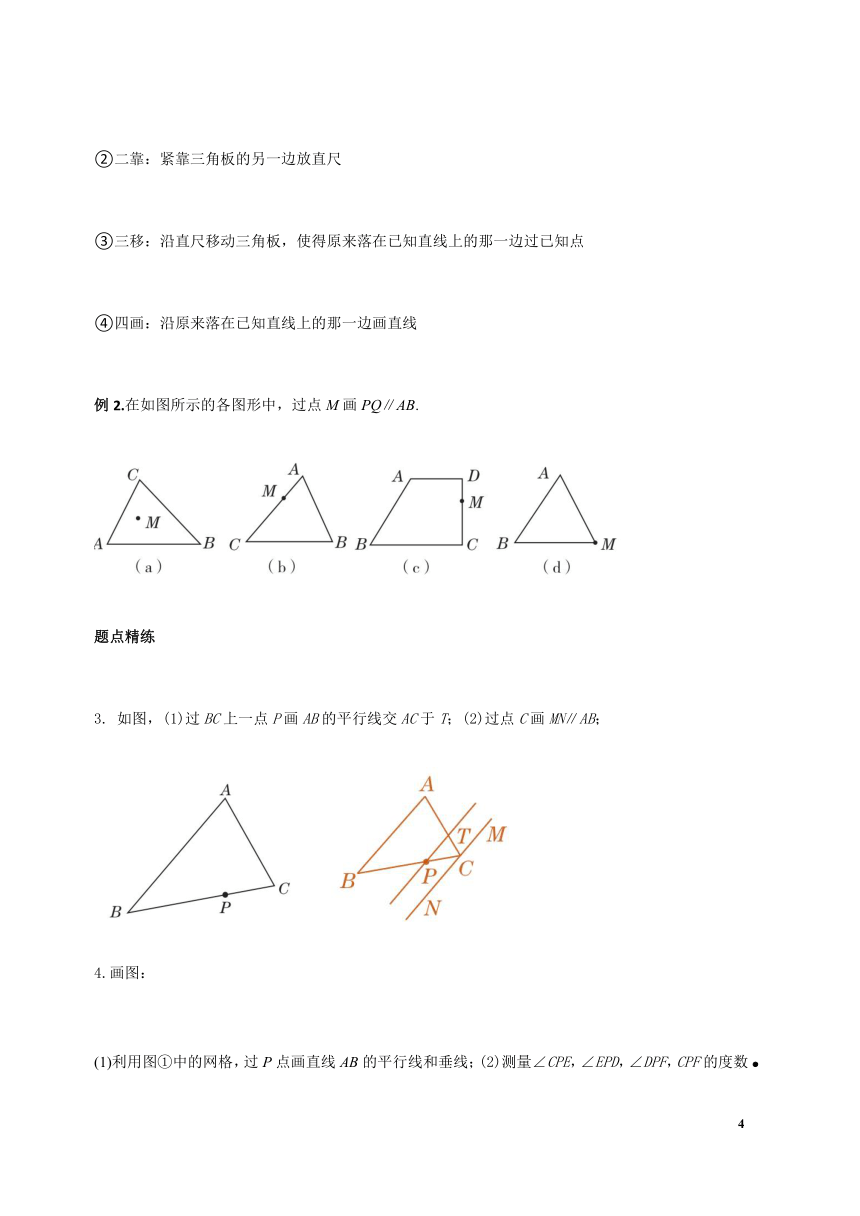
例2.在如图所示的各图形中,过点M画PQ∥AB.
题点精练
如图,(1)过BC上一点P画AB的平行线交AC于T;(2)过点C画MN∥AB;
4.画图:
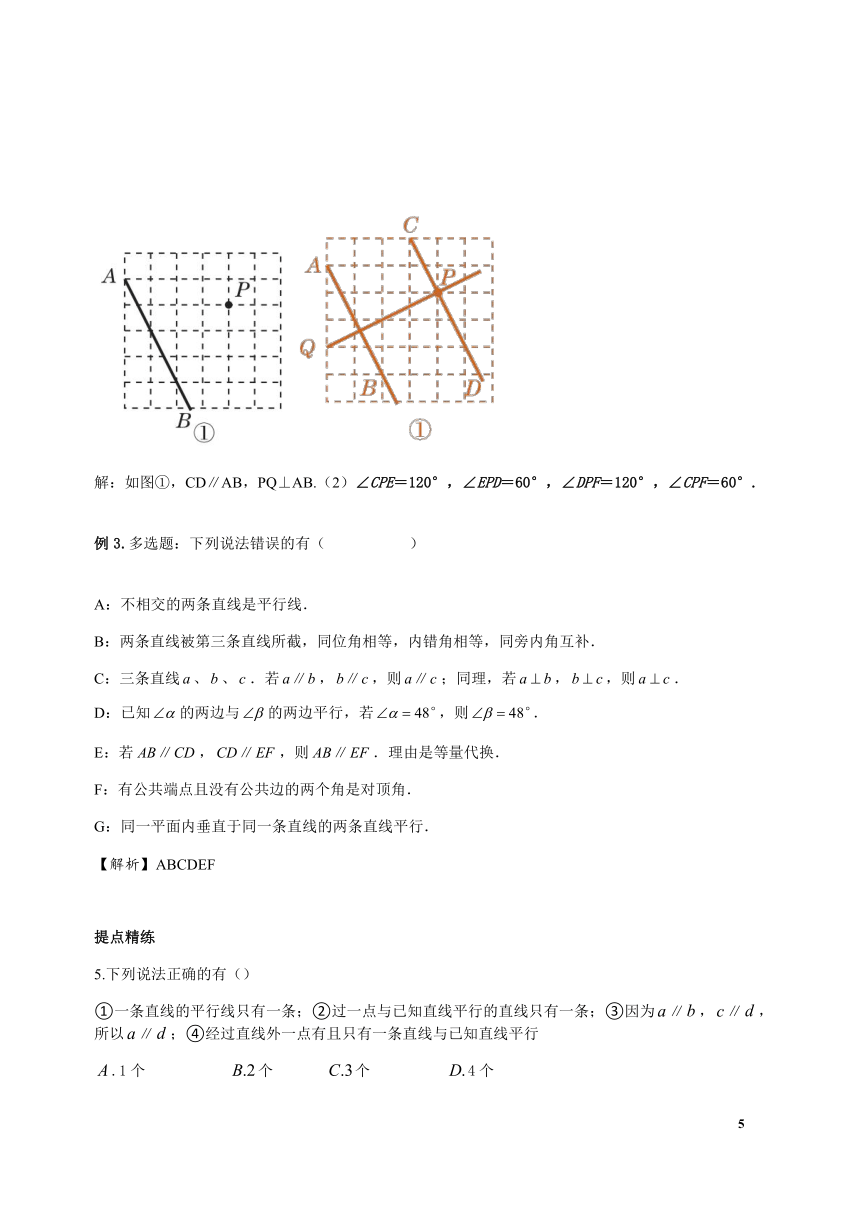
(1)利用图①中的网格,过P点画直线AB的平行线和垂线;(2)测量∠CPE,∠EPD,∠DPF,CPF的度数.
解:如图①,CD∥AB,PQ⊥AB.(2)∠CPE=120°,∠EPD=60°,∠DPF=120°,∠CPF=60°.
例3.多选题:下列说法错误的有(
)
A:不相交的两条直线是平行线.
B:两条直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补.
C:三条直线、、.若,,则;同理,若,,则.
D:已知的两边与的两边平行,若,则.
E:若,,则.理由是等量代换.
F:有公共端点且没有公共边的两个角是对顶角.
G:同一平面内垂直于同一条直线的两条直线平行.
ABCDEF
提点精练
5.下列说法正确的有()
①一条直线的平行线只有一条;②过一点与已知直线平行的直线只有一条;③因为∥,∥,所以∥;④经过直线外一点有且只有一条直线与已知直线平行
.1个
个
个
4个
解析:1-43错,4对故选A
6.下列说法正确的是( )
A.两条不相交的直线叫做平行线B.过一点有且只有一条直线与已知直线平行
C.在同一平面内不相交的两条线段互相平行D.在同一平面内不相交的两条直线叫做平行线
【点拨】对平行线定义的理解要抓住三个关键要素:“同一平面内”“不相交”“直线”,本题易错之处在于理解平行线定义时,容易只关注其中一个或两个要素而导致判断错误故选D
例4.如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
题点精练
7.如图,不添加辅助线,请写出一个能判定的
条件:
.
8如图,点在的延长线上,给出下列条件:
①
;②
;③
;
④
;⑤
;
⑥
;⑦
.
能说明的条件有
.
故是②④⑤;
9.如图,已知AB⊥BD于点B,CD⊥BD于点D,∠1=∠2,试问CD与EF平行吗?为什么?
解:CD∥EF.理由:因为∠1=∠2(__________),
所以AB∥EF(________________________________).
因为AB⊥BD,CD⊥BD,
所以AB∥CD(____________________________________
__________________________).
所以CD∥EF(____________________________________).
第3空
在同一平面内,垂直于同一条直线的两条直线互相平行
10.【2020·金华】如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b.理由是( )
A.连接直线外一点与直线上各点的所有线段中,垂线段最短
B.在同一平面内,垂直于同一条直线的两条直线互相平行
C.在同一平面内,过一点有一条而且仅有一条直线垂直于已
知直线
D.经过直线外一点,有且只有一条直线与这条直线平行
故选B
已知:如图,AB⊥BC,CD⊥BC,∠1=∠2,BE与CF平行吗?请说明理由.
解:BE∥CF.理由如下:
∵AB⊥BC,CD⊥BC(__________________),∴∠ABC=∠BCD=________°(垂直的定义).
∵∠1=∠2(______________),∴∠EBC=∠FCB(______________________).
∴BE∥CF(______________________________).
解析:已知;已知;90度;等角的余角想等;内错角想等,两直线平行.
12.在下面的括号内填上理由.
已知:如图,直线NF与直线HB,CD分别交于点E,F,直线AM与直线HB交于点A,且∠1=∠4=105°,∠2=75°.试说明:AM∥NF,AB∥CD.
解:∵∠2=∠3(__________),∠2=75°(已知),∴∠3=75°.
∵∠1=105°(已知),∴∠MAB=180°-∠1=75°.
∴∠MAB=∠3.∴AM∥NF(_____________________________).
∵∠3=75°,∠4=105°,∴∠3+∠4=180°.
∴AB∥CD(______________________________).
解析:对顶角想等;内错角想等两直线平行;同旁内角互补两直线平行
13.如图,∠1:∠2:∠3=2:3:4,∠AFE=60°,∠BDE=120°,写出图中平行的直线,并说明理由.
解析:解:DE∥AB,EF∥BC.理由:设∠1=2x°,则∠2=3x°,∠3=4x°,
∵∠1+∠2+∠3=180°,∴2x°+3x°+4x°=180°,解得x°=20°.
∴∠2=60°.∵∠AFE=60°,∴∠AFE=∠2=60°.∴DE∥AB.∵∠BDE=120°,
∴∠BDE+∠2=120°+60°=180°.∴EF∥BC.
14.如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,试判断AB与CD的位置关系,并说明理由.
【点拨】利用整体思想,将∠1+∠2=90°看成一个整体,求得∠ABD+∠CDB=180°,再由同旁内角互补,两直线平行,判断AB∥CD.
解:AB∥CD.理由如下:因为B.E平分∠ABD,DE平分∠BDC,
∠1+∠2=90°,所以∠ABD+∠BDC=2∠1+2∠2=2(∠1+∠2)=180°.
所以AB∥CD(同旁内角互补,两直线平行)
15.如图,以下四个条件:
①∠1=∠3,②∠2=∠4,
③∠BAD+∠D=180°,
④∠EAD=∠B.
其中,能够判定AB∥DC的有( )
A.①③
B.③④
C.①②
D.②④
【点拨】若∠1=∠3,则AB∥DC;若∠2=∠4,则AD∥BC;
若∠BAD+∠D=180°,则AB∥DC;若∠EAD=∠B,则AD∥BC.
选A
题型三:平行线的性质
例5..【2020·铜仁】如图,直线AB∥CD,∠3=70°,则∠1=( )
A.70°
B.100°
C.110°
D.120°
故选C
例6.【2020·枣庄】一副直角三角尺如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A.10°
B.15°
C.18°
D.
【2019·南通】如图,AB∥CD,AE平分∠CAB
交CD于点E,若∠C=70°,则∠AED的度数为( )
A.110°
B.125°
C.135°
D.140°
解析:【点拨】∵AB∥CD,∴∠C+∠CAB=180°.∵∠C=70°,
∴∠CAB=110°.∵AE平分∠CAB,∴∠BAE=∠CAB=55°.又∵AB∥CD,∴∠AED=180°-∠BAE=180°-55°=125°.
16.【中考·重庆B卷】如图,AB∥CD,三角形EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,GE平分∠FGD.若∠EFG=90°,∠E=35°,求∠EFB的度数.
解:∵在三角形EFG中,∠EFG=90°,∠E=35°,
∴∠EGF=180°-90°-35°=55°.∵GE平分∠FGD,∴∠EGF=∠EGD=55°.
∵AB∥CD,∴∠EHB=∠EGD=55°.又∵∠EHB=180°-∠AHE=∠EFB+∠E,
∴∠EFB=∠EHB-∠E=55°-35°=20°.
如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠3.AD是∠BAC的平分线吗?若是,请说明理由.
解:AD是∠BAC的平分线.理由如下:
∵AD⊥BC,EG⊥BC,∴EG∥AD.∴∠3=∠1,∠E=∠2.
又∵∠E=∠3,∴∠1=∠2,即AD是∠BAC的平分线.
18.如图,已知AB∥CD,EF⊥AB于点O,∠FGC=125°,求∠EFG的度数.下面提供三种思路:
(1)过点F作FH∥AB;(2)延长OF交CD于点M;(3)延长GF交AB于点K.
请你利用三种思路中的两种思路,将图形补充完整,并求∠EFG的度数.
解:利用思路(1).过点F作FH∥AB,如图①.∵EF⊥AB,
∴∠BOF=90°.∵FH∥AB,∴∠HFO=∠BOF=90°.∵AB∥CD,∴FH∥CD,∴∠FGC+∠GFH=180°.∵∠FGC=125°,
∴∠GFH=55°,∴∠EFG=∠GFH+∠HFO=55°+90°=145°.
题型四
模
型
示例剖析
若,则
若,则
若,则
若,则
例7.已知:如图,点为其内部任意一点,
求证:.
解析:过点作,
∵,(已知)
∴(平行于同一条直线的两直线平行)
∵,(已知)
∴(两直线平行,内错角相等)
∵,(已知)
∴(两直线平行,内错角相等)
∵
∴(等量代换)
例8.如图,已知,,,
求的度数.
解析:过点作.
∵且(已知)
∴(平行于同一条直线的两直线平行)
∵且(已知)
∴(两直线平行,内错角相等)
∵且(已知)
∴(两直线平行,同旁内角互补)
∴
【拓展】如图所示,已知直线,直线和直线、交于、两点,在、之间有一点,如果点在、之间运动,问、、之间有怎样的关系?
这种关系是否发生变化?试着证明你的结论.
解析:.
关系不变.
提示:过点做直线.
例9.如图,已知,,
,求的度数.
解析:如图延长交直线于点
∵,(已知)
(对顶角相等)
∴(等量代换)
∴,(同旁内角互补,两直线平行)
∴(两直线平行,内错角相等)
∵,(已知)
∴(等量代换)
∴,(同位角相等,两直线平行)
∴(两直线平行,同旁内角互补)
∵,
∴
【点评】通过辅助线将相关角联系起来.
题点精练
19.【2020·南通】如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( )
A.36°
B.34°C.32°
D.30°
【点拨】如图,过点E作EF∥AB,则EF∥CD.
∵EF∥AB,∴∠AEF=∠A=54°.∴∠CEF=∠AEF-∠AEC=54°-18°=36°.
又∵EF∥CD,∴∠C=∠CEF=36°.
20.【2020·常德】如图,已知AB∥DE,∠1=30°,∠2=35°,则∠BCE的度数为( )
A.70°
B.65°
C.35°
D.5°
【点拨】如图,作CF∥AB,∵AB∥DE,∴CF∥DE.
∴AB∥CF∥DE.∴∠1=∠BCF,∠FCE=∠2.∵∠1=30°,
∠2=35°,∴∠BCF=30°,∠FCE=35°.∴∠BCE=65°.
21.如图,A,B两岛位于东西方向的一条水平线上,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,求∠ACB的度数.
解:如图,过点A,C,B分别画出南北方向的方向线,由题意,得∠EAC=50°,∠FBC=40°.∵AE∥DC∥BF,∴∠ACD=∠EAC=50°,∠BCD=∠FBC=40°.∴∠ACB=∠ACD+∠BCD=50°+40°=90°.
22.阅读下列解题过程,然后解答后面的问题.
如图①,已知AB∥CD,∠B=35°,∠D=32°,求∠BED的度数
(1)如图②,已知∠D=30°,∠ACD=65°,为了保证AB∥DE,∠A应多大?
(2)如图③,要使GP∥HQ,则∠G,∠GFH,∠H之间有什么关系?
解:如图①,过点E作EF∥AB.
则AB∥CD∥EF.因为AB∥EF,所以∠1=∠B=35°.
因为CD∥EF,所以∠2=∠D=32°.所以∠BED=∠1+∠2=35°+32°=67°.
如图②③是明明设计的智力拼图玩具的一部分,现在明明遇到两个问题,请你帮他解决.
解:如图①,过点C作CF∥DE,则∠2=∠D=30°.因为∠ACD=65°,即∠1+∠2=65°,所以∠1=65°-∠2=65°-30°=35°.因为AB∥DE,CF∥DE,所以AB∥CF,所以∠A=∠1=35°.
解:如图②,过点F作FI∥GP,则∠G+∠1=180°.因为GP∥HQ,FI∥GP,所以HQ∥FI.所以∠2+∠H=180°,所以∠G+∠1+∠2+∠H=360°,即∠G+∠GFH+∠H=360°.
23.如图,
AB∥CD,BN,DN分别平分∠ABM,∠MDC,则∠BMD与∠N之间的数量关系如何?请说明理由.
解:∠BMD=2∠N.理由如下:如图,过点M作ME∥AB,则∠ABM=∠BME.
∵AB∥CD,ME∥AB,∴ME∥CD.∴∠CDM=∠DME.∴∠ABM+∠CDM=∠BME+∠DME=∠BMD.
同理∠N=∠ABN+∠CDN.∵BN,DN分别平分∠ABM,∠MDC,
∴∠ABM=2∠ABN,∠CDM=2∠CDN.∴∠ABM+∠CDM=2∠ABN+2∠CDN.∴∠BMD=2∠N.
24.【2020·武汉】如图,直线EF分别与直线AB,CD相交于点E,F.EM平分∠BEF,FN平分∠CFE,且EM∥FN.求证:AB∥CD.
证明:∵EM∥FN,∴∠FEM=∠EFN.又∵EM平分∠BEF,FN平分∠CFE,
∴∠FEB=∠EFC.∴AB∥CD.
如图,已知∠ABC,请你再画一个∠DEF,使DE∥AB,EF∥BC,且DE交BC边于点P.探究:∠ABC与∠DEF有怎样的数量关系?并说明理由.
解:画图如图①②③④所示.∠ABC与∠DEF相等或互补,
理由如下:如图①,∵AB∥DE,∴∠ABC=∠DPC.∵BC∥EF,∴∠DEF=∠DPC.∴∠ABC=∠DEF.
如图②,∵AB∥DE,∴∠ABC=∠EPC.∵BC∥EF,∴∠EPC=∠DEF.∴∠ABC=∠DEF.
如图③,∵AB∥DE,∴∠ABC=∠BPE.∵BC∥EF,∴∠DEF+∠BPE=180°.∴∠ABC+∠DEF=180°.
如图④,∵AB∥DE,∴∠ABC=∠EPC.∵BC∥EF,∴∠EPC+∠DEF=180°.∴∠ABC+∠DEF=180°.
综上可知,∠ABC与∠DEF相等或互补.
1
2
1
知识互联网
平行的定义、性质及判定
平行公理及推论
基本模型中平行线的证明
课堂思维碰撞
题型一:平行线的定义、性质及判定
思路导航
定
义
示例剖析
平行线的概念:在同一平面内,永不相交的两条直线称为平行线.用“”表示.
,等.
平行线的性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
若,则;
若,则;
若,则.
平行线的判定:
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行.
若,则;
若,则;
若,则.
平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
简单说成:过一点有且只有一条直线与已知直线平行.
过直线外一点做,,则与重合.
平行公理推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
简单说成:平行于同一条直线的两条直线平行.
若,则.
典例精讲
题型一
例1.下列说法正确的是()
A.两条直线不平行则相交
B.在同一个平面内,没有公共点的两条射线必平行
C.在同一个平面内,若两条线段平行,它们不相交
D.在同一个平面内,若两条线段没有公共点,则它们平行
故选C
题点精练
1.在同一平面内,不重合的两条直线的位置关系是( )
A.平行
B.相交
C.平行或相交
D.平行、相交或垂直
故选C
2.下列说法正确的是( )
A.同一平面内没有公共点的两条线段平行B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
故选C
题型二
平行线画法:
①一落:把三角板的一边落在已知直线上
②二靠:紧靠三角板的另一边放直尺
③三移:沿直尺移动三角板,使得原来落在已知直线上的那一边过已知点
④四画:沿原来落在已知直线上的那一边画直线
例2.在如图所示的各图形中,过点M画PQ∥AB.
题点精练
如图,(1)过BC上一点P画AB的平行线交AC于T;(2)过点C画MN∥AB;
4.画图:
(1)利用图①中的网格,过P点画直线AB的平行线和垂线;(2)测量∠CPE,∠EPD,∠DPF,CPF的度数.
解:如图①,CD∥AB,PQ⊥AB.(2)∠CPE=120°,∠EPD=60°,∠DPF=120°,∠CPF=60°.
例3.多选题:下列说法错误的有(
)
A:不相交的两条直线是平行线.
B:两条直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补.
C:三条直线、、.若,,则;同理,若,,则.
D:已知的两边与的两边平行,若,则.
E:若,,则.理由是等量代换.
F:有公共端点且没有公共边的两个角是对顶角.
G:同一平面内垂直于同一条直线的两条直线平行.
ABCDEF
提点精练
5.下列说法正确的有()
①一条直线的平行线只有一条;②过一点与已知直线平行的直线只有一条;③因为∥,∥,所以∥;④经过直线外一点有且只有一条直线与已知直线平行
.1个
个
个
4个
解析:1-43错,4对故选A
6.下列说法正确的是( )
A.两条不相交的直线叫做平行线B.过一点有且只有一条直线与已知直线平行
C.在同一平面内不相交的两条线段互相平行D.在同一平面内不相交的两条直线叫做平行线
【点拨】对平行线定义的理解要抓住三个关键要素:“同一平面内”“不相交”“直线”,本题易错之处在于理解平行线定义时,容易只关注其中一个或两个要素而导致判断错误故选D
例4.如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
题点精练
7.如图,不添加辅助线,请写出一个能判定的
条件:
.
8如图,点在的延长线上,给出下列条件:
①
;②
;③
;
④
;⑤
;
⑥
;⑦
.
能说明的条件有
.
故是②④⑤;
9.如图,已知AB⊥BD于点B,CD⊥BD于点D,∠1=∠2,试问CD与EF平行吗?为什么?
解:CD∥EF.理由:因为∠1=∠2(__________),
所以AB∥EF(________________________________).
因为AB⊥BD,CD⊥BD,
所以AB∥CD(____________________________________
__________________________).
所以CD∥EF(____________________________________).
第3空
在同一平面内,垂直于同一条直线的两条直线互相平行
10.【2020·金华】如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b.理由是( )
A.连接直线外一点与直线上各点的所有线段中,垂线段最短
B.在同一平面内,垂直于同一条直线的两条直线互相平行
C.在同一平面内,过一点有一条而且仅有一条直线垂直于已
知直线
D.经过直线外一点,有且只有一条直线与这条直线平行
故选B
已知:如图,AB⊥BC,CD⊥BC,∠1=∠2,BE与CF平行吗?请说明理由.
解:BE∥CF.理由如下:
∵AB⊥BC,CD⊥BC(__________________),∴∠ABC=∠BCD=________°(垂直的定义).
∵∠1=∠2(______________),∴∠EBC=∠FCB(______________________).
∴BE∥CF(______________________________).
解析:已知;已知;90度;等角的余角想等;内错角想等,两直线平行.
12.在下面的括号内填上理由.
已知:如图,直线NF与直线HB,CD分别交于点E,F,直线AM与直线HB交于点A,且∠1=∠4=105°,∠2=75°.试说明:AM∥NF,AB∥CD.
解:∵∠2=∠3(__________),∠2=75°(已知),∴∠3=75°.
∵∠1=105°(已知),∴∠MAB=180°-∠1=75°.
∴∠MAB=∠3.∴AM∥NF(_____________________________).
∵∠3=75°,∠4=105°,∴∠3+∠4=180°.
∴AB∥CD(______________________________).
解析:对顶角想等;内错角想等两直线平行;同旁内角互补两直线平行
13.如图,∠1:∠2:∠3=2:3:4,∠AFE=60°,∠BDE=120°,写出图中平行的直线,并说明理由.
解析:解:DE∥AB,EF∥BC.理由:设∠1=2x°,则∠2=3x°,∠3=4x°,
∵∠1+∠2+∠3=180°,∴2x°+3x°+4x°=180°,解得x°=20°.
∴∠2=60°.∵∠AFE=60°,∴∠AFE=∠2=60°.∴DE∥AB.∵∠BDE=120°,
∴∠BDE+∠2=120°+60°=180°.∴EF∥BC.
14.如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,试判断AB与CD的位置关系,并说明理由.
【点拨】利用整体思想,将∠1+∠2=90°看成一个整体,求得∠ABD+∠CDB=180°,再由同旁内角互补,两直线平行,判断AB∥CD.
解:AB∥CD.理由如下:因为B.E平分∠ABD,DE平分∠BDC,
∠1+∠2=90°,所以∠ABD+∠BDC=2∠1+2∠2=2(∠1+∠2)=180°.
所以AB∥CD(同旁内角互补,两直线平行)
15.如图,以下四个条件:
①∠1=∠3,②∠2=∠4,
③∠BAD+∠D=180°,
④∠EAD=∠B.
其中,能够判定AB∥DC的有( )
A.①③
B.③④
C.①②
D.②④
【点拨】若∠1=∠3,则AB∥DC;若∠2=∠4,则AD∥BC;
若∠BAD+∠D=180°,则AB∥DC;若∠EAD=∠B,则AD∥BC.
选A
题型三:平行线的性质
例5..【2020·铜仁】如图,直线AB∥CD,∠3=70°,则∠1=( )
A.70°
B.100°
C.110°
D.120°
故选C
例6.【2020·枣庄】一副直角三角尺如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A.10°
B.15°
C.18°
D.
【2019·南通】如图,AB∥CD,AE平分∠CAB
交CD于点E,若∠C=70°,则∠AED的度数为( )
A.110°
B.125°
C.135°
D.140°
解析:【点拨】∵AB∥CD,∴∠C+∠CAB=180°.∵∠C=70°,
∴∠CAB=110°.∵AE平分∠CAB,∴∠BAE=∠CAB=55°.又∵AB∥CD,∴∠AED=180°-∠BAE=180°-55°=125°.
16.【中考·重庆B卷】如图,AB∥CD,三角形EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,GE平分∠FGD.若∠EFG=90°,∠E=35°,求∠EFB的度数.
解:∵在三角形EFG中,∠EFG=90°,∠E=35°,
∴∠EGF=180°-90°-35°=55°.∵GE平分∠FGD,∴∠EGF=∠EGD=55°.
∵AB∥CD,∴∠EHB=∠EGD=55°.又∵∠EHB=180°-∠AHE=∠EFB+∠E,
∴∠EFB=∠EHB-∠E=55°-35°=20°.
如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠3.AD是∠BAC的平分线吗?若是,请说明理由.
解:AD是∠BAC的平分线.理由如下:
∵AD⊥BC,EG⊥BC,∴EG∥AD.∴∠3=∠1,∠E=∠2.
又∵∠E=∠3,∴∠1=∠2,即AD是∠BAC的平分线.
18.如图,已知AB∥CD,EF⊥AB于点O,∠FGC=125°,求∠EFG的度数.下面提供三种思路:
(1)过点F作FH∥AB;(2)延长OF交CD于点M;(3)延长GF交AB于点K.
请你利用三种思路中的两种思路,将图形补充完整,并求∠EFG的度数.
解:利用思路(1).过点F作FH∥AB,如图①.∵EF⊥AB,
∴∠BOF=90°.∵FH∥AB,∴∠HFO=∠BOF=90°.∵AB∥CD,∴FH∥CD,∴∠FGC+∠GFH=180°.∵∠FGC=125°,
∴∠GFH=55°,∴∠EFG=∠GFH+∠HFO=55°+90°=145°.
题型四
模
型
示例剖析
若,则
若,则
若,则
若,则
例7.已知:如图,点为其内部任意一点,
求证:.
解析:过点作,
∵,(已知)
∴(平行于同一条直线的两直线平行)
∵,(已知)
∴(两直线平行,内错角相等)
∵,(已知)
∴(两直线平行,内错角相等)
∵
∴(等量代换)
例8.如图,已知,,,
求的度数.
解析:过点作.
∵且(已知)
∴(平行于同一条直线的两直线平行)
∵且(已知)
∴(两直线平行,内错角相等)
∵且(已知)
∴(两直线平行,同旁内角互补)
∴
【拓展】如图所示,已知直线,直线和直线、交于、两点,在、之间有一点,如果点在、之间运动,问、、之间有怎样的关系?
这种关系是否发生变化?试着证明你的结论.
解析:.
关系不变.
提示:过点做直线.
例9.如图,已知,,
,求的度数.
解析:如图延长交直线于点
∵,(已知)
(对顶角相等)
∴(等量代换)
∴,(同旁内角互补,两直线平行)
∴(两直线平行,内错角相等)
∵,(已知)
∴(等量代换)
∴,(同位角相等,两直线平行)
∴(两直线平行,同旁内角互补)
∵,
∴
【点评】通过辅助线将相关角联系起来.
题点精练
19.【2020·南通】如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( )
A.36°
B.34°C.32°
D.30°
【点拨】如图,过点E作EF∥AB,则EF∥CD.
∵EF∥AB,∴∠AEF=∠A=54°.∴∠CEF=∠AEF-∠AEC=54°-18°=36°.
又∵EF∥CD,∴∠C=∠CEF=36°.
20.【2020·常德】如图,已知AB∥DE,∠1=30°,∠2=35°,则∠BCE的度数为( )
A.70°
B.65°
C.35°
D.5°
【点拨】如图,作CF∥AB,∵AB∥DE,∴CF∥DE.
∴AB∥CF∥DE.∴∠1=∠BCF,∠FCE=∠2.∵∠1=30°,
∠2=35°,∴∠BCF=30°,∠FCE=35°.∴∠BCE=65°.
21.如图,A,B两岛位于东西方向的一条水平线上,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,求∠ACB的度数.
解:如图,过点A,C,B分别画出南北方向的方向线,由题意,得∠EAC=50°,∠FBC=40°.∵AE∥DC∥BF,∴∠ACD=∠EAC=50°,∠BCD=∠FBC=40°.∴∠ACB=∠ACD+∠BCD=50°+40°=90°.
22.阅读下列解题过程,然后解答后面的问题.
如图①,已知AB∥CD,∠B=35°,∠D=32°,求∠BED的度数
(1)如图②,已知∠D=30°,∠ACD=65°,为了保证AB∥DE,∠A应多大?
(2)如图③,要使GP∥HQ,则∠G,∠GFH,∠H之间有什么关系?
解:如图①,过点E作EF∥AB.
则AB∥CD∥EF.因为AB∥EF,所以∠1=∠B=35°.
因为CD∥EF,所以∠2=∠D=32°.所以∠BED=∠1+∠2=35°+32°=67°.
如图②③是明明设计的智力拼图玩具的一部分,现在明明遇到两个问题,请你帮他解决.
解:如图①,过点C作CF∥DE,则∠2=∠D=30°.因为∠ACD=65°,即∠1+∠2=65°,所以∠1=65°-∠2=65°-30°=35°.因为AB∥DE,CF∥DE,所以AB∥CF,所以∠A=∠1=35°.
解:如图②,过点F作FI∥GP,则∠G+∠1=180°.因为GP∥HQ,FI∥GP,所以HQ∥FI.所以∠2+∠H=180°,所以∠G+∠1+∠2+∠H=360°,即∠G+∠GFH+∠H=360°.
23.如图,
AB∥CD,BN,DN分别平分∠ABM,∠MDC,则∠BMD与∠N之间的数量关系如何?请说明理由.
解:∠BMD=2∠N.理由如下:如图,过点M作ME∥AB,则∠ABM=∠BME.
∵AB∥CD,ME∥AB,∴ME∥CD.∴∠CDM=∠DME.∴∠ABM+∠CDM=∠BME+∠DME=∠BMD.
同理∠N=∠ABN+∠CDN.∵BN,DN分别平分∠ABM,∠MDC,
∴∠ABM=2∠ABN,∠CDM=2∠CDN.∴∠ABM+∠CDM=2∠ABN+2∠CDN.∴∠BMD=2∠N.
24.【2020·武汉】如图,直线EF分别与直线AB,CD相交于点E,F.EM平分∠BEF,FN平分∠CFE,且EM∥FN.求证:AB∥CD.
证明:∵EM∥FN,∴∠FEM=∠EFN.又∵EM平分∠BEF,FN平分∠CFE,
∴∠FEB=∠EFC.∴AB∥CD.
如图,已知∠ABC,请你再画一个∠DEF,使DE∥AB,EF∥BC,且DE交BC边于点P.探究:∠ABC与∠DEF有怎样的数量关系?并说明理由.
解:画图如图①②③④所示.∠ABC与∠DEF相等或互补,
理由如下:如图①,∵AB∥DE,∴∠ABC=∠DPC.∵BC∥EF,∴∠DEF=∠DPC.∴∠ABC=∠DEF.
如图②,∵AB∥DE,∴∠ABC=∠EPC.∵BC∥EF,∴∠EPC=∠DEF.∴∠ABC=∠DEF.
如图③,∵AB∥DE,∴∠ABC=∠BPE.∵BC∥EF,∴∠DEF+∠BPE=180°.∴∠ABC+∠DEF=180°.
如图④,∵AB∥DE,∴∠ABC=∠EPC.∵BC∥EF,∴∠EPC+∠DEF=180°.∴∠ABC+∠DEF=180°.
综上可知,∠ABC与∠DEF相等或互补.
1
2
1
