人教版七年级数学 下册 第十章 10.2 直方图 课件(共44张PPT)
文档属性
| 名称 | 人教版七年级数学 下册 第十章 10.2 直方图 课件(共44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 00:00:00 | ||
图片预览









文档简介
(共44张PPT)
温故知新
1.什么是全面调查?
2.什么是抽样调查?
3.抽样调查要注意哪些问题?
我们已经学习了用哪些统计图来描述数据?
条形统计图
扇形统计图
折线统计图
这节课,再来学习另一种常用的描述数据的统计图——直方图.
导入新课
10.2
直
方
图
人教版七年级数学
下册
目标导航
1.明确频数直方图制作的步骤,会绘制频数直方图。
2.能从频数分布表和频数直方图中获取有关信息,作出
合理的判断和预测。
认真阅读课本中10.2
直方图的内容,完成下面练习并体验知识点的形成过程。
自主研学
我们可以这样读书:
点信息,划精要
,圈疑问
一边读一边做标识,
一边读一边做评注,
一边读一边做概括.
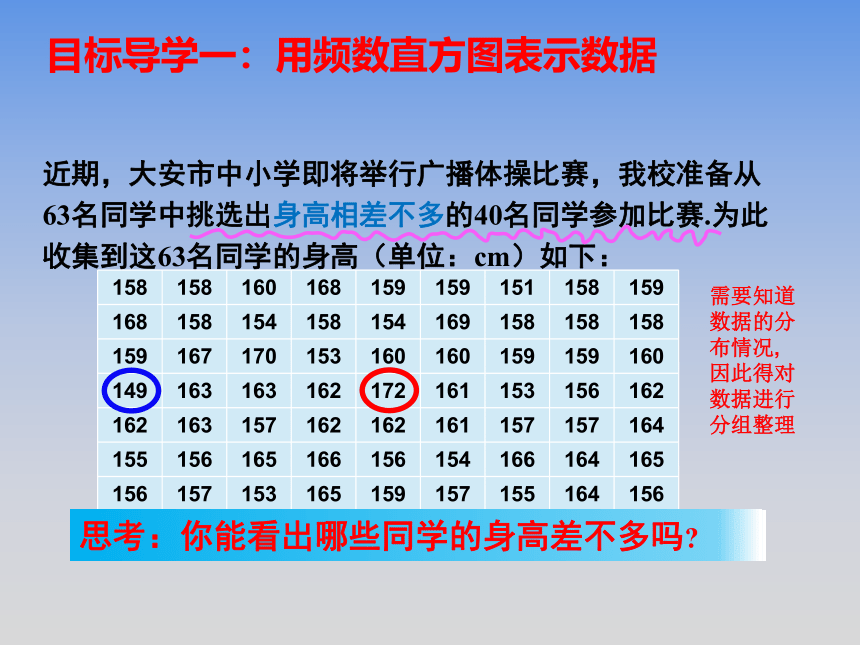
近期,大安市中小学即将举行广播体操比赛,我校准备从63名同学中挑选出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
158
158
160
168
159
159
151
158
159
168
158
154
158
154
169
158
158
158
159
167
170
153
160
160
159
159
160
149
163
163
162
172
161
153
156
162
162
163
157
162
162
161
157
157
164
155
156
165
166
156
154
166
164
165
156
157
153
165
159
157
155
164
156
思考:身高最高的是多少?最矮是多少?相差多少?
思考:这63名学生在哪个范围内变化?
思考:你能看出哪些同学的身高差不多吗?
需要知道数据的分布情况,因此得对数据进行分组整理
目标导学一:用频数直方图表示数据
阅读课本,完成下列问题:
1、什么是组距?
2、什么是组数?
3、什么是频数?
4、如何对数据进行分组整理?分几步?
如何分组整理数据,如何描述数据?
把所有数据分成若干组,每个小组的两个端点之间的距离.
分成的组的个数.
落在各个小组内的数据的个数.
为了使选取的参赛选手身高比较整齐,需要知道数据(身高)的分布情况.为此可以通过对这些数据适当分组来进行整理.
1.计算最大值与最小值的差
2.决定组距和组数
3.列频数分析表
4.画频数分布直方图
在上面的数据中,最小值是149,最大值是172,它们的差是23,说明身高的变化范围是23
cm.
1.计算最大值和最小值的差
2.决定组距和组数
所以要将数据分成8组:149≤x<152,152≤x<155,…,170≤x<173.这里组数和组距分别是8和3.
本问题中我们作等距分组,即令各组的组距相同.如果从最小值起每隔3
cm
作为一个组,那么由于
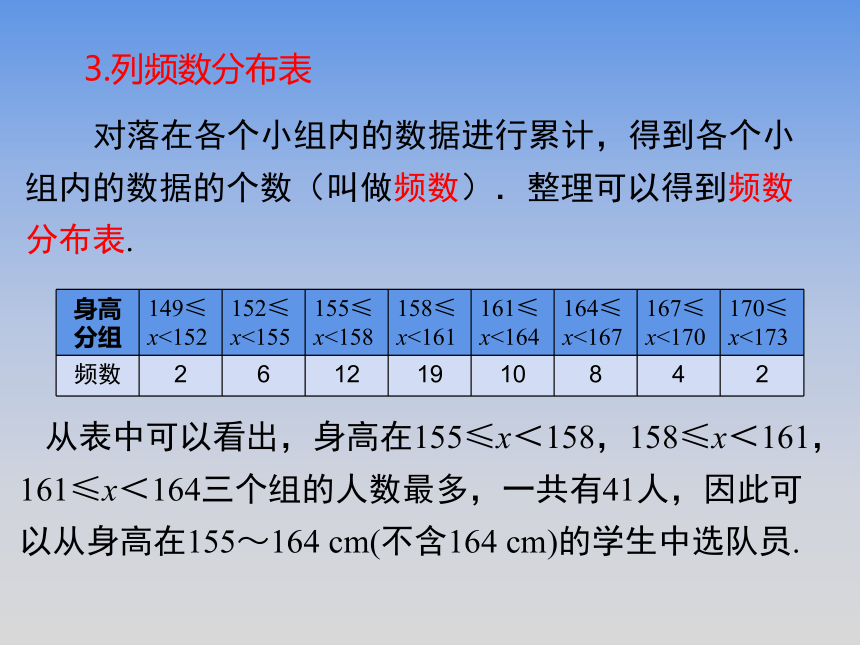
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表.
3.列频数分布表
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有41人,因此可以从身高在155~164
cm(不含164
cm)的学生中选队员.
身高分组
149≤x<152
152≤x<155
155≤x<158
158≤x<161
161≤x<164
164≤x<167
167≤x<170
170≤x<173
频数
2
6
12
19
10
8
4
2
频数分布表有何优点?
答:易于显示大小数据次数多少,分布情况,哪一组数据较集中等。
频数分布表有何不足之处?
答:原始数据不见了,还不够直观.
想一想
上例我们选取的组距是3,从而把数据分成8组,如果我们选取的组距是2或4,那么应分成几个组呢?这样能否选出需要的40名同学呢?
小长方形的高是频数与组距的比值
小长方形的宽是组距
频数/组距
0
149
152
155
158
161
164
167
170
173
1
2
5
6
7
身高/cm
3
4
4.画频数分布直方图
为了更直观形象地看出频数分布的情况,可以根据频数分布表,画出频数分布直方图.
横轴
纵轴
小长方形的面积=组距×(频数÷组距)=频数
绘直方图的方法:
(1)根据图纸的大小,画出两条相互垂直的
射线,两端加上箭头;
(2)在水平射线上,适当分配条形的位置,
确定直条的宽度和间隔;
(3)在与水平射线垂直的射线上,根据数据的
大小情况,确定单位长度的多少,再照根据
大小,画出长短不同的直条并注名数量.
通过对直方图的学习,你能说说条形图与直方图有什么相同与不同吗?
1:条形图各矩形间有空隙,直方图各矩形间无空隙。
条形图与直方图的区别:
2.直方图可以显示各组频数分布情况,而条形图不能反映这一点。
例1
某校一学生社团参加数学实践活动,和交警一起在金山大道入口用移动测速仪监测一组汽车通过的时速(千米/时),在数据整理统计绘制频数直方图的过程中,不小心用墨汁将表中的部分数据污染(见下表),请根据下面不完整的频数分布表和频数直方图,解答问题:(注:50~60指时速大于等于50千米/时而小于60千米/时,其他类同)
精典例题
(1)请用你所学的数学统计知识,补全频数直方图;
39
(2)如果此地汽车时速不低于80千米/时即为违章,求这组汽车的违章频数;
(3)如果请你根据调查数据绘制扇形统计图,那么时速在70~80范围内的车辆数所对应的扇形圆心角的度数是________.
解:18+22=40
144°
例2
某商店将300个营业日的营业额做成直方图,如下图所示,请依图回答下列问题:
(1)营业额不到
30
万元的天数占总营业日天数的多少百分比?
(2)有多少天的营业额不到
30
万元?
(3)有多少天的营业额在
40
万元以上?
精典例题
(1)由上图可知,营业额不到30万元的天数占总营业日天数的百分比是10%+9%+28%=47%.
(2)因为总营业日为300天,所以营业额不到30万元有300×47%=141(天).
(3)营业额在40万元以上的占12%+6%+1%=19%,所以有
300×19%=57
(天).
130
135
140
145
150
155
160
165
170
脉搏次数
(次/分)
频数(学生人数)
1.根据直方图回答问题:
(1)脉搏在
范围的学生最多,有
个人。
(2)脉搏在135~140有
人,160~165有
人,
(3)
全班有
人。
155~160
14
2
11
49
即学即练
例3:为了考察某种大麦穗长的分布情况,在一块实验田里抽取了100个麦穗,量得它们的长度如下表(单位:cm)
6.5
6.4
6.7
5.8
5.9
5.9
5.2
4.0
5.4
4.6
5.8
5.5
6.0
6.5
5.1
6.5
5.3
5.9
5.5
5.8
6.2
5.4
5.0
5.0
6.8
6.0
5.0
5.7
6.0
5.5
6.8
6.0
6.3
5.5
5.0
6.3
5.2
6.0
7.0
6.4
6.4
5.8
5.9
5.7
6.8
6.6
6.0
6.4
7.0
6.4
6.0
5.4
6.5
6.0
6.8
5.8
6.3
6.0
6.3
5.6
5.3
6.4
5.7
6.7
6.2
5.6
6.0
6.7
6.7
6.0
5.5
6.2
6.1
5.3
6.2
6.8
6.6
4.7
5.7
5.7
5.8
5.3
7.0
6.0
6.0
5.9
5.4
6.0
5.2
6.0
6.3
5.7
6.8
6.1
4.5
5.6
6.3
6.0
5.8
6.3
列出样本的频数分布表,画出频数分布直方图。
目标导学二:制作频数直方图
列出样本的频数分布表,画出频数分布直方图,从图表中可以得到什么信息?
解:(1)计算最大值和最小值的差
在样本数据中,最大值是7.4,最小值是4.0,它们的差是
7.4-4.0=3.4(cm)
(2)决定组距和组数
最大值与最小值的差是3.4
cm,若取组距为0.3
cm,那么由于
注意:一般情况
(1)可以由组距来求组数;
(2)当数据个数小于40时,组数为6-8组;
当数据个数40—100个时,组数为7-10组;
可以分成12组,组数合适,于是取组距为0.3
cm,组数为12.
分组
划记
频数
一
1
一
1
2
正
5
正正一
11
正正正
15
正正正正正
28
正正
13
正正一
11
正正
10
2
一
1
合计
100
(3)列频数分布表
(4)
画频数分布直方图
从表和图中可以看出,麦穗长度大部分落在5.2
cm至7.0
cm之间,其他区域较少.长度在5.8≤x<6.1范围内的麦穗个数最多,有28个,而长度在4.0≤x<4.3,4.3≤x<4.6,
4.6≤x<4.9,
7.0≤x<7.3,
7.3≤x<7.6范围内的麦穗个数很少,总共有7个.
某班一次数学竞赛成绩(单位:分)如下:
77,74,65,53,95,87,75,82,71,67,85,88,90,86,81,87,70,70,89,69,61,94,79,81,76,67,80,63,84,91,53,69,81,61,69,91,78,75,81,87.
(1)将数据适当分组,并绘制相应的频数分布直方图;
(2)从统计图中你能得到什么信息?
即学即练
解析:(1)先将成绩按10分的距离分段,统计出每个分数段学生出现的频数,如右表:根据右表绘制直方图,如图所示:
成绩x(分)
划记
频数
50≤x<60
丅
2
60≤x<70
正
9
70≤x<80
正正
10
80≤x<90
正正
14
90≤x<100
正
5
点评:画直方图要注意以下几步:①计算极值;②决定组距和组数;③列频数分布表;④画频数分布直方图.
(2)从图中可以清楚地看出80分到90分这个分数段的学生数最多,90分以上的同学较少,60分以下的学生最少.
画频数分布直方图的一般步骤:
(1)
计算最大值与最小值的差(极差).
极差:
(2)
决定组距与组数:
极差/组距=________
数据分成_____组.
(4)列频数分布表.
数出每一组频数
(5)绘制频数分布直方图.
横轴表示各组数据,纵轴表示频数,
该组内的频数为高,画出一个个矩形。
(3)
决定分点.
注意:一般情况
(1)可以由组距来求组数;
(2)当数据个数小于40时,组数为6-8组;
当数据个数40—100个时,组数为7-10组;
课堂小结
检测目标
2.已知样本10,
8,
6,
10,
8,13,11,10,
12,7,8,9,12,9,11,12,9,10,11,
11,
那么
频率为0.2范围的是
(
)
A.
5.5~7.5
B.
7.5~9.5
C.
9.5~11.5
D.
11.5~13.5
分组
频数
频率
5.5~7.5
2
0.1
7.5~9.5
6
0.3
9.5~11.5
8
0.4
11.5~13.5
4
0.2
合计
20
1.0
D
检测目标
3.为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘成如图所示的频数分布直方图,已知该校共有1
000名学生.据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
A.280
B.240
C.300
D.260
A
检测目标
4.如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1∶4∶3∶2,那么该班一分钟跳绳次数在100次以上的学生有(
)
A.6人
B.8人
C.16人
D.20人
D
检测目标
5.在对七年级某班的一次数学测验成绩进行统计分
析中,各分数段的人数如图所示(分数取正整数,满分100分),请观察图形,并回答下列问题。
(1)该班有
名学生;
(2)70.5~80.5这一组的频数是
,频率是
;
44
14
0.32
人数
分数
50.5
60.5
70.5
80.5
90.5
100.5
检测目标
根据以上信息解决下列问题:
(3)补全条形统计图.
(4)扇形统计图中“C组”所对应的圆心角的度数是_________.
(5)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次听写比赛不合格的学生人数.
6.某校举行英语“单词听写”比赛,每位学生听写英语单词
39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果
绘制的统计图的一部分.
(1)该次随机抽查的学生总人数是______.
(2)在统计表中,m=_____,n=_____.
60
50
40
30
20
10
检测目标
7.下面数据是截至2010年费尔兹奖得主获奖时的年龄:
29????39????35????33????39????28????33????35????
31????31????37????32???
38????36????31????39????
32????38????37????34????29????34????38????32
35????36????33????29????32????35????36????37???
39????38????40????38??
?37????39????38????34????
33????40????36????36????37????40????31????38
38???
40???
40???
37
请根据下面不同的分组方法列出频数分布表,画出频数分布直方图,比较哪一种分组能更好地说明费尔兹奖得主获奖时的年龄分布:
(1)组距是2,各组是28≤x<30,30≤x<32,…;
(2)组距是5,各组是25≤x<30,30≤x<35,…;
(3)组距是10,各组是20≤x<30,30≤x<40,….
检测目标
解:(1)根据题意列表如下:
(2)列表如下:
(3)列表如下:
选(2)组能更好地说明费尔兹奖得主获奖时的年龄分布;
第(1)组,组距太小,操作麻烦;
第(3)组,组距太大,不能很好地说明问题.
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
温故知新
1.什么是全面调查?
2.什么是抽样调查?
3.抽样调查要注意哪些问题?
我们已经学习了用哪些统计图来描述数据?
条形统计图
扇形统计图
折线统计图
这节课,再来学习另一种常用的描述数据的统计图——直方图.
导入新课
10.2
直
方
图
人教版七年级数学
下册
目标导航
1.明确频数直方图制作的步骤,会绘制频数直方图。
2.能从频数分布表和频数直方图中获取有关信息,作出
合理的判断和预测。
认真阅读课本中10.2
直方图的内容,完成下面练习并体验知识点的形成过程。
自主研学
我们可以这样读书:
点信息,划精要
,圈疑问
一边读一边做标识,
一边读一边做评注,
一边读一边做概括.
近期,大安市中小学即将举行广播体操比赛,我校准备从63名同学中挑选出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
158
158
160
168
159
159
151
158
159
168
158
154
158
154
169
158
158
158
159
167
170
153
160
160
159
159
160
149
163
163
162
172
161
153
156
162
162
163
157
162
162
161
157
157
164
155
156
165
166
156
154
166
164
165
156
157
153
165
159
157
155
164
156
思考:身高最高的是多少?最矮是多少?相差多少?
思考:这63名学生在哪个范围内变化?
思考:你能看出哪些同学的身高差不多吗?
需要知道数据的分布情况,因此得对数据进行分组整理
目标导学一:用频数直方图表示数据
阅读课本,完成下列问题:
1、什么是组距?
2、什么是组数?
3、什么是频数?
4、如何对数据进行分组整理?分几步?
如何分组整理数据,如何描述数据?
把所有数据分成若干组,每个小组的两个端点之间的距离.
分成的组的个数.
落在各个小组内的数据的个数.
为了使选取的参赛选手身高比较整齐,需要知道数据(身高)的分布情况.为此可以通过对这些数据适当分组来进行整理.
1.计算最大值与最小值的差
2.决定组距和组数
3.列频数分析表
4.画频数分布直方图
在上面的数据中,最小值是149,最大值是172,它们的差是23,说明身高的变化范围是23
cm.
1.计算最大值和最小值的差
2.决定组距和组数
所以要将数据分成8组:149≤x<152,152≤x<155,…,170≤x<173.这里组数和组距分别是8和3.
本问题中我们作等距分组,即令各组的组距相同.如果从最小值起每隔3
cm
作为一个组,那么由于
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表.
3.列频数分布表
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有41人,因此可以从身高在155~164
cm(不含164
cm)的学生中选队员.
身高分组
149≤x<152
152≤x<155
155≤x<158
158≤x<161
161≤x<164
164≤x<167
167≤x<170
170≤x<173
频数
2
6
12
19
10
8
4
2
频数分布表有何优点?
答:易于显示大小数据次数多少,分布情况,哪一组数据较集中等。
频数分布表有何不足之处?
答:原始数据不见了,还不够直观.
想一想
上例我们选取的组距是3,从而把数据分成8组,如果我们选取的组距是2或4,那么应分成几个组呢?这样能否选出需要的40名同学呢?
小长方形的高是频数与组距的比值
小长方形的宽是组距
频数/组距
0
149
152
155
158
161
164
167
170
173
1
2
5
6
7
身高/cm
3
4
4.画频数分布直方图
为了更直观形象地看出频数分布的情况,可以根据频数分布表,画出频数分布直方图.
横轴
纵轴
小长方形的面积=组距×(频数÷组距)=频数
绘直方图的方法:
(1)根据图纸的大小,画出两条相互垂直的
射线,两端加上箭头;
(2)在水平射线上,适当分配条形的位置,
确定直条的宽度和间隔;
(3)在与水平射线垂直的射线上,根据数据的
大小情况,确定单位长度的多少,再照根据
大小,画出长短不同的直条并注名数量.
通过对直方图的学习,你能说说条形图与直方图有什么相同与不同吗?
1:条形图各矩形间有空隙,直方图各矩形间无空隙。
条形图与直方图的区别:
2.直方图可以显示各组频数分布情况,而条形图不能反映这一点。
例1
某校一学生社团参加数学实践活动,和交警一起在金山大道入口用移动测速仪监测一组汽车通过的时速(千米/时),在数据整理统计绘制频数直方图的过程中,不小心用墨汁将表中的部分数据污染(见下表),请根据下面不完整的频数分布表和频数直方图,解答问题:(注:50~60指时速大于等于50千米/时而小于60千米/时,其他类同)
精典例题
(1)请用你所学的数学统计知识,补全频数直方图;
39
(2)如果此地汽车时速不低于80千米/时即为违章,求这组汽车的违章频数;
(3)如果请你根据调查数据绘制扇形统计图,那么时速在70~80范围内的车辆数所对应的扇形圆心角的度数是________.
解:18+22=40
144°
例2
某商店将300个营业日的营业额做成直方图,如下图所示,请依图回答下列问题:
(1)营业额不到
30
万元的天数占总营业日天数的多少百分比?
(2)有多少天的营业额不到
30
万元?
(3)有多少天的营业额在
40
万元以上?
精典例题
(1)由上图可知,营业额不到30万元的天数占总营业日天数的百分比是10%+9%+28%=47%.
(2)因为总营业日为300天,所以营业额不到30万元有300×47%=141(天).
(3)营业额在40万元以上的占12%+6%+1%=19%,所以有
300×19%=57
(天).
130
135
140
145
150
155
160
165
170
脉搏次数
(次/分)
频数(学生人数)
1.根据直方图回答问题:
(1)脉搏在
范围的学生最多,有
个人。
(2)脉搏在135~140有
人,160~165有
人,
(3)
全班有
人。
155~160
14
2
11
49
即学即练
例3:为了考察某种大麦穗长的分布情况,在一块实验田里抽取了100个麦穗,量得它们的长度如下表(单位:cm)
6.5
6.4
6.7
5.8
5.9
5.9
5.2
4.0
5.4
4.6
5.8
5.5
6.0
6.5
5.1
6.5
5.3
5.9
5.5
5.8
6.2
5.4
5.0
5.0
6.8
6.0
5.0
5.7
6.0
5.5
6.8
6.0
6.3
5.5
5.0
6.3
5.2
6.0
7.0
6.4
6.4
5.8
5.9
5.7
6.8
6.6
6.0
6.4
7.0
6.4
6.0
5.4
6.5
6.0
6.8
5.8
6.3
6.0
6.3
5.6
5.3
6.4
5.7
6.7
6.2
5.6
6.0
6.7
6.7
6.0
5.5
6.2
6.1
5.3
6.2
6.8
6.6
4.7
5.7
5.7
5.8
5.3
7.0
6.0
6.0
5.9
5.4
6.0
5.2
6.0
6.3
5.7
6.8
6.1
4.5
5.6
6.3
6.0
5.8
6.3
列出样本的频数分布表,画出频数分布直方图。
目标导学二:制作频数直方图
列出样本的频数分布表,画出频数分布直方图,从图表中可以得到什么信息?
解:(1)计算最大值和最小值的差
在样本数据中,最大值是7.4,最小值是4.0,它们的差是
7.4-4.0=3.4(cm)
(2)决定组距和组数
最大值与最小值的差是3.4
cm,若取组距为0.3
cm,那么由于
注意:一般情况
(1)可以由组距来求组数;
(2)当数据个数小于40时,组数为6-8组;
当数据个数40—100个时,组数为7-10组;
可以分成12组,组数合适,于是取组距为0.3
cm,组数为12.
分组
划记
频数
一
1
一
1
2
正
5
正正一
11
正正正
15
正正正正正
28
正正
13
正正一
11
正正
10
2
一
1
合计
100
(3)列频数分布表
(4)
画频数分布直方图
从表和图中可以看出,麦穗长度大部分落在5.2
cm至7.0
cm之间,其他区域较少.长度在5.8≤x<6.1范围内的麦穗个数最多,有28个,而长度在4.0≤x<4.3,4.3≤x<4.6,
4.6≤x<4.9,
7.0≤x<7.3,
7.3≤x<7.6范围内的麦穗个数很少,总共有7个.
某班一次数学竞赛成绩(单位:分)如下:
77,74,65,53,95,87,75,82,71,67,85,88,90,86,81,87,70,70,89,69,61,94,79,81,76,67,80,63,84,91,53,69,81,61,69,91,78,75,81,87.
(1)将数据适当分组,并绘制相应的频数分布直方图;
(2)从统计图中你能得到什么信息?
即学即练
解析:(1)先将成绩按10分的距离分段,统计出每个分数段学生出现的频数,如右表:根据右表绘制直方图,如图所示:
成绩x(分)
划记
频数
50≤x<60
丅
2
60≤x<70
正
9
70≤x<80
正正
10
80≤x<90
正正
14
90≤x<100
正
5
点评:画直方图要注意以下几步:①计算极值;②决定组距和组数;③列频数分布表;④画频数分布直方图.
(2)从图中可以清楚地看出80分到90分这个分数段的学生数最多,90分以上的同学较少,60分以下的学生最少.
画频数分布直方图的一般步骤:
(1)
计算最大值与最小值的差(极差).
极差:
(2)
决定组距与组数:
极差/组距=________
数据分成_____组.
(4)列频数分布表.
数出每一组频数
(5)绘制频数分布直方图.
横轴表示各组数据,纵轴表示频数,
该组内的频数为高,画出一个个矩形。
(3)
决定分点.
注意:一般情况
(1)可以由组距来求组数;
(2)当数据个数小于40时,组数为6-8组;
当数据个数40—100个时,组数为7-10组;
课堂小结
检测目标
2.已知样本10,
8,
6,
10,
8,13,11,10,
12,7,8,9,12,9,11,12,9,10,11,
11,
那么
频率为0.2范围的是
(
)
A.
5.5~7.5
B.
7.5~9.5
C.
9.5~11.5
D.
11.5~13.5
分组
频数
频率
5.5~7.5
2
0.1
7.5~9.5
6
0.3
9.5~11.5
8
0.4
11.5~13.5
4
0.2
合计
20
1.0
D
检测目标
3.为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘成如图所示的频数分布直方图,已知该校共有1
000名学生.据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
A.280
B.240
C.300
D.260
A
检测目标
4.如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1∶4∶3∶2,那么该班一分钟跳绳次数在100次以上的学生有(
)
A.6人
B.8人
C.16人
D.20人
D
检测目标
5.在对七年级某班的一次数学测验成绩进行统计分
析中,各分数段的人数如图所示(分数取正整数,满分100分),请观察图形,并回答下列问题。
(1)该班有
名学生;
(2)70.5~80.5这一组的频数是
,频率是
;
44
14
0.32
人数
分数
50.5
60.5
70.5
80.5
90.5
100.5
检测目标
根据以上信息解决下列问题:
(3)补全条形统计图.
(4)扇形统计图中“C组”所对应的圆心角的度数是_________.
(5)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次听写比赛不合格的学生人数.
6.某校举行英语“单词听写”比赛,每位学生听写英语单词
39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果
绘制的统计图的一部分.
(1)该次随机抽查的学生总人数是______.
(2)在统计表中,m=_____,n=_____.
60
50
40
30
20
10
检测目标
7.下面数据是截至2010年费尔兹奖得主获奖时的年龄:
29????39????35????33????39????28????33????35????
31????31????37????32???
38????36????31????39????
32????38????37????34????29????34????38????32
35????36????33????29????32????35????36????37???
39????38????40????38??
?37????39????38????34????
33????40????36????36????37????40????31????38
38???
40???
40???
37
请根据下面不同的分组方法列出频数分布表,画出频数分布直方图,比较哪一种分组能更好地说明费尔兹奖得主获奖时的年龄分布:
(1)组距是2,各组是28≤x<30,30≤x<32,…;
(2)组距是5,各组是25≤x<30,30≤x<35,…;
(3)组距是10,各组是20≤x<30,30≤x<40,….
检测目标
解:(1)根据题意列表如下:
(2)列表如下:
(3)列表如下:
选(2)组能更好地说明费尔兹奖得主获奖时的年龄分布;
第(1)组,组距太小,操作麻烦;
第(3)组,组距太大,不能很好地说明问题.
课堂总结
同学们,本节课你收获了什么?
课后作业
1.整理本节知识点
2.选做题:
同步检测题
