2.2.2平均数、众数、中位数(18张PPT)
文档属性
| 名称 | 2.2.2平均数、众数、中位数(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 461.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 20:29:36 | ||
图片预览






文档简介
众数、中位数、平均数
高中数学必修3第二章2.2.2
用样本的数字特征估计总体的数字特征(1)
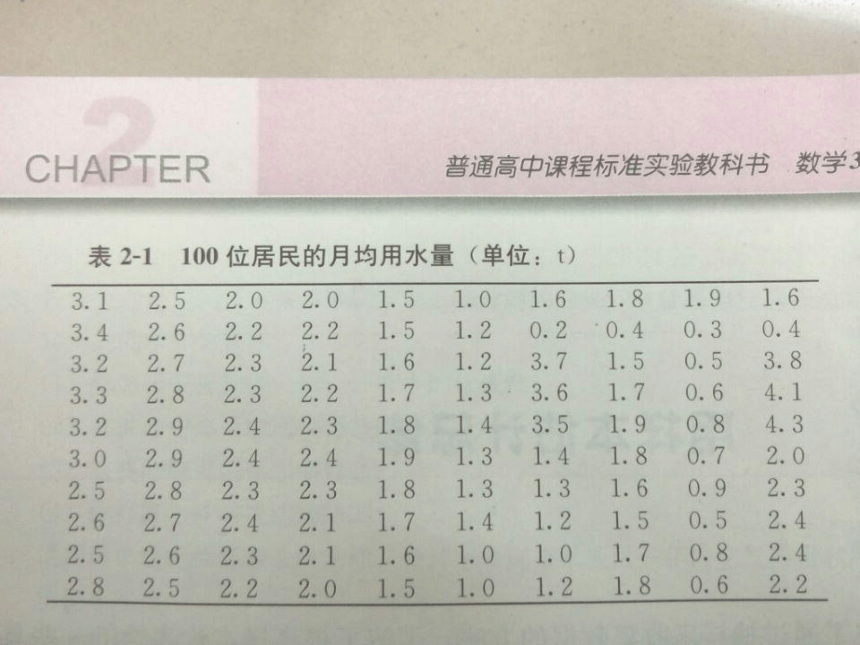
必修3P72:100位居民的月均用水量(单位:t)
月均用水量
/
t
频率
/
组距
o
4
.
5
4
3
.
5
3
2
.
5
2
1
.
5
1
0
.
5
0
.
5
0
.
4
0
.
3
0
.
2
0
.
1
0.04
0.08
0.15
0.22
0.25
0.05
0.04
0.02
0.15
3.所有矩形面积之和为1.
2.各区间矩形面积表示频率
1.纵轴表示:
频率
组距
样本估计总体的两种方案
A:样本频率分布表
直方图(折线图,密度曲线)
B: 茎叶图
数据保存完整,但容量不宜较大
直观反映总体的分布
平均数
据估计:浙江省嵊州市谷来镇马溪村财富约有360亿美元,人口1200人,人均财富多少呢?用平均数估计该村的富裕程度科学吗?
中位数
数据按大小排列,最中间位置的数(或两个数据的平均数)叫做这组数据的中位数。
平均数
平均数
平均数与每一个样本的数据有关,反映样本数据全体的信息,但平均数受数据中的极端值的影响较大,有时使平均数在估计总体时可靠性降低。
2.中位数
将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数。
1平均数
3. 众 数
在一组数据中,出现次数最多的
数据叫做这一组数据的众数。
例如有人问:高二同学的年龄是多少呢
众数、中位数和平均数的对比
众数
1.容易通过计算得到。
2.不容易受数据中极端数值的影响。
平均数
1.需全组所有数据来计算。
2.受数据中极端数值的影响。
中位数
1.仅需按序排列,无计算
2.不受极端值影响
特征数就是把一组数据汇总简化成一个数值来代表,也可以理解为“中心点”
探究1:如何从频率分布直方图中估计众数?
众数在样本频率分布直方图中,就是最高矩形中点的横坐标。
月均用水量
/
t
频率
/
组距
o
4
.
5
4
3
.
5
3
2
.
5
2
1
.
5
1
0
.
5
0
.
5
0
.
4
0
.
3
0
.
2
0
.
1
0.04
0.08
0.15
0.22
0.25
0.05
0.04
0.02
0.15
2.25
月均用水量
/
t
频率
/
组距
o
4
.
5
4
3
.
5
3
2
.
5
2
1
.
5
1
0
.
5
0
.
5
0
.
4
0
.
3
0
.
2
0
.
1
0.04
0.08
0.15
0.22
0.25
0.05
0.04
0.02
0.15
探究2:如何从频率分布直方图中估计中位数?
总结:用分界线把直方图分成左右面积相等,分界线的横坐标估计为中位数。
注:图中的数据是小矩形的面积
即频率
上图中,设中位数为x,则
前四个小矩形的面积和=0.49
2.02
探究3:如何从频率分布直方图中估计平均数?
结论:平均数等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。
思考:频率分布直方图中估计的众数与原始数据中的众数是否会有不同,为什么?
在频率分布直方图,我们只能直观地看出数据的大概分布情况,从直方图本身得不出原始数据的每一个值,可以说已经损失一些样本的具体信息。
众数:直方图中面积最高矩形 “中点”的横坐标
中位数:左右两边直方图的面积相等.
平均数:频率分布直方图中每个小矩形的面积乘以小矩 形底边中点的横坐标之和.
用直方图估计三个特征数的要点
练习1:某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果分成5组:
下图为按上述分组得到的频率分布直方图:
(1)估计该班学生百米测试成绩的众数
(2)估计该班学生百米测试成绩的中位数
(3)估计该班学生百米测试成绩的平均数
练习2:(2012·高考)某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)根据频率分布直方图,
估计这100名学生语文成绩
的平均分;
众数:直方图中面积最高矩形 “中点”的横坐标
中位数:左右两边直方图的面积相等.
平均数:频率分布直方图中每个小矩形的面积乘以小矩 形底边中点的横坐标之和.
用直方图估计三个特征数的要点
五、课外作业:课外诊断练习卷
谢谢,再见
高中数学必修3第二章2.2.2
用样本的数字特征估计总体的数字特征(1)
必修3P72:100位居民的月均用水量(单位:t)
月均用水量
/
t
频率
/
组距
o
4
.
5
4
3
.
5
3
2
.
5
2
1
.
5
1
0
.
5
0
.
5
0
.
4
0
.
3
0
.
2
0
.
1
0.04
0.08
0.15
0.22
0.25
0.05
0.04
0.02
0.15
3.所有矩形面积之和为1.
2.各区间矩形面积表示频率
1.纵轴表示:
频率
组距
样本估计总体的两种方案
A:样本频率分布表
直方图(折线图,密度曲线)
B: 茎叶图
数据保存完整,但容量不宜较大
直观反映总体的分布
平均数
据估计:浙江省嵊州市谷来镇马溪村财富约有360亿美元,人口1200人,人均财富多少呢?用平均数估计该村的富裕程度科学吗?
中位数
数据按大小排列,最中间位置的数(或两个数据的平均数)叫做这组数据的中位数。
平均数
平均数
平均数与每一个样本的数据有关,反映样本数据全体的信息,但平均数受数据中的极端值的影响较大,有时使平均数在估计总体时可靠性降低。
2.中位数
将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数。
1平均数
3. 众 数
在一组数据中,出现次数最多的
数据叫做这一组数据的众数。
例如有人问:高二同学的年龄是多少呢
众数、中位数和平均数的对比
众数
1.容易通过计算得到。
2.不容易受数据中极端数值的影响。
平均数
1.需全组所有数据来计算。
2.受数据中极端数值的影响。
中位数
1.仅需按序排列,无计算
2.不受极端值影响
特征数就是把一组数据汇总简化成一个数值来代表,也可以理解为“中心点”
探究1:如何从频率分布直方图中估计众数?
众数在样本频率分布直方图中,就是最高矩形中点的横坐标。
月均用水量
/
t
频率
/
组距
o
4
.
5
4
3
.
5
3
2
.
5
2
1
.
5
1
0
.
5
0
.
5
0
.
4
0
.
3
0
.
2
0
.
1
0.04
0.08
0.15
0.22
0.25
0.05
0.04
0.02
0.15
2.25
月均用水量
/
t
频率
/
组距
o
4
.
5
4
3
.
5
3
2
.
5
2
1
.
5
1
0
.
5
0
.
5
0
.
4
0
.
3
0
.
2
0
.
1
0.04
0.08
0.15
0.22
0.25
0.05
0.04
0.02
0.15
探究2:如何从频率分布直方图中估计中位数?
总结:用分界线把直方图分成左右面积相等,分界线的横坐标估计为中位数。
注:图中的数据是小矩形的面积
即频率
上图中,设中位数为x,则
前四个小矩形的面积和=0.49
2.02
探究3:如何从频率分布直方图中估计平均数?
结论:平均数等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。
思考:频率分布直方图中估计的众数与原始数据中的众数是否会有不同,为什么?
在频率分布直方图,我们只能直观地看出数据的大概分布情况,从直方图本身得不出原始数据的每一个值,可以说已经损失一些样本的具体信息。
众数:直方图中面积最高矩形 “中点”的横坐标
中位数:左右两边直方图的面积相等.
平均数:频率分布直方图中每个小矩形的面积乘以小矩 形底边中点的横坐标之和.
用直方图估计三个特征数的要点
练习1:某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果分成5组:
下图为按上述分组得到的频率分布直方图:
(1)估计该班学生百米测试成绩的众数
(2)估计该班学生百米测试成绩的中位数
(3)估计该班学生百米测试成绩的平均数
练习2:(2012·高考)某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)根据频率分布直方图,
估计这100名学生语文成绩
的平均分;
众数:直方图中面积最高矩形 “中点”的横坐标
中位数:左右两边直方图的面积相等.
平均数:频率分布直方图中每个小矩形的面积乘以小矩 形底边中点的横坐标之和.
用直方图估计三个特征数的要点
五、课外作业:课外诊断练习卷
谢谢,再见
