高一数学必修3第二章统计单元测试 Word含答案
文档属性
| 名称 | 高一数学必修3第二章统计单元测试 Word含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 468.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 20:43:47 | ||
图片预览


文档简介
《统计》单元测试
一、选择题
1.某学校为了了解高一年级学生对教师教学的意见,打算从高一年级2007名学生中抽取50名进行抽查,若采用下面的方法选取:先用简单随机抽样从2007人中剔除7人,剩下2000人再按系统抽样的方法进行,则每人入选的机会( )
A. 不全相等 B. 均不相等 C. 都相等 D. 无法确定
2.有20位同学,编号从1至20,现在从中抽取4人作问卷调查,用系统抽样方法确定所抽的编号为(?? )
A.5,10,15,20???? B.2,6,10,14 C.2,4,6,8????? D.5,8,11,14
3.某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为(1);在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为(2)。则完成(1)、(2)这两项调查宜采用的抽样方法依次是( )
A.分层抽样法,系统抽样法 B.分层抽样法,简单随机抽样法
C.系统抽样法,分层抽样法 D.简单随机抽样法,分层抽样法
4.已知两组样本数据的平均数为h,的平均数为k, 则把两组数据合并成一组以后,这组样本的平均数为( )
A. B. C. D.
5.下列说法中,正确的个数是( )
(1) 在频率分布直方图中,中位数左边和右边的直方图的面积相等。
(2)平均数是频率分布直方图的“重心”。
(3) 如果一组数中每个数减去同一个非零常数,则这一组数的平均数改变,方差不改变。
(4)一个样本的方差s2= [(x一3)2+-(X—3) 2+…+(X一3) 2],则这组数据等总和等于60.
(5) 数据的方差为,则数据的方差为
A. 5 B. 4 C.3 D. 2
6.在下列各图中,每个图的两个变量具有相关关系的图是( )
(1) (2) (3) (4)
A.(1)(2) B.(1)(3) C.(2)(4) D.(2)(3)
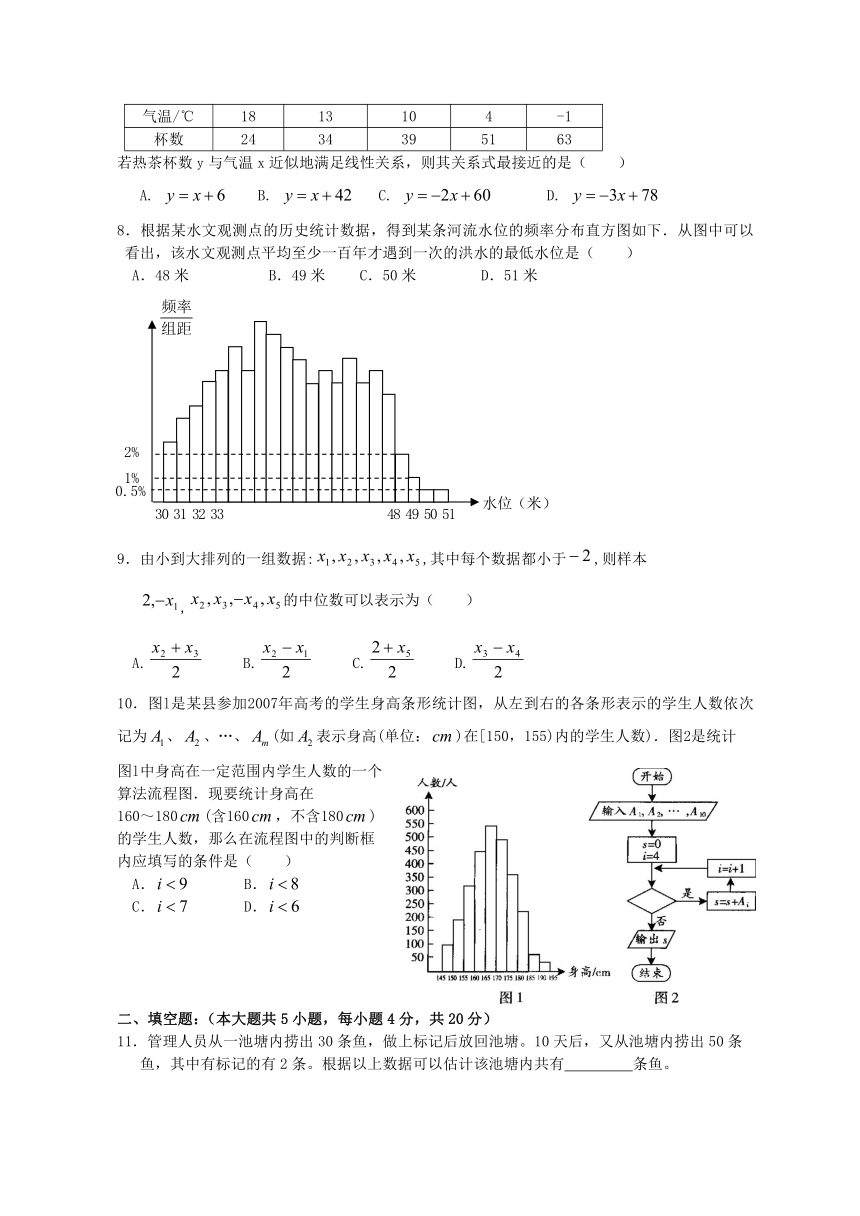
7. 下表是某小卖部一周卖出热茶的杯数与当天气温的对比表:
气温/℃ 18 13 10 4 -1
杯数 24 34 39 51 63
若热茶杯数y与气温x近似地满足线性关系,则其关系式最接近的是( )
A. B. C. D.
8.根据某水文观测点的历史统计数据,得到某条河流水位的频率分布直方图如下.从图中可以看出,该水文观测点平均至少一百年才遇到一次的洪水的最低水位是( )
A.48米 B.49米 C.50米 D.51米
9.由小到大排列的一组数据:,其中每个数据都小于,则样本
,的中位数可以表示为( )
A. B. C. D.
10.图l是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为、、…、(如表示身高(单位:)在[150,155)内的学生人数).图2是统计
图l中身高在一定范围内学生人数的一个
算法流程图.现要统计身高在
160~180(含160,不含180)
的学生人数,那么在流程图中的判断框
内应填写的条件是( )
A. B.
C. D.
二、填空题:(本大题共5小题,每小题4分,共20分)
11.管理人员从一池塘内捞出30条鱼,做上标记后放回池塘。10天后,又从池塘内捞出50条
鱼,其中有标记的有2条。根据以上数据可以估计该池塘内共有 条鱼。
12.某校高中部有三个年级,其中高三有学生1000人,现采用分层抽样法抽取一个容量为185的样本,已知在高一年级抽取了75人,高二年级抽取了60人,则高中部共有__ __学生。
13 已知辆汽车通过某一段公路时的时速
的频率分布直方图如右图所示,则时速在
的汽车大约有_________辆.
14.已知与之间的一组数据为
0 1 2 3
1 3 5-a 7+a
则与的回归直线方程必过定点______
15. 已知样本的平均数是,标准差是,则
三、解答题
16.在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)
3
4
5
62.5344.5
3 2.5
4 3
5 4
6 4.50
0
0
00000
分组 频数
合计
共有100个数据,将数据分组如右表:
(1)画出频率分布表,并画出频率分布直方图;
(2)估计纤度落在中的概率及纤度小于的概率是
多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
17.在2007全运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲,乙两个成绩;并根据茎叶图分析甲、乙两人成绩;
(2)分别计算两个样本的平均数和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定。
18.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗(吨)标准煤的几组对照数据:
3 4 5 6
2.5 3 4 4.5
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式 ,)
《统计》单元测试参考答案
一、选择题: CABBA, DCCCB
二、填空题:11、750 12、3700 13、80 14、 15、96
三、解答题:
16.(Ⅰ)
分组 频数 频率
4 0.04
25 0.25
30 0.30
29 0.29
10 0.10
2 0.02
合计 100 1.00
(2)纤度落在中的概率约为,
纤度小于1.40的概率约为.
(Ⅲ)总体数据的众数:1.40 中位数:1.408
平均数:
.
17.(1)如图所示,茎表示成绩的整数环数,叶表示小数点后的数字。
由上图知,甲中位数是9.05,乙中位数是9.15,乙的成绩大致对称,
可以看出乙发挥稳定性好,甲波动性大。
(2)解:(3)甲=×(9.4+8.7+7.5+8.4+10.1+10.5+10.7+7.2+7.8+10.8)=9.11
S甲==1.3
乙=×(9.1+8.7+7.1+9.8+9.7+8.5+10.1+9.2+10.1+9.1)=9.14
S乙==0.9
由S甲>S乙,这说明了甲运动员的波动大于乙运动员的波动,所以我们估计,乙运动员比较稳定。
18.(1)散点图如下
(2)
;
所求的回归方程为
(3) 时, (吨)
预测生产100吨甲产品的生产能耗比技改前降低(吨)
一、选择题
1.某学校为了了解高一年级学生对教师教学的意见,打算从高一年级2007名学生中抽取50名进行抽查,若采用下面的方法选取:先用简单随机抽样从2007人中剔除7人,剩下2000人再按系统抽样的方法进行,则每人入选的机会( )
A. 不全相等 B. 均不相等 C. 都相等 D. 无法确定
2.有20位同学,编号从1至20,现在从中抽取4人作问卷调查,用系统抽样方法确定所抽的编号为(?? )
A.5,10,15,20???? B.2,6,10,14 C.2,4,6,8????? D.5,8,11,14
3.某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为(1);在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为(2)。则完成(1)、(2)这两项调查宜采用的抽样方法依次是( )
A.分层抽样法,系统抽样法 B.分层抽样法,简单随机抽样法
C.系统抽样法,分层抽样法 D.简单随机抽样法,分层抽样法
4.已知两组样本数据的平均数为h,的平均数为k, 则把两组数据合并成一组以后,这组样本的平均数为( )
A. B. C. D.
5.下列说法中,正确的个数是( )
(1) 在频率分布直方图中,中位数左边和右边的直方图的面积相等。
(2)平均数是频率分布直方图的“重心”。
(3) 如果一组数中每个数减去同一个非零常数,则这一组数的平均数改变,方差不改变。
(4)一个样本的方差s2= [(x一3)2+-(X—3) 2+…+(X一3) 2],则这组数据等总和等于60.
(5) 数据的方差为,则数据的方差为
A. 5 B. 4 C.3 D. 2
6.在下列各图中,每个图的两个变量具有相关关系的图是( )
(1) (2) (3) (4)
A.(1)(2) B.(1)(3) C.(2)(4) D.(2)(3)
7. 下表是某小卖部一周卖出热茶的杯数与当天气温的对比表:
气温/℃ 18 13 10 4 -1
杯数 24 34 39 51 63
若热茶杯数y与气温x近似地满足线性关系,则其关系式最接近的是( )
A. B. C. D.
8.根据某水文观测点的历史统计数据,得到某条河流水位的频率分布直方图如下.从图中可以看出,该水文观测点平均至少一百年才遇到一次的洪水的最低水位是( )
A.48米 B.49米 C.50米 D.51米
9.由小到大排列的一组数据:,其中每个数据都小于,则样本
,的中位数可以表示为( )
A. B. C. D.
10.图l是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为、、…、(如表示身高(单位:)在[150,155)内的学生人数).图2是统计
图l中身高在一定范围内学生人数的一个
算法流程图.现要统计身高在
160~180(含160,不含180)
的学生人数,那么在流程图中的判断框
内应填写的条件是( )
A. B.
C. D.
二、填空题:(本大题共5小题,每小题4分,共20分)
11.管理人员从一池塘内捞出30条鱼,做上标记后放回池塘。10天后,又从池塘内捞出50条
鱼,其中有标记的有2条。根据以上数据可以估计该池塘内共有 条鱼。
12.某校高中部有三个年级,其中高三有学生1000人,现采用分层抽样法抽取一个容量为185的样本,已知在高一年级抽取了75人,高二年级抽取了60人,则高中部共有__ __学生。
13 已知辆汽车通过某一段公路时的时速
的频率分布直方图如右图所示,则时速在
的汽车大约有_________辆.
14.已知与之间的一组数据为
0 1 2 3
1 3 5-a 7+a
则与的回归直线方程必过定点______
15. 已知样本的平均数是,标准差是,则
三、解答题
16.在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)
3
4
5
62.5344.5
3 2.5
4 3
5 4
6 4.50
0
0
00000
分组 频数
合计
共有100个数据,将数据分组如右表:
(1)画出频率分布表,并画出频率分布直方图;
(2)估计纤度落在中的概率及纤度小于的概率是
多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
17.在2007全运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用茎叶图表示甲,乙两个成绩;并根据茎叶图分析甲、乙两人成绩;
(2)分别计算两个样本的平均数和标准差s,并根据计算结果估计哪位运动员的成绩比较稳定。
18.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗(吨)标准煤的几组对照数据:
3 4 5 6
2.5 3 4 4.5
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式 ,)
《统计》单元测试参考答案
一、选择题: CABBA, DCCCB
二、填空题:11、750 12、3700 13、80 14、 15、96
三、解答题:
16.(Ⅰ)
分组 频数 频率
4 0.04
25 0.25
30 0.30
29 0.29
10 0.10
2 0.02
合计 100 1.00
(2)纤度落在中的概率约为,
纤度小于1.40的概率约为.
(Ⅲ)总体数据的众数:1.40 中位数:1.408
平均数:
.
17.(1)如图所示,茎表示成绩的整数环数,叶表示小数点后的数字。
由上图知,甲中位数是9.05,乙中位数是9.15,乙的成绩大致对称,
可以看出乙发挥稳定性好,甲波动性大。
(2)解:(3)甲=×(9.4+8.7+7.5+8.4+10.1+10.5+10.7+7.2+7.8+10.8)=9.11
S甲==1.3
乙=×(9.1+8.7+7.1+9.8+9.7+8.5+10.1+9.2+10.1+9.1)=9.14
S乙==0.9
由S甲>S乙,这说明了甲运动员的波动大于乙运动员的波动,所以我们估计,乙运动员比较稳定。
18.(1)散点图如下
(2)
;
所求的回归方程为
(3) 时, (吨)
预测生产100吨甲产品的生产能耗比技改前降低(吨)
