2020-2021学年高二数学人教A版选修2-2第三章3.2.1 复数代数形式的加、减运算及其几何意义 课件(共32张PPT)
文档属性
| 名称 | 2020-2021学年高二数学人教A版选修2-2第三章3.2.1 复数代数形式的加、减运算及其几何意义 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 00:00:00 | ||
图片预览











文档简介
人教A版
选修1-2/2-2
第三章
数系的扩充和复数的引入
3.2.1
复数代数形式的加、减运算及其几何意义
3.2
复数代数形式的四则运算
一
提出问题
1.
引进新数时的设想
设想:实数与新数能像实数那样加法、乘法运算,原有的实数加法、乘法运算律仍成立
虚数
有理数Q
整数Z
自然数N
实数R
负整数
分数
无理数
复数C
2.
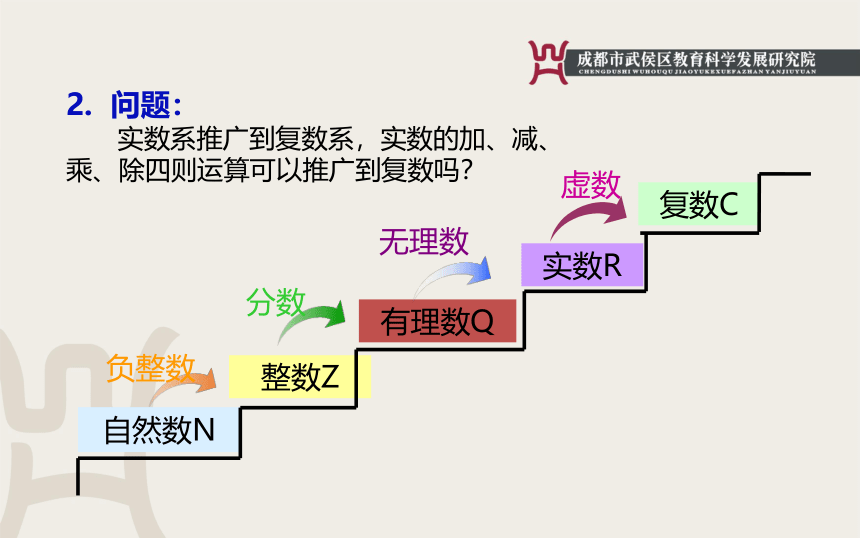
问题:
实数系推广到复数系,实数的加、减、乘、除四则运算可以推广到复数吗?
核心问题:
探究复数代数形式的加、减运算及其几何意义
二
解决问题
1.
复数的加法和运算律
设
,
那么
两个复数的和仍然是一个确定的复数
规定
设
,
,
.
那么
本质是复数的加法和实数加法的交换律
?
?
?
设
,
,
.
那么
本质是复数的加法和实数加法的交换律、结合律
?
?
2.
复数的减法
设
,
那么
类比实数,复数的减法是加法的逆运算
即
两个复数的差仍然是一个确定的复数
则
设
,
,
3.
复数的加法、减法的几何意义
(数)
(形)
一
一对应
复数
平面向量
https://.cn/svg.html#posts/182531
3.
复数的加法、减法的几何意义
复数的加、减法可以按照向量的加、减法进行,这是复数加、减法的几何意义。
三
反思提升
1.
复数的加、减法法则和加法运算律
复数加法交换律
复数加法结合律
2.
复数的加、减法的几何意义
2.
复数的加、减法的几何意义
复数的加、减法可以按照向量的加、减法进行
——这是复数加、减法的几何意义
向量的加、减法有平行四边形法则和三角形法则
3.
方法与思想
待定系数法
设
z=x+yi
数形结合思想
复数的实数化思想
四
运用反馈
1
典型例题
例1 计算
例2 ABCD是复平面内的平行四边形,A,B,C三点对应的复数分别为1+3i,-i,2+i,求向量
对应的复数和
D点对应的复数.
https://.cn/svg.html#posts/182604
例2 ABCD是复平面内的平行四边形,A,B,C三点对应的复数分别为1+3i,-i,2+i,求向量
对应的复数和D点对应的复数。
2
课堂检测
2.若z+3-2i=4+i,则
z
等于(
)
A.1+i
B.1+3i
C.-1-i
D.-1-3i
3.设z1=x+2i,z2=3-yi
(x,y∈R),且
z1+z2=5-6i,
则
z1-z2=__________.
4.
设A为原点,B、C两点对应的复数分别是3+2i和2-4i,
则使得A、B、C、D这四点成平行四边形的点D对应的复数
是
.
√
2.若z+3-2i=4+i,则
z
等于
A.1+i
B.1+3i
C.-1-i
D.-1-3i
√
解析 z=(4+i)-(3-2i)=1+3i.
3.设z1=x+2i,z2=3-yi(x,y∈R),且z1+z2=5-6i,
则z1-z2=__________.
解析 ∵z1+z2=(x+3)+(2-y)i=5-6i,
-1+10i
∴z1-z2=(x-3)+(2+y)i=-1+10i.
4.
设A为原点,B、C两点对应的复数分别是3+2i和2-4i,
则使得A、B、C、D这四点成平行四边形的点D对应的复数是
.
,或
,或
五
课后任务
梳理新学的内容,掌握知识方法,典型例题,选择教材或自选相关题目适当巩固
预习3.2.2
复数代数形式的乘法与除法
本课结束
谢谢!
选修1-2/2-2
第三章
数系的扩充和复数的引入
3.2.1
复数代数形式的加、减运算及其几何意义
3.2
复数代数形式的四则运算
一
提出问题
1.
引进新数时的设想
设想:实数与新数能像实数那样加法、乘法运算,原有的实数加法、乘法运算律仍成立
虚数
有理数Q
整数Z
自然数N
实数R
负整数
分数
无理数
复数C
2.
问题:
实数系推广到复数系,实数的加、减、乘、除四则运算可以推广到复数吗?
核心问题:
探究复数代数形式的加、减运算及其几何意义
二
解决问题
1.
复数的加法和运算律
设
,
那么
两个复数的和仍然是一个确定的复数
规定
设
,
,
.
那么
本质是复数的加法和实数加法的交换律
?
?
?
设
,
,
.
那么
本质是复数的加法和实数加法的交换律、结合律
?
?
2.
复数的减法
设
,
那么
类比实数,复数的减法是加法的逆运算
即
两个复数的差仍然是一个确定的复数
则
设
,
,
3.
复数的加法、减法的几何意义
(数)
(形)
一
一对应
复数
平面向量
https://.cn/svg.html#posts/182531
3.
复数的加法、减法的几何意义
复数的加、减法可以按照向量的加、减法进行,这是复数加、减法的几何意义。
三
反思提升
1.
复数的加、减法法则和加法运算律
复数加法交换律
复数加法结合律
2.
复数的加、减法的几何意义
2.
复数的加、减法的几何意义
复数的加、减法可以按照向量的加、减法进行
——这是复数加、减法的几何意义
向量的加、减法有平行四边形法则和三角形法则
3.
方法与思想
待定系数法
设
z=x+yi
数形结合思想
复数的实数化思想
四
运用反馈
1
典型例题
例1 计算
例2 ABCD是复平面内的平行四边形,A,B,C三点对应的复数分别为1+3i,-i,2+i,求向量
对应的复数和
D点对应的复数.
https://.cn/svg.html#posts/182604
例2 ABCD是复平面内的平行四边形,A,B,C三点对应的复数分别为1+3i,-i,2+i,求向量
对应的复数和D点对应的复数。
2
课堂检测
2.若z+3-2i=4+i,则
z
等于(
)
A.1+i
B.1+3i
C.-1-i
D.-1-3i
3.设z1=x+2i,z2=3-yi
(x,y∈R),且
z1+z2=5-6i,
则
z1-z2=__________.
4.
设A为原点,B、C两点对应的复数分别是3+2i和2-4i,
则使得A、B、C、D这四点成平行四边形的点D对应的复数
是
.
√
2.若z+3-2i=4+i,则
z
等于
A.1+i
B.1+3i
C.-1-i
D.-1-3i
√
解析 z=(4+i)-(3-2i)=1+3i.
3.设z1=x+2i,z2=3-yi(x,y∈R),且z1+z2=5-6i,
则z1-z2=__________.
解析 ∵z1+z2=(x+3)+(2-y)i=5-6i,
-1+10i
∴z1-z2=(x-3)+(2+y)i=-1+10i.
4.
设A为原点,B、C两点对应的复数分别是3+2i和2-4i,
则使得A、B、C、D这四点成平行四边形的点D对应的复数是
.
,或
,或
五
课后任务
梳理新学的内容,掌握知识方法,典型例题,选择教材或自选相关题目适当巩固
预习3.2.2
复数代数形式的乘法与除法
本课结束
谢谢!
