高二数学 选修4-4 坐标系与参数方程 第二讲 参数方程 2.1.1 参数方程的概念及圆的参数方程省录播课 课件(共37张PPT)
文档属性
| 名称 | 高二数学 选修4-4 坐标系与参数方程 第二讲 参数方程 2.1.1 参数方程的概念及圆的参数方程省录播课 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 20:08:09 | ||
图片预览










文档简介
高二数学
选修4-4
坐标系与参数方程
第二讲
参数方程
2.1.1
参数方程的概念及圆的参数方程
一
曲线的参数方程
一
提出问题
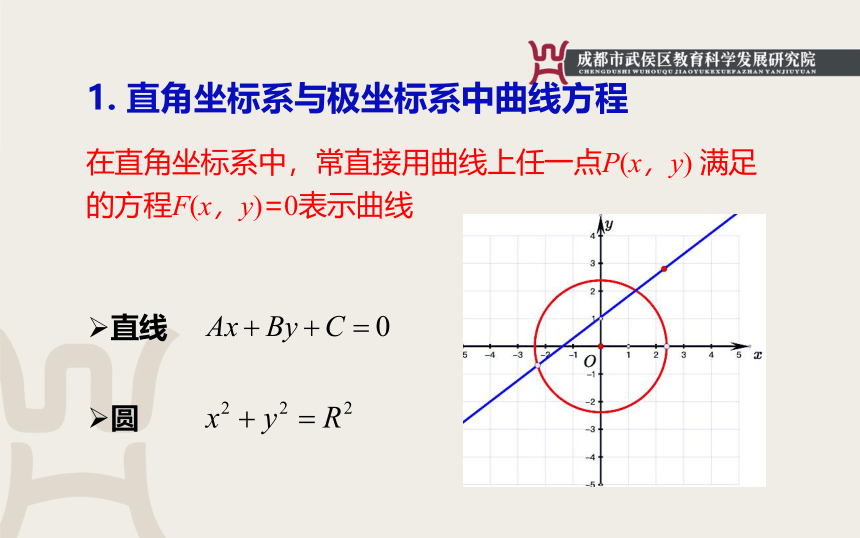
在直角坐标系中,常直接用曲线上任一点P(x,y)
满足
的方程F(x,y)=0表示曲线
1.
直角坐标系与极坐标系中曲线方程
直线
圆
1.
直角坐标系与极坐标系曲线方程
圆锥曲线——椭圆、双曲线、抛物线
在直角坐标系中,常直接用曲线上任一点P(x,y)
满足
的方程F(x,y)=0表示曲线
特殊直线
1.
直角坐标系与极坐标系曲线方程
特殊圆
在极坐标系中,常直接用曲线上任一点
满足的方程
表示曲线
笛卡尔心形曲线
1.
直角坐标系与极坐标系曲线方程
海螺线
在极坐标系中,常直接用曲线上任一点
满足的方程
表示曲线
在直角坐标系中,求某些曲线的方程时,确定P(x,y)中
x,y的方程并不容易,怎么办?
2.
问题
或者说在某些问题中,确定P(x,y)中x,y与另一个量有明显的变化关系?我们可以怎么办?
探究两类常见物理运动中,如何从数学的角度刻画物体在每个时刻的位置?
核心问题
二
解决问题
问题1:
匀速圆周运动
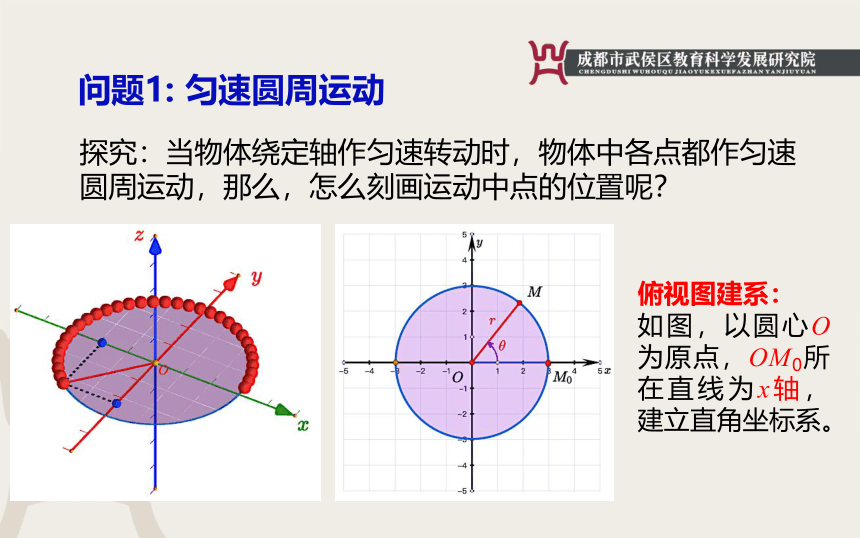
探究:如图,当物体绕定轴作匀速转动时,物体中各点都作匀速圆周运动,那么,怎么刻画运动中点的位置呢?
https://.cn/presentationEditor/presentationPlay.html?page=1#posts/5451
问题1:
匀速圆周运动
探究:当物体绕定轴作匀速转动时,物体中各点都作匀速圆周运动,那么,怎么刻画运动中点的位置呢?
俯视图建系:
如图,以圆心O为原点,OM0所在直线为x轴,建立直角坐标系。
俯视图建系:如图,以圆心O为原点,OM0所在直线为x轴,建立直角坐标系。
设点M转到的角速度是
弧度/秒,则
t
秒转过的角为
弧度
问题1:
匀速圆周运动
方程中
x,y
都用变量
t
或者
表示
当
一定,点
M
的位置由时刻
t
惟一确定,或者由转过的角度
惟一确定.
问题1:
匀速圆周运动
特点:
问题2:
物体平抛运动
如图,一架救援飞机在离灾区地面500
m高处以100
m/s的速度作水平直线飞行
.
为使投放的救援物资准确落于灾区指定的地面(不计空气阻力),飞行员在离救援点的水平距离约多少时投放物资,可以使其准确落在指定地点?
https://.cn/presentationEditor/presentationPlay.html?page=1#posts/5451
问题2:
物体平抛运动
思考:问题中,如何刻画飞机上平抛出去的物体的位置与时间的关系?也就是随时刻物体距离地面的高度和距飞机抛投点的水平距离(或者是距灾区的水平距离)
主视图建系:在经过飞行航线且垂直于地平面的平面上建立如图所示直角坐标系,x
轴为地平面与竖直平面的交线,y
轴经过点A.
探究:物体随时距离地面和距离飞机抛投点的水平距离与时间的关系?
记物体投出机舱时为时刻0,在时刻
t
时物体的位置为点M
(x,y)
,
x表示物体随时的水平距离,y表示物体距地面的高度.
方程中
x,y
都用变量
t
表示
从物理知识的角度,物体的位置由时间惟一确定;
从数学知识的角度,点
M
的坐标(x,y)由
t
惟一确定
特点:
问题:为使投放的救援物资准确落于灾区指定的地面,飞行员在离救援点的水平距离约多少时投放物资,可以使其准确落在指定地点?
令y=0,得t
≈10.10
s
代入x=100t,得
x
≈1010
m.
三
反思提升
1.
参数方程的概念
一般地,在平面直角坐标系中,如果曲线上任意一点的坐标
x,y
都是某个变数
t
的函数
并且对于
t
的每一个允许值,由方程组所确定的点M(x,y)都在这条曲线上,那么方程就叫做这条曲线的参数方程,
联系变数
x,y
的变数
t
叫做参变数,简称参数.
普通方程
2.
参数方程的特点
参数是联系变数x,y的桥梁,可能有物理意义或几何意义,也可以没有明显的实际意义.
参数方程能够明显的揭示物体的运动规律,是描述“运动”
“变化”的有效工具。
参数方程可借助t直接确定曲线上点的位置
普通方程直接得到x,y的对应关系
3.
圆的参数方程
圆心在原点,半径为
R
的圆的参数方程为
圆心在
C(a,b)半径为
R
的圆的参数方程为
4.
方法与思想
运动与变化观
数形结合思想
参数方程思想
参数方程是以变量为中介来表示曲线上的点的坐标的方程,是曲线在同一种坐标系下的又一种形式
.
四
运用反馈
1
典型例题
例1
已知曲线C
的参数方程为
(
t
为参数
),
(1)
判断点
M1(0,1),M2(5,4)与曲线C
的位置关系;
(2)
已知点
M3(6,a)
在曲线C上,求
a
的值.
例2 如图,圆O
的半径为2,P上圆上的动点,Q(6,
0)是
x
轴上的点,M
是
PQ
的中点.
当点
P
绕
O
作匀速圆周运动时,
求点M
的轨迹的参数方程.
例2 如图,圆O
的半径为2,P上圆上的动点,Q(6,
0)是
x
轴上的点,M
是
PQ
的中点.
当点
P
绕
O
作匀速圆周运动时,
求点M
的轨迹的参数方程.
因此,点M的轨迹的参数方程为
解:设点M(x,y),由圆的参数方程知P
又Q(6,
0)
,
M
是
PQ
的中点
由中点坐标公式得
例2 如图,圆O
的半径为2,P上圆上的动点,Q(6,
0)是
x
轴上的点,M
是
PQ
的中点.
当点
P
绕
O
作匀速圆周运动时,
求点M
的轨迹的参数方程.
思考:M
的轨迹是什么?如果点Q在其他位置,轨迹的参数方程与轨迹又是什么?如果M点不是中点,是其他分点呢?
https://.cn/presentationEditor/presentationPlay.html#posts/5452
2
课堂检测
0或2
解析 ∵y=t2=1,∴t=±1.
∴x=1+1=2或x=-1+1=0.
A.
π
B.
2π
C.
3π
D.
4π
√
3.
动点M作匀速直线运动,它在
x
轴和
y
轴方向的速度分别为
3m/s
和
4m/s,直角坐标系的长度单位为1m,点M
的起始位置在点M0(-2,1)处,则点M
的轨迹的参数方程为
.
https://.cn/svg.html#posts/187096
五
课后任务
梳理新学的内容,掌握知识方法,典型例题,选择教材或自选题目适当巩固
预习
选修4-4
2.1.2
参数方程与普通方程的互化
本课结束
谢谢!
选修4-4
坐标系与参数方程
第二讲
参数方程
2.1.1
参数方程的概念及圆的参数方程
一
曲线的参数方程
一
提出问题
在直角坐标系中,常直接用曲线上任一点P(x,y)
满足
的方程F(x,y)=0表示曲线
1.
直角坐标系与极坐标系中曲线方程
直线
圆
1.
直角坐标系与极坐标系曲线方程
圆锥曲线——椭圆、双曲线、抛物线
在直角坐标系中,常直接用曲线上任一点P(x,y)
满足
的方程F(x,y)=0表示曲线
特殊直线
1.
直角坐标系与极坐标系曲线方程
特殊圆
在极坐标系中,常直接用曲线上任一点
满足的方程
表示曲线
笛卡尔心形曲线
1.
直角坐标系与极坐标系曲线方程
海螺线
在极坐标系中,常直接用曲线上任一点
满足的方程
表示曲线
在直角坐标系中,求某些曲线的方程时,确定P(x,y)中
x,y的方程并不容易,怎么办?
2.
问题
或者说在某些问题中,确定P(x,y)中x,y与另一个量有明显的变化关系?我们可以怎么办?
探究两类常见物理运动中,如何从数学的角度刻画物体在每个时刻的位置?
核心问题
二
解决问题
问题1:
匀速圆周运动
探究:如图,当物体绕定轴作匀速转动时,物体中各点都作匀速圆周运动,那么,怎么刻画运动中点的位置呢?
https://.cn/presentationEditor/presentationPlay.html?page=1#posts/5451
问题1:
匀速圆周运动
探究:当物体绕定轴作匀速转动时,物体中各点都作匀速圆周运动,那么,怎么刻画运动中点的位置呢?
俯视图建系:
如图,以圆心O为原点,OM0所在直线为x轴,建立直角坐标系。
俯视图建系:如图,以圆心O为原点,OM0所在直线为x轴,建立直角坐标系。
设点M转到的角速度是
弧度/秒,则
t
秒转过的角为
弧度
问题1:
匀速圆周运动
方程中
x,y
都用变量
t
或者
表示
当
一定,点
M
的位置由时刻
t
惟一确定,或者由转过的角度
惟一确定.
问题1:
匀速圆周运动
特点:
问题2:
物体平抛运动
如图,一架救援飞机在离灾区地面500
m高处以100
m/s的速度作水平直线飞行
.
为使投放的救援物资准确落于灾区指定的地面(不计空气阻力),飞行员在离救援点的水平距离约多少时投放物资,可以使其准确落在指定地点?
https://.cn/presentationEditor/presentationPlay.html?page=1#posts/5451
问题2:
物体平抛运动
思考:问题中,如何刻画飞机上平抛出去的物体的位置与时间的关系?也就是随时刻物体距离地面的高度和距飞机抛投点的水平距离(或者是距灾区的水平距离)
主视图建系:在经过飞行航线且垂直于地平面的平面上建立如图所示直角坐标系,x
轴为地平面与竖直平面的交线,y
轴经过点A.
探究:物体随时距离地面和距离飞机抛投点的水平距离与时间的关系?
记物体投出机舱时为时刻0,在时刻
t
时物体的位置为点M
(x,y)
,
x表示物体随时的水平距离,y表示物体距地面的高度.
方程中
x,y
都用变量
t
表示
从物理知识的角度,物体的位置由时间惟一确定;
从数学知识的角度,点
M
的坐标(x,y)由
t
惟一确定
特点:
问题:为使投放的救援物资准确落于灾区指定的地面,飞行员在离救援点的水平距离约多少时投放物资,可以使其准确落在指定地点?
令y=0,得t
≈10.10
s
代入x=100t,得
x
≈1010
m.
三
反思提升
1.
参数方程的概念
一般地,在平面直角坐标系中,如果曲线上任意一点的坐标
x,y
都是某个变数
t
的函数
并且对于
t
的每一个允许值,由方程组所确定的点M(x,y)都在这条曲线上,那么方程就叫做这条曲线的参数方程,
联系变数
x,y
的变数
t
叫做参变数,简称参数.
普通方程
2.
参数方程的特点
参数是联系变数x,y的桥梁,可能有物理意义或几何意义,也可以没有明显的实际意义.
参数方程能够明显的揭示物体的运动规律,是描述“运动”
“变化”的有效工具。
参数方程可借助t直接确定曲线上点的位置
普通方程直接得到x,y的对应关系
3.
圆的参数方程
圆心在原点,半径为
R
的圆的参数方程为
圆心在
C(a,b)半径为
R
的圆的参数方程为
4.
方法与思想
运动与变化观
数形结合思想
参数方程思想
参数方程是以变量为中介来表示曲线上的点的坐标的方程,是曲线在同一种坐标系下的又一种形式
.
四
运用反馈
1
典型例题
例1
已知曲线C
的参数方程为
(
t
为参数
),
(1)
判断点
M1(0,1),M2(5,4)与曲线C
的位置关系;
(2)
已知点
M3(6,a)
在曲线C上,求
a
的值.
例2 如图,圆O
的半径为2,P上圆上的动点,Q(6,
0)是
x
轴上的点,M
是
PQ
的中点.
当点
P
绕
O
作匀速圆周运动时,
求点M
的轨迹的参数方程.
例2 如图,圆O
的半径为2,P上圆上的动点,Q(6,
0)是
x
轴上的点,M
是
PQ
的中点.
当点
P
绕
O
作匀速圆周运动时,
求点M
的轨迹的参数方程.
因此,点M的轨迹的参数方程为
解:设点M(x,y),由圆的参数方程知P
又Q(6,
0)
,
M
是
PQ
的中点
由中点坐标公式得
例2 如图,圆O
的半径为2,P上圆上的动点,Q(6,
0)是
x
轴上的点,M
是
PQ
的中点.
当点
P
绕
O
作匀速圆周运动时,
求点M
的轨迹的参数方程.
思考:M
的轨迹是什么?如果点Q在其他位置,轨迹的参数方程与轨迹又是什么?如果M点不是中点,是其他分点呢?
https://.cn/presentationEditor/presentationPlay.html#posts/5452
2
课堂检测
0或2
解析 ∵y=t2=1,∴t=±1.
∴x=1+1=2或x=-1+1=0.
A.
π
B.
2π
C.
3π
D.
4π
√
3.
动点M作匀速直线运动,它在
x
轴和
y
轴方向的速度分别为
3m/s
和
4m/s,直角坐标系的长度单位为1m,点M
的起始位置在点M0(-2,1)处,则点M
的轨迹的参数方程为
.
https://.cn/svg.html#posts/187096
五
课后任务
梳理新学的内容,掌握知识方法,典型例题,选择教材或自选题目适当巩固
预习
选修4-4
2.1.2
参数方程与普通方程的互化
本课结束
谢谢!
