高二数学选修4-4 坐标系与参数方程 第二讲参数方程 2.1.2 参数方程与普通方程的互化省录播课 课件(共25张PPT)
文档属性
| 名称 | 高二数学选修4-4 坐标系与参数方程 第二讲参数方程 2.1.2 参数方程与普通方程的互化省录播课 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 00:00:00 | ||
图片预览







文档简介
选修4-4
坐标系与参数方程
第二讲
参数方程
2.1.2
参数方程与普通方程的互化
一
曲线的参数方程
一
提出问题
参数方程与普通方程各有其特点和优越性
参数方程与普通方程有怎样的联系?可以怎样相互转化呢?
参数方程是以参数t为中介、桥梁,借助t直接确定曲线上点的位置
普通方程直接得到x,y的对应关系,再确定点的位置
?
探究曲线的参数方程与普通方程的互化
核心问题
二
解决问题
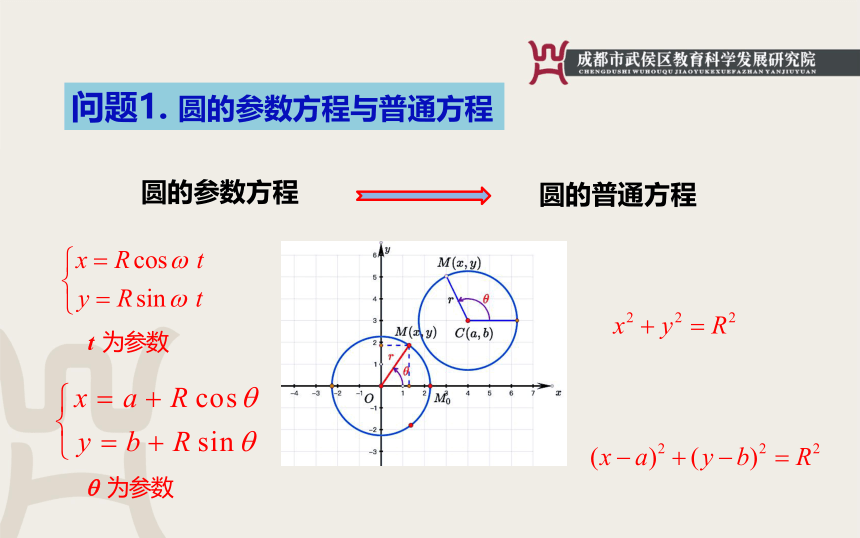
问题1.
圆的参数方程与普通方程
圆的参数方程
圆的普通方程
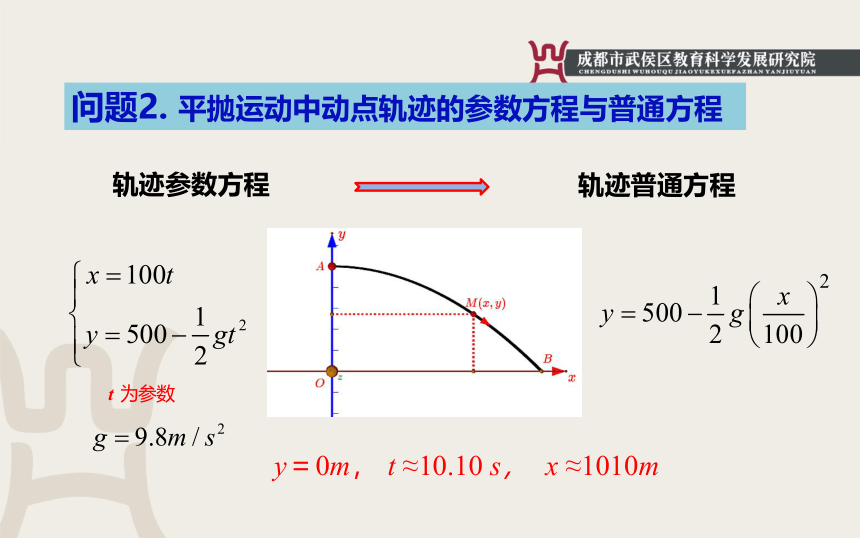
问题2.
平抛运动中动点轨迹的参数方程与普通方程
轨迹参数方程
轨迹普通方程
y=0m,
t
≈10.10
s,
x
≈1010m
问题3.
普通方程如何化为参数方程?
椭圆的普通方程
思路
椭圆的参数方程
问题3.
普通方程如何化为参数方程?
思路二
https://.cn/presentationEditor/presentationPlay.html#posts/5453
问题3.
普通方程如何化为参数方程?
思路二
右半椭圆
左半椭圆
问题3.
普通方程如何化为参数方程?
思路一
思路二
和
椭圆的普通方程
椭圆的参数方程
三
反思提升
1.
参数方程与普通方程互化
消参
x,y
的取值范围要一致
消参的方法
代入消参法
三角恒等变换
恒等变形整体代换
参数方程有时不易看出曲线类型,通过曲线的普通方程来判断曲线的类型.
引参
参数可以有一定物理、几何意义,也可以
无明显的实际意义
引进恰当的参数,寻求曲线上任一点M的坐标
x,y
和参数的关系,有利于处理曲线上任一点的相关问题.
1.
参数方程与普通方程互化
消参
参数方程与普通方程互化,很容易改变了变量的取值范围,要注意参数方程与普通方程的等价性.
引参
1.
参数方程与普通方程互化
消参
参数方程思想
引参
2.
方法与思想
等价转化思想
四
运用反馈
1
典型例题
例1 将下列参数方程化为普通方程
例2 将下列普通方程化为普通方程
2
课堂检测
五
课后任务
梳理新学的内容,掌握知识方法,典型例题,选择教材或自选相关题目适当巩固
预习
2.2.1
圆锥曲线(椭圆)的参数方程
本课结束
谢谢!
坐标系与参数方程
第二讲
参数方程
2.1.2
参数方程与普通方程的互化
一
曲线的参数方程
一
提出问题
参数方程与普通方程各有其特点和优越性
参数方程与普通方程有怎样的联系?可以怎样相互转化呢?
参数方程是以参数t为中介、桥梁,借助t直接确定曲线上点的位置
普通方程直接得到x,y的对应关系,再确定点的位置
?
探究曲线的参数方程与普通方程的互化
核心问题
二
解决问题
问题1.
圆的参数方程与普通方程
圆的参数方程
圆的普通方程
问题2.
平抛运动中动点轨迹的参数方程与普通方程
轨迹参数方程
轨迹普通方程
y=0m,
t
≈10.10
s,
x
≈1010m
问题3.
普通方程如何化为参数方程?
椭圆的普通方程
思路
椭圆的参数方程
问题3.
普通方程如何化为参数方程?
思路二
https://.cn/presentationEditor/presentationPlay.html#posts/5453
问题3.
普通方程如何化为参数方程?
思路二
右半椭圆
左半椭圆
问题3.
普通方程如何化为参数方程?
思路一
思路二
和
椭圆的普通方程
椭圆的参数方程
三
反思提升
1.
参数方程与普通方程互化
消参
x,y
的取值范围要一致
消参的方法
代入消参法
三角恒等变换
恒等变形整体代换
参数方程有时不易看出曲线类型,通过曲线的普通方程来判断曲线的类型.
引参
参数可以有一定物理、几何意义,也可以
无明显的实际意义
引进恰当的参数,寻求曲线上任一点M的坐标
x,y
和参数的关系,有利于处理曲线上任一点的相关问题.
1.
参数方程与普通方程互化
消参
参数方程与普通方程互化,很容易改变了变量的取值范围,要注意参数方程与普通方程的等价性.
引参
1.
参数方程与普通方程互化
消参
参数方程思想
引参
2.
方法与思想
等价转化思想
四
运用反馈
1
典型例题
例1 将下列参数方程化为普通方程
例2 将下列普通方程化为普通方程
2
课堂检测
五
课后任务
梳理新学的内容,掌握知识方法,典型例题,选择教材或自选相关题目适当巩固
预习
2.2.1
圆锥曲线(椭圆)的参数方程
本课结束
谢谢!
