人教A版 选修1-22-2 第三章 数系的扩充和复数的引入 3.1.2 复数的几何意义 省录播课 课件(共41张PPT)
文档属性
| 名称 | 人教A版 选修1-22-2 第三章 数系的扩充和复数的引入 3.1.2 复数的几何意义 省录播课 课件(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-05 20:14:57 | ||
图片预览









文档简介
人教A版
选修1-2/2-2
第三章
数系的扩充和复数的引入
3.1.2
复数的几何意义
3.1
数系的扩充和复数的引入
一
提出问题
实部
虚部
复数与数系的扩充
虚数
有理数Q
整数Z
自然数N
实数R
负整数
分数
无理数
复数C
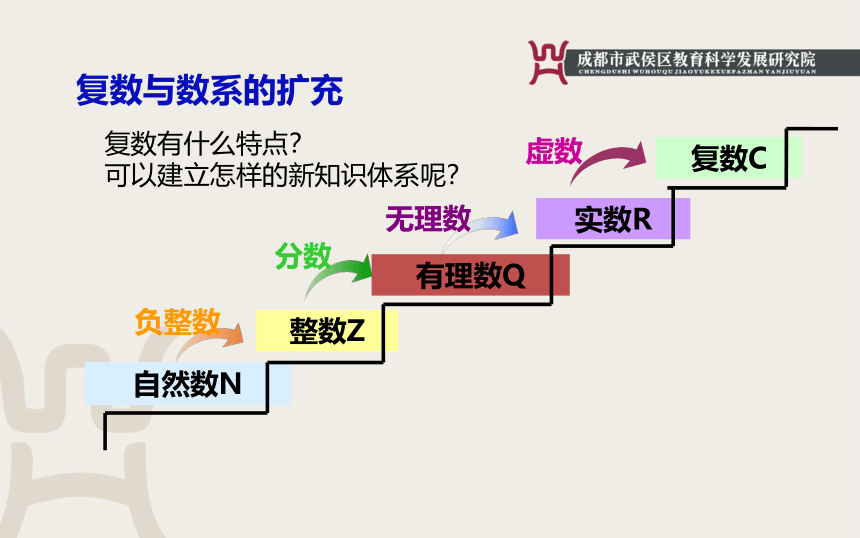
复数与数系的扩充
复数有什么特点?
可以建立怎样的新知识体系呢?
(1)实数有什么性质和特点?能否全部推广到复数集?
实数可以判定相等,不相等,比较大小;
实数的几何意义是任意实数都可以用数轴上的点表示;
实数可以进行四则运算;
实数的乘方、负实数不能进行开偶次方根运算;
实数范围内有解方程、不等式与函数性质;
……
问题:
(1)
实数有什么性质和特点?能否全部推广到复数集?
(2)
从复数的概念出发,复数集有怎样的性质和特点?
复数只有相等或不相等,不能比较大小.
复数有几何意义吗?几何意义是什么?
复数可以怎样进行四则运算?
……
问题:
核心问题:探究复数的几何意义
实数可以判定相等,不相等,比较大小;
实数的几何意义是任意实数都可以用数轴上的点表示;
实数可以进行四则运算;
实数的乘方、负实数不能进行开偶次方根运算;
实数范围内有解方程、不等式与函数性质
……
复数只有相等或不相等,不能比较大小
复数可以怎样进行四则运算?
复数有几何意义吗?几何意义是什么?
复数有等式,没有不等式
……
二
解决问题
实数可以用数轴上的点来表示
x
0
1
一
一对应
实数
数轴上的点
(形)
(数)
实数的几何模型:
A
1.
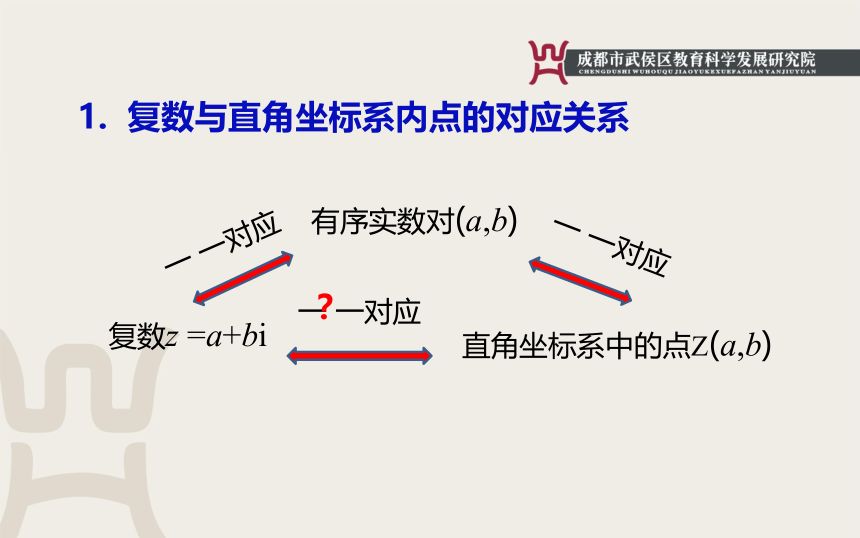
复数与直角坐标系内点的对应关系
复数z
=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
一
一对应
一
一对应
一
一对应
?
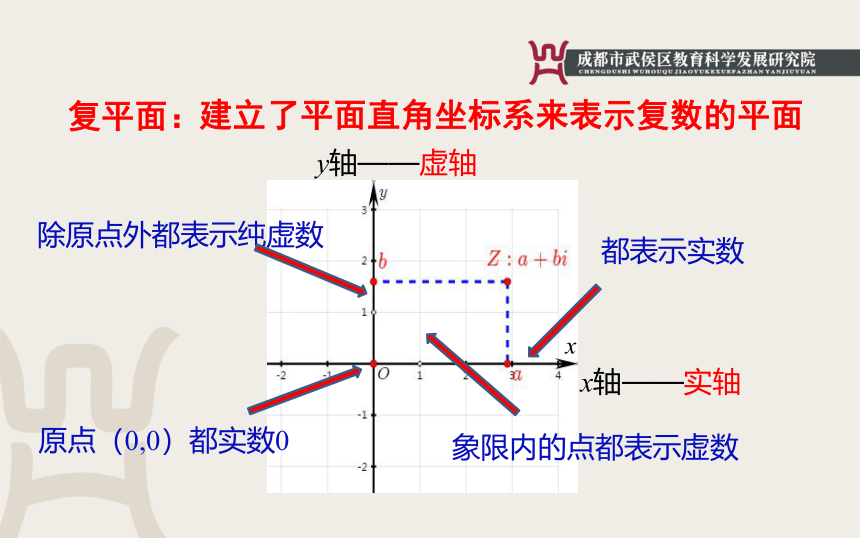
复平面:
y轴——虚轴
象限内的点都表示虚数
除原点外都表示纯虚数
都表示实数
原点(0,0)都实数0
建立了平面直角坐标系来表示复数的平面
x轴——实轴
复数的这种几何表示是1797年有挪威的测量学家韦塞尔(Caspar
Wessel
)提出来的,得到数学家高斯认同。
复数集C与复平面内所有的点构成的集合集是一一对应
——这就是复数的一种几何意义
复数z
=a+bi
(数)
(形)
一
一对应
复平面内的点Z(a,b)
https://.cn/svg.html#posts/182528
2.
复数与平面向量的对应关系
一
一对应
一
一对应
?
复数z
=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
(数)
(形)
一
一对应
一
一对应
一
一对应
平面向量
(形)
https://.cn/svg.html#posts/182528
2.
复数与平面向量的对应关系
(数)
(形)
一
一对应
复数集C与复平面内的向量所成的集合也是一
一对应
——这就是复数的另一种几何意义。
复数
平面向量
规定:相等的向量表示同一个复数.
思考:
所对应的复数是什么呢?
三
反思提升
1
.
复数的几何意义
复数集C与复平面内所有的点构成的集合是一
一对应
(数)
(形)
一
一对应
一
一对应
复数集C与复平面内的向量所成的集合也是一
一对应
复数
平面向量
复平面内的点Z(a,b)
数形结合思想
复数
(a,b∈R)可以用向量
表示向量
的模叫做复数
z
的
模,记作|z|或|a+bi|
2
.
复数的模
复数问题实数化思想
实数绝对值的几何意义
复数模其实是实数绝对值的推广
x
O
A
a
|a|
=
|OA|
实数a在数轴上所对应的点A到原点O的距离.
复数模的几何意义
复数
z=a+bi在复平面上对应的点
Z(a,b)
到原点的距离.
x
O
z=a+bi
y
Z(a,b)
3.
思考:
若|z|=r,则复数
z
对应复平面内的点的轨迹是什么?
若|z|呢?
https://.cn/svg.html#posts/182606
若|z|=r,则复数
z
对应复平面内的点到原点的距离为定值r,即是以原点为圆心,半径为r
的圆.
若|z|z
对应复平面内的点的轨迹是以原点为圆心,半径为
r
的圆面(不包括边界).
四
运用反馈
1
典型例题
例1
说出图中复平面内各点所表示的复数和在复平面内描出下列各复数的点。
例2
实数
m
取什么值时,复平面内表示复数
的点
(1)位于第四象限;
(2)位于直线
y=x
上;(3)位于第一、三象限.
即
解:
(1)由
知
(2)由题知:
即
解:
(3)由
表示的点位于第一、三象限知:
即
(2)
已知复数z=3+ai,且
|z|<4,求实数
a
的取值范围.
例3
(1)
若复数z=(a+2)-2ai
的模等于
,求实数a
的值.
例3
(1)
若复数z=(a+2)-2ai
的模等于
,求实数a
的值.
(2)已知复数
z=3+ai,且
|z|<4,求实数a的取值范围.
例3
解 方法一 ∵z=3+ai
(a∈R),
由已知得
32+a2<42,
(2)
已知复数z=3+ai,且
|z|<4,求实数a的取值范围.
例3
方法二 由|z|<4知,z在复平面内对应的点在以原点为圆心,以4为半径的圆内(不包括边界).
由z=3+ai知z对应的点在直线x=3上,所以线段AB(除去端点)为动点Z的集合.
2
课堂检测
1.
在复平面内,复数
z=i-2
对应的点位于(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.
当
(i为虚数单位)在复平面内对应的点位于(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.
若复数z=(m-2)+(m+1)
i
为纯虚数
(i为虚数单位),
其中m∈R,则|z|=_____.
4.
在复平面内表示复数z=(m-3)+2
i
的点在直线
y=x上,
则实数m的值为_____.
1.
在复平面内,复数
z=i-2
对应的点位于
A.第一象限
B.第二象限
C.第三象限
D.第四象限
解析 z=i-2=-2+
i
对应的点为
(-2,1)
在第二象限.
√
2.
当
(i为虚数单位)在复平面内对应的点位于(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
√
∴0<3m-2<1,
m-1<
0
∴
复数
z
在复平面内对应的点位于第四象限.
3.
若复数
z=(m-2)+(m+1)
i
为纯虚数(i为虚数单位),
其中m∈R,则
|z|=_____.
解析 复数z=(m-2)+(m+1)i
为纯虚数(i为虚数单位),
所以m-2=0且m+1≠0,解得m=2,
所以z=3i,所以|z|=3.
3
4.
在复平面内表示复数z=(m-3)+2
i
的点在
直线
y=x
上,则实数m的值为_____.
9
五
课后任务
梳理新学《3.1.2复数的几何意义》,掌握知识方法,典型例题,选择教材或自选相关题目适当巩固
预习3.2.1
复数代数形式的加、减运算及其几何意义
本课结束
谢谢!
选修1-2/2-2
第三章
数系的扩充和复数的引入
3.1.2
复数的几何意义
3.1
数系的扩充和复数的引入
一
提出问题
实部
虚部
复数与数系的扩充
虚数
有理数Q
整数Z
自然数N
实数R
负整数
分数
无理数
复数C
复数与数系的扩充
复数有什么特点?
可以建立怎样的新知识体系呢?
(1)实数有什么性质和特点?能否全部推广到复数集?
实数可以判定相等,不相等,比较大小;
实数的几何意义是任意实数都可以用数轴上的点表示;
实数可以进行四则运算;
实数的乘方、负实数不能进行开偶次方根运算;
实数范围内有解方程、不等式与函数性质;
……
问题:
(1)
实数有什么性质和特点?能否全部推广到复数集?
(2)
从复数的概念出发,复数集有怎样的性质和特点?
复数只有相等或不相等,不能比较大小.
复数有几何意义吗?几何意义是什么?
复数可以怎样进行四则运算?
……
问题:
核心问题:探究复数的几何意义
实数可以判定相等,不相等,比较大小;
实数的几何意义是任意实数都可以用数轴上的点表示;
实数可以进行四则运算;
实数的乘方、负实数不能进行开偶次方根运算;
实数范围内有解方程、不等式与函数性质
……
复数只有相等或不相等,不能比较大小
复数可以怎样进行四则运算?
复数有几何意义吗?几何意义是什么?
复数有等式,没有不等式
……
二
解决问题
实数可以用数轴上的点来表示
x
0
1
一
一对应
实数
数轴上的点
(形)
(数)
实数的几何模型:
A
1.
复数与直角坐标系内点的对应关系
复数z
=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
一
一对应
一
一对应
一
一对应
?
复平面:
y轴——虚轴
象限内的点都表示虚数
除原点外都表示纯虚数
都表示实数
原点(0,0)都实数0
建立了平面直角坐标系来表示复数的平面
x轴——实轴
复数的这种几何表示是1797年有挪威的测量学家韦塞尔(Caspar
Wessel
)提出来的,得到数学家高斯认同。
复数集C与复平面内所有的点构成的集合集是一一对应
——这就是复数的一种几何意义
复数z
=a+bi
(数)
(形)
一
一对应
复平面内的点Z(a,b)
https://.cn/svg.html#posts/182528
2.
复数与平面向量的对应关系
一
一对应
一
一对应
?
复数z
=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
(数)
(形)
一
一对应
一
一对应
一
一对应
平面向量
(形)
https://.cn/svg.html#posts/182528
2.
复数与平面向量的对应关系
(数)
(形)
一
一对应
复数集C与复平面内的向量所成的集合也是一
一对应
——这就是复数的另一种几何意义。
复数
平面向量
规定:相等的向量表示同一个复数.
思考:
所对应的复数是什么呢?
三
反思提升
1
.
复数的几何意义
复数集C与复平面内所有的点构成的集合是一
一对应
(数)
(形)
一
一对应
一
一对应
复数集C与复平面内的向量所成的集合也是一
一对应
复数
平面向量
复平面内的点Z(a,b)
数形结合思想
复数
(a,b∈R)可以用向量
表示向量
的模叫做复数
z
的
模,记作|z|或|a+bi|
2
.
复数的模
复数问题实数化思想
实数绝对值的几何意义
复数模其实是实数绝对值的推广
x
O
A
a
|a|
=
|OA|
实数a在数轴上所对应的点A到原点O的距离.
复数模的几何意义
复数
z=a+bi在复平面上对应的点
Z(a,b)
到原点的距离.
x
O
z=a+bi
y
Z(a,b)
3.
思考:
若|z|=r,则复数
z
对应复平面内的点的轨迹是什么?
若|z|
https://.cn/svg.html#posts/182606
若|z|=r,则复数
z
对应复平面内的点到原点的距离为定值r,即是以原点为圆心,半径为r
的圆.
若|z|
对应复平面内的点的轨迹是以原点为圆心,半径为
r
的圆面(不包括边界).
四
运用反馈
1
典型例题
例1
说出图中复平面内各点所表示的复数和在复平面内描出下列各复数的点。
例2
实数
m
取什么值时,复平面内表示复数
的点
(1)位于第四象限;
(2)位于直线
y=x
上;(3)位于第一、三象限.
即
解:
(1)由
知
(2)由题知:
即
解:
(3)由
表示的点位于第一、三象限知:
即
(2)
已知复数z=3+ai,且
|z|<4,求实数
a
的取值范围.
例3
(1)
若复数z=(a+2)-2ai
的模等于
,求实数a
的值.
例3
(1)
若复数z=(a+2)-2ai
的模等于
,求实数a
的值.
(2)已知复数
z=3+ai,且
|z|<4,求实数a的取值范围.
例3
解 方法一 ∵z=3+ai
(a∈R),
由已知得
32+a2<42,
(2)
已知复数z=3+ai,且
|z|<4,求实数a的取值范围.
例3
方法二 由|z|<4知,z在复平面内对应的点在以原点为圆心,以4为半径的圆内(不包括边界).
由z=3+ai知z对应的点在直线x=3上,所以线段AB(除去端点)为动点Z的集合.
2
课堂检测
1.
在复平面内,复数
z=i-2
对应的点位于(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.
当
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.
若复数z=(m-2)+(m+1)
i
为纯虚数
(i为虚数单位),
其中m∈R,则|z|=_____.
4.
在复平面内表示复数z=(m-3)+2
i
的点在直线
y=x上,
则实数m的值为_____.
1.
在复平面内,复数
z=i-2
对应的点位于
A.第一象限
B.第二象限
C.第三象限
D.第四象限
解析 z=i-2=-2+
i
对应的点为
(-2,1)
在第二象限.
√
2.
当
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
√
∴0<3m-2<1,
m-1<
0
∴
复数
z
在复平面内对应的点位于第四象限.
3.
若复数
z=(m-2)+(m+1)
i
为纯虚数(i为虚数单位),
其中m∈R,则
|z|=_____.
解析 复数z=(m-2)+(m+1)i
为纯虚数(i为虚数单位),
所以m-2=0且m+1≠0,解得m=2,
所以z=3i,所以|z|=3.
3
4.
在复平面内表示复数z=(m-3)+2
i
的点在
直线
y=x
上,则实数m的值为_____.
9
五
课后任务
梳理新学《3.1.2复数的几何意义》,掌握知识方法,典型例题,选择教材或自选相关题目适当巩固
预习3.2.1
复数代数形式的加、减运算及其几何意义
本课结束
谢谢!
